岩石压缩能量演化规律及非线性演化模型研究

张 佳

(辽宁铁道职业技术学院 铁道工程学院，辽宁 锦州 121000)

0 引 言

随着巷道开挖深度不断增加，对于开挖工程安全性的要求也越来越高，故需要准确掌握围岩变形破坏机理，以确保煤炭资源开采的安全性。近些年，以能量角度来分析岩石的变形破坏过程越来越受到认可。国内外学者对不同地质条件下围岩的变形破坏规律和岩石压缩能量演化规律之间的联系展开了深入研究，并取得了丰硕的成果[1-3]，其中通过岩石整个变形破坏过程中能量演化和损伤演化，来分析岩石的破坏机制的方法尤其受到重视[4-6]。大多数关于岩石能量演化特性的研究都是基于单轴或者三轴压缩试验数据和现有能量计算公式，来研究能量演化与损伤破坏的关系，对能量与变形之间物理模型的研究则相对较少。

高速等[7]对大理岩开展峰前、峰后卸围压试验研究，分析了岩石破坏特征及能量耗散规律，得出在卸载破坏过程中，弹性应变能释放速度和能量耗散速率随卸载速率增大而增大。温韬等[8]分析砂岩在不同卸载条件下的能量变化情况，得出能量的耗散会导致岩石产生损伤；且卸围压使岩样束缚减小，加速了损伤的发展，岩样所受的应力状态趋不平衡。为探寻加载过程中节理岩体压缩能量演化规律，基于单轴压缩试验结果及岩石能量原理，王桂林等[9]研究非贯通节理岩体变形破坏过程中总能量、弹性应变能及耗散能的转化特征，揭示了节理岩体损伤破坏的能量演化机制。宋洪强等[10]为了更加有效地评价岩石的脆性，基于能量跌落系数和峰前总能量中可释放弹性能占比，结合岩石破坏全过程的应力-应变曲线，提出一种改进的能量跌落系数模型。ZHOU等[11]认为岩石加载变形变化规律与能量演化规律有关，对砂岩开展了三轴循环加载力学特性试验，在试验数据的基础上提出了弹性能量转换率和弹性能量转换函数理论，探讨了岩石在三轴循环加载条件下的能量演化规律。YAN等[12]发现了岩石的变形特性和能量演化规律受横向尺度效应的影响，故采用PFC2D离散元软件，模拟了不同纵横比岩石的加载破坏情况，并分析了纵横比对能量演化特征的影响程度。ZHAO等[13]认为现有传统的屈服准则无法较好地描述岩石强度特性，故在大量岩石力学特性试验的基础上，总结了岩石在变形破坏过程中的能量转换特征，进而基于能量积聚与释放之间的关系，建立岩石能量强度准则。

上述研究中只是对岩石在不同应力路径下岩石压缩能量演化规律的描述，探讨了耗散机制下岩石破坏机理，部分研究中建立的能量模型仅涉及弹性能曲线峰前阶段的变化规律，未能对弹性能曲线峰后变形阶段的弹性能-应变变化规律进行描述，且建立的模型大多是抽象的经验模型，缺少对能量模型应用的验证；同时，以岩石的能量演化特征研究岩体破坏机制问题以及构建相应的能量本构模型，是揭示岩石破坏的能量演化机制的主要途径之一，也是当下岩石力学研究领域的热点之一。因此，需要结合岩石在变形破坏过程的能量积聚演化特征，构建岩石破坏过程的能量非线性演化模型，进而给出岩石破坏的能量预测判据。

笔者通过对阜新恒大煤矿的砂岩进行常规三轴压缩试验，分析砂岩在不同围压作用下的变形特性，以及能量演化和变形破坏机理之间的关系；通过能量释放率理论、等效应变假设原理和广义胡克定律，构建一种能量非线性演化模型，来预测在加载过程中弹性能随着应变的演化规律，并结合试验数据对模型曲线进行对比验证；同时，建立的模型也需对能量曲线峰后阶段有较好的描述。

1 砂岩三轴压缩试验

1.1 试验方案

笔者采用辽宁工程技术大学矿业学院MTS815.02岩石三轴试验机，对砂岩进行室内三轴压缩试验，用于试验的岩样均采自恒大煤矿；所选取的砂岩试样埋深达800～850 m，岩样外观呈暗灰色，结构相对均匀、质地比较坚硬，不存在肉眼可见的微裂隙和层理。为减小试样的差异性，确保试验的可对比性，挑选的岩块均采自同一断面。经实验室加工成高度100 mm、直径50 mm的标准圆柱形试件(三轴压缩试验为假三轴试验，施加的应力满足以下关系：σ1>σ2=σ3，其中σ1为轴向应力，σ2和σ3为径向应力)。然后，按照水利水电工程岩石试验规程对砂岩进行密度试验、含水率试验和岩石自然吸水率试验；通过烘干法试验测得砂岩的含水率为0.171%，通过自由吸水法试验测定出砂岩的自然吸水率为2.349%，通过量积法试验测试出砂岩的密度为2.355 g/cm3。

试验方案如下：①以500 N/s的加载速率施加一个较小的轴向应力，使得使试件和压头密切接触；②以500 N/s的加载速率按静水压力条件将围压加载至预定值，围压分别选取0、10、20、30、40 MPa(由于所取岩石随处趋于的地应力较高，经过实测得到其水平地应力最大值达到45 MPa，垂直地应力为25 MPa，故该区域属于高地应力环境)，并保持围压在试验过程中不变；③设计相应位移上限值(轴向采用位移加载控制)，加载速率为0.002 mm/s、直至岩样破坏；④待施加的应力达到峰值应力时，继续保持围压不变，以同样的速率施加轴向应变，直至岩样测得残余应力-应变关系后，逐渐卸载轴压与围压直至零，并将试验数据保存并导出；⑤停止数据采集，先卸轴压然后卸围压，取出试件；⑥在数据采集系统中导出试验数据，并保存。

为保证常规三轴压缩试验在每一种围压作用下的应力-应变曲线正确性，每一组围压条件下选取3个试样进行试验，然后取平均值。

1.2 试验结果分析

在不同围压作用下的应力-应变曲线如图1所示。

图1 应力-应变曲线

由图1可知，在压密阶段，岩石内部原有孔隙在外荷载作用下开始闭合，此时曲线基本重合、没有明显的偏离；进入弹性阶段后，由于围压的增大使得应变受到束缚程度加剧，导致随着偏应力的增大，轴向应变虽然继续增大，但曲线开始出现明显的偏离；岩石在塑性阶段时，随着围压继续增大曲线偏离程度越大，且岩石峰值点所对应的应力也越大；在进入峰后软化阶段后，随着应变的逐步增大、应力开始迅速下降逐渐趋于平稳。相对于单轴压缩，常规三轴加荷破坏的峰值强度、峰值应变以及残余强度都显著提高。

根据图1的应力-应变曲线数据，总结出三轴压缩试验结果见表1。

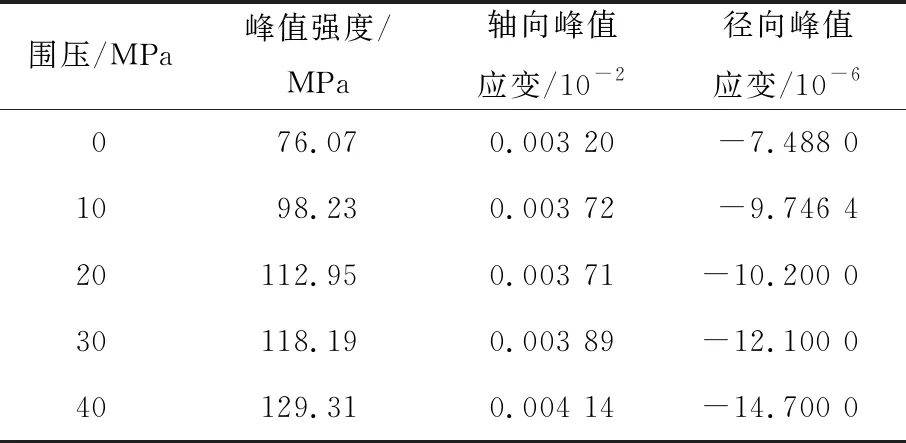
表1 岩石力学特性试验结果

一般采用莫尔应力圆理论来确定岩石的强度参数。假设中间主应力对岩石强度参数不影响，且包络线与正应力的夹角为内摩擦角，与剪切应力轴的截距为黏聚力。根据表1中岩石在不同围压作用下的峰值强度，绘制出围压与峰值强度的关系曲线如图2所示。

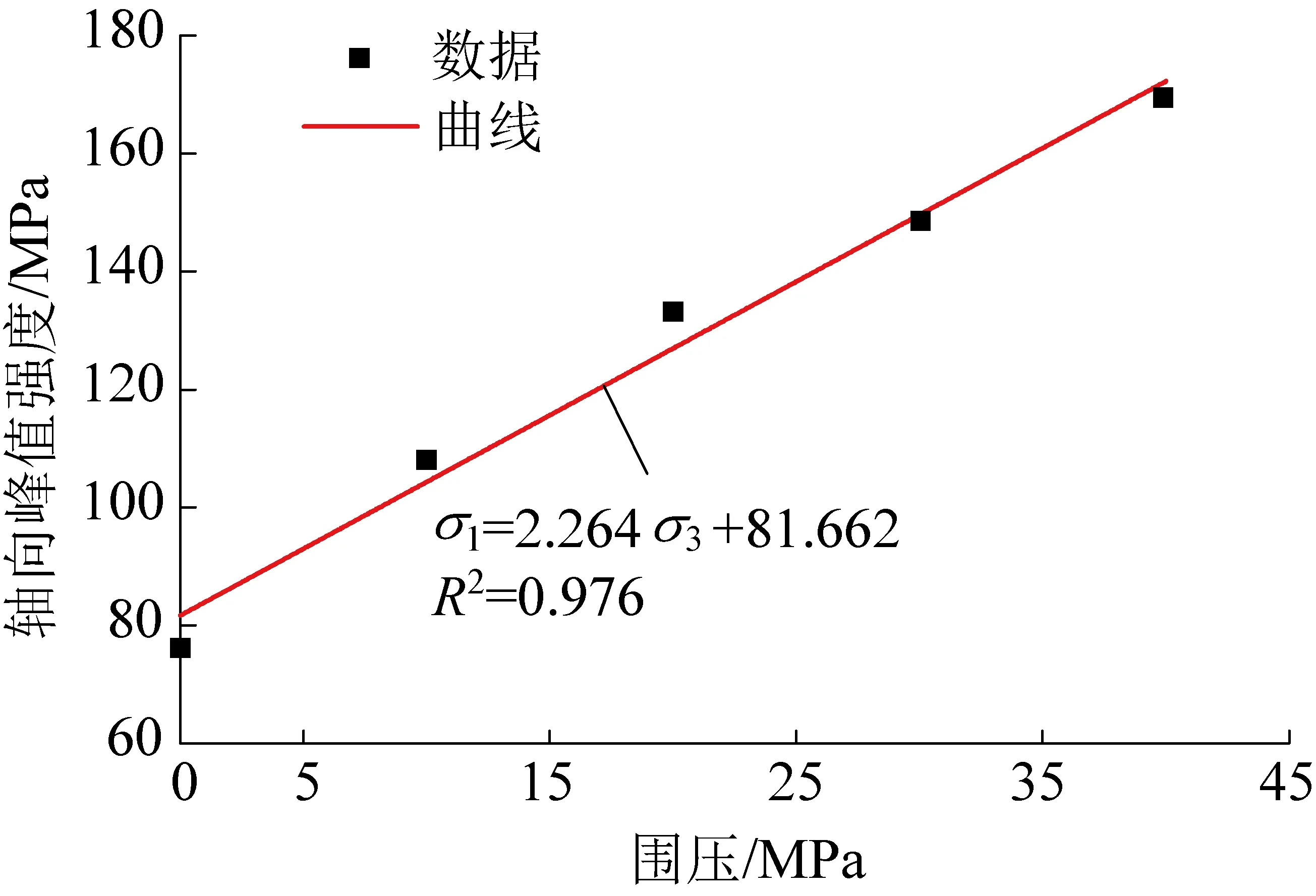
图2 围压与峰值强度的关系

由图2可知，岩石的最大主应力(轴向峰值强度)与最小主应力(围压)之间满足线性关系。由莫尔应力圆理论，确定出岩石的黏聚力为27.292 MPa，内摩擦角为22.784°。

1.3 岩石破坏能量演化特性分析

由文献[11-12]可知，一个单位体积的岩体单元在外荷载作用下，外力对于岩石做功输入能量W为

W=We+Wd

(1)

式中：We为弹性能，MJ/m3；Wd为耗散能，MJ/m3。

外力对于岩石做功输入能量W[13]为

(2)

式中：σ1为轴向应力，MPa；σ3为径向应力，MPa；ε1为轴向应变；ε3为环向应变。

在三轴压缩试验中，弹性能公式

(3)

式中：E0为初始弹性模量，GPa；μ为泊松比。

1.4 砂岩加载破坏能量演化分析

总能量确定方法：通过软件Origin对轴向应力-应变和环向数据应力-应变分别进行面积积分得到积分后新数据，将积分后的数据进行相加就得到岩石加载过程中的总能量；单元弹性能确定方法：先确定出在不同围压作用下岩石的弹性模量和泊松比，将不同围压条件下的轴向应力-应变、环向应力-应变数据、弹性模量和泊松比数值代入到式(3)中就可以确定出岩石在加载过程中的弹性能数据。根据上述能量计算方法得出单轴和三轴压缩能量试验曲线如图3所示。

图3 能量演化曲线

由图3可知，在单轴压缩试验中，在弹性阶段(即在屈服点之前时)，岩石的弹性能曲线与总能量曲线基本重合，此时耗散能曲线基本与x坐标轴重和；在屈服点之后峰值应力点之前，弹性能曲线虽然继续增大，但是耗散能曲线也开始呈现出增大趋势(即弹性能增长率有所减缓)，此时岩石单元体积内部微裂隙扩展速率逐渐加快；在曲线峰值点之后，原来储存的弹性能瞬间释放，导致岩石内部裂隙贯通形成宏观裂缝，最终导致岩石失稳破坏。弹性能变化规律与岩石应力-应变曲线变化规律基本一致；总能量的变化规律在加载初始时刻与弹性能的变化规律基本重合，虽然在接近峰值应力点时突然增大，但能量增长速率却渐趋缓慢；最后，在峰值点时弹性能全部释放导致岩石破坏，进入峰后残余阶段。

根据峰值点能量数值，绘制岩石峰值能量随围压的规律曲线如图4所示。由图4可知，随着围压的增大，岩石弹性能和总能量在峰值点处的能量基本呈现线性增大趋势，且常规三轴压缩时的能量远大于单轴压缩时的能量，说明随着围压的升高，外部输入的能量转化为弹性能的能力逐渐增大，围压可以有效提升岩石的储能能力。

2 岩石损伤统计本构模型的建立

由文献[14]可知，应力、弹性能和弹性模量之间存在以下关系

(4)

式中：σ1c为单轴压缩试验的峰值强度，MPa；E为弹性模量，GPa。

根据广义胡克定律和应变等效原理可知，

(5)

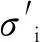
岩石在常规三轴压缩作用下满足以下条件

(6)

则将式(6)代入到(4)中得到单元弹性能We与轴向应变ε1的关系为

(7)

式(7)就是基于能量耗散率构建的非线性演化模型，来预测在加载过程中弹性能随着应变的演化规律。式(7)中具有环向应变ε3，使得弹性能和轴向应变之间不能建立良好的对应关系，故首先需要建立轴向应变与环向应变的关系，进而建立能量演化非线性模型。

岩石的轴向应力-应变关系和环向应力-应变关系做比值可以得出

(8)

为了计算简便，在此对式(8)进行简化，引入表示应力状态的参数λ，令其满足以下关系，有

(9)

则轴向-环向应变关系式为

ε3=λε1

(10)

可以得到弹性能与轴向应变的关系为

(11)

对于损伤变量D而言，不仅需要可以描述岩石内部特性变化关系的内变量，且损伤变量模型表达式尽量简单，笔者将采用统计损伤力学来建立岩石在加载过程中的损伤变量模型。

根据KACHANOV[15]对损伤的定义以及岩石微元在发生破坏时屈服函数F满足Weibull分布函数[16]，得到损伤演化方程为

(12)

式中：m、F0为分布参数，进而得到能量非线性演化本构方程为

(13)

结合有效应力原理可知，Mohr-Coulomb破坏准则的表达式[17]如下

(14)

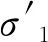
其中试验参数α、β满足以下条件

(15)

式中：c为黏聚力，MPa；φ为内摩擦角，(°)。

3 岩石能量非线性演化本构模型参数

3.1 模型参数推导

对于分布参数m、F0一般通过不同条件下应力-应变曲线特殊点关系确定(图5)。

We—弹性能；Wec—弹性能峰值；ε1c—应变峰值；ε1—不同应力方向上的应变

由能量演化曲线[18-20]可知，岩石在加载变形至峰值点时，其弹性能演化曲线存在以下几何关系：①ε1=ε1c时，有We=Wec；②ε1=ε1c时，有∂We/∂ε1=0。同时，岩石的应力-应变曲线也满足以下关系：③当ε1=ε1c时，有∂σ1/∂ε=0；④当ε1=ε1c时，有σ1=σ1c。

由条件①得出

(16)

由条件②得出

(17)

将We作为ε1的函数，结合式(13)对式(17)在峰值点处展开得

(18)

式中：ε1c为峰值应变，%；F1c为岩石在峰值点处的微元强度值，MPa；D1c为峰值点处损伤变量值;λc为参数λ在峰值点处的数值。

在峰值点处屈服函数F的一阶导数为

(19)

将式(19)代入到式(18)中，可以得到We关于ε1的完整表达式。

岩石在常规三轴压缩作用下(σ1>σ2=σ3)，在峰值点处的应力-应变关系满足以下条件

(20)

将式(19)和式(20)代入式(18)中得分布参数m为

(21)

式中：B为参数，可表示为

(22)

分布参数F0在峰值点处为

(23)

其中，F1c、D1c和λc具体可以表示为

(24)

(25)

(26)

3.2 岩石力学物理参数确定

根据三轴室内试验数据，可以得出在不同围压条件下砂岩的弹性参数变化规律如图6所示。

图6 围压与泊松比和弹性模量关系

由图6可知，随着围压的增大弹性模量和泊松比均增大，说明围压增大提升了岩石抵抗变形及承受荷载的能力，使得砂岩更不容易产生破坏。

3.3 岩石损伤模型参数确定

结合上述岩石分布参确定方法，将不同围压条件下的峰值应力、峰值应变、峰值处的损伤变量值、强度值以及文中简化的参数值代入，便可以求出分布参数m和F0的具体值见表2。

表2 参数计算值

上述计算确定的分布参数只是在特定围压下的分布参数值，并不能完全代表所有情况下分布参数与围压之间的关系。故根据表2中不同围压作用下的分布参数对参数进行适当的修正，其修正曲线如图7所示，修正公式见式(27)和式(28)。

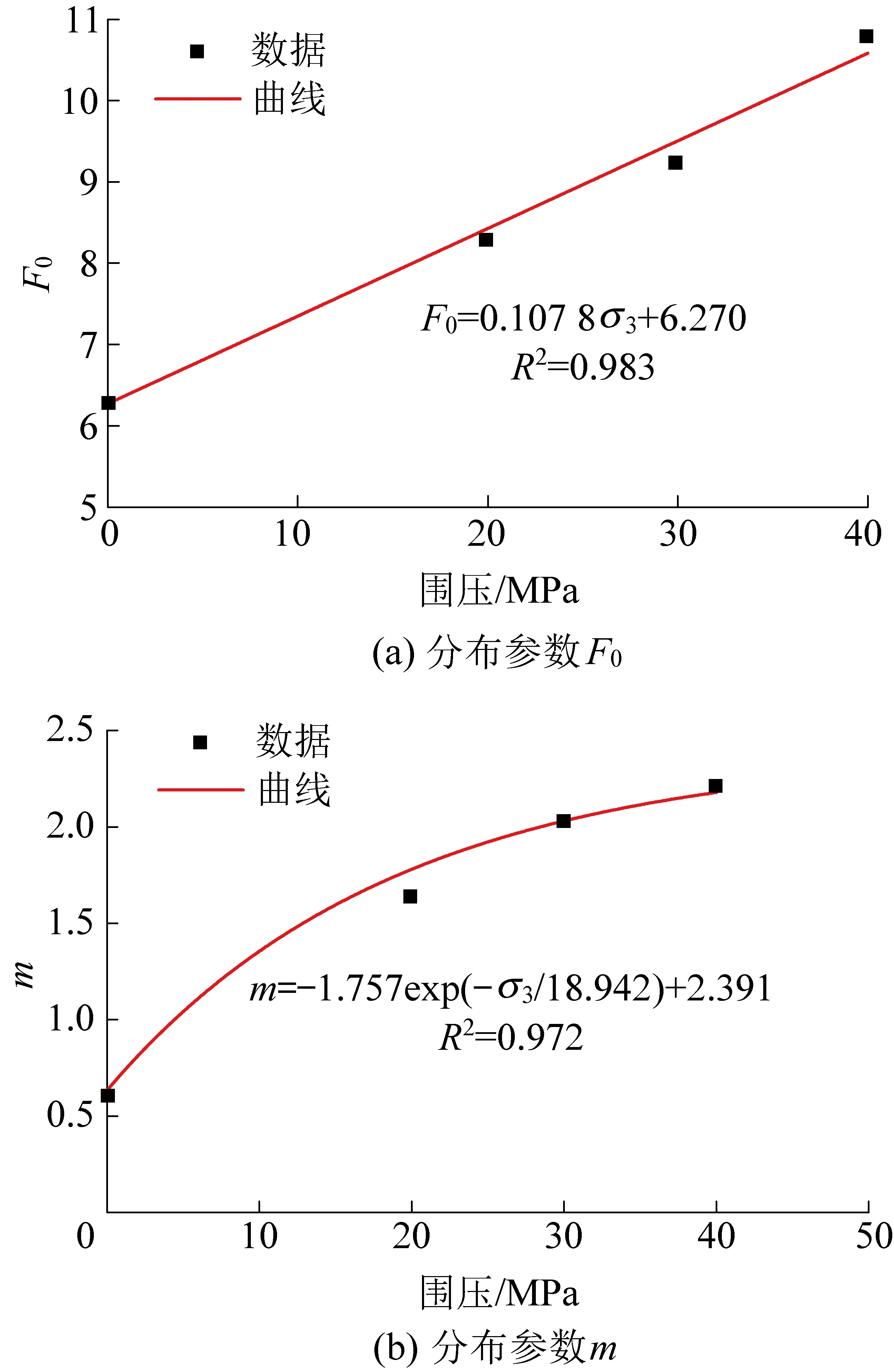
图7 分布参数与围压关系

由图7可知,分布参数与围压之间拟合程度较好，相关性系数在0.95以上。

m=-1.757exp(-σ3/18.942)+2.391

(27)

F0=6.270+0.107 8σ3

(28)

3.4 分布参数的物理意义

为明确建立能量非线性演化模型中的分布函数中m和F0的物理意义，以表2中的试验数据及能量非线性演化模型进行分析,如图8所示(以围压10 MPa为例)。

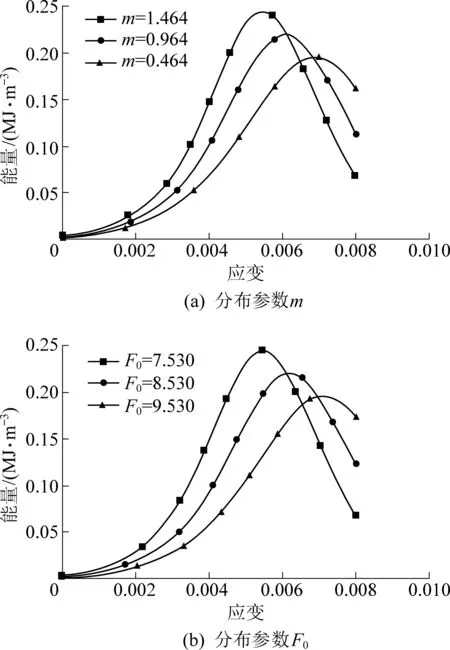
图8 分布参数分析

由图8可知，当分布参数F0固定时，砂岩的弹性能-应变曲线的峰值点能量随着分布参数m的增加而增加，故参数m反映了岩石的极限储能能力，即参数m越大，岩石储能能力越强。当分布参数m固定时，砂岩的弹性能-应变曲线的峰值点能量随分布参数F0增加而减小，且曲线弯曲度也越来越大(逐渐向x轴靠拢)，故参数F0越大，岩石的储能速率就越小，也就是岩石在变形过程中释放的能量越多，使得岩石更加容易发生破坏。

4 模型验证与对比

将式(27)和(28)代入式(13)中便可得到岩石修正参数后的能量非线性演化模型。笔者以围压10 MPa和围压30 MPa为例。为了更好地验证笔者建立的能量演化模型的正确性与优越性，借用了文献[7]中的大理岩破坏过程能量非线性演化模型。通过笔者的试验数据对文献[7]中能量非线性演化模型的参数进行确定，并绘制出不同围压条件下砂岩能量非线性演化模型曲线，再与本文的模型曲线以及试验数据进行了对比分析如图9所示。

由图9可知，比较分析得到：在峰前阶段，模型曲线与试验数据拟合程度较高；在峰后阶段，模型曲线也可以较好地描述弹性能与轴向应变之间的关系，模型曲线与试验曲线具有良好的拟合度。这表明该模型更加接近围岩实际的变形破坏演化规律，建立的模型可以较好地反映岩石弹性能-应变变化关系，且笔者所建立的模型中的参数都可以通过试验进行确定，引入的分布参数也具有明确的物理意义。模型曲线和文献[7]中的模型曲线都可以较好地描述弹性能与轴向应变之间的关系，但是文献[7]只能描述峰前阶段曲线变化规律，而笔者建立的模型也可以对岩石峰后能量-应变曲线的变化规律进行描述。

5 结 论

1)模型曲线和能量积聚演化模型曲线都可以较好地描述弹性能与轴向应变之间的关系，但是文献[7]只能描述峰前阶段曲线变化规律，而笔者建立的模型也可以对岩石峰后能量-应变曲线的变化规律进行描述。

2)能量非线性演化模型曲线与试验数据拟合程度较高，可以较好地反映岩石弹性能-应变的变化关系。该模型中的大多数参数都可以通过试验进行确定，引入的分布参数也具有明显的物理意义，且分布参数与围压之间拟合程度较好，相关性系数在0.95以上。

3)虽然模型曲线与峰后试验曲线有较大的偏离，但本文模型不仅能描述峰前阶段曲线变化规律，也对峰后曲线变化规律有所描述，弥补了原有能量模型不能描述峰后曲线变化规律的缺点。

4)岩石的最大主应力(轴向峰值强度)与最小主应力(围压)之间满足线性关系。由莫尔应力圆理论，确定出岩石的黏聚力为27.292 MPa，内摩擦角为22.784°。