铈基抛光粉抛光工艺的多响应稳健优化设计

李春丽， 李欢欢， 卢虎生

（内蒙古科技大学经济与管理学院，内蒙古 包头014000）

0 引 言

化学机械抛光（Chemical Mechanical Polishing，简称 CMP） 是在 1965 年由 Walsh 和 Herzog 首次提出的[1]，该技术是近十几年发展的新一代超精密表面制造方法，是目前最为主流实现全局平面化的工艺技术[2]，该技术已逐渐被应用于各种需要表面平整处理的工件。 Steigerwald 等对CMP 技术所采用的设备及用品进行了列举[3]。 其中在材料的选择方面，由于抛光浆液的性能直接影响抛光后表面的质量， 所以选择性能好的抛光浆料，是高抛光速率和好平整度的保证。

目前，铈基稀土抛光粉因其光洁度高、使用寿命长、 操作环境清洁等优点成为了抛光公认的首选粉体，在衡量其在抛光工艺过程中的质量指标中，抛光粉的切削率、粉的悬浮性以及抛光粉浆料的流变性等指标成为了关键的质量要素。但是由于在实际的生产中稀土抛光粉使用不规范，与所生产产品要求的质量不匹配，缺乏完整系统的质量管理体系，在加工过程中不注重使用可靠的质量改进和控制技术而多选择事后控制，这些都造成了稀土资源的浪费。 尽管国内有学者探索了从抛光废料中回收稀土，但是工艺产生的废渣太多并不能从本质上解决问题[4]。

著名质量管理专家田口认为，产品质量首先是设计出来的，其次才是制造出来的，因此质量控制需要从制造阶段进一步提前到设计阶段。 稳健设计的理念从对实物问题解决型到为满足客户多重需求的技术开发型进行了转变[5]。稳健设计是针对各种误差因素具有强有力的抗干扰设计方法， 该方法具有能有效地减小产品性能的波动、大幅提高系统稳健性的优点，逐渐被人们所重视。 国内外许多统计学家和质量管理学者在质量控制方面进行了深入研究，对稳健设计方法不断的进行改进以解决多响应稳健优化的问题。其中满意度函数法是一种简单易行的稳健优化方法，Derringer 等利用加权几何平均思想构造综合满意度函数[6]。Shah 等指出如果响应变量的交互关系较大时满意度函数法得到的结果并不准确[7]。 为此，国内外学者也对满意度函数同其他方法结合对其进行改进，Lee 等利用PCI 和逻辑需求函数来解决多特性参数设计问题[8]。Wu 在研究中提出一种改进的双指数满意度函数法[9]。伍建军等通过引入熵权理论改进的综合满意度函数，将双响应优化问题转化为求综合满意度函数最大值的简化问题[10]。 此外，学者也采用了其他方法解决多响应之间的相关性问题，Joseph 等提出多元损失函数以考虑了响应之间的交互作用[11]。 Vining 与Ko 等多位学者对损失函数进行扩展，排除因子之间的干扰以及考虑过程的经济型[12-13]。 同时，马义中[14]、崔庆安[15]、张旭涛[16]、周志伟[17]等多位学者都通过采用一定的辅助或改进手段， 以达到降低多响应之间的交互性甚至在参数设计阶段消除质量特性之间的相关性的目的。但是在解决多响应交互作用问题时，所采用的优化方法往往忽略了响应的权重从而方法带有一定的主观性。 为解决多响应权重确定的问题，钟慧敏等利用Ke ndall 协同系数检验和熵权理论来确定多元稳健设计中质量损失函数的权重[18]。 伍建军等通过主客观权重法科学设置了各响应均值和方差质量损失的权重[19]。

然而，在实际产品开发与设计时，除了要考虑样本数据自身的客观信息，工程师或者实验者的主观先导经验也对所做决策有着不容忽视的作用。 同时，信噪比作为衡量结果稳健性的指标，可用其代替方差作为判断数据与其目标值的偏离程度。 为此，采用信噪比代替方差作为响应变量，在考虑各响应的主客观权重基础上，将其融入到满意度函数中以构建综合满意度函数模型， 达到铈基抛光粉CMP 工艺过程的稳健性优化并获取高性能抛光液的目的。

1 基于信噪比的多响应稳健优化设计方法

1.1 综合权重的确定

确定主观权重的方法有层次分析法、 专家打分法、平均赋值法等多种方法，同样的，确定客观权重的方法也有很多。通过同从事稀土抛光材料研发与应用方面的工程师进行访谈，明确各目标响应的重要程度占比相当，另外，考虑到熵权法主要依据客观样本数据，几乎不受主观因素的影响，故本文采用熵权法确定客观权重，平均赋值法确定主观权重。 在确定客观权重时，需要将指标属性统一，否则无法对最终的评价结果进行判断。 指标根据自身属性，可以分为正向指标、逆向指标和适度指标。 如果选取的指标既有正向指标，又有逆向指标，还有适度指标，可按照极值法将其标准化。

针对正向指标，计算公式为：

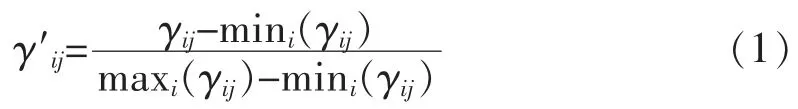
式（1）中：γ′ij表示标准化之后的指标值；γij表示指标值，maxi（γij）表示指标中的最大值；mini（γij）表示指标值中的最小值。

针对逆向指标，计算公式为：

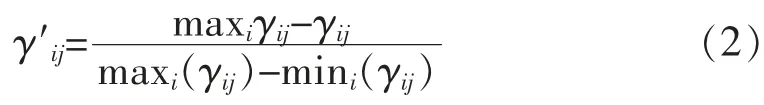
式（2）中：γ′ij表示标准化之后的指标值；γij表示指标值；maxiγij表示指标中的最大值；mini（γij）指标中的最小值。

针对适度指标，计算公式为：

式（3）中：φ′ij表示标准化之后的指标值；φij表示指标值；maxiφij表示指标中的最大值；miniφij表示指标中的最小值。

第j 个指标的熵值的计算公式为：

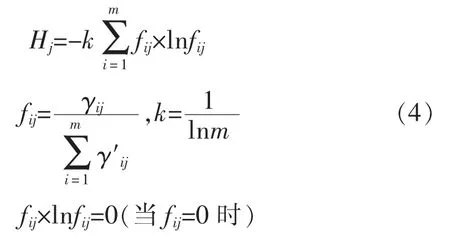
式（4）中：Hj表示第 j 个指标的熵权值；fij表示指标值；fij表示第j 个指标下第i 个样本占该指标的比重。

第j 个指标熵的权重定义为：

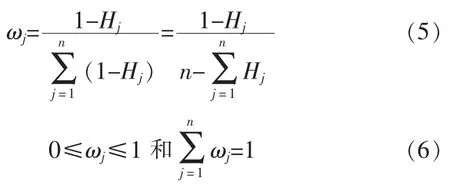
其中：ωj表示第j 个指标的权重值；1-Hj是第j 项指标的差异数，既对第j 项指标熵值越小，指标变异程度越大。

将所得到的客观权重ωj对主观权重εj进行修正，可得到综合权重Wj[20]。 第j 个指标熵的综合权重可定义为：

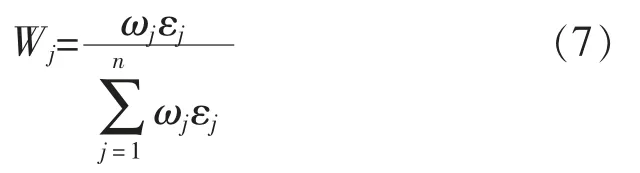
1.2 信噪比

田口教授根据不同的质量特性提出特定的信噪比公式。 其中：η 表示为信噪比；yi表示输出响应值；表示均值估计值；q 为试验次数；s2是方差估计[12]。

望小质量特性的信噪比：

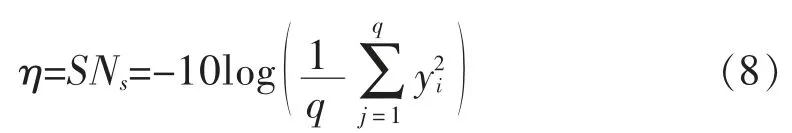
望目质量特性的信噪比：

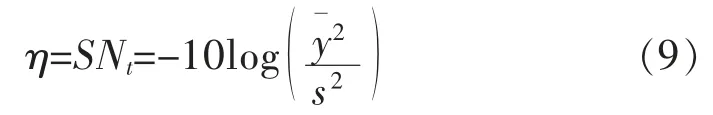
望大质量特性的信噪比：

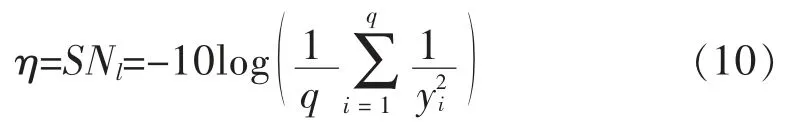
1.3 满意度函数的建立

对于不同类型的质量特性其满意度函数的构建方式是不同的，质量特性可分为望目、望小和望大3 种特性。构建模型时一般假设第i 个响应的满意度值为 d（yi），目标值为 Ti，上下规格限分别用 USLi，LSLi表示。

望目情况下的满意度函数定义为：

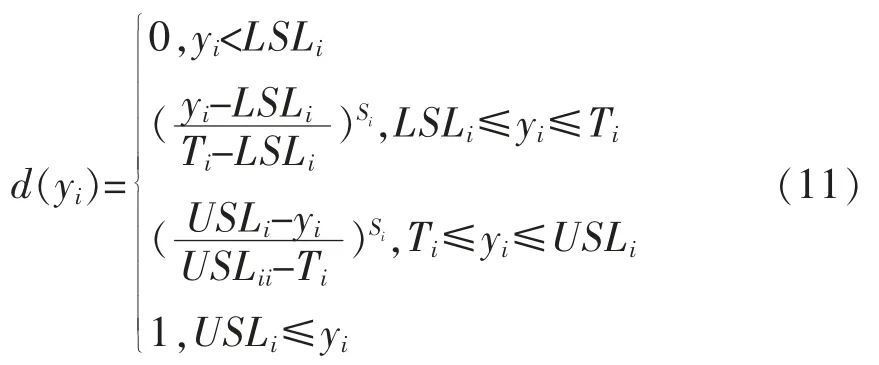
望小情况下的满意度函数表达式定义为：

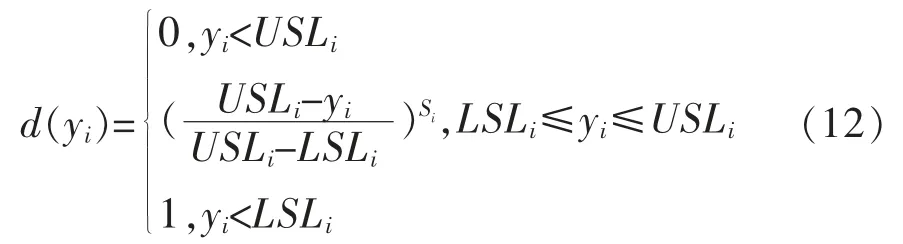
望大情况下的满意度函数定义为：

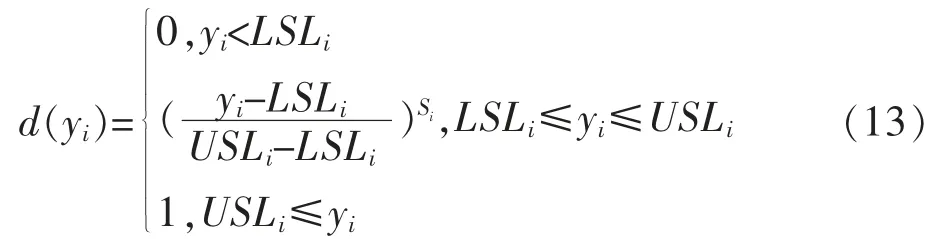
通过计算每一个响应的满意度函数，可以构造综合满意度函数，但该满意度函数是基于每个满意度的权重都相同的情形，其形式如下：

其中：D综合表示综合满意度，d（yi）表示第 i 各响应的满意度函数，i=1，2，3，…，n。

Derringer 提出改进加权平均的方法构建综合满意度函数[21]，其综合满意度定义为：

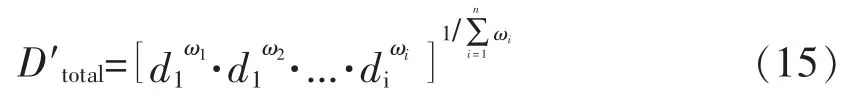
式（15）中：D′total表示为改进的满意度函数值；di与 ωi分别表示第i 个响应的满意度函数和权重，0≤ωi≤1且满足

1.4 基于信噪比与满意度函数的稳健优化设计模型

信噪比作为评估产品或生产过程质量的标准，对其优化可以保证产品的质量和结果的稳健。基于信噪比与满意度函数的稳健优化设计模型的构建； 首先，是在正交试验结果的基础上，确定各质量特性的信噪比；然后，将计算所得到的信噪比作为新的质量特性变量确定其主客观权重；其次，将信噪比同满意度函数方法结合起来， 建立新的多响应稳健优化设计模型；最后，构建加权几何平均综合满意度函数。信噪比作为衡量结果稳健性的指标，其值越大越好，故转化为望大特性的满意度函数，其表达式定义为：

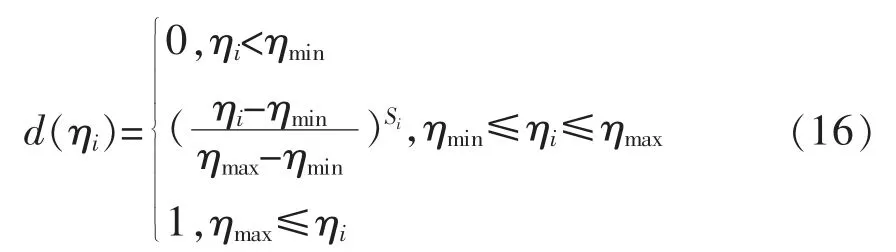
其中，d（ηi）表示为第i 个信噪比的满意度值且取值在（0，1）的范围内，ηmax和 ηmin表示为信噪比的上下规格限。

依据计算所确定各响应的信噪比和主客观权重，利用加权平均的方法所构建的综合满意度函数模型如下：

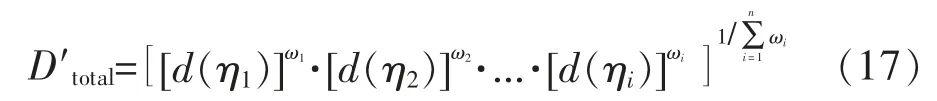
其中，d（ηi）与 wi分别表示第 i 个信噪比的满意度函数和权重。

2 铈基抛光粉CMP 工艺的多响应稳健优化设计

实验样品和实验设备均由包头某稀土抛光粉有限公司提供，实验的主要过程是以铈基抛光粉作为抛光浆料对K9 光学玻璃进行化学机械抛光实验，分析抛光时间、抛光盘转速、固含量、pH 值对抛光粉切削率（微米/分）和玻璃划痕度（分）的影响，确定满足稳健性的较优工艺参数水平组合从而制备出高性能的抛光液。

2.1 试验数据

实验选用0603 稀土抛光粉作为抛光浆液，K9玻璃作为被抛光工件，在双面抛光机上面进行抛光作业，研究抛光时间、抛光盘转速、抛光浆液固含量、pH值这4 个可控因子对抛光粉切削率和玻璃划痕度的影响， 根据因子特征安排了4 因素3 水平的正交实验，实验因素与水平如表1 所列。 在上述因素中，“时间”和“转速”是指抛光机处于重压阶段的抛光时间和抛光盘转速；“固含量”和“pH 值”是指抛光液进入设备之前的固含量值和pH 值。

表1 可控因子及其水平Table 1 Controllable factors and their levels

用L9（34）正交表进行实验设计，其试验数据采集的方法为：在每种工况（每个实验号）条件下进行抛光5 车测定， 测定抛光粉每车下来的切削率和划痕度，然后将5 车测定的各项数据记录并求其平均值得到实验结果。切削率和表面光洁度分别用Y1和Y2，且两者均为望大的质量特性，将其标准化之后根据式（10）计算出各响应的信噪比并分别用η1和η2表示，试验方案与试验结果如表2 所列。

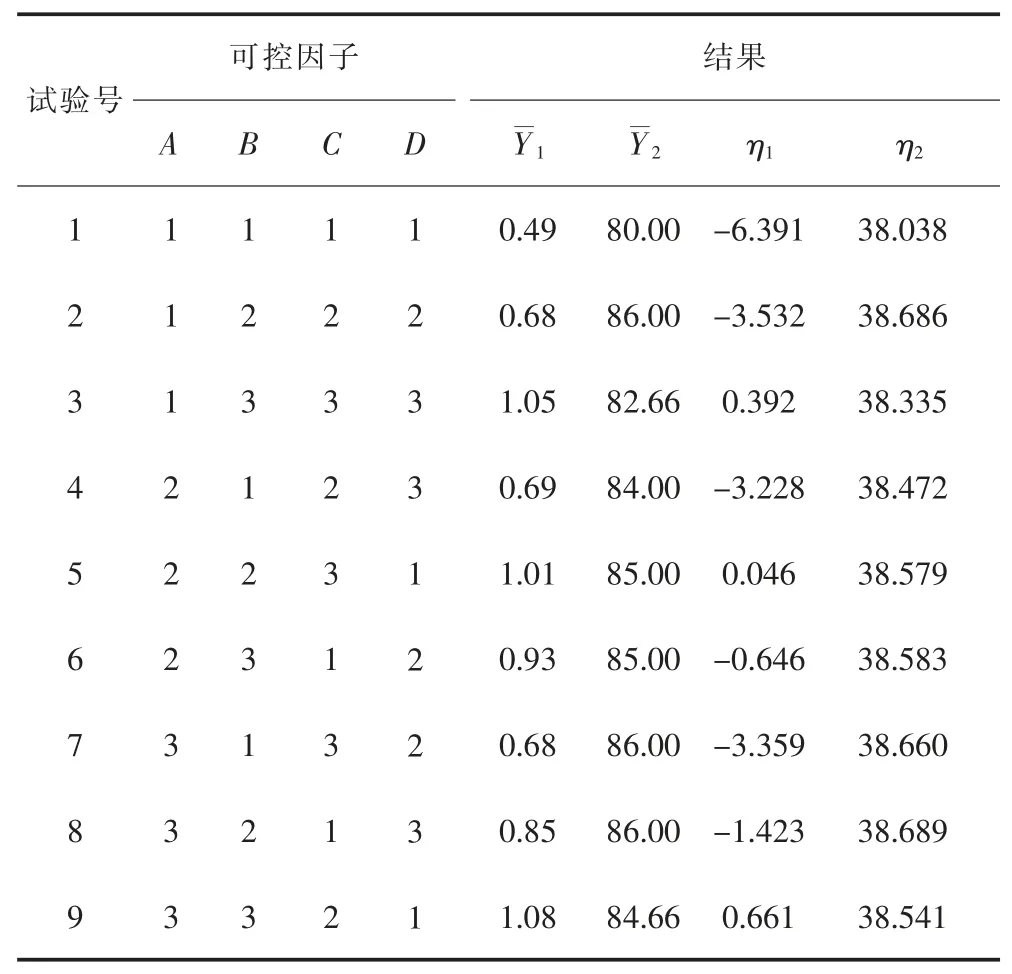
表2 正交试验结果及信噪比值Table 2 Orthogonal test results and SNR

2.2 结果分析

在对正交试验设计优化中，极差分析法是寻找最优工艺常用的方法之一。采用极差法分析计算的切削率和表面光洁度的结果见表3。

通过对表3 的分析，可得出对切削率影响从大到小的因素依次为： 抛光粉固含量>抛光时间>抛光盘转速>pH 值；对划痕度影响从大到小的因素依次为：抛光时间>pH 值>抛光盘转速>抛光粉固含量。 综合以上2 个方面的因素，联系实际研究生产，得出达到切削率和划痕度较优时抛光粉CMP 工艺的较优工艺为：A2B2C2D2， 即较优工艺条件为重压段抛光时间为3 600 s，重压段抛光盘转速为27 r/min，抛光浆固含量为10%，抛光浆pH 值为7。

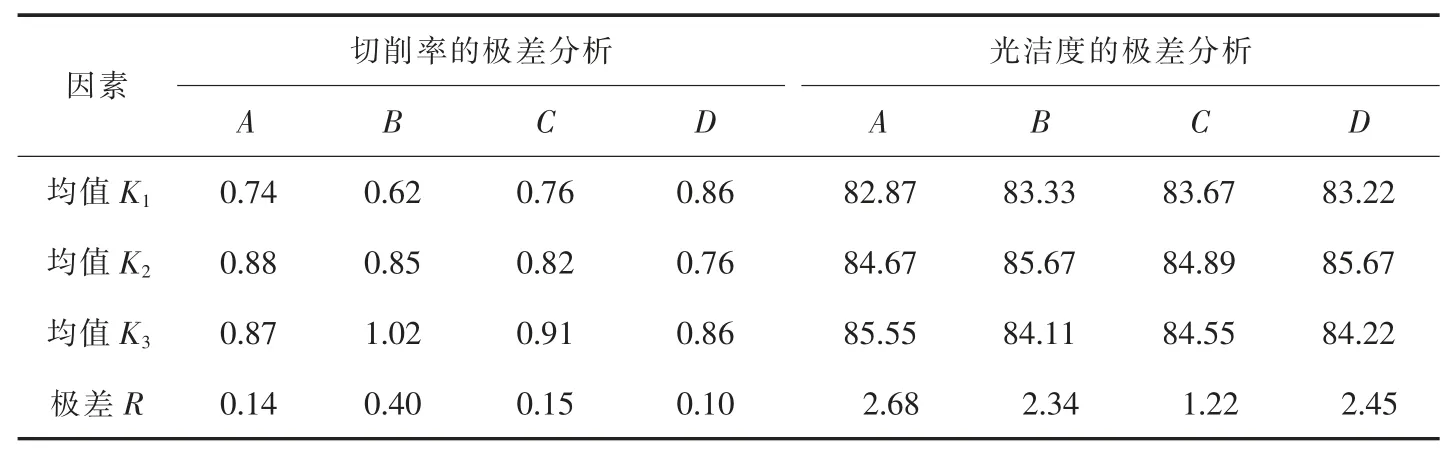
表3 切削率和划痕度的极差分析Table 3 Range analysis of cutting rate and scratch degree

根据表2 所示的各个响应信噪比值计算各响应的主客观权重占比，另外由于各响应信噪比均为正向指标，为了消除不同响的量纲影响需根据式（1）将其标准化，并依据式（4）、式（5）计算客观权重其结果如表4 所列。

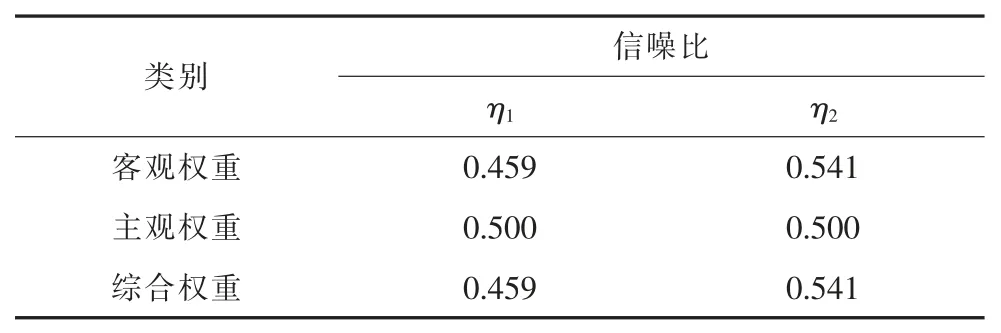
表4 各响应的主客观权重Table 4 Subjective and objective weights of each response

根据表4 得知，客观权重和主观权重两者的计算值相差并不大，此时就无需假设相应的系数以判定主客观权重两者的侧重程度以确定更为合理的综合权重，按照式（7）加权算出综合权重即可。在确定综合权重的基础上，按照不同的质量特性，构建满意度函数，而信噪比作为望大质量特性，故根据式（16）分别构建各响应信噪比的满意度函数，再按照式（17）构建其综合满意度函数式D综合，模型如下：

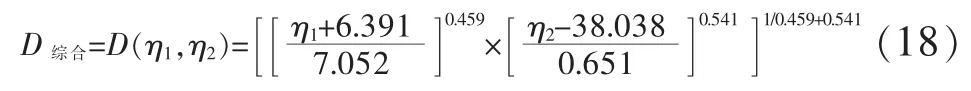
根据基于信噪比所建立的综合满意度函数模型，计算出每一组试验条件下的综合满意度值如表5 所列。

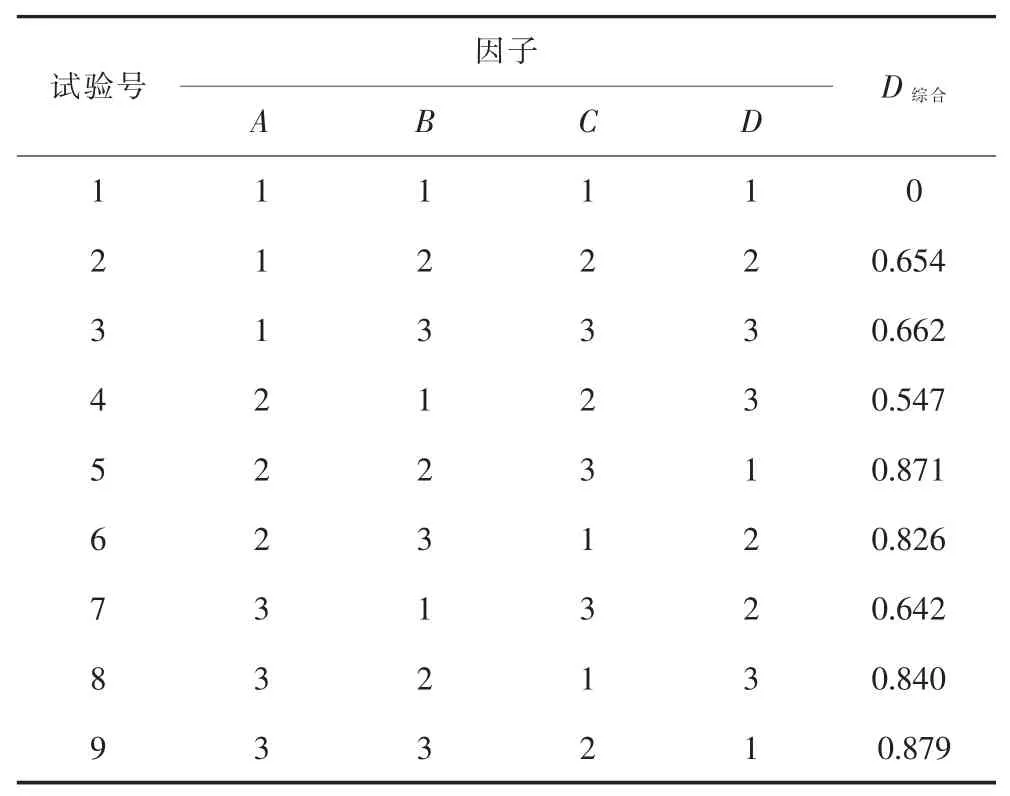
表5 不同试验方案下的综合满意度值Table 5 Comprehensive satisfaction value under different test schemes

通过数值间的比较，由表5 得出稳健设计方案为A3B3C2D1时综合满意度值的达到最大，即较优工艺条件为重压段抛光时间为4 500 s， 重压段抛光盘转速为34 r/min，抛光浆固含量为10%，抛光浆pH 值为5， 此时综合满意度函数值为所有试验方案当中的最大值0.879，一方面表示稀土抛光粉CMP 工艺流程输出的响应偏离目标值的波动程度最小进而表明工艺过程整体上实现了稳健优化，另一方面表示在该工艺条件下稀土抛光浆液满足K9 光学玻璃的抛光质量要求的同时其性能达到较优。

为了验证本文方法的有效性， 将其于传统的满意度函数所优化的结果进行对比。 根据正交试验的各试验方案下的响应信噪比， 在未考虑主客观权重的情况下基于传统的满意度函数D综合， 根据式（14）计算得到每一组试验条件下的综合满意度值， 结果如表6 所列。

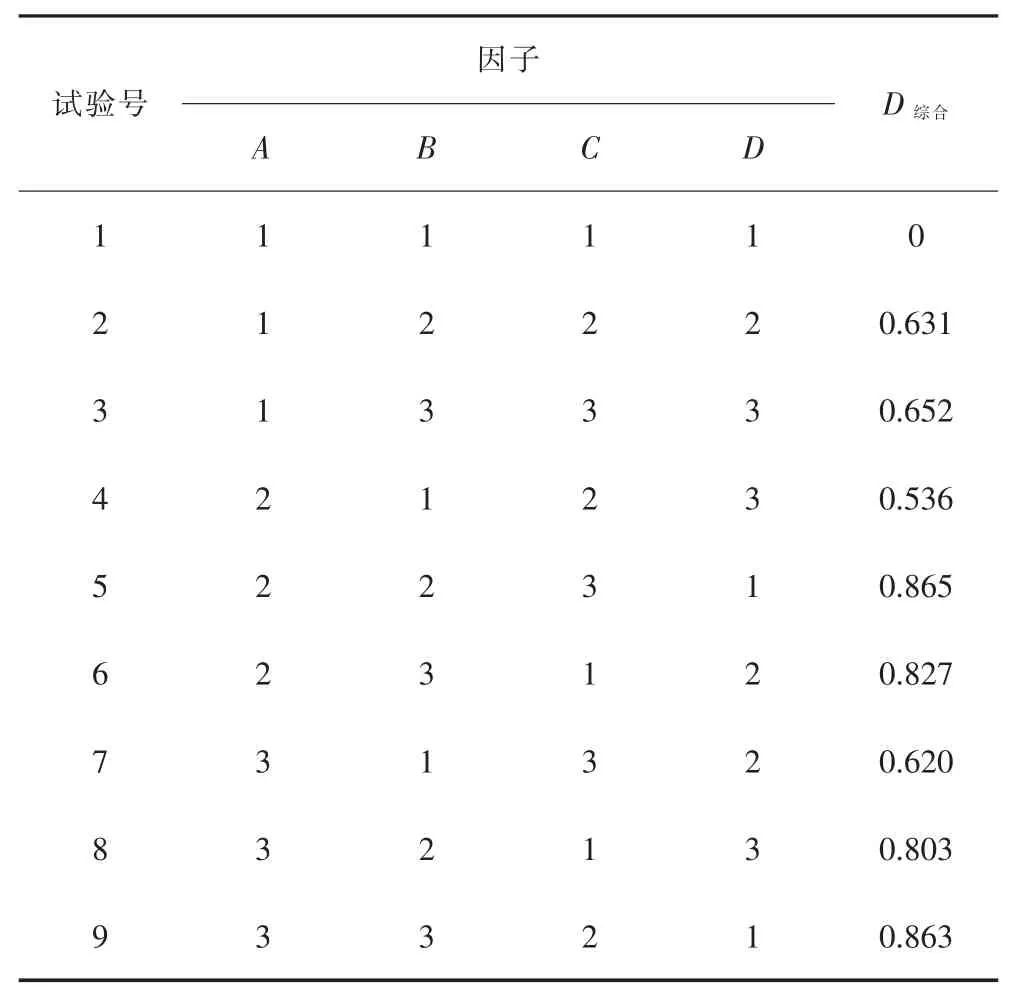
表6 不同试验方案下几何平均综合满意度函数Table 6 Geometric mean comprehensive satisfaction function under different test schemes

综合满意度越大，表明试验方案下的质量特性越好，由表6 可知满意度函数最大为0.865，其稳健设计方案为A2B2C3D1，即较优工艺条件为重压段抛光时间为3 600 s，重压段抛光盘转速为27 r/min，抛光浆固含量为15%，抛光浆pH 值为5。

另外，将本文方法同传统未考虑主客观权重的几何平均满意度函数法以及极差分析法优化的结果进行对比分析，结果如表7 所列。

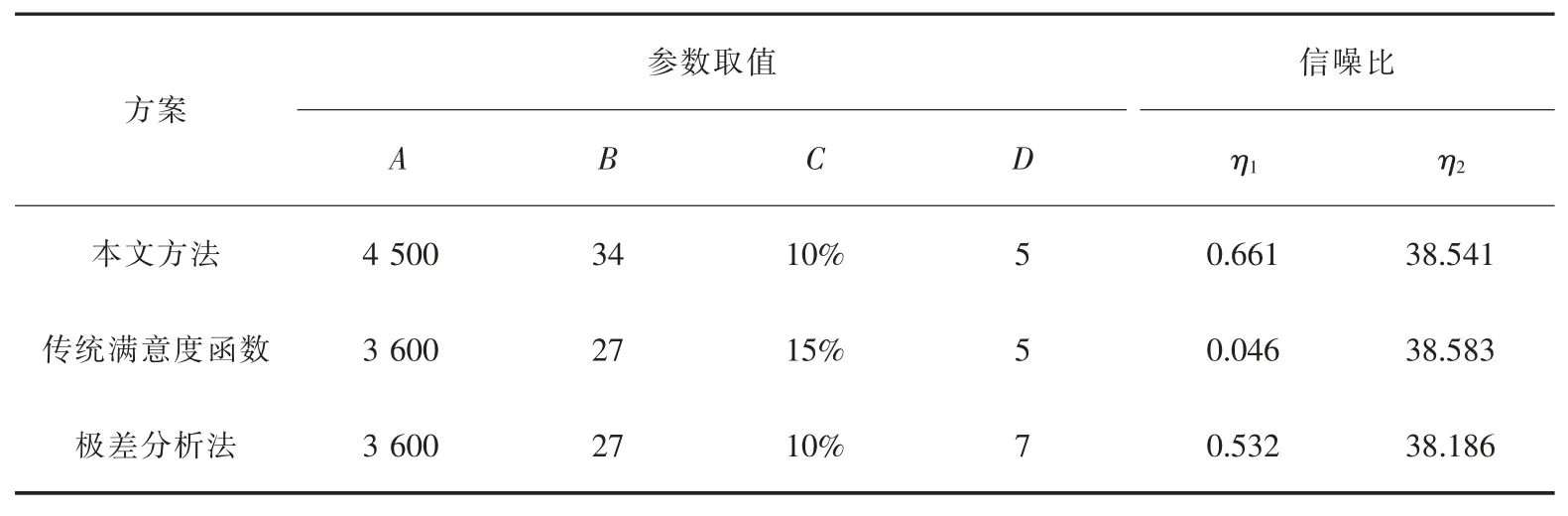
表7 优化结果对比表Table 7 Comparison table of optimization results

从表7 可知， 通过对可控因子进行选择使响应变量达到较优时， 本文方法得到的参数水平组合相较于传统不考虑主客观权重的满意度函数切削率的信噪比提高了0.615，相较于极值法表面光洁度的信噪比提高了0.355。 由于信噪比作为衡量稳健性的指标，其值越大表示受外界干扰的影响越小，质量特性越稳定， 本文所提到的考虑主客观权重基于信噪比与满意度函数相结合的方法优化结果较其他方法使抛光工艺过程更具有稳健性， 此时稀土抛光浆液的性能也达到最大。 结果表明该方法可以有效的达到制备高性能的稀土抛光粉的目的， 同时也有效地解决了CMP 抛光工艺过程的多响应稳健优化的问题，为稀土抛光粉生产企业以及下游应用企业的产品或工艺质量改进方面提供一定的借鉴工具。

3 结 论

为获取使稀土抛光粉抛光工艺的输出响应达到稳健的较优工艺参数组合， 从而实现制备出高性能的稀土抛光浆液的目标，建立了以CMP 工艺流程为研究对象的稳健优化设计模型， 即在考虑主客观权重的基础上， 将信噪比与满意度函数相结合对传统的加权几何平均满意度函数法进行改进， 优化结果表明该方法具有一定的参考价值， 可以为解决类似的多响应稳健优化问题提供新思路。

1）通过对优化结果的比较分析得到较优参数组合为A3B3C2D1， 即较优工艺条件为重压段抛光时间为4 500 s，重压段抛光盘转速为34 r/min，抛光浆固含量为10%，抛光浆pH 值为5，此时的实验条件下抛光粉浆液的性能达到较优；

2）利用信噪比代替响应的方差作为新的响应不仅可以减少由于可分析变量少、数据少而带来的优化损失，而且还可以降低原始响应的波动对质量稳健性的不利影响以获得适用于生产工艺的较优水平参数组合；

3）通过考虑各响应的主客观权重，融合了主客观信息使各响应占比更为合理化，提高了满意度函数求解值的可靠性。