基于不同水肥措施下的桉树二元材积方程研究

黄锋，刘文泉，孔杰君，邱权，何茜，李吉跃，苏艳

基于不同水肥措施下的桉树二元材积方程研究

黄锋，刘文泉，孔杰君，邱权，何茜，李吉跃，苏艳

(华南农业大学林学与风景园林学院，广东 广州 510520)

以不同水肥措施下的20株4年生桉树样木为材料，通过伐倒解析样木收集建模资料。在干形差异分析的基础上，将4个处理分为无施肥与施肥两组处理进行模型拟合。采用模型选优法从6个备选模型中分别筛选出无施肥处理和施肥处理的最优模型。分别将两组处理最优模型的检验结果与广东省韶关市编制的山本和藏式二元材积模型=0.000 12的模型检验结果进行比较，选出误差最小的模型作为该试验地的二元材积方程。结果表明：无施肥处理的最优模型为模型6孟宪宇式，材积方程为=−0.014 675+0.001 078−0.000 105−0.000 155+0.000 050×，施肥处理的最优模型为模型6孟宪宇式，材积方程为=0.067 455−0.009 072+0.000 831+0.028 237−0.000 340。模型6孟宪宇式相较于韶关市编制的山本和藏式，误差更小，精度更高，更适合于该试验地桉树人工林材积和蓄积量的估算。

桉树；单株材积；模型拟合；二元材积方程

在森林资源调查中，蓄积量调查是重要方面之一，它是反映森林原材生产能力的重要指标。森林的蓄积量是由所有林分内林木个数和林木单株材积决定的。材积是反映单株林木体积的指标，受自身生长状况和该地区森林生态变化以及森林经营利用的影响而变化。可持续的森林管理需要对不断增长的蓄积量进行估计以指导森林管理人员估计木材价格和确定砍伐面积，木材蓄积量可以从容易测量得到的树木生长指标中估计出来，最常见的方法是根据材积与胸径和树高等变量之间的关系使用材积方程。应用材积方程估算单株材积降低了野外森林蓄积量调查的难度，提高了调查的效率。尽管材积方程减轻了林业工作者野外调查的负担，但地理位置、气候条件、环境因素、人为干扰和树种遗传等影响都会使树木发生异速生长，导致材积方程的适用范围变得有限，应该针对特定条件、树种和环境编制不同的材积方程或者把不同的变异源作为自变量包括在方程中。由于森林树种丰富度和内部变异性较大，通过收集涵盖足够数量的变异源和树种组合的数据建立适用范围较广的“通用模型”使用起来不切实际，应用性也不强；而建立应用范围较窄的相对精确的模型则可靠性更高。林场级别经营单位的工作者们为了计算林场每年的经济效益而建立的专门适用于该单位的材积表，相较于全国级别和省市级别的材积表，这种材积表减小了误差，提高了查表效率和精度。

桉树()因其适应性强、生长迅速、产量高和木材工业特性好等特点，被广泛用于木材加工制造业，是华南地区主要的工业用材树种。有关桉树材积模型的研究已见报道，如岑巨延应用现代建模思想与方法，优化模型结构，建立了广西桉树二元立木材积动态模型。冯强等以山本材积式为基本模型，对可变参数动态模型进行了模型研建，编制了海南桉树立木材积表。罗明永采用多模型选优和逐步回归法研制了福建省尾叶桉人工林二元立木材积表。这些材积模型的研建都是基于自然环境下生长的桉树人工林，而目前基于水肥管理下的桉树材积模型研究仍目前处于空白。因此，本文以广东省增城市华南农业大学实验基地的桉树人工林为研究对象，基于收集到的代表性样木为实验材料，建立二元材积方程，通过与广东省韶关市编制的材积方程进行对比，选出材积预测误差更小的方程作为该试验地的二元材积预估方程，旨在提高该试验地桉树人工林林分蓄积量的估算准确度。

1 试验地和林分概况

试验地位于广东省增城市宁西镇，该镇位于增城市西南部(23°05′～23°37′ N，113°32′～114°00′ E)。属丘陵地带，地势北高南低，南亚热带季风湿润气候，年均气温21.8℃，年均降水量为2 137 mm，多集中在4—9月。试验地沿着山坡阳面(南面)分成较为水平的五个梯度，面积从北到南(山顶到山底)分别为599.2、1 044.23、1 231.05、1 510.4、1 282.5 m。共5 667.38 m，约0.57 hm。于2017年4月新造林，苗木均为尾巨桉(×)DH32-29无性系组培苗，株行距为2 m × 3 m，初始造林密度为1 667株·hm。

本试验采用随机区组设计，共设置4个不同的水肥处理(表1)，分别为(1)无施肥条件下无旱季补水处理(无水无肥处理，用CK表示)；(2)无施肥条件下有旱季补水处理(有水无肥处理，用W表示)；(3)有施肥条件下无旱季补水处理(无水有肥处理，用F表示)；(4)有施肥条件下有旱季补水处理(有水有肥处理，用WF表示)。每个处理设置5个重复小区，4个处理共20个小区。造林后，于每年的旱季(10月—翌年3月)对试验地W和WF处理进行灌溉补水，灌溉采用滴灌方式，灌溉频率为每周2次，每次连续滴灌4 h。肥料采用桉树专用基肥与追肥，施肥量均与生产桉树用材林的用量一致。基肥和两次追肥分别于2017年3月、2017年7月和2018年7月施于F、WF所有树木中。

表1 试验地水肥处理设计

2 研究方法

2.1 林分调查与样木选择

于2020年7月12日对该试验地所有小区的4年生桉树进行每木检尺，调查指标包括树高和胸径。根据每个处理小区每木检尺结果，计算得出每个处理的平均胸径和平均树高，选取各处理内生长健康，树形良好(无明显受损，树干通直不弯曲不倾斜)且胸径和树高最接近平均值的立木作为样木，每个处理共选5株样木，4个处理共20株。

2.2 样木伐倒与材积测定

样木选好后，下一步进行砍伐工作。伐倒前，应使用油漆笔准确标注树干的根颈位置和胸径位置，并使用喷漆沿着树干基部至胸径处标记南北方向，用油锯或斧头在根颈处进行伐倒后，用皮尺测出实际树干高，用胸径尺测量实际胸径。单株材积采用中央断面区分求积法求得，以2 m为区分段。具体步骤如下：以2 m为段长(第一段长度为2.6 m，其余2 m)，用喷漆在胸径处(1.3 m)，3.6 m，5.6 m，7.6 m……，和树梢(不足1个区分段)底部处标记出需要截取样木圆盘的位置和南北方向，接着对解析圆盘进行截取，圆盘厚度一般为3～5 cm，截取时应尽量使油锯与干轴保持垂直，不可偏斜，同时尽量使断面平滑。圆盘向地的一面要恰好在各分段的标定位置上，以该面为工作面，用来量测直径，另一面为非工作面。每个圆盘锯下后，应立即在当天完成工作面直径测量，避免标本圆盘缩水产生误差。直径测量用游标卡尺分别测量每个圆盘南北、东西两个方向的去皮直径，两者求平均值作为该圆盘的直径。材积计算是利用测得的圆盘直径算出各段的体积，各段体积之和即单株材积，每段的体积为圆柱求积公式，即段长×圆盘面积，梢顶为圆锥求积公式，即1/3梢长×梢底面积，材积具体计算公式如下：

式中：为单株材积(m)，为各区分段断面积(m)，为各区分段长度(m)，g为梢头断面积(m)，l为梢头长度(m)。

2.3 胸高形数计算

胸高形数是林木单株材积与胸高断面积乘以树高的比值，它是反映林木干形的常用指标。其计算公式如下：

式中：为立木的单株材积，为胸高形数，为胸高直径，为树高。

2.4 数据处理与分析

使用WPS excel软件对实测的树高、胸径进行分类整理，用韶关市编制的材积方程得出单株材积理论值，用中央断面区分求积法公式计算出各解析木单株材积实测值，并用公式计算出其胸高形数。使用SPSS 22.0软件对各解析木胸高形数进行单因素方差分析和邓肯式多重比较，并对解析木的树高、胸径和材积进行非线性回归分析。

3 结果与分析

3.1 干形差异分析

若建模样本(表2)之间干形差异较大，将样本总体拟合会降低最终方程的预估精度。因此，在对4个处理的桉树胸高形数进行显著性差异分析的基础上(表3)，再决定是否应该分处理进行建模。CK处理与W处理之间胸高形数无显著差异，F处理和WF处理之间胸高形数无显著差异，CK与F和WF处理之间胸高形数无显著差异，W与F和WF处理之间胸高形数无显著差异。施肥处理与不施肥处理之间干形具有显著差异，说明施肥影响了桉树的干形生长。因此，为了提高材积方程的预估精度，需要将有干形差异的桉树分组建模，即分为施肥与无施肥两组处理进行模型拟合。

3.2 模型回归分析

为了保证研究的准确性以及适应性，从我国林业行业标准《二元立木材积表编制技术规程》(LY/T 2012—2013)推荐的12种二元立木材积模型中选择拟合桉树二元材积式常用的6个回归模型(表4)作为备选模型。以胸径和树高的实测值作为模型的自变量，以通过中央断面分区求积法得到的材积作为模型的因变量，利用SPSS 22.0软件的“非线性回归”功能进行模型的回归分析，将参数a、b、c、d、e初始化为0，选择Levenberg-Marquardt估计方法对各样本数据进行回归分析，最终求得a、b、c、d、e的值。

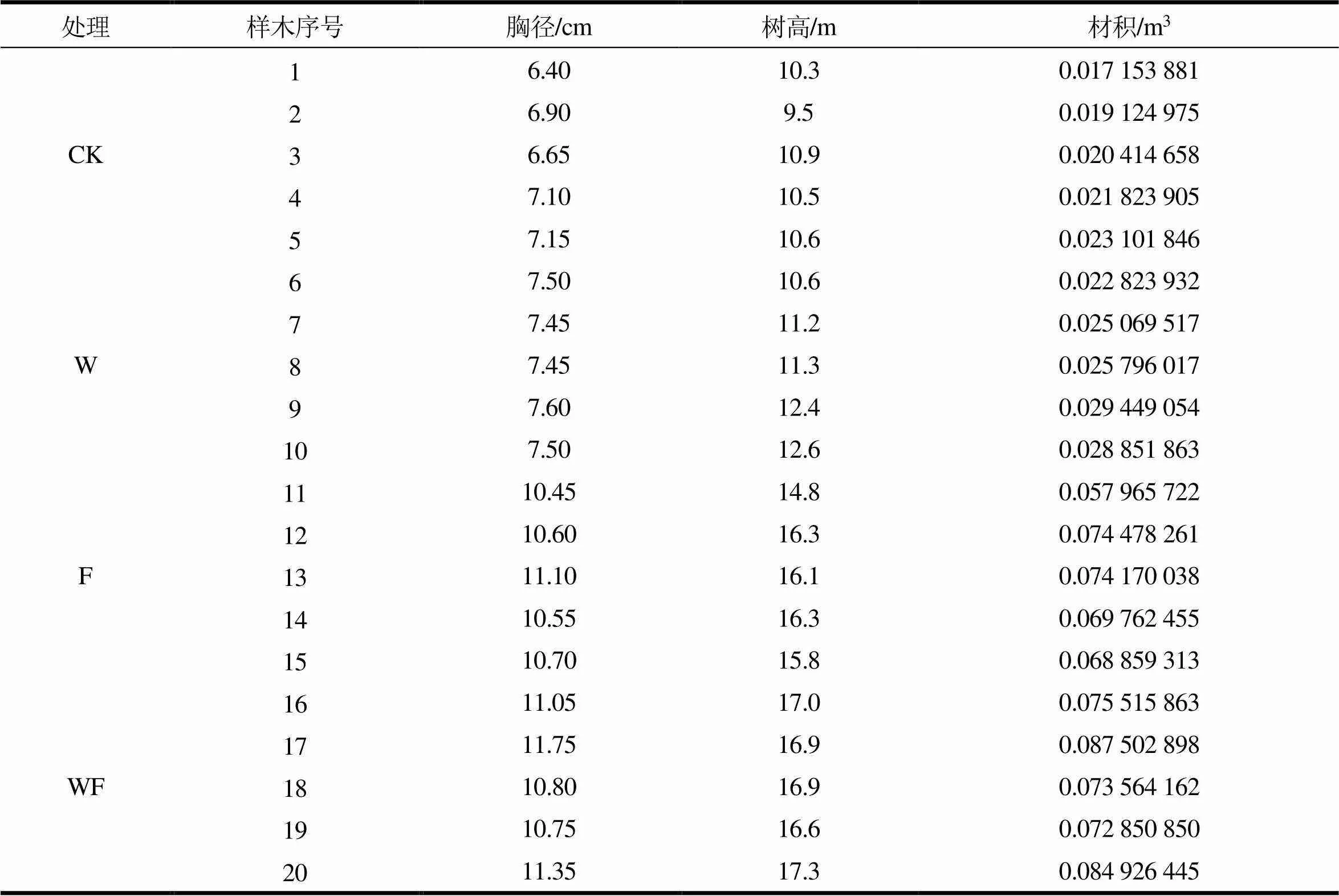
表2 建模样本资料

决定系数越大越接近1，说明胸径和树高与材积之间相关性更高，拟合效果更好。无施肥处理中6个模型的决定系数均在97%以上(表5)，施肥处理的6个模型的决定系数均在90%以上(表6)，说明这6个模型均能较好地拟合无施肥与施肥处理的材积与树高和胸径的关系。在无施肥处理中，模型6的为0.978，稍大于其他5个模型，施肥处理中，模型6的为0.962，明显大于其它5个模型。因此，根据拟合结果得出，无施肥处理和施肥处理的最优模型都是模型6(孟宪宇式)。

表3 处理间胸高形数差异分析

注：表中不同数字后小写字母表示<0.05。

表4 备选模型

表5 无施肥处理拟合结果

表6 施肥处理拟合结果

3.3 模型精度检验

利用模型6(孟宪宇式)和韶关式(山本和藏式)得出的材积理论值与实际值计算出单株材积的误差绝对值，以平均误差绝对值作为模型精度检验的指标(表7～8)。无施肥处理下，模型6(孟宪宇式)的平均误差绝对值为1.87%，韶关市编制的二元材积式(山本和藏式)的平均误差绝对值为3.67%；施肥处理下，模型6(孟宪宇式)的平均误差绝对值为1.67%；韶关市编制的二元材积式(山本和藏式)的平均误差绝对值为12.03%。无论是无施肥处理还是施肥处理，模型6(孟宪宇式)的平均误差绝对值都小于韶关市编制的材积模型。

表7 无施肥处理两个模型精度检验结果

表8 施肥处理两个模型精度检验结果

4 结论与讨论

本研究在干形差异分析的基础上对4个水肥措施下的桉树林分进行分组建模，最终确定模型6(孟宪宇式)为该试验地施肥处理和不施肥处理的二元材积模型。模型6拟合回归得到桉树无施肥处理和施肥处理的两个二元立木材积方程的决定系数均在96%以上，拟合效果良好，方程能很好的拟合树高和胸径的关系。材积方程分别为无施肥处理：=−0.014 675+0.001 078−0.000 105−0.000 155+0.000 050×，施肥处理：=0.067 455−0.009 072+0.000 831+0.028 237−0.000 340。

从两个模型的精度检验结果可知，相较于广东省韶关市编制的山本和藏式材积方程，本研究筛选出的最优模型孟宪宇式提高了对该试验地的桉树材积的预估精度。韶关式编制的材积方程是基于自然条件生长的桉树而编制，未考虑施肥对桉树干形生长的影响，因此在施肥处理中，用韶关市编制的材积式的预测值普遍偏小，误差绝对值均超过了10%。这也应证了土壤养分特征变化会对树木干形产生显著影响，应用相同的材积式估算单株材积可能会导致误差较大。而通过模型6孟宪宇式计算出的两组处理的平均误差绝对值均不超过3%，这表明用孟宪宇式对单株材积的预估准确度可达97%以上，这说明分组建模可以减少组内异速生长给模型带来的影响，是建立更准确模型的可行方法。

模型6(孟宪宇式)具有良好的全面切合性能，可以应用于该试验地桉树人工林单株材积和林分蓄积的估算，但由于本研究样本量较少，未对最优模型(孟宪宇式)进行适用性检验，因此，本研究结果仅对该试验地的单株材积和林分蓄积的估计有效，能否适用于广东省其他地区的桉树林，有待进一步考证。

[1] MAUYA E W, MUGASHA W A, ZAHABU E, et al. Models for estimation of tree volume in the miombo woodlands of Tanzania[J]. Southern forests, 2014, 76(4): 209-219.

[2] 李奇,朱建华,冯源,等.中国森林乔木林碳储量及其固碳潜力预测[J].气候变化研究进展,2018,14(3):287-294.

[3] AKINDELE S O, LEMAY V M. Development of tree volume equations for common timber species in the tropical rain forest area of Nigeria[J]. Forest Ecology and Management. 2006, 226(1/3): 41-48.

[4] 何诚,冯仲科,刘柯珍,等.云杉二元材积与蓄积量精度分析模型研究[J].林业调查规划,2010,35(4):1-6.

[5] 张伟,岑巨延,秦旭东,等.广西杉木胸径和树高二元立木材积模型研究[J].广西林业科学,2020,49(3):397-402.

[6] FELDPAUSCH T R, BANIN L, PHILLIPS O L, et al. Height-diameter allometry of tropical forest trees[J]. Biogeosciences Discussions, 2010,7(5):7727-7793.

[7] 曹忠.立木材积无损精测与建模方法研究[D].北京:北京林业大学,2015.

[8] 国家林业和草原局.中国森林资源报告(2014—2018)[M].北京:中国林业出版社,2019.

[9] 岑巨延.广西桉树人工林二元立木材积动态模型研究[J]. 华南农业大学学报,2007,28(1):91-95.

[10] 冯强,方良.海南桉树立木材积模型研建[J].中南林业调查规划,2014,33(3):47-51.

[11] 罗明永.尾叶桉人工林二元材积表的研制[J].福建林业科技,2009,36(4):170-175.

[12] 王海华.增城区乡土树种人工林生长表现及生态效益评价[D].广州:华南农业大学,2016.

[13] 唐伟东.红松材积与生长性状相关分析及二元回归方程的拟合[J].林业勘查设计,2017(1):42-43.

[14] 吴志华,尚秀华,王睿,等.基于干曲线方程的桉树立木单株材积测算研究[J].桉树科技,2018,35(3):1-8.

[15] 全国森林资源标准化技术委员会.二元立木材积表编制技术规程:LY/T 2102-2013[S].北京:中国标准出版社,2013.

[16] 刘治平,曹宗英,张旭华,等.甘肃省人工云杉林二元立木材积方程的编制研究[J].林业资源管理,2020(1):172-176.

[17] PHIRI D, PHIRI E, KASUBIKA R, et al. The implication of using a fixed form factor in areas under different rainfall and soil conditions forin Zambia[J]. Southern forests,2016,78(1):35-39.

[18] MUGASHA W A, BOLLANDSAS O M, EID T, et al. Relationships between diameter and height of trees in natural tropical forest in Tanzania[J]. Southern Forests: a Journal of Forest Science,2013,75(4):221-237.

Study on Binary Volume Equation ofBased on Different Water and Fertilizer Measures

HUANG Feng, LIU Wenquan, KONG Jiejun, QIU Quan, HE Qian, LI Jiyue, SU Yan

()

Data were obtained from 20 felled 4-year-oldsample trees, that had been grown under different water and fertilizer regimes. Based on stem shape analyses, the four treatments were divided into two groups: no fertilization and fertilization for model fitting. The selection methods used to select the optimal model for no fertilization treatment and the fertilization treatment involved examination of six alternative models. The results of the two groups of optimal models were compared with the model test results of Yamamoto and Tibetan binary volume model=0.000 12compiled by Shaoguan City, Guangdong Province, respectively, and the model with the least error was selected as the binary volume equation of the test site. The results showed that the optimal model of no fertilization treatment was model 6 Meng Xianyu comprising the following:=−0.014 675+0.001 078−0.000 105−0.000 155+0.000 050×. For the fertilization treatment, the optimal model was model 6 Meng Xianyu comprising the following:=0.067 455−0.009 072+0.000 831+0.028 237−0.000 340. Model 6 Meng Xianyu volume model has smaller error and higher precision than Yamamoto and Tibetan volume model compiled by Shaoguan City, whilst also being more suitable for the estimation of individual tree volume and also stand volumes ofplantation in this experimental site.

; individual tree volume; model fitting; binary volume equation

S758.2

A

10.13987/j.cnki.askj.2021.03.003

国家重点研发计划“桉树、马尾松人工林生产力形成的生理”（2016YFD0600201;2016YFD060020102）；国家自然科学基金“桉树人工林生产力对旱季水分输入的变化”(31800527)

黄锋(1997— )，男，在读硕士，主要从事林木生长模型研究，E-mail:249211084@qq.com

李吉跃(1959— )，男，博士，教授，主要从事森林培育研究，E-mail:564857527@qq.com