基于元胞自动机的特长隧道交通流模型研究

孙然然 张静萱 戴泽华 班伟杰 李晓璐 朱广宇*

(北京交通大学综合交通运输大数据应用技术交通运输行业重点实验室1) 北京 100044)(国家铁路局规划与标准研究院2) 北京 100055) (张家口市高等级公路资产管理中心3) 河北 075000)

0 引 言

特长隧道与普通道路相比具有封闭性，行车空间受到限制，易形成交通“瓶颈”，引发交通事故[1].特长隧道内不同区段车辆行驶行为影响因素众多,状态演化复杂多样.针对特长隧道不同区段交通流特性，对车辆驾驶行为进行建模研究，可减少交通事故，提高通行效率.

在早期的交通流模型研究中，主要有宏观模型[2]、中观模型[3]和微观模型[4].其中，微观交通仿真模型因能够描述车辆及车辆之间的相互作用特征被广泛应用，但随着城市化的快速发展，车辆保有量迅速增长，车辆行驶过程中的交互影响变大，能够详细描述与分析复杂微观交通行为的难度进一步加大.近年来，元胞自动机[5-6]模型能较好地揭示各种复杂交通现象的内在机理，且建模与运算规则简单，被一些学者引入到隧道交通流特性的相关研究中.林杉等[7]针对车辆在高速公路隧道路段交通流特性，在双车道元胞自动机模型基础上，引入车速与车道控制条件，提出一种高速公路隧道交通瓶颈元胞自动机模型，分析不同长度隧道对区域路段交通流的影响，该模型能够较好地模拟交通流时空变化特征.吕集尔等[8]改进传统一维元胞自动机交通流模型，随机减速机制采用速度负补偿机制，数值模拟结果显示，通过调节相关参数可改善公路隧道通行能力；刘运霞等[9]首先通过Vissim仿真软件对隧道群进行合理分段,根据车辆平均延误时间及交通事故率确定各路段的最佳限速值，构建元胞自动机模型用于隧道群交通流特性研究.肖承凯[10]在隧道合理分段的基础上，对NS模型中的随机慢化规则进行改进，可较好地模拟高速公路隧道交通拥堵的现象.周林英等[11]通过分析隧道群交通流环境影响因素，改进演化规则，建立事件状态下的元胞自动机隧道群交通流模型，从速度、密度、交通量三方面分析交通流的时空变化规律，仿真结果符合实际情况.Kirytopoulos等[12]考虑隧道灯光、限速以及安全距离等，根据驾驶员的实际反应真实地再现车辆的减速和加速过程，结合车辆能力和动力学的基本机制来描述复杂的交通现象.以上隧道交通流模型研究为分析特长隧道交通流特性奠定了丰厚的理论基础，但大多数模型只是对经典的元胞自动机模型中的某个变换规则进行修改，往往仅通过收集限速区段的交通量、运行数据等确定隧道内最佳限速，考虑参数不全，不能够全面反映特长隧道中交通流特性.

针对特长隧道不同区段车辆行驶的不同特性，首先将隧道分为4个区段.隧道各区段的最佳速度值与道路线性、环境状况和驾驶员视觉特性相关，包含众多影响因素，且没有统一的量纲.为了能够较全面考虑各因素且简化模型，将众多影响因素转化为关键指标隧道半径、坡度、能见度和路面摩擦系数进一步分析，构建最佳速度模糊控制系统，得出隧道通行的最佳速度，并将该速度作为元胞自动机模型的最大速度，即隧道的限速.最后根据隧道不同区段交通流特征，对行车规则和元胞自动机模型参数进行改进，建立一种适用于高速公路特长隧道的交通流元胞自动机模型，分析研究车辆行驶在隧道不同路段时的加速、减速等微观交通现象.

1 高速公路特长隧道交通特征分析

JTG D70—2004《公路隧道设计规范》[13]中按照长度将公路隧道分为短、中、长、特长隧道4类.特长隧道指长度L>3 000 m的隧道.高速公路特长隧道交通流具有封闭性、动态性和相对独立性，受道路条件、环境状况与驾驶员特性综合影响.

1.1 道路条件

车辆在隧道行驶过程中，弯道和纵坡直接制约车辆行驶状态.若行驶不当，车辆易在弯道处产生侧滑与倾翻，此外，车辆在坡道处也频发事故.弯道和纵坡的主要衡量指标分别为半径和坡度.

1.2 环境状况

隧道空间相对比较封闭，影响其交通流状况的环境因素主要有：空气污染物、天气、照度和路面材料.空气污染物，雨、雪、雾等天气不仅导致隧道内能见度低，影响行车视距，还影响路面摩擦系数；此外，路面材料直接影响路面摩擦系数，以及与照度共同对隧道内能见度产生直接影响.因此，环境对隧道内交通流状态的影响主要体现在能见度和摩擦系数上.

1.3 驾驶员视觉特性

特长隧道通常需要人工照明设施来保障隧道内的照明.车辆在进出隧道时，驾驶员需要在自然光照射区域和人工照明区域之间进行切换，产生照明差异.车辆在特长隧道不同路段的行驶过程中，会产生不同的视觉体验[14].

1)黑洞效应 车辆驶近特长隧道时，隧道内亮度较低，驾驶员无法详细观察隧道内环境状况，视觉上洞口如“黑洞”一般，无法看清洞口附近的情况.因此，驾驶员会在进入隧道之前减速行驶，将速度降到相对较低的范围.

2)暗适应 当驾驶员进入隧道后，视觉不能迅速适应亮度的突然降低，产生“暗适应”现象，导致视觉滞后.为安全起见，驾驶员在刚进入隧道的时候仍然会保持相对的低速.

3)白洞现象 隧道外部亮度远高于内部亮度，驾驶员驶离隧道时，从暗环境出，瞬间会感到光线刺眼发眩，很难看清外界事物，即“白洞现象”.此时，驾驶员往往会减速行驶.

4)明适应 车辆由隧道暗处行驶到亮处，“白洞现象”出现，驾驶员往往需要几秒钟或几分钟适应当前环境，之后逐渐看清物品，这叫“明适应”，往往外部光的强度越强，“明适应”的时间也就越长.车辆明适应阶段，驾驶员调整驾驶行为，逐渐提速.

2 特长隧道区段划分

车辆在特长隧道的不同区段行驶过程中会产生不同的视觉效应.车辆进入特长隧道前为引入区段，特长隧道区段可分为4段：入口段、渐变段、基本段和出口段，参照文献[13]对各区段长度的计算如下.

车辆进入隧道后为速度调整段.因隧道区域照明不充分，驾驶员往往无法准确辨识洞口情况，常以较低速度进入引入段.进入隧道时，驾驶员不能迅速适应隧道内亮度，易产生“暗适应”，仍保持相对低速.入口段长度Dth：

(1)

式中：Ds为照明停车视距；h为洞内净空高度.驶过入口段，驾驶员视觉逐渐适应特长隧道内环境，逐渐提速到隧道限速附近.渐变段长度：

Dtr=Dtr1+Dtr2+Dtr3

(2)

式中：Dtri为渐变段i的长度，m；Dtr为渐变段长度；V为隧道限速.在此区段行驶过程中，车辆按照驾驶员期望行驶速度前行，车速相对平稳；当车辆即将驶出隧道，由于内外部亮度相差较大，易产生“白洞”现象，驾驶员开始制动，降速行驶至离开隧道.单向交通隧道中的出口段长度宜取60 m，即剩余为隧道基本段长度.

通过以上分析，特长隧道区段划分及车速大致空间变化见图1.

图1 隧道车速空间变化示意图

3 基于元胞自动机的交通流模型

3.1 基于模糊控制系统确定车辆最佳限速

车辆最佳限速(km/h)与特长隧道内能见度(m)、摩擦系数、弯道半径(m)、纵坡坡度值(%)相关，从而建立图2的两层模糊决策结构来确定最佳限速值，各参数论域与模糊语言值见表1，其隶属函数分布见图3，各指标系统采用Mamdani型推理规则.

图2 模糊控制系统

表1 参数的论域及模糊语言值

图3 隶属度函数

1)行车环境模糊规则库 根据能见度和摩擦系数进行模糊控制的模糊规则：

If(x1isAi)and(x2isBj), Then,(xisCq)

i,j,q=1,2,3,4,5

(3)

当能见度与摩擦系数较差，行车环境也较差，改善能见度和摩擦系数的取值，行车环境的取值变好，当能见度和摩擦系数取值最佳时，行车环境达到最优.

2)道路线形模糊规则库 根据弯道和纵坡进行模糊控制的模糊规则：

If(y1isRi)and(y2isFj), Then,(yisKq)

i=1,2,3；j=1,2,3；q=1,2,3,4,5

(4)

当转弯半径为急弯，坡度为陡坡时，道路线形属于差范围内，随着转弯半径和坡度变缓，道路线形的所属范围变好，当转弯半径与坡度均较缓时，道路线形取值很好.

3)最佳速度模糊规则库 根据行车环境和道路线形进行模糊控制的模糊规则：

If(xisCi)and(yisKj), Then,(zisDq)

i,j,q=1,2,3,4,5

(5)

最佳限速的范围在行车环境和道路线形很差时属于很低，随着行车环境和道路线形取值变好，最佳限速的取值提高，直到两者取值都为很好时，最佳速度取值很高，见图4.

图4 模糊推理系统输出曲面

3.2 特长隧道元胞自动机模型构建

以特长隧道入口为起点，出口为终点，车辆的到达具有随机性，采用开放性边界条件，车辆到达服从泊松分布.

(6)

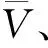
步骤1最大运行速度

Vmax=Vp

(7)

式中:Vp为最佳运行速度.

步骤2加、减速度

1)最大减速度 特长隧道内路面摩擦系数因环境影响往往比普通道路小，即车辆最大减速度变小，取值3 m/s2.

2)最大加速度 车辆在特长隧道内行驶，由于能见度低，加速度要比隧道外小，取值3 m/s2.

步骤3更新规则

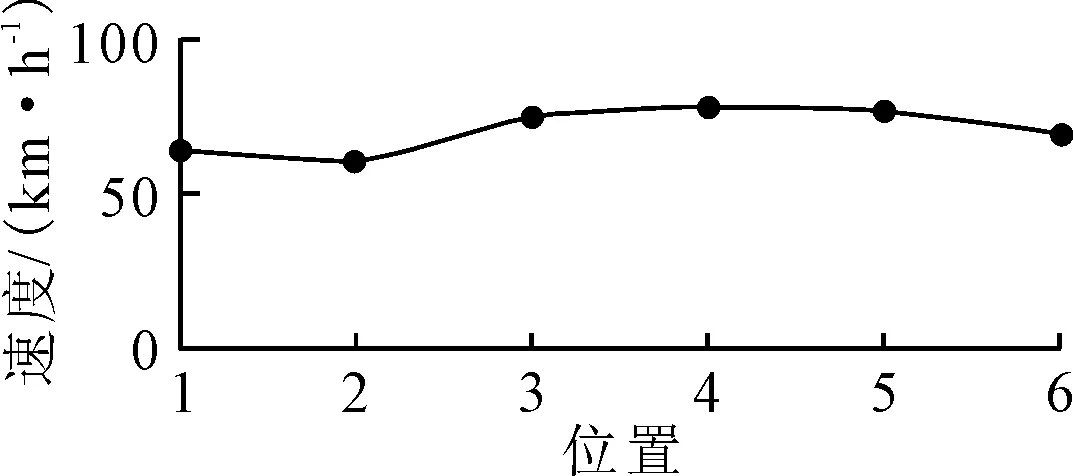
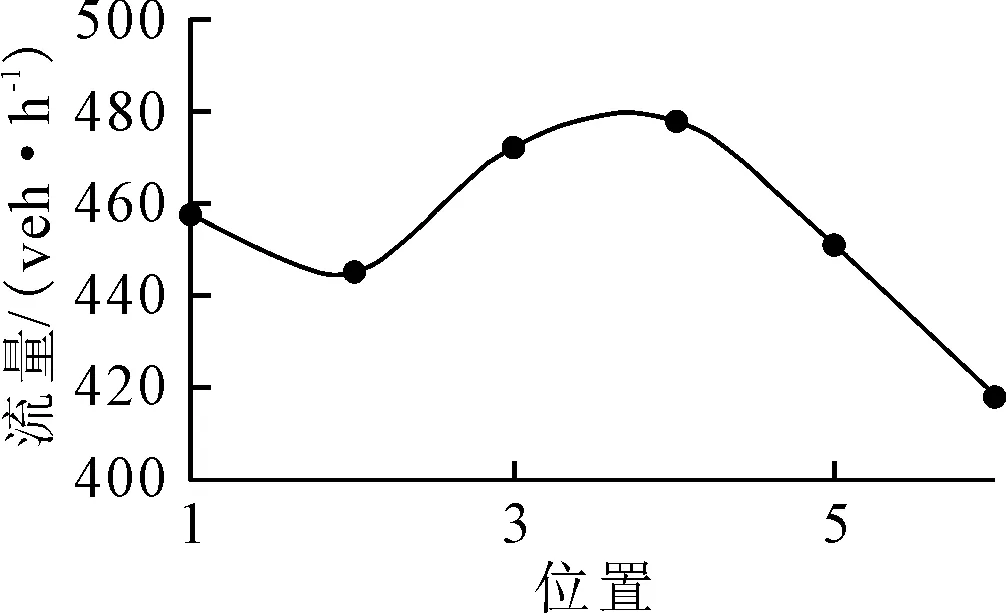
1)减速 if[(xn(t)

if[rand()]

max{(Vn(t)-β1),dn}

当车辆进入车道时间小于驾驶员“暗适应”时间时，认为车辆处于入口段，车辆以p1的概率进行减速，减速度为β1.

2)加速 if[S2

if[rand()]

min{(Vn(t)+α)，Vmax}

车辆处于渐变段和基本段时，驾驶员尽量以最大速度行驶.

3)随机慢化 if[rand()]

随机慢化体现在驾驶员行为差异，隧道内不能临时停车，因此设置速度下限Vmin(由最低限速确定).

4)安全刹车Vn(t+1)=min{Vn(t),dn}；dn=xn+1-xn-l

当车辆行车间距太小时，后车需减速.将安全刹车置于随机减速后，能较好地控制车辆随机减速结果.

5)位置更新xn(t+1)=xn(t)+Vn(t)

6)换道规则

dndn；

dneighbor,back>db；rand()

第一条为车辆在本车道上不能按规定的速度行驶；第二条为旁道行驶条件优于本车道；第三条为确保车辆n和旁道后车间保持安全距离，通常取db=Vmax；第四条为当满足换到条件时，驾驶员以概率Pchange进行换道.Vn(t+1)为t+1时刻第n辆车的速度；Vn(t)为t时刻第n辆车的速度；xn(t)为t时刻第n辆车的位置；xn(t+1)为t+1时刻第n辆车的位置；tn为第n辆车所执行时的时步数；t0为暗适应时间；β1为车辆在入口段的减速度；β2为车辆在其他区段的减速度；A为车辆加速度；dn为第n辆车和前车的距离；L为车辆长度.

针对隧道不同区段，所建立的特长隧道元胞自动机模型除了随机慢化和安全减速外，在入口和出口区段增加了减速规则且大于随机慢化的减速度，加速规则只发生在渐变段和基本段.对于整个隧道而言，各个变换规则的概率取值不同于普通路段取值，因驾驶员在特长隧道心理紧张，随机慢化概率大于普通路段；驾驶员在出入隧道时，因视觉变化会频繁制动，有较大的减速概率；当进入渐变段，驾驶员已适应隧道环境，为使车辆以最大速度行驶，开始频繁加速，加速概率要大于隧道外部区段，具体示意图见图5.

图5 特长隧道不同区段的变换规则

4 案例分析

以隧道进口里程K58+725，出口里程K64+827，总长度为6 102 m的西汉高速某特长隧道上行方向为研究对象.通过各区段长度公式，确定该隧道入口段长度96 m，渐变段315 m，出口段60 m，基本段长度为5 631 m.隧道内部从入口方向到出口方向设有6个检测器,见图6.

图6 数据采集点示意图

4.1 实际交通流特性分析

1)速度特性 对上行方向的6个数据采集点进行地点车速平均值计算，结果见图7.由图7可知：车辆驶入隧道速度下降，位置2之后车速开始提升并保持在一个速度范围，在接近隧道出口处，车速开始下降，直至车辆离开隧道.

图7 隧道内位置-速度示意图

2)流量特性 图8为不同位置小时流量，由图8可知：特长隧道中间段单位时间流量最大，其次为进口段，出口段的单位时间流量整体偏小.这与驾驶人在特长隧道中间段逐渐适应隧道环境，而在隧道出口段受明适应及眩光影响较明显相关.

图8 不同位置小时流量

3)车头时距 车头时距是交通流的一个重要参数，描述交通流前后相邻两辆车的前端通过某同一地点的时间差.车流密度和速度影响车头间距分布，在中高密状态，速度对密度的改变相当敏感，且速度对于确定车头间距至关重要.图9为采集点1～6车头时距分布图.

由图9可知：采集点2、4、5、6处的车头数据频率分布类似，0～10 s的区间频率最高.而采集点1频率最高的区间为20～30 s，采集点3频率最高的区间为10～20 s.为进一步分析各区段的车头时距特性，求得其平均值和方差见表2.

表2 车头时距分布

图9 采集点1～6车头时距分布图

由于采集点2、5和6的方差最大，说明这几点交通流稳定性低，交通流波动较大.

4.2 模型仿真

4.2.1参数选取

结合秦岭隧道的实际环境，定义相关参数.

1)隧道内各区段长度 入口段长度96 m，渐变段315 m，出口段60 m，基本段长度为5 631 m.

2)元胞长度 一般来说，取元胞长度为7.5 m，但其加、减速度最小只能是7.5 m/s2，不符合隧道实际情况.即取元胞长度为1.5 m.

3)边界条件 取开放性边界条件，当头车的位置大于等于隧道出口的位置，则该车辆离开系统，入口处车辆按照泊松分布到达，车辆到达率是0.5辆/s.

4)最佳限速计算 测量隧道内能见度为300 m.隧道内路面摩擦系数为0.5.最困难路段的坡度和转弯半径，分别为-3%和3 300 m.

用MATLAB模糊控制工具箱进行仿真计算，输入参数计算得到最佳限速：Vmax=85 km/h，以此作为元胞自动机的Vmax，得到指标模糊规则仿真图，限于篇幅，图略.

5)选取加速度α、减速度β1，β2在入口段和出口段，因为暗适应和明适应的作用，减速度要大于随机慢化的减速度，取最大值β1=3 m/s2,在其他区段的减速度取β2=1.5 m/s2.驾驶员在低能见度行驶时，通常警惕性比较高，因此车辆加速度α要比隧道外小，取α=1.5 m/s2.

6)车辆初始速度 为了保证车辆在进入特长隧道时，速度满足隧道限速的要求，取车辆进入隧道的初始速度为隧道的最佳限速，即85 km/h.

7)随机慢化概率 由于驾驶员警惕性比洞外高，因此随机慢化概率较高，取p=0.25.

8)换道概率 在隧道内车辆换道的概率较小，取Pchange=0.1.

具体仿真流程见图10.

图10 特长隧道元胞自动机模型仿真流程图

4.2.2仿真结果分析

1)位置-速度图分析 隧道口处，规定车辆进入隧道的限速为16元胞/时步.图11为隧道内不同位置的平均速度，由图11可知：入口段、出口段处驾驶员需要适应视觉特性变化，往往车辆速度快速下降，渐变段，车辆适应当前行驶环境，逐渐提速至接近最佳限速，到达基本段，车辆运行平稳，接近最佳限速值，并在固定区间范围内波动，由此可见该模型仿真结果与该特长隧道交通流实际速度特性相符.

图11 隧道内不同位置的平均速度

2)时空图分析 固定各区段加减速度及其概率、随机慢化概率等参数，最佳限速调整为12元胞/时步，泊松分布中车辆到达率设为0.7辆/s，仿真结果见图12.

图12 时空图

由图12可知：当车辆开始驶向特长隧道，速度变小，车流量较大时在入口段处车辆产生排队拥堵，并极大可能对渐变段产生影响，基本段和出口段处车辆相对比较稳定.相比其他区段，入口段的通行能力最低.此外，出口段的平均车速也较低，却无严重交通拥堵状况，主要因为入口段的到达率高于出口段.

3)基本图分析 图13为隧道4个区段的密度-流量曲线图和密度-速度曲线图.

图13 四个区段的密度-流量和密度-速度图

由图13可知，特长隧道各区段流量与密度紧密相关，起初，随着密度增加，各区段车流量以及车流量的增长速度增加：入口段<出口段<渐变段<基本段.当车流密度达到某临界值时：入口段>出口段>渐变段>基本段，各区段车流量均下降且满足：基本段>渐变段>出口段>入口段，即各区段通过能力：入口段>出口段>渐变段>基本段.后期，当车流密度不断变大，各区段车辆的行驶速度均比较低，即表明密度极大时，隧道内发生拥堵，此时，各区段的密度-流量曲线和密度-速度曲线均重合.因此特长隧道各区段自由流阶段的交通流特性差异较大.

车辆行驶的自由流阶段，因各区段的平均车速有所不同，导致同一车流密度下各区段的流量关系为：基本段>渐变段>出口段>入口段.车速越高，相应的车流量越大.各区段车辆速度相同时，各区段车流密度关系为：基本段>渐变段>出口段>入口段.一般情况下，车流密度小则相应的车速越大，此规律与图中数据不同，主要是因为车速还与各区段的行车环境相关，特长隧道的渐变段阶段往往车速较低，出口段比入口段视觉适应时间长，相比下，行车环境：基本段>渐变段>出口段>入口段，基本段的行车环境最优.

综上，该模型仿真结果与该隧道实际交通流特性较相符，并且可较好地揭示出驾驶人、车辆、道路、环境条件等因素以及它们之间的相互影响和联系.

5 结 束 语

以交通流理论为基础，构建了一种基于模糊逻辑算法的特长隧道元胞自动机模型.分析了特长隧道的道路线形、环境状况、驾驶人特性等特征，以能见度、摩擦系数、坡度和转弯半径作为输入变量，建立两层模糊逻辑控制结构，通过建立合理的模糊规则库，运用MATLAB中的模糊控制器进行仿真模拟，输出最佳限速值，用于修正元胞自动机模型中的最大速度.根据驾驶人在隧道不同位置的视觉特性，在隧道不同区段设置了不同的变换规则，并确定了相关参数.仿真案例结果表明，该模型所描述特长隧道内的交通流特征与实测数据所体现出来的隧道交通流特征相符.