Parallel-Dynamic Interpolation Algorithm of Sea Surface Height for Future 2D Altimetry Mapping of Sea Surface Height

DI Jiankai, MA Chunyong, 2), *, and CHEN Ge, 2)

Parallel-Dynamic Interpolation Algorithm of Sea Surface Height for Future 2D Altimetry Mapping of Sea Surface Height

DI Jiankai1), MA Chunyong1), 2), *, and CHEN Ge1), 2)

1),,266100,2),,,266237,

The sea surface height data volume of the future wide-swath two-dimensional (2D) altimetric satellite is thousands of times greater than that of nadir altimetric satellites. The time complexity of the 2D altimetry mapping reaches O(3). It is challenging to map the global grid products of future 2D altimetric satellites. In this study, to improve the efficiency of global data mapping, a new algorithm called parallel-dynamic interpolation (PA-DI) was designed. Through the use of 2D data segmentation and fine-grained data mosaic methods, the parallel along-track DI processes were accelerated, and a fast and efficient spatial-temporal high-resolution and low-error enhanced mapping method was obtained. As determined from a comparison of the single-threaded DI with the PA-DI, the new algorithm optimized the time complexity from O(3) to O(3/), which improved the mapping efficiency and achieved the expected results. According to the test results of the observing system simulation experiments, the PA-DI algorithm may provide an efficient and reliable method for future wide-swath 2D altimetric satellite mapping.

parallel computation; data segmentation; data mosaic; dynamic interpolation; wide-swath 2D altimetric satellite

1 Introduction

Great contributions have been made by the nadir alti- metric satellites in the past thirty years. Among the nadir altimetric satellites include the ERS-1/2 series satellite, Environmental Satellite (EnviSat), and TOPEX/Poseidon (T/P)/Jason series satellite (Mather., 1979; Amores., 2018). Since the objective analysis method (Bretherton., 1976) was proposed, most of the sea sur- face height (SSH) grid data products, including AVISO (Ar- chiving, Verification, and Interpretation of data of Satellites Oceanography) maps (Martin, 2014; AVISO, 2019), are always based on interpolation algorithms with predefined spatial-temporal covariance models (Chelton., 1998). The optimal interpolation (OI) algorithm is the most popular altimetry data mapping algorithm for ocean remote sensing (Le Traon., 2003). In 1998, Le Traon. (1998) tried to solve the long-wavelength error (ELW) during oceanographic satellite mapping and found out that ELWcould be reduced from cross-track OI, which will improve the mapping performance of altimetric satellites. In addition, Le Traon. (2003) first introduced a mul-ti-satellite combined observation data mapping method, which effectively promoted the spatial resolution and data accuracy of altimetry mapping. Moreover,Dussurget. (2011) improved the OI algorithm to implement data mapping products in fine resolution to observe mesoscale ocean dynamics phenomena (Dussurget., 2011; Morrow and Le Traon, 2012).

Amores. (2018) utilized the OI method with traditional altimeter satellite along-track sampling data to map the SSH in the Mediterranean Sea and other regions, and the OI method based on combined observation from multi- satellite altimetry data product could only observe 6%–16% of the ocean dynamic phenomena occurring in the ocean. In 2020, Ma. (2020) utilized the OI mapping method with surface water and ocean topography (SWOT) satellite parameters to conduct observing system simulation experiments (OSSEs) in the Kuroshio Extension (SouthChina Sea) region. The result illustrated that more than 60% of ocean dynamic phenomena could be observed in the SSH grid data.

The OI algorithm is a statistical, static interpolation te- chnique (Morrow., 2019), through which the meso- scale ocean phenomena can be observed from the global mapping products.However, the OI method has some li- mitations in terms of error reduction and resolution improvement in mapping practices. To improve the time re- solution of mapping and observe and analyze phenomena smaller than the mesoscale, a mapping method based on the theory of physical oceanography has been introduced. Ubelmann. (2015) mentioned the problem of insufficient time resolution of altimetric satellites. To solve the problem, a dynamic interpolation (DI) method based on the potential vorticity (PV) conservation theory (Pedlosky and Leibovich, 1987) has been proposed. Ubelmann. (2016) used the method described above, combining DI with computer technologies such as Kalman filter, and performed the DI of the combined observation from three satellites altimetry data. The DI method has also been gra- dually integrated into products by AVISO (CNES, 2016). Morrow. (2019) introduced the DI based on the theory of PV conservation and applied it to the mapping of wide-swath 2D altimetric satellites (WSAS) along-track sampling data onto energetic western boundary currents sea region. Compared with the OI method, the perfor- mance of the DI method achieved a 30% error reduction rate in the observation capability of dynamic ocean phenomena and a 20% resolution improvement rate (Ubelmann., 2016; Morrow., 2019).

As one of the advanced mapping methods, DI will also be used in mapping products of WSAS in the future, including the SWOT mission (Fu and Ferrari, 2008; Gaul- tier., 2016; Morrow., 2019) and the Guanlan mission (Chen., 2019) (a future ocean scientific sa- tellite mission of China). Owing to the characteristics of a large volume of satellite altimetry data, continuous sate- llite data accumulation due to revisiting, and multiple sa- tellite altimeter missions, the inclusion of parallel computation and processing in the mapping is crucial, including existing and planned altimetry sensors. However, when DI is applied on 2D along-track SSH data for future WSAS, the time complexity of the algorithm may reach O(3), as described in Section 3. Furthermore, the data volume of WSAS is approximately 5 terabytes (TB) @ 1km×1kmresolution (Fu and Rodriguez, 2004), which was foundthrough the OSSEs for WSAS (21-day cycle for SWOT or 14-day cycle for Guanlan). The along-track SSH data of nadir altimetric satellites were almost always one-dimen- sional (1D) data, and the data volume was not very large (even that of the combined observation data of three or four satellites). Taking the Jason-2 sampled data as an example, the per 30-day global cycle data volume was only 800 megabytes (MB) (Chavanne and Klein, 2010). In com- paring the sampled data dimensions, data size, and computing the time complexity between WSAS and nadir al- timetric satellites, using the DI mapping method on WSAS could be much less efficient than using nadir altimetric satellites, which results in challenges for data mapping of the future WSAS.

Focusing on improving the mapping efficiency for WSAS, this paper provides a PA-DI method based on the PV conservation theory and presents the simulation of the SSH data of the WSAS.

To promote the data-processing performance, using region partitioning technology (Liu., 2016) and combining parallel computing methods with higher core numbers (KerrAaron., 2013; Tang., 2018) will be an appropriate approach. However, the result of the data mo- saic method will vary according to the different usages for ocean remote sensing, oceanographic or geographic, and the data mosaic technique will be the key factor of the region partitioning. Through 2D data segmentation and fine-grained data mosaic methods, the utilization of CPU cores (K) and the spatial-temporal data-partition number (L), the PA-DI algorithm optimized the time complexity of SSH data mapping, reducing it from O(3) to O(3/). (For more details on the determination of the,, andof the O(3/), see Sections 3 and 4) Through the experiments, the new algorithm could significantly improve the operational efficiency.

The remainder of this paper is organized as follows: Section 2 introduces the materials used for the OSSEs, in- cluding the Guanlan satellite orbit parameters and the OSSEs.Section 3 systematically introduces the PA-DI method. Sec-tion 4 presents the results and discussions. Finally, in Section 5, the conclusions and future works are discussed.

2 Materials

In this study, the main materials used for the OSSEs are as follows:

i) The Guanlan satellite orbit parameters, which are used to implement the OSSEs of the WSAS for mapping. These parameters are presented in Table 1. The orbit altitude of the Guanlan satellite will mainly meet the requi- rements of dual-load observing mission tasks conducted si- multaneously (Chen., 2019).As parameters for gene- rating the input sources of the OSSEs, the exact repeat cycle, the sub-cycle, the orbit altitude, and the swath width are required in the calculation process of the along-track sampling simulations. In the experiment, the Orbit 2 column in Table 1 was used. Using the parameters of this satellite for sampling simulation will meet the requirements of prac- tical application for WSAS in the future.

Table 1 provides two-orbit schemes involving three- month Fast-sampling orbits. The altitude of Orbit 2 is 791.254km, which ensures a high observation swath of the WSAS and provides the parameters for the OSSEs of the Oregon subregion and the Hybrid Coordinate Ocean Model (HYCOM). The exact repeat cycle of Orbit 2 is approximately 14d (4-day sub-cycle), with a swath width of 166.4km. A sub-cycle is an integer number of days after which the ground track of a satellite repeats itself within a small offset. In other words, a sub-cycle can be viewed as a near-repeat cycle with a duration equal to an integer num- ber of nodal days (Pie and Schutz, 2008). Utilizing these parameters, the OSSE results will be used as input data for mapping, which will be systematically described in Sections 3 and 4.

ii) The SWOT simulator dataset of the Oregon-region (aregion of the Oregon coast (Gaultier., 2016a, 2016b)) model in 2016, which is used to test the PA-DI applicabi- lity described in Section 4. The SWOT simulator is the SWOT sampling simulation and error analysis simulation platform designed by the SWOT scientific research team. The data resolution is high, and the Oregon-region is suitable to facilitate the rapid iterative verification of the algorithm. Furthermore, the SWOT simulator data have been verified and approved by the relevant WSAS scientific research. The SWOT simulator dataset is the authoritative high-precision grid data provided by the SWOT simulator team; it is combined with several mainstream model datasets and has a resolution of 1km×1km. This dataset can provide a more realistic application scenario for the along- track sampling simulation of WSAS like the SWOT (Durand., 2010; Ubelmann., 2014).

Table 1 Guanlan satellite’s orbit parameters

The grid data of the SWOT simulator dataset in the 100-day Oregon-region begin with the OREGON-0100 file and end with the OREGON-0199 file. These data simulated the high-resolution grid dataset (up to 1km×1km) in the 4.5˚×5.5˚ region of Oregon (124˚–130˚W, 42˚–48˚N). This dataset includes one private NETCDF FORMAT_ MODEL (netCDF, network Common Data Form) and four main models: ROMS, NEMO, MITGCM, and CLS_ MODEL. The development team of this dataset has also created a SWOT simulator software processing environment, which includes examples of SSH data mapping simulation of KaRIN and many errors (including KaRIN instrument errors based on phase, roll or baseline errors, noise error, wet_tropo error, SSH error, and other systematic errors) and their respective correction technologies (Gaultier., 2017; Peral and Esteban-Femandez, 2018). The main four high-resolution ocean general circulationmodel data, ROMS, NEMO, MITGCM, and CLS_ MODEL (Mohamed., 2004; Forget., 2015; Vidard., 2015), are used for the Oregon-region dynamical simulation in the SWOT simulator model library for user optional preferences selection, which could be utilized for the SSH simulation function and surface fluxes,up-stream, and oceanic dynamical phenomenon simulation.

In this study, the SWOT simulator was not directly used to process the SSH data in the test environment. However, the grid data of the dataset (@ 1km×1km resolution) were used as the analysis object to perform the OSSEs.

iii) The HYCOM data (from 2013 to 2018), which were used to evaluate the SSH data mapping results (Section 4). For instance, after the data mapping evaluation of the cor- responding DI algorithm, the results were compared with HYCOM original data. The HYCOM data cover the global region, which is conducive to implementing the mapping simulation works in different target sea regions. The HYCOM data are updated annually and made available to the public, and they are representative model data in the application of OSSEs, which facilitates scientific research and the mutual verification of peer work. Furthermore, the HYCOM is a part of the Global Ocean Data Assimilation Experiment of the United States (Halliwell and Wallcraft, 2018). HYCOM aims to develop and evaluate coordinated ocean models (generalized). HYCOM real-time high-resolution model includes three-dimensional (3D) ocean-state description, local coastal model, and global coupled ocean-atmosphere prediction model with prescri- bed ocean boundary. HYCOM data adopt the global 1/12˚× 1/12˚ resolution analysis model output from the U.S. Navy Global Backward Projection Experiment Ocean Model, and the resolutions of some individual local regions can reach 1/25˚×1/25˚. The HYCOM data are one of the po- pular mixed models.

3 Methodology

The calculation process of DI mapping requires background knowledge of physical oceanography parameters, such as velocity field, relative vorticity, and PV (Fu and Flierl, 1980; Pedlosky and Leibovich, 1987; Lapeyre and Klein, 2008). In this paper, the related knowledge of physical oceanography or geophysical fluid dynamics could re- fer to the following books,., Pedlosky and Leibovich, 1987; Wunsch, 1996; Lapeyre and Klein, 2008. The following parallel computing algorithm was designed to improve data mapping efficiency.

Fig.1 describes the implementation process of the PA- DI algorithm, including the use of spatial-temporal DI data mapping and Green’s Function to calculate the DI in the frequency domain and the use of Kalman filter (Fukumori, 2002) to generate the global grid data of the WSAS.

If we define the 2D SSH data asX×Y, and define the 1D time parameters asT,when DI is utilized through a single thread for WSAS, the 2D spatial SSH data and 1D temporal parameters could be calculated asX×Y×T, which makes the time complexity of the algorithm reach O(3) during the search for data in the global observation space (represents the searching depth, the range ofis from 1 to,Î).

The whole software architecture of PA-DI is divided into two parts: parallel part and sequential execution part. The parallel part includes along-track sampling simulation on OSSEs, data segmentation, and DI calculation (see the blue dotted area for details), while the sequential execution parts are the processing of the along-track sampled data of WSAS; the use of data mosaic; the use of Kalman filter and its follow-up processes, such as the data verification, data analysis, data comparison, and the sea level anomalies (SLA) calculation.

Fig.1 Block diagram of PA-DI algorithmic implementation processes.

The production of ocean science satellite mapping will be mainly based on observation data collected by satellite. The sampling simulation is the theoretical pretesting pro- cess before the WSAS launch. According to the orbit of the Guanlan satellite and its parameters, the swath width, the nadir gap width, the coordinates of the swath trajectory and the gap trajectory of the satellite had been calculated. Then, combined with the OSSEs, the sampled data in one cycle were merged to generate global observations, which will be used as the input source data for the subsequent mapping process. In the OSSEs, the data of each orbit on each cycle are calculated by the satellite track ana- lysis algorithms using reasonably matched satellite para- meters, which are implemented under multi-core paralle- lized methods.

Parallel computing includes the parallelization of computing technology, numerical algorithm, and processingequipment (or computer) structure. Parallel processing in- volves dividing large data and numerical computing tasks into several independent and simultaneous subtasks and coordinating these subtasks to achieve a fast and efficient solution to a given problem (Lguensat, 2019). From the perspective of abstract instructions and data processing structures, parallel computing technologies include thefollowing: the Single Instruction and Single Data (SISD), the Single Instruction, Single Data and Multiple Data (SIMD), the Multiple Instruction, Multiple Data and Single Data (MISD), the Multiple instruction and Multiple data (MIMD) (Cormen., 2009).

To evaluate the performance of parallel algorithms, a quantitative index based on computational time can be used, the indicators of which mainly include acceleration, efficiency, and communication calculation ratio (Roosta, 2000; Cormen., 2009; Melab., 2018). The acce- leration is based on the comparison of the execution time between a single processor and multiple processors (Eq. (1)).

1represents the execution time of sequential algorithms (that is, on a single processor), andTis the execution time of a parallel algorithm.

The DI method is on the basis of PV conservation and is parallelized in this study. Data exchanges and allocations are working all the time. The detailed block diagram of the software architecture is illustrated in Fig.2.

The left part of Fig.2 shows the theory and methodology flow of the PA-DI algorithm, while the right part illustrates the architecture and data streams running in the software. According to the number of CPU cores within a given computer, the number and size of global or regional data segmentations are arranged and reformatted into data formats that meet the requirements of parallel computing. The following section describes each detailed step of the PA-DI algorithm.

3.1 Data Segmentation

If we define theth subregion of data segmentation asX×Yformats (the range ofis from 1 to,Î), the number of CPU cores as, and data partitions number as, so thatX≈X, Y≈Y, then the formulaX×Y×Tof space-time will be described as follows:

Then, the time complexity of the PA-DI algorithm is reduced from O(n3) to O(n3/KL), and the whole calculation process will be accelerated.

Fig.3 Illustration of the data segmentation step: (a), sketch of the method; (b), experimental schematic (the north tropical region in the West Pacific Ocean, WPO).

As shown in Fig.3, the target region can be divided intodata partitions; for example, the north tropical region in the West Pacific Ocean (WPO) region is divided into more than eight data partitions (on the left part of Fig.3b), and one of the partitions is the range of 160˚E to 170˚E latitude (on the right part of Fig.3b), and this data will be in- putted into the next step for implementing the parallel-DI processes.

In the experiment, the priority is to ensure that the sub- mesoscale and mesoscale ocean phenomena are retained during data segmentation, and that the ocean phenomena conform to scientific rules in the implementation of the data mosaic. Thevalue is the number of areas divided, which should be implemented based on the above basic premise. It is necessary to preserve the ocean phenomenon and ensure improved efficiency. Ifis too large, the block will be too small, which will lead to the risk of losing the target ocean phenomenon; ifis too small, the partitioned area will exceed the memory limit. When≥, parallel operations can be fully utilized, andshould be designed to satisfy an integer multiple ofas much as possible. Moreover, the choice of parameterdepends on the hardware resources provided by the computer, and the greater thevalue, the better. The number of processes in the program should be ≤; the number of processes and the degree of operation acceleration are linearly related. If the number of processes is greater than, the computing performance will not be significantly improved, and the waiting queues will also increase, which will increase the overall scheduling time and reduce the computing efficiency.

According to the satellite parameters, the along-track sampling simulation was performed. Each cycle of the along-track sampled data of WSAS was based on the la- titude and longitude coordinates of 2D high-density data, which can be defined asX×Y, as already mentioned above.From a data processing perspective, the sampled data could be considered as a 2D data space; therefore, during the data mapping implementation, due to the direct calculation data volume being too large, the 2D data segmentation method was adopted, and the WSAS sampled data of each cycle for processing was divided into 400 positions, 600 positions, 800 positions, or 1000 positions, which would be described inX×Yformats. For details of the subregions of the 2D data segmentation, see Figs.2 and 3, the subregions block part.

3.2 Dynamic Interpolation Calculation

In 1996, Wunsch and Carl. (1996) elaborated on the definitions of vorticity and PV and introduced the PV conservation as follows:

whereis the current function,(, ) is the Jacobian ma- trix,Ñ2is the Laplacian operator, andis the integral time; then,

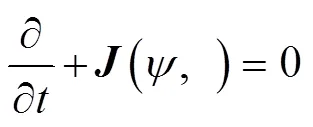
and

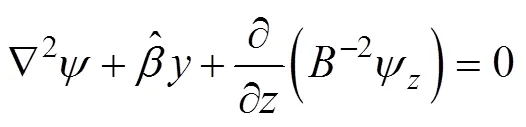
whereis the platform function,is the current function, and−2is the V-N formulation.

Regarding the observation space of the satellite remote sensing, the temporal resolution of WSAS probably would be unmatched with the high spatial resolution itself due to the character of the satellite orbits (Ubelmann., 2015). Therefore, the main scope of the DI algorithm is to improve the grid data mapping resolution of WSAS, both in time and space. The basic preliminary theory of the DI al- gorithm is to use geostrophic velocity to perform the active advection of PV and calculate the SSH from a known observation field, with iteration at each time step. Therefore, the data of the WSAS will be dynamically iterated from 3D space-time (2D space, 1D time), so that the re- solution of time and space resolutions can reach the high quality required for scientific research (Ubelmann., 2016). The general implementation process of the DI algorithm can be summarized as follows. Within a given time period, the SSH data are used to initialize PV theusing the following equations:

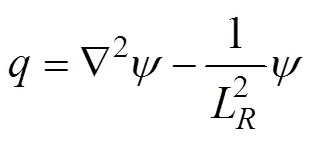
and

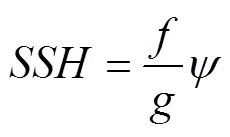
whereÑ2is the divergence of the gradient of the 2D field vector,., the horizontal 2D Laplacian operator;is the integral time;Lis the first Rossby deformation radius;is the gravity constant; andis the Coriolis parameter. The first Rossby deformation radius corresponds to one of the simulation results: L=25km. This is a typical value for oceans in mid-latitudes (Chelton., 1998; For- get., 2015). Then, at each time step, the current functionis iteratively computed using Eqs. (6) and (7), and thevalue is continuously updated during the iteration process. The iteration process adds the specific boundary conditions mentioned above and converges after the iteration. Moreover, during the whole process, DI SSH, the updated SSH after iteration, is given by equation

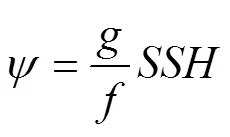
or Eq. (8).

The SSH initial matrix of the above process can be defined as follows: to merge the original SSH observation data (or SLA data), the objective analysis and the Kalman filter methods will be used (Ubelmann., 2016). Corresponding to the Kalman filter gain, taking the SSH data for instance, the formula of the input matrix can be expressed as follows:

To conform more to the true observation (., the mea- surement errors), a small perturbation parameter(., mm-level perturbation) is added randomly in the calculation process (Le Traon., 1998). In Eq. (9),is the interpolation SSH value of the target location in the whole grid mapping space,observeis the SSH value of observation space,(observe) is the covariance coefficient matrix(the observation operator) multiplied byobserve,is a matrix of small perturbation parameters, and(observe)+is the matrix of the true observed values.

The along-track SSH data were used as the input matrix of Eq. (9), with separate trajectories during each single circle of the cycle (an up track and a down track in one circle), and the SSH grid data after final mapping were produced by the Kalman filter described above.

Eq. (9) combines the method of conjugate gradient algorithm and uses the combination form of the Kalman filter to map the SSH data in the 3D field (1D temporal and 2D spatial). Through multi-core parallelized methods, the data will be reconstructed in space and time, containing certain ocean science information.

Considering the purpose of observation from the WSAS, some interesting wavelengths could be more important than others, for instance, from 15km to 150km. After the SSH initial matrix is obtained through multi-core parallelization, using the Green’s function method could help reduce the calculation scale and streamline the wavelengths to the more targeted ones, which transforms the altimetry data from the time domain to the frequency domain by 2D Fourier transform. In the case of a finite range of wave- lengths, it is possible to consider only the linear response of a finite number of modes (Ubelmann., 2016).

Eqs. (10) and (11) are the implementation equations of the Green’s function method:

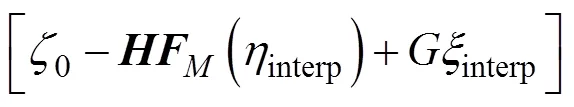
and

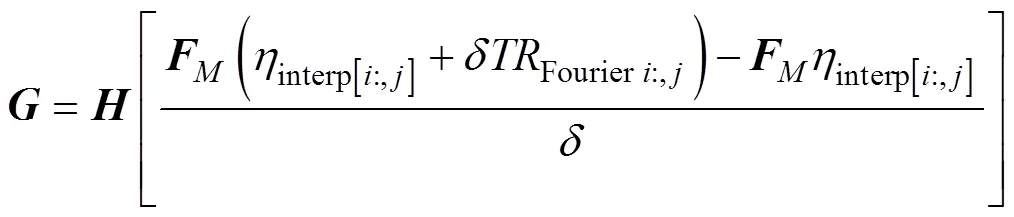
whereis the covariance matrix;is the linear response of the propagator of the frequency domain;is the dynamic propagator;0is the original SSH observation data, obtained from the parallelized along-track sampling simulation;interp[i:,j]is the interpolation SSH matrix of time domain, whose initial matrix is calculated through the multi-core parallelization, from Eqs. (6) to (9);interpis the Fourier transform matrix of the interpolation SSH value with target wavelengths;Fourier i:,jrepresents the process of Fourier transform,andare the coordinates of the searching space (the range oforis from 1 to,Î);Cis the covariance of the interpolating target location (the same as the time domain mentioned above); andis the covariance matrix of measurement error between all pairs of observations.

3.3 Data Mosaic

After the DI of each subregion obtained is calculated through data segmentation, data mosaic was performed on the DI results for each corresponding subregion, so that a complete one-cycle DI data mapping result could be obtained.

Fig.4 is an illustration of the data mosaic. Subregion 1, subregion 2, and their region expansions (REs) are includ- ed in the figure. Appropriate REs should be performed in the subregion division. For example, 5 positions or 10 positions should be enlarged from top to bottom; this will ensure that there are fewer fracture phenomena to facilitate the subsequent subregion data mosaic.

Each subregion is divided into two areas or patches: one is the major part of the subregions (., subregion 1, subregion 2, Fig.4); the other is the region expansion overlap of two adjacent subregions (., RE1, RE2, RE3, RE4, Fig.4). The region expansion areas or patches will be introduced in the data mosaic method to avoid missing mesoscale or sub-mesoscale phenomena in the boundary of the subregions of the data segmentation. If the weight of the RE SSH (includingand) is in the range of the along-track true values, for instance, 1.00≥SSH weight≥0.75, the DI SSH at the REs will be maintained. Otherwise, the PA-DI result value would be ignored.

This method accelerated the DI calculation processes of PA-DI in each cycle and finally could more efficiently obtain the global gridding data (see Section 4 for more information).

4 Mapping Experiments and Discussion

First, a high-resolution PA-DI test (described in Section 4.1) was implemented using the Oregon-region data in a one-cycle period to evaluate the algorithm applicability. The second mapping experiment (Section 4.2) was imple- mented with the parameters of the Guanlan satellite (Orbit 2 of 791.254km altitude, as described in Section 3) and was mainly utilized to evaluate the data segmentation and data mosaic algorithms. Lastly, the third experiment (Section 4.3) showed the ability of global SSH mapping with the PA-DI method.

4.1 PA-DI Applicability Tests: Oregon-Region Data Mapping Experiments

An along-track PA-DI result for Orbit 2 of the Guanlan satellite at the Oregon-region (124˚–130˚W, 42˚–48˚N) location in a one-cycle period is illustrated in Fig.5. The number of cross-traces is 23, 38, 66, 105, …, 407,., of the Guanlan high orbit. The test data are from OREGON-0100 to OREGON-0113 netCDF files of the SWOT simulator model data.

Fig.4 Illustration of region expansions and their subregions: (a), sketch of the method; (b), experimental schematic (the north tropical region in WPO).

Fig.5 Illustration of along-track PA-DI in Oregon-region, @ 2km×2km resolution.

Fig.5 illustrates the non-smooth situations of along-track PA-DI on WSAS (the details are shown from the PA-DI processing). During the along-track PA-DI experiment pro-cess, data segmentation and data mosaic were implemented to improve the mapping performance.

Table 2 illustrates the root mean square error (RMSE) of the Oregon-region PA-DI performance without or with mosaic, compared with the 1-track original along-track sampled data. Theof the PA-DI performance with mosaic was less than that of the performance without mo- saic.

Thecan be defined as follows:

wherehis the interpolation estimates of each calculation step of PA-DI or single-threaded DI, andtruerepresents the truth; the locations oftrueandhexist for 1, 2, …,, andis from 1 to,Î.

The results of data mapping and the applicability of the PA-DI algorithm, for 4.5˚×5.5˚ Oregon-region, are verified.

Fig.6 shows each intermediate process of the calculation steps, based on the SWOT simulator dataset of the Oregon-region (Fu and Ferrari, 2008; Durand., 2010; Gaultier., 2016). Figs.6a–e include the original data mapping results (Figs.6a–c), OI results (Fig.6d), and PA- DI results (Fig.6e). Fig.6e restores and expresses the oceanphenomenon from the original data (shown in Fig.6c). Figs.6f and g are the differences between theOI results and the true data and between the PA-DI results and the true data (Fig.6c), respectively, which illustrates that the difference between the PA-DI result and the day4 true data was much smaller than that between the OI result and the true data.

Table 2 RMSE of PA-DI performance with or without mosaic (@2km×2km resolution)

Fig.6 (a), OREGON-0106 grid data in SWOT simulator dataset of the 4.5˚×5.5˚ Oregon-region, as day t0 true data; (b), OREGON-0110 grid data from the dataset of the 4.5˚×5.5˚ Oregon-region, as day t8 true data; (c), OREGON-0108 grid data in the dataset of the 4.5˚×5.5˚ Oregon-region, as day t4 true data; (d), OI result of day t4; (e), PA-DI result of day t4 based on day t0 and day t8 PA-DI; (f), difference between (d) and (c); (g), difference between (e) and (c) (@2km×2km resolution).

The geostrophic velocity was derived from the true SSH, PA-DI result, and OI result, as shown in Fig.7a, Fig.7b, and Fig.7c, respectively.

The derivation formula of the geostrophic velocities is as follows:

whereuandvare the velocities,is the gravity constant, andis the Coriolis parameter.

To test the enhancement of the PA-DI applicability in mapping, the PA-DI and single-threaded DI (DI, no parallel) experiments were both conducted for the Oregon- region.

Table 3 compares thes among the algorithms (OI, DI (No Parallel), and PA-DI). Thes of the DI (no parallel) and the PA-DI algorithms were smaller than that of the OI method, which shows that the PA-DI algorithm is feasible for obtaining the necessary data mapping effect in principle, theoretically.

The DI (no parallel) and the PA-DI errors changed to lesser extents than OI errors (Table 3), and theof the PA-DI was smaller, which means that both the DI (no parallel) and the PA-DI algorithm could improve the map- ping accuracy better than the OI method. After forward or backward time-domain calculations in different time domains, the target center days were designed to be evaluated by OREGON-0104, OREGON-0106, and OREGON- 0108 original data, and thes of the PA-DI were at the same level as the DI (no parallel).

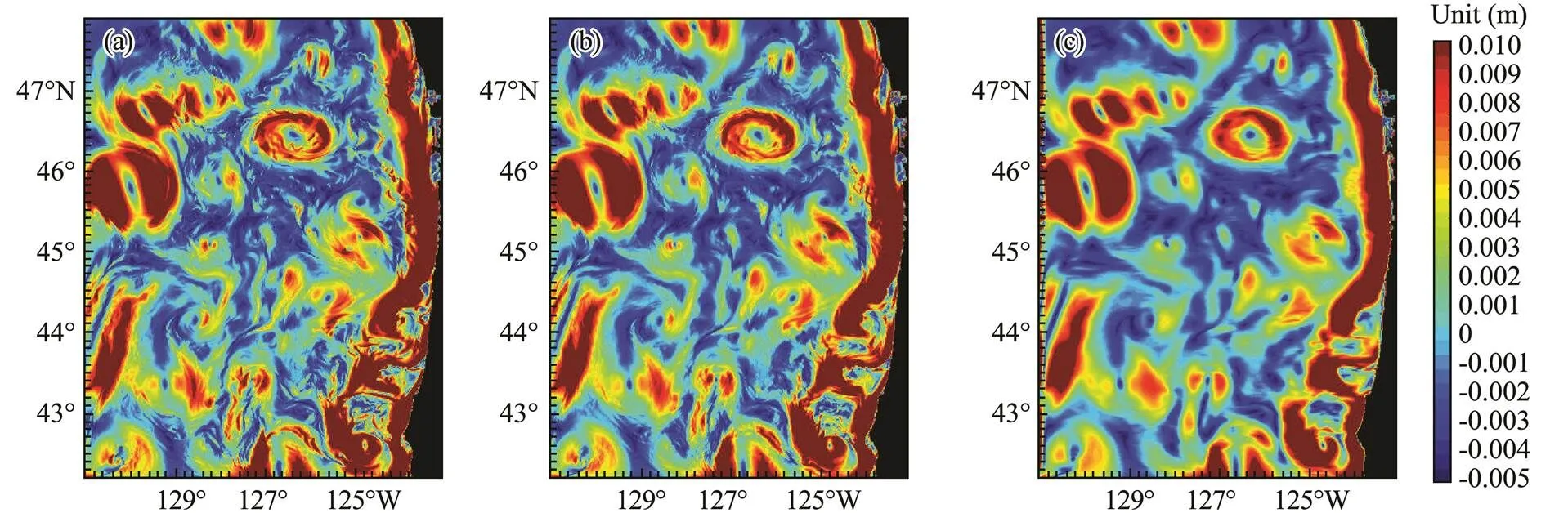
Fig.7 (a), Absolute geostrophic velocity derived from Fig.6c (the true data); (b), absolute geostrophic velocity derived from Fig.6e (DI result); (c), absolute geostrophic velocity derived from Fig.6d (OI result).

Table 3 RMSE values of Oregon-region PA-DI

In the global ranges of 80˚S–80˚N and 0˚–360˚, according to the spatial resolution of mapping, the data vo- lume will be 1.5TB@ 2km×2km resolution and 5TB@1km×1km resolution (21-day cycle for SWOT or 14-day cycle for Guanlan). However, for the same dataset, when the single-threaded DI (DI, no parallel) was used for only one- day mapping of the Oregon-region (the day of the corresponding OREGON-0108 file in the SWOT simulator data- set), the generation time reached 240h. Therefore, it is as- sumed that if the data sampled from the WSAS were map- ped in the global ranges, the operation time of the DI algorithm running on a single-threaded method will be unpredictable. The PA-DI algorithm will more efficiently ob- tain the data mapping result corresponding to the grid file of the target day.

The parallel speedup is 113 times and is calculated as follows:

The details of the efficiency improvement are as follows: the data mapping results of PA-DI in the Oregon- region can restore the oceanic phenomena of the regional model data, and in the case of a long timespan, PA-DI can also better express the oceanic physical phenomena in the region, especially the smaller sub-mesoscale phenomena. The speed increase details are shown in Table 4.

Table 4 illustrates the case of computations without parallelization, the processing time of which was about 35500s, but for the computation implemented through the PA-DI algorithm, the speed was significantly accelerated.

Table 4 Parallel computing process experiment results(@2km×2km resolution)

4.2 PA-DI Simulating Experiments on HYCOM Data on the West Pacific Ocean

Before each along-track data is segmented, the effect of subregion data mosaic should be considered, and observation coordinate-repetitions should be calculated out in advance. Since the Coriolis parameter values are positively related to latitudes, there must be a correction of projection before the data mosaic process.

Fig.8 shows an example of data mosaic after region partition into subregions. The Coriolis parameter values that were used to calculateandduring the whole pro- cess of PA-DI were changed following the latitude @ 1/12˚×1/12˚ resolution (Fig.8a), which means that a projection- correction was needed before the data mosaic implementation (Fig.8b), for instance, the correction of universal transverse Mercator projection. Moreover, a data mosaic result of the subregion is shown in Fig.8c.

Taking April 23, 2015, as the target date, and using the along-track sampling simulation of HYCOM data from April 17, 2015, to April 30, 2015, the OI method and PA- DI method were used to reconstruct the mapping data. The results and comparisons are shown in Fig.9.

Fig.9a shows the true value of HYCOM data as the ori- ginal data for result comparison. Fig.9b is the result of OI using the along-track sampling simulation of HYCOM data from April 17, 2015, to April 30, 2015. Fig.9c is the result of PA-DI for April 23, 2015, as the target date, and Figs.9d and e show the differences between OI and the original data and PA-DI and the original data, respectively. From Fig.9, the PA-DI method is superior to the OI me- thod for the WPO region, and it can preliminarily restore the ocean phenomena smaller than mesoscales.

Thewas used to evaluate the performance of the WSAS mapping, and the PA-DI implementation was used to output the mapping experiment results of the WPO re- gion. Theof the results are summarized in Table 5. Table 5 presents the PA-DI RMSEs on WSAS simulation on HYCOM data. Although the resolution of HYCOM was 1/12˚, the sub-mesoscale can be well illustrated by this model. Table 5 summarizes thecorresponding to the above experiments. The error of PA-DI was generally far less than that of OI, and PA-DI could restore the sub- mesoscale ocean phenomena. The totalof global PA-DI will be a bit larger than that for each subregion, but thes will be in the same acceptable ranges.

Fig.8 Subregion in the latitude range of 17˚–21˚N and longitude range of 160˚–170˚E location (following 1/12˚×1/12˚ resolution on latitude directions from south to north): (a), region partition of along-track sampled SSH by Coriolis parameter, which was changed following the latitude directions; (b), data mosaic by the correction from a method of universal transverse Mercator projection; (c), result of subregion data mosaic.

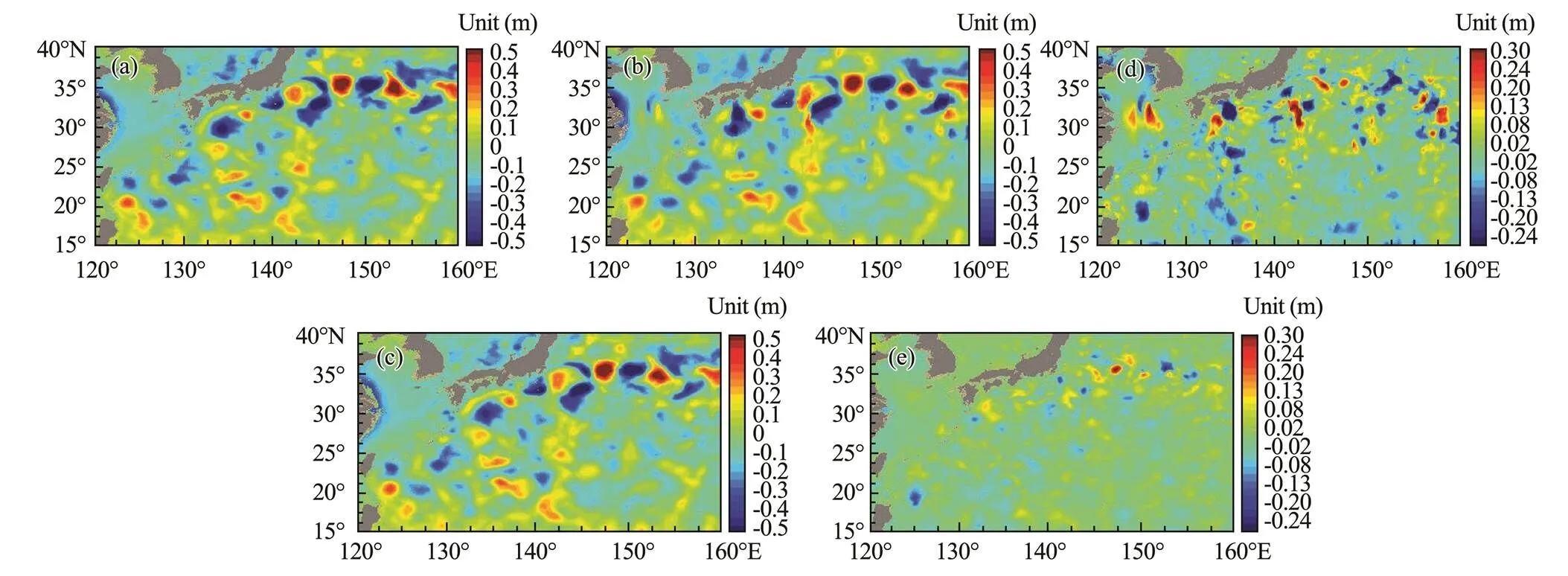
Fig.9 (a), The true value of HYCOM data as the original data for result comparison; (b), the result of OI using the along-track sampling simulation of HYCOM data from April 17, 2015, to April 30, 2015; (c), the result of PA-DI for April 23, 2015, as the target date; (d), the differences between OI and the HYCOM true data; (e), the differences between PA-DI and the HYCOM true data.

Table 5 PA-DI RMSE on WSAS in the WPO region

4.3 PA-DI Experiments on Global HYCOM Data

Experiments were conducted with the parameters of the Guanlan satellite (the 791.254km orbit altitude), in which the WSAS along-track PA-DI on 2015 global HYCOM SSH data was applied. The data in one year were chosen to implement the along-track data sampling simulation with Orbit 2 parameters of the Guanlan satellite, and the global sampled data were stored step by step in each cycle per day; then, the spatial-temporal parallel-DI was accom- plished. An example of the PA-DI mapping results on the glo-bal HYCOM dataset is shown in Fig.10 (for data of July 11, 2015).

The grid mapping data of the corresponding satellite along-track sampled SSH in each day were calculated using the PA-DI algorithm. A random normal day’s HYCOM data from each season were chosen to validate the PA-DI performance. The results are shown in Fig.11.

The global grid data mapping results for four random normal days are shown in Fig.11. Figs.11a, c, e, and g show the global PA-DI data mapping performances of HYCOM on January 20, April 20, August 20, and December 20, 2015, respectively. Figs.11b, d, f, and h show the HYCOM true values of corresponding dates. The global mapping data of January 20, April 20, August 20, and December 20, 2015, were selected because these four dates represent the typical climatic characteristics of the corresponding seasons. In the northwestern Pacific Ocean, the Kuroshio, and the Gulf Stream, the mesoscale and the sub-mesoscale ocean phenomena are stronger in summer and autumn and are weaker in spring. In the Atlantic Ocean, the phenomena ex- tend to the north during winter. In the southern hemis- sphere subtropics, the mesoscale and the sub-mesoscale ocean phenomena are also stronger during austral summer and weaker in winter. Using these dates makes it convenient to identify, evaluate, and judge the ability of the PA- DI algorithm to restore and describe ocean phenomena.These preliminary results are based on one year of data only, and the results should be confirmed over a longer period.

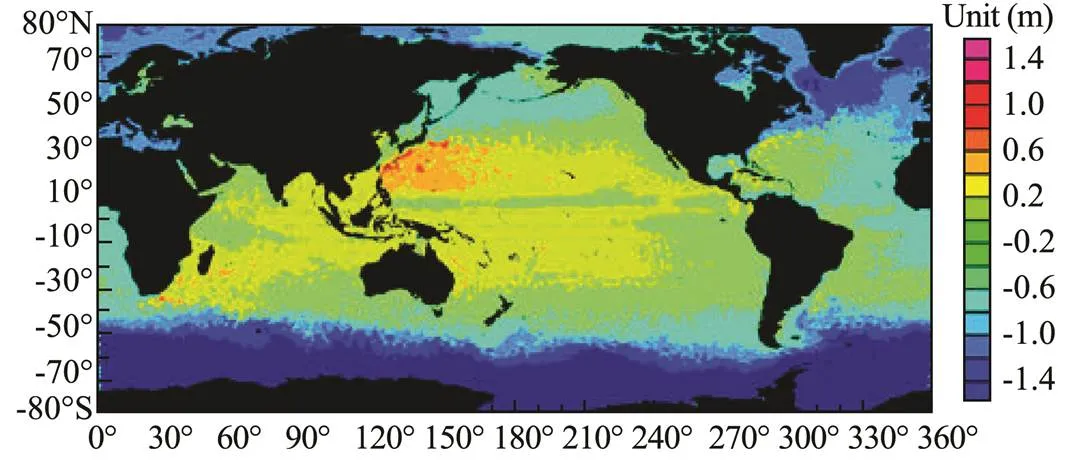
Fig.10 Example of PA-DI operation results on the global HYCOM dataset (July 11, 2015).

Fig.11 PA-DI global data mapping effect of January 20, April 20, August 20, and December 20, 2015 (a, c, e, and g), was compared with the true values of HYCOM (b, d, f, and h) for the corresponding dates.

Figs.12a, c, e, and g show the global PA-DI data mapping performances of HYCOM on January 20, April 20, August 20, and December 20, 2015, respectively. Figs.12b, d, f, and h show the difference between Figs.12a, c, e, and g diagrams and the HYCOM true values for the corresponding dates. It can be seen that on the global scale, the PA-DI method could map the data acquired by the WSAS simulation, which had fewer differences between the HY- COM SSH true values. The PA-DI method could well re- store the ocean phenomena of the original data, which successfully reconstructed the SSH field in the full space and time domains considered.

Fig.12 PA-DI global data mapping effect of (a) January 20, 2015; (c) April 20, 2015; (e) August 20, 2015; and (g) December20, 2015. (b), (d), (f), (g), the difference between (a), (c), (e), and (g) and the HYCOM true values for the corresponding dates.

With the acceleration of the PA-DI algorithm, the task was decomposed into K computer CPU cores for operation, and the region of global latitude range of 80˚S–80˚N and longitude range of 0˚–360˚ were divided intosubregions following each along-track sampled data. There- fore, the PA-DI algorithm ran parallel withsubregions usingcomputer CPU cores (each CPU had 10 threads). The time complexity was optimized and reduced from O(3) to O(3/), and the operation efficiency was in- creased, meeting the accuracy and efficiency requirements of satellite data mapping and achieving the desired results. The efficiency of the parallel-DI algorithm during the pro- cesses is presented in Table 6.

As shown in Table 6, when=10, and=4 to 12, the one-year global HYCOM PA-DI calculation process will continue for at least 22d, but when=160, then the calculation time could be reduced to 1 day. Table 7 shows theof PA-DI on the global HYCOM model.

Table 6 Efficiency of one-year HYCOM global parallel-DI processes’ test results

Table 7 PA-DI RMSE on global HYCOM dataset

The computer configuration used in this paper is described in Table 8.

Table 8 Computer hardware resource in this paper

5 Conclusions

The PA-DI algorithm proposed in this paper utilizes the data processing and analysis techniques of data science, combined with satellite remote sensing and physical ocea- nography theory and methods. This multi-inter-disciplinary approach was applied to SSH data mapping, and the DI method was successfully parallelized and accelerated, which provided an effective method with high performance and precision for the future WSAS sampled data mapping, and improved the mapping efficiency of the WSAS.

In this study, based on the Guanlan orbit parameters,the PA-DI algorithm was tested on the Oregon-region dataof the SWOT simulator, the WPO HYCOM region data, and the global HYCOM data. The experiment processes, which include the along-track sampling simulation on OSSEs, data segmentation, parallel-DI calculation, and data mosaic, were implemented, and the experiment results were obtained, and the data were analyzed. The algorithm was found to improve the mapping efficiency for the WSAS.

According to the experiment results, the PA-DI algorithm can significantly improve the operational efficiency, and the algorithm has the potential to achieve mapping for currently archived data. After parallel processing, the current time-domain data mapping based on time data could provide efficient and reliable data sources for the analysis of frequency-domain data converted from the time-domain to frequency-domain. The PA-DI method could provide high-resolution and low-error products for WSAS with high efficiency without compromising accuracy. The results show that the grid mapping method with the PA-DI algorithm has strong data reconstructing ability, which meets the data quality requirements of WSAS.

In the future, we will improve the mapping method, to obtain more accurate and reliable data mapping products for WSAS and marine science. Moreover, we will also consider introducing artificial intelligence methods (machine learning (Lguensat., 2019), especially deep lear- ning) into the PA-DI process, which is a future research direction.

Acknowledgements

This research was funded by the Key Research and De- velopment Program of Shandong Province (No. 2019GH Z023), the National Natural Science Foundation of China (Nos. 41906155, 42030406), the Fundamental Research Funds for the Central Universities (No. 201762005), and the National Key Scientific Instrument and Equipment De- velopment Projects of National Natural Science Foundation of China (No. 41527901).

Amores, A., Jordà, G., Arsouze, T., and Sommer, J., 2018. Up to what extent can we characterize ocean eddies using present- day gridded altimetric products?, 123:7220-7236.

AVISO (Archiving, Verification and Interpretation of data ofSatellites Oceanography), 2019. Available online: https://www.aviso.altimetry.fr/en/home.html (accessed on 2 January 2021).

Bretherton, F. P., Davis, R. E., and Fandry, C. B., 1976. A technique for objective analysis and design of oceanographic experiments applied to MODE-73., 23: 559- 582.

Chavanne, C. P., and Klein, P., 2010. Can oceanic submesoscale processes be observed with satellite altimetry?, 37: L22602.

Chelton, D. B., Deszoeke, R. A., Schlax, M. G., Naggar, K. E., and Siwertz, N., 1998. Geographical variability of the first baroclinic rossby radius of deformation., 28: 433-460.

Chen, G., Tang, J., Zhao, C., Wu, S., Yu, F., Ma, C.,., 2019. Concept design of the ‘GuanLan’ science mission: China’s novel contribution to space oceanography (Ocean OBS19’)., 6: 1-14.

CNES, 2016. SSALTO/DUACS user handbook: MSLA and (M) ADT near-real time and delayed time products.CLS-DOS- NT-06-034.AVISO, 5-35.

Cormen, T. H., Leiserson, C. E., and Rivest, R., 2009.,3rd edition. MIT Press, Massachusetts, 120- 310.

Durand, M., Fu, L. L., Lettenmaier, D. P., Alsdorf, D. E., Ro- driguez, E., and Fernandez, D. E., 2010. The surface water and ocean topography mission: Observing terrestrial surface water and oceanic submesoscale eddies., 98: 766-779.

Dussurget, R., Birol, F., Morrow, R., and Mey, P. D., 2011. Fine resolution altimetry data for a regional application in the Bay of Biscay., 34: 447-476.

Forget, G., Campin, J. M., Heimbach, P., Hill, C. N., Ponte, R. M.,and Wunsch, C., 2015. ECCO version 4: An integrated framework for non-linear inverse modeling and global ocean state estimation., 8: 3653-3743.

Fu, L. L., and Ferrari, R., 2008. Observing oceanic submesoscaleprocesses from space., 89: 488-488.

Fu, L. L., and Flierl, G. R., 1980. Nonlinear energy and enstrophy transfers in a realistically stratified ocean., 4: 219-246.

Fu, L. L., and Rodriguez, R., 2004. High-resolution measurement of ocean surface topography by radar interferometry for oceanographic and geophysical applications., 19: 209-224.

Fukumori, I., 2002. A partitioned Kalman filter and smoother., 130: 1370-1383.

Gaultier, L., Ubelmann, C., and Fu, L. L., 2016. The challenge of using future SWOT data for oceanic field reconstruction., 33: 119-126.

Gaultier, L., Ubelmann, C., and Fu, L. L., 2017. SWOT simulator documentation, NASA (accessed 15 Mar 2017, Release 2. 3.0), 1-21. Available online: http://swot.jpl.nasa.gov/science/ resources/ (accessed on 2 January 2021).

Halliwell, G., and Wallcraft, A., 2018. Naval research laboratory: Ocean dynamics and prediction branch, Hybrid Coordinate Ocean Model (HYCOM): 01 January 2015–31 December 2018. Available online: ftp://ftp.hycom.org/datasets/GLBu0.08/exp t_91.1/ hindcasts/2015/ (accessed on 2 January 2021).

KerrAaron, P. C., Donahue, S., Westerink, J. J., and Cox, A. T., 2013. U.S. IOOS coastal and ocean modeling testbed: Inter-model evaluation of tides, waves, and hurricane surge in the Gulf of Mexico.,118: 5129-5172.

Lapeyre, G., and Klein, P., 2008. Dynamics of the upper oceanic layers in terms of surface quasigeostrophy theory., 36: 165-176.

Le Traon, P. Y., Faugère, Y., Hernandez, F., Dorandeu, J., Mertz, F., and Ablain, M., 2003. Can we merge Geostat follow-on with TOPEX/Poseidon and ERS-2 for an improved description of the ocean circulation?, 20: 889-895.

Le Traon, P. Y., Nadal, F., and Ducet, N., 1998. An improved mapping method of multisatellite altimeter data., 15: 522-534.

Lguensat, R., Viet, P. H., Sun, M., Chen, G., Fenglin, T., Chapron, B.,., 2019. Data-driven interpolation of sea level anomalies using analog data assimilation., 11: 858.

Liu, Y., Chen, G., Sun, M., Liu, S., and Tian, F., 2016. A parallel SLA-based algorithm for global mesoscale eddy identification., 33: 2743-2754.

Ma, C., Guo, X., Zhang., H., Di, J., and Chen, G., 2020. An in- vestigation of the influences of SWOT sampling and errors on ocean eddy observation., 12: 2682-2698.

Martin, S., 2014..2nd edition. Cambridge University Press, New York, 88-210.

Mather, R. S., Rizos, C., and Coleman, R., 1979. Remote sensing of surface ocean circulation with satellite altimetry.,26: 11-17.

Melab, N., Gmys, J., Mezmaz, M., and Tuyttens, D., 2018. Multi- coremany-core computing for many-task branch-and- bound applied to big optimization problems., 82: 472-481.

Mohamed, M. A., Abouelsoud, M. E. A., and Eid, M. M., 2004. A comprehensive ocean prediction and analysis system based on the tangent linear and adjoint of a regional ocean model., 7: 227-258.

Morrow, R., and Le Traon, P. Y., 2012. Recent advances in ob- serving mesoscale ocean dynamics with satellite altimetry., 50: 1062-1076.

Morrow, R., Fu, L. L., Ardhuin, F., Benkiran, M., Chapron, B., Cosme, E.,., 2019. Global observations of fine-scale ocean surface topography with the surface water and ocean topography (SWOT) mission (Ocean OBS19’)., 6: 1-19.

Peral, E., and Esteban-Fernandez, D., 2018. SWOT mission per- formance and error budget.–. Valencia, 8625-8628.

Pie, N., and Schutz, B. E., 2008. Subcycle analysis for icesat’s repeat groundtrack orbits and application to phasing maneuvers., 56: 325-340.

Pedlosky, J., and Leibovich, S., 1987.. Springer-Verlag, New York, 230-360.

Roosta, S. H., 2000.. 2nd edition. Springer-Verlag, New York, 20-75.

Tang, W., Feng, W., Deng, J., Jia, M., and Zuo, H., 2018. Pa-rallel computing for geocomputational modeling. In:. Thill, J. C., and Dragicevic, S., eds., Springer, Cham, 37-54.

Ubelmann, C., Cornuelle, B., and Fu, L. L., 2016. Dynamic mapping of along-track ocean altimetry: Method and perfor- mance from observing system simulation experiments., 33: 1691-1699.

Ubelmann, C., Fu, L. L., Brown, S., Peral, E., and Esteban-Fer- nandez, D., 2014. The Effect of atmospheric water vapor con- tent on the performance of future wide-swath ocean altimetry measurement., 31: 1446-1454.

Ubelmann, C., Klein, P., and Fu, L. L., 2015. Dynamic interpolation of sea surface height and potential applications for future high-resolution altimetry mapping., 32: 177-184.

Vidard, A., Bouttier, P. A., and Vigilant, F., 2015. NEMOTAM: Tangent and adjoint models for the ocean modelling platform NEMO., 8: 1245-1257.

Wunsch, C., 1996.Cambridge University Press, Cambridge, 66-110.

Zhen, Y., Tandeo, P., Leroux, S., Metref, S., and Sommer, J. L., 2020. An adaptive optimal interpolation based on analog fore- casting: Application to SSH in the Gulf of Mexico., 37 (9): 1697-1711.

. Tel: 0086-532-66781812 E-mail: chunyongma@ouc.edu.cn

July 10, 2020;

October 21, 2020;

November 4, 2020

© Ocean University of China, Science Press and Springer-Verlag GmbH Germany 2021

(Edited by Chen Wenwen)