相干信源条件下的稀疏贝叶斯DOA估计*

何文超，梁龙凯，弓 馨

(长春人文学院 理工学院，长春130117)

0 引 言

波达方向(Direction of Arrival,DOA)估计是阵列信号处理领域的重要研究方向之一。山峰、海平面等障碍物对信源进行反射所造成的多径干扰，均会使得传感器阵列接收到的回波信号是相干的。因此，研究相干信源的DOA估计尤为重要。现阶段主要的方法是采用子空间平滑(Subspace Smoothing，SS)技术对协方差矩阵进行处理，并对处理后的矩阵采用子空间类算法，如MUSIC等[1-2]。但是，基于子空间类的算法在小快拍、低信噪比下信号估计性能显著退化[3-4]。压缩感知理论的提出[5-6]，使得在小快拍、低信噪比情况下能够获得较好的DOA估计性能。因此，可结合子空间平滑理论和稀疏恢复理论进行DOA估计。

早期的稀疏恢复算法采用的是全局匹配滤波器(Generalized Matched Filter,GMF)[5]，其中，性能较好的算法是l1-SVD[6]。文献[7-8]指出，l1-SVD问题可以看成是子空间加权拟合(Weighted Subspace Fitting,WSF)的过程。文献[9]给出了一种加权子空间拟合问题的稀疏表示，并指出此类问题的约束条件应是l0-norm，而实际上往往采用l1-norm代替。针对文献[9]给出的稀疏信号模型，可以通过基于凸优化的lp范数法[10]以及基于贪婪思想进行迭代重构的MP算法[11-15]。此类方法的解可能收敛于局部极值点，无法保证全局最优解，当信源间具有较强相关性时性能下降[16]。稀疏贝叶斯类算法被认为是唯一一种与l0范数优化具有相同全局收敛性的稀疏重构方法。文献[17]提出了一种离格贝叶斯算法(Off-grid Sparse Bayesian Interference，OGSBI)，在降低计算量的同时能够提高DOA估计精度。

本文针对现有的稀疏贝叶斯算法无法解决相干信源的DOA估计问题，将子空间平滑技术与稀疏恢复理论相结合，提出了SS-OGSBI算法。考虑到在小快拍下、有限长采样条件下的信号子空间与实际的信号子空间无法完全重合，结合子空间拟合技术，在最小二乘意义使得有限长采样条件下的信号子空间与实际的信号子空间重合，提出了一种基于子空间拟合与子空间平滑技术的信号模型，并与离格稀疏贝叶斯算法相结合，进一步提出了SS-WSF-OGSBI算法。与经典的基于贝叶斯恢复的DOA估计算法进行对比试验，证明了所提本算法的有效性。

1 信号模型

本文所研究的是在高斯噪声背景下均匀线性阵列模型DOA参数估计，对于所有的回波信号均为远场窄带相干信号。接收信号可以表示为

Y(t)=AX(t)+N(t)，t=1,2,…,T。

(1)

式中：Y为信号接收阵列，M×T维矩阵，M是阵元数；T是快拍数；A是阵列流形，

A=[a(θ1)a(θ2) …a(θk)]，

接收阵列的协方差矩阵可以表示为

(2)

对式(2)做子空间平滑处理，得到

(3)

式中：ES和EN分别式信号子空间和噪声子空间所对应的特征向量;Λ和Γ是信号子空间和噪声子空间对应的特征值；L是子空间阵列数；Rl是子空间协方差矩阵，

Rl=R(l:l+M-1,l:l+M-1) 。

(4)

式中：M是子空间协方差矩阵的维数。

在有限采样数据情况下，阵列流形张成的子空间与实际的信号子空间不能完全重合，而WSF算法在最小二乘意义下可以使得拟合的效果最好。

由文献[9]可知，式(3)可以转化成WSF问题，如下：

(5)

(6)

(7)

式中：N是估计误差。由文献[9]知，模型(5)的估计误差是卡方分布，即近似高斯分布，因此，模型(7)的误差也为近似高斯分布，所以其噪声概率密度函数可以由高斯函数近似表示。这与稀疏贝叶斯模型相一致，因此可以通过文献[17]提出的OGSBI算法进行参数估计。

2 OGSBI算法

式(7)的信号模型与稀疏贝叶斯模型一致，此时可用OGSBI算法恢复目标DOA。OGSBI算法可看成是传统的SBL(Sparse Bayesian Learning)算法与离格算法的组合。

2.1 SBL算法

对于式(7)的信号模型，可以看成如下形式：

Y(∶,i)=φ(θ)X(∶,i)+N(∶,i),i=1,2,…,T。

(8)

假设X的每一列向量均是相互独立且符合高斯分布的随机变量，那么其似然函数可以表示为

(9)

对于参数δi，通常假设其符合Gamma分布，如下：

(10)

式中：参数ρ通常取为很小的正数，此处取ρ=0.01。

信号Y的似然函数为

(11)

根据贝叶斯原理，由公式(9)、(11)可知，

(12)

式中：

(13)

(14)

根据SBL算法原理，需要更新超参数α0和δ(注Δt=diag(δ))。此处按照文献[17]的方法，直接给出：

(15)

(16)

式中：Ξt≅μt(μt)H+Σt。

2.2 离格(OG)算法

稀疏贝叶斯算法是假设目标DOA在搜索字典中，当目标位置在相邻两个网格之间时，会产生较大误差。离格贝叶斯算法是在此基础上提出的，其思想是在相邻两个网格点之间做一阶泰勒展开式得到的。

(17)

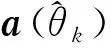
根据文献[17]，直接给出β更新方法为

(18)

式中：

(19)

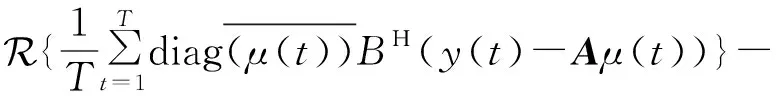
(20)

3 本文提出的算法

3.1 SS-OGSBI算法

针对OGSBI算法无法解决相干信源DOA估计问题，本文将子空间平滑技术(SS)与OGSBI算法相结合，提出了SS-OGSBI算法。下面介绍算法原理。

根据信号模型(1)，获得接收信号的协方差矩阵(2)，结合子空间平滑技术可获得式(3),式(3)可变换为

(21)

对式(21)做特征值分解，可得到

(22)

式中:Σ是对角矩阵。结合式(21)、(22)及式(1)可知，

U=A′X′+N′ 。

(23)

式中：A′是导向矢量矩阵，维度是M×NS，M是子空间矩阵的维度，NS是目标数;X′是变换矩阵;N′是估计误差。矩阵U和ES均可以通过导向矢量A′的线性变换得到。

式(23)的信号模型与OGSBI算法的信号模型一致，即可应用OGSBI算法估计式(23)中的X′，所估计的目标DOA即在X′的非零行上。

算法的Matlab伪代码如下：

3 根据式(21)～(23)可获得信号模型U=AX′+N′。

6 由式(14)和式(13)计算Σt和μt。

7 由式(15)和式(16)计算α0和δi。

8 由式(18)～(20)更新参数β。

9 由式(17)更新导向矢量φ(θ)。

10 判断当条件‖δ(l)-δ(l-1)‖2/‖δ(l-1)‖2<ε时(仿真中，ε=0.001)，继续执行下一步，否则跳转步骤6。

3.2 SS-WSF-OGSBI算法

3.1节所提出的SS-OGSBI算法在小快拍、低信噪比情况下，式(21)中的信号子空间ES与无限长采样下的信号子空间有很大的估计误差，使得模型(23)的估计误差显著增大。因此，我们提出采用子空间加权拟合算法，使得有限长采样下的信号子空间与实际的信号子空间在最小二乘意义下接近。

算法的Matlab伪代码如下：

6 由式(14)和式(13)计算Σt和μt。

7 由式(15)和式(16)计算α0和δi。

8 由式(18)～(20)更新参数β。

9 由式(17)更新导向矢量φ(θ)。

10 判断当条件‖δ(1)-δ(l-1)‖2/‖δ(l-1)‖2<ε时(仿真中，ε=0.001)，继续执行下一步，否则跳转步骤6。

3.3 信号功率谱

(24)

对式(21)进行谱峰搜索(findpeaks函数)，峰值位置所对应的θfinal角度即是估计的DOA角度。

4 仿真实验

仿真实验中，信号采用两个频率、相位完全相同的BPSK信号，从不同的方向角度入射天线阵列。定义信噪比为

(25)

4.1 一次估计性能

实验条件：网格间距2°，信噪比10 dB，采样点数20，阵元数10，取阵元间距为信号波长的1/2。目标角度随机选取，两个目标角度的范围分别为[60°,62°]和[120°,122°]。归一化的谱估计结果如图1所示。

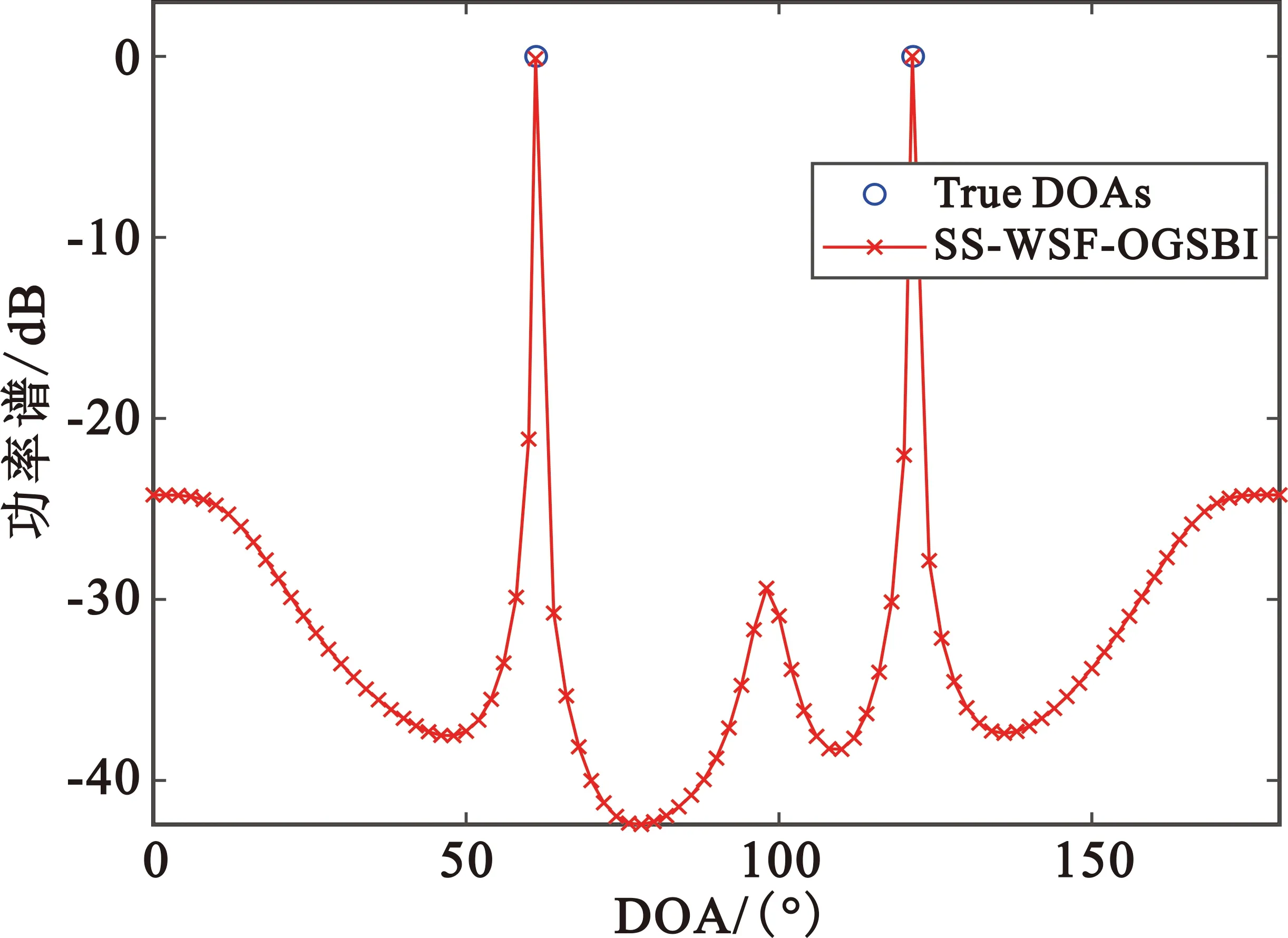
图1 SS-WSF-OGSBI一次估计性能

4.2 信噪比

图2 SS-OGSBI一次估计性能

图3 均方根误差随信噪比变化

由图3可知，文献[14]算法为非离格类算法，当目标DOA在网格点之间时，即使在高信噪比条件下仍有较大的估计误差，算法失效。文献[17]的OGSBI算法能够解决离格问题，但对于相干信源，在低信噪比下有较大的估计误差。SS-OGSBI能够处理相干信源和离格DOA估计问题，但在小快拍、低信噪比下，由于有限采样条件下的信号子空间与实际的信号子空间有较大的估计误差，与SS-SWF-OGSBI算法相比性能略差。SS-SWF-OGSBI算法与SS-OGSBI算法，在-4 dB下误差相差0.2°左右，在10 dB下误差相差0.015°左右。

4.3 成功率

图4 成功率实验

由图4可知，在采样点为20时，文献[14]与文献[17]算法成功率明显小于其他两种算法。这主要因为当目标位置在网格点以外时，这两种算法失效；尤其在低信噪比情况下，在角度分辨率为2°时，成功率低于0.2。SS-OGSBI算法能够有效处理离格问题和相干信源问题，但在小快拍条件下，由于所估计的信号子空间偏离实际的信号子空间，使得算法性能低于SS-WSF-OGSBI算法。信噪比在3 dB以上时，两种算法的角度估计误差均能保持在1°以内。

4.4 均方根误差随快拍数变化

实验条件：信噪比为-5 dB，快拍数变化范围是100～1 000，每次间隔100，其他条件与4.2节相同。做100次蒙特卡洛实验，实验结果如图5所示。

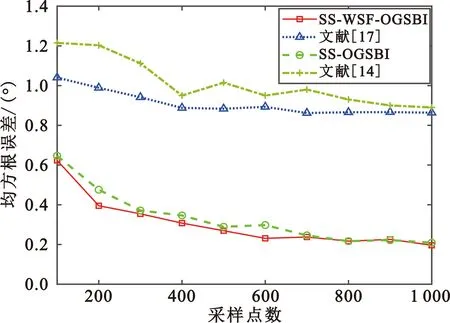
图5 均方根误差随快拍数变化

由图5可知，本文提出的两种算法性能在低信噪比下明显优于其他两种算法。本文所提的SS-WSF-OGSBI算法与SS-OGSBI算法相比，当快拍数小于600时，由于有限长采用下的信号子空间与实际的信号子空间偏差较大，使得SS-WSF-OGSBI算法性能优于SS-OGSBI算法。当快拍数大于700时，有限长采样下的信号子空间接近实际的信号子空间，使得两种算法的性能基本一致。文献[17]算法和文献[14]算法无法解决相干信源条件下的离格DOA估计问题，尤其在低信噪比(-5 dB)下，性能严重退化，估计误差均大于0.9°。

4.5 均方根误差随目标数变化实验

实验条件：网格间距2°，信噪比10 dB，采样点数20，阵元数10，取阵元间距为信号波长的1/2。目标角度随机选取，角度范围在[70°,72°]、[90°,92°]、[120°,122°]、[140°,142°]、[50°,52°]五个区间内。实验结果如图6所示。

图6 均方根误差随目标数变化

在实验中，均假设所有回波信号都是频率相同、相位相同的BPSK信号。由图6可知，随着目标数的增加，四种算法的均方根误差均会变大。当目标数为5时，文献[17]与文献[14]两种算法已经无法准确估计目标的方位角。在10 dB下，SS-WSF-OGSBI与SS-OGSBI相比，略优于后者。

在仿真过程中，阵元数取M=10,所能估计的最大目标数为5。当估计6个目标时，本文所提出的两种算法均无法准确估计目标。能够准确估计目标最大数目的证明如下：

当目标均为相干信号源时，为了保证损失的阵列孔径最小，在子空间平滑过程中，取子空间数L等于相干信号源数目K，而子空间矩阵是(M-L+1)维的方阵。能够准确估计目标的条件为(M-L+1)≻K,又因为L=K，可知

(26)

当所估计的目标数接近上述最大值时，算法的性能会显著下降，甚至无法准确估计目标DOA角度。

5 结束语

针对稀疏贝叶斯算法无法准确估计相干信源DOA问题，本文将子空间平滑技术与稀疏贝叶斯算法相结合，提出了SS-OGSBI算法。此算法能够有效解决相干信源和离格DOA估计问题，但在小快拍低信噪比条件下性能下降。针对此问题，提出了基于子空间平滑和子空间拟合的信号模型，并将此信号模型与稀疏贝叶斯算法相结合，提出了SS-WSF-OGSBI算法。此算法与SS-OGSBI算法相比，在小快拍低信噪比条件下性能有明显的改善。本文提出的信号模型亦可与其他稀疏恢复类算法相结合，来解决小快拍条件下的相干信源DOA估计问题。所提算法在不同信噪比下的算法估计性能、不同信噪比下的算法成功率均优于其他两种算法。

本文中所讨论的环境噪声均为高斯白噪声，在后续的研究中，可对高斯有色噪声以及α噪声环境下的相干信源DOA估计方法进行探讨。