四川盆地川西坳陷上三叠统须家河组储层各向异性地应力评价方法
张金才,范 鑫,黄志文,刘忠群,亓原昌
(1.中国石化 休斯顿研究开发中心,美国 休斯顿TX 77056;2.中国石化 石油勘探开发研究院,北京 100083)
四川盆地川西坳陷的致密砂岩气藏天然气资源量较丰富,截止到2017年底,中国石化在川西侏罗系与上三叠统保有天然气三级储量约为1.4×1012m3,主力气层是上三叠统须家河组和侏罗系蓬莱镇组、遂宁组与沙溪庙组,已发现并开发了中坝、平落坝、九龙山、合兴场、新场、洛带、新都、邛西和马蓬等气田[1-4]。其中中国石化的川西深层须家河组探明储量为1 773×108m3。然而,由于须家河组为致密砂岩,处于地质构造复杂并且构造应力很高的深层,因此储层难于压裂、压裂的加砂量很低,导致动用储量低,仅为227×108m3。为了提高储层的动用储量,迫切需要研究须家河组砂岩的地应力与岩石力学特征,为压裂改造的设计与施工提供科学依据。
须家河组含有5个层段,从浅部到深部包括须五段、须四段、须三段、须二段和须一段。其中须五段、须三段和须一段主要为泥岩(烃源岩)。须二段和须四段中的砂岩为主要储层,埋深为3 800~5 100 m。须二段沉积时期,研究区主要发育以辫状河三角洲为主的中-粗粒沉积体系,其中辫状河三角洲前缘水下分流河道和河口坝是研究区主要沉积微相类型。砂岩厚度大、平面分布广泛,但是储层非常致密(孔隙度为3%~5%,渗透率为0.07×10-3~0.10×10-3μm2),为地层压力异常超压的裂缝性砂岩气藏。先后有19口井投入试采,目前日产气约为49.9×104m3,日产水约655 m3。通过前期压裂认识和对比,须家河深层致密气压裂与其他地区非常不同,在裂缝起裂与扩展机理认识方面存在许多难点,对于不含天然裂缝的岩层常出现水力压裂压不开储层或施工泵压很高而导致压裂施工失败的情况,制约了深层须家河组气藏的开发。造成压裂效果不佳的主要原因是储层致密和高地应力。
须家河组深层致密砂岩储层处于印度板块和亚欧板块碰撞形成的高构造应力区,具有异常高的地应力,并且位于复杂构造下的走滑断层或逆断层应力区。在这种地应力条件下,压裂会产生低角度裂缝,导致水平井的储层改造效果不佳、垂直井的裂缝扩展高度低。另外,须家河组致密储层具有很高的岩石强度,与高地应力的组合造成更高的裂缝开启压力,进一步增加了储层改造的难度。例如新场须家河组储层的破裂压力梯度(24.8~31.9 MPa/km)远高于上覆岩层压力。另一个不利因素是压裂裂缝延伸压力梯度也很高(一般为24~26 MPa/km),从而抑制了裂缝的延伸范围。
以往的试验与研究表明,地应力控制着人工裂缝的起裂和扩展[5]。一般假设地应力由3个相互正交的主应力组成,即垂向应力(上覆岩层压力)、最大水平主应力与最小水平主应力。其中最小水平主应力决定着压裂裂缝的开启与扩展,而最大水平主应力主要决定着裂缝的扩展方向[6]。因此,对于复杂储层改造成功的前提是掌握地应力的特征与规律。研究人员已开展了须家河组储层地应力研究并得出了一些重要的成果[7-9]。最近进行的须二段砂岩大块露头岩样水力压裂试验表明,破裂压力主要取决于水平主应力与岩层的抗拉强度[10],最小水平主应力越高岩层的破裂压力越大、越难压裂。因此,正确评价水平主应力对压裂设计非常重要。另外,须家河的一些储层富含天然裂缝,须二段优质储层中高角度或垂直裂缝发育,导致了岩层的各向异性。对于这类储层如果采用常规的各向同性岩层的地应力评价方法,则会高估岩层的实际水平主应力。以往的研究未考虑裂隙储层对地应力的影响,因此需要获得这类储层的地应力评价方法。根据几十口井的实测数据与钻井资料,本文将分析须家河储层及其上覆岩层的地应力特征。此外,为了更好地评价优质储层的地应力及其对压裂的影响,本文将应用各向异性介质理论研究含天然裂缝储层水平主应力的预测公式与评价方法。
1 须家河组储层地应力实测结果
1.1 各向同性岩石地应力预测方法
对于各向同性岩石,最小与最大水平主应力可以用下面常用的预测公式[11-12]:
(1)
(2)
式中:σV,σH和σh分别是垂向应力、最大和最小水平主应力,MPa;pp是地层孔隙压力,MPa;α是比奥有效应力系数,无量纲;E是杨氏模量,MPa;εH,εh分别为最大与最小水平(构造)应变,m/m;ν是泊松比,无量纲。
从上述两式可以看出,水平主应力由3部分组成:公式(1)和(2)右侧的第一与第二项是由垂向应力和地层压力造成的,而右侧的第三项是由构造应变导致的。由于构造应变较难定量确定,一些简化的方法可以用于预测水平主应力[13-14]。公式中的泊松比、比奥有效应力系数和杨氏模量可以通过测井数据计算得到。因此,当垂向应力、地层压力和构造应变已知时,最大与最小水平主应力可以通过上述公式得到。由于公式中有些参数难于准确确定,造成水平主应力评价的误差与不确定性,因此,预测的水平主应力需要应用观测数据进行校正。
1.2 地应力实测结果
1.2.1 垂向应力
垂向应力是由上覆岩层的重量导致的应力,可以通过积分密度测井数据得到。通过分析新场气田和合兴场气田的几十口井的密度测井数据,得到了如下的垂向应力预测公式:
σV=0.024 6Z
(3)
式中:Z是深度,m。
1.2.2 最大与最小水平主应力
为了获得水平主应力,首先需要确定地层压力。本研究根据实测的储层压力结果和钻井中的溢流、井涌和测井数据得到了新场及其周围气田地层压力[15-16]。另外,利用观测数据分析了最大与最小水平主应力,包括应用测试压裂数据、应变实验数据,以及利用成像测井中的井壁崩落与井壁诱导张裂缝数据(表1,表2)。图1为数10口井实测的不同地层的地层压力、最小水平主应力、垂向应力和据这些实测数据计算的可靠的最大水平主应力。可以看出,实测的地层压力和地应力有如下的特点。
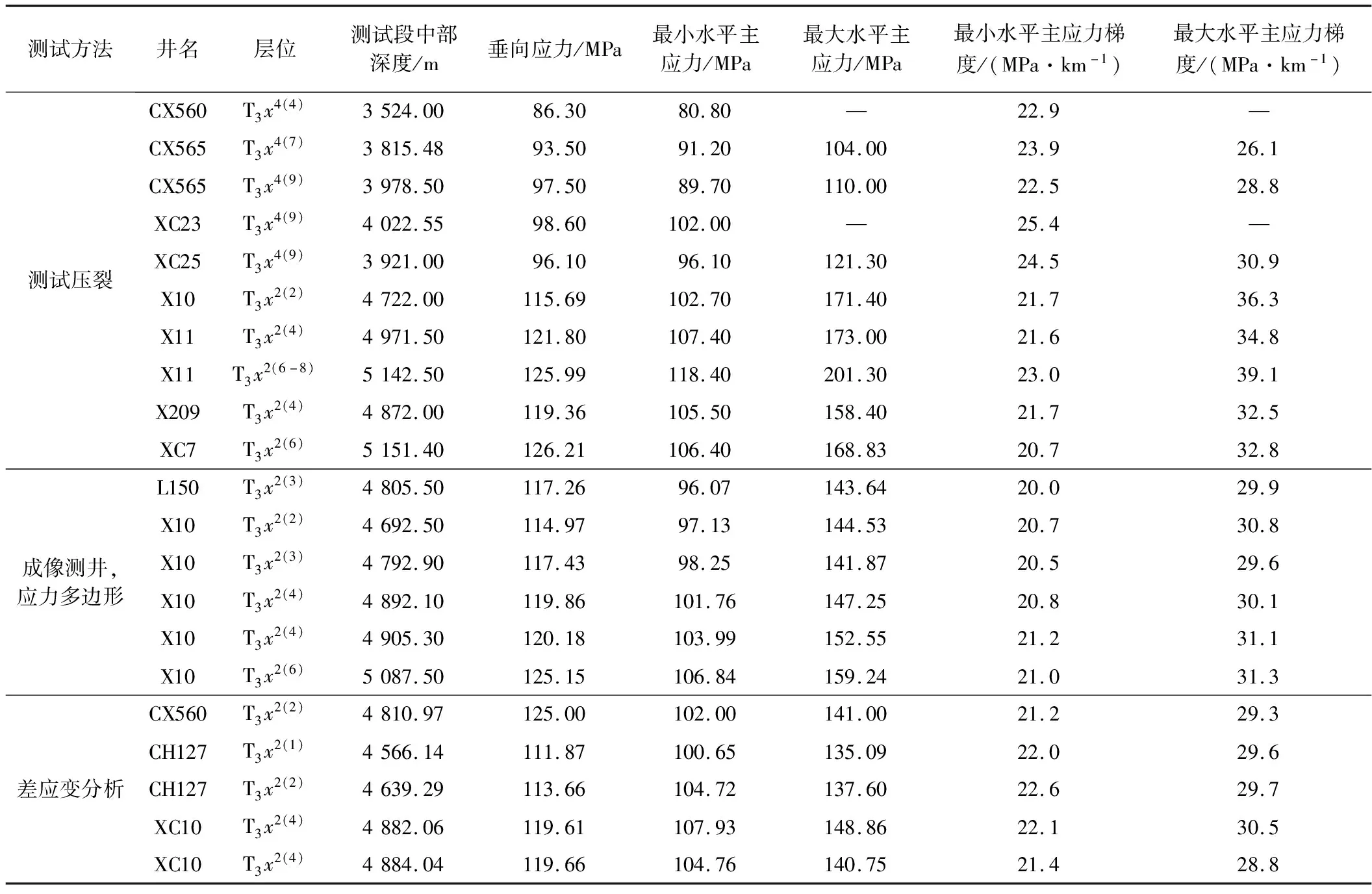
表2 不同测试方法得到的四川盆地川西坳陷须二段和须四段的水平主应力
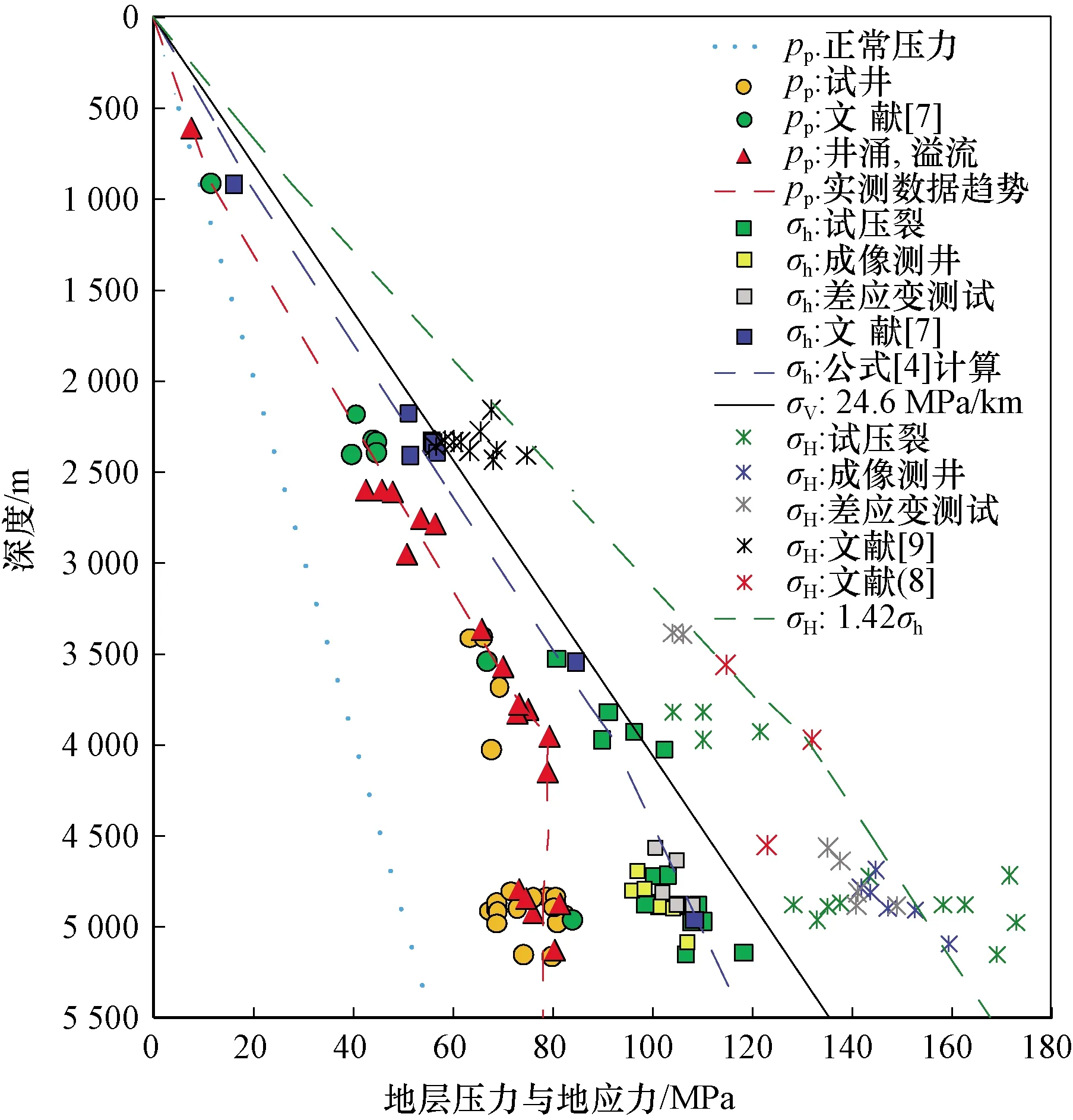
图1 据实测数据得出的四川盆地川西坳陷须家河组与侏罗系岩层的地层压力与地应力
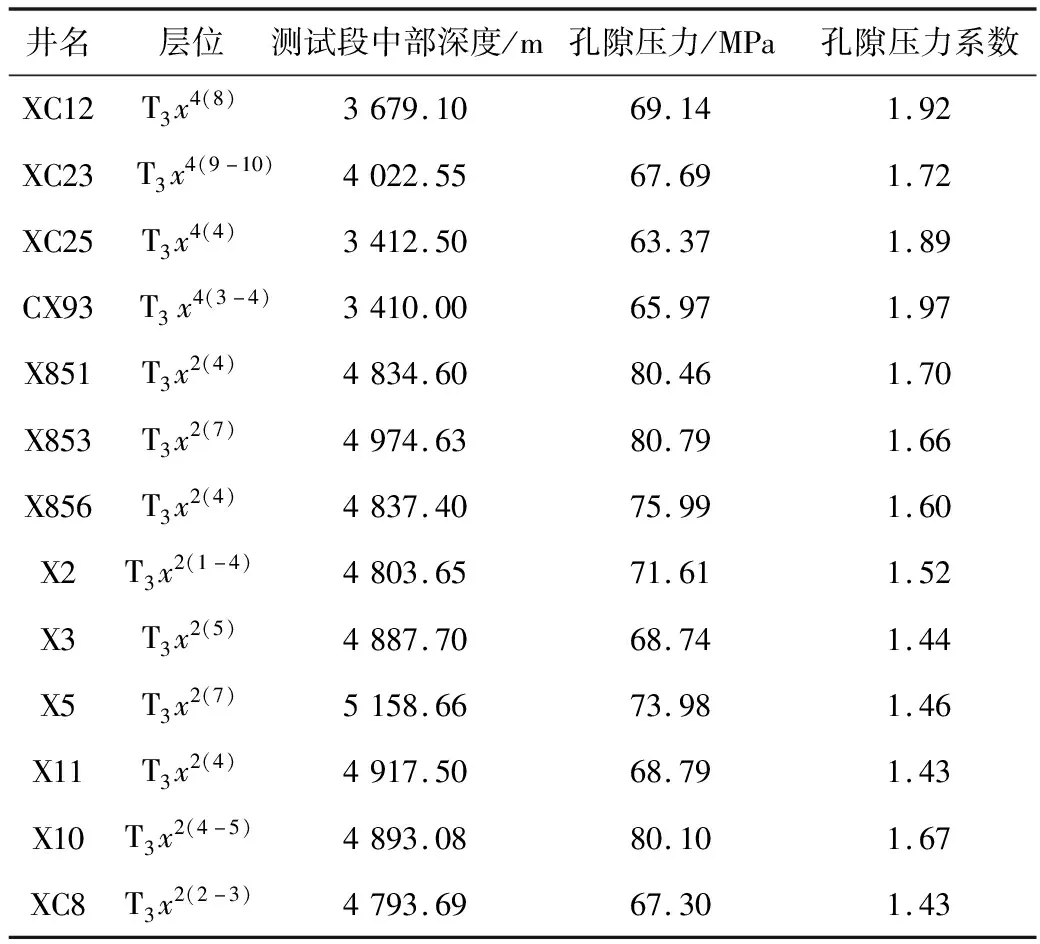
表1 通过压力恢复试验得到的四川盆地川西坳陷须二段和须四段孔隙压力
1)地层压力(pp)远远高于静水压力,其与深度(Z)成线性关系增加,即从埋深600 m开始的侏罗系至三叠系须四段(至埋深约4 000 m处):pp=0.021 3Z-5.33。
2)须四段具有很高的地层压力梯度(20 MPa/km)。但从须四段底部至须二段储层,地层压力梯度大幅度降低。须二段具有较小的地层压力梯度(15.6 MPa/km),从而造成其最小水平主应力梯度降低。
3)从侏罗系、须五段至须三段最小水平主应力与垂向应力接近(σh≈σV<σH)。最小水平主应力梯度很高,约为24 MPa/km。地应力处于走滑断层至逆断层应力状态,据此推测,压裂裂缝形态可能处于水平缝与垂直缝之间,即具有一定倾角的裂缝。
4)须二段岩层的最小水平主应力小于垂向应力(σh<σV<σH),处于走滑断层应力状态。但是最小水平主应力梯度仍然较高,约为22 MPa/km。与须四段相比,须二段具有有利的应力状态,压裂能够产生垂直裂缝。
5)最大水平主应力大于垂向应力。最大水平主应力可近似地用下式来描述:σH=1.42σh。
根据实测数据,得出了本研究区砂岩的最小水平主应力预测的经验公式:
σh=k0(σV-pp)+pp
(4)
式中:k0为取决于岩性和构造应力的系数,无量纲,在本研究区域k0=0.7(图1)。
比较公式(4)与公式(1),可以得到以下较通用的公式用于预测本区各向同性岩层的最小水平主应力:
(5)

当地层压力已知时,可以使用公式(5)结合公式(3)估计最小水平主应力,但是此方法仅适用于各向同性的岩层。从图1可以看出,实测的最大与最小水平主应力较发散,尤其是在须二段砂岩。其原因可能是一些储层含有天然裂缝而导致岩层各向异性。例如,须二段砂岩的优质储层中常含有高角度或垂直裂缝。从须二段砂岩露头、成像测井及岩心中可以看出,岩层中发育着近似相互平行的垂直裂缝,此类储层是本地区产量最高的储层(图2a)。这种储层可用横向各向异性-纵向各向同性(HTI)模型模拟。但是,一些须二段储层中也含有水平或低角度裂缝(图2b),属于较差的储层。这种储层可以用纵向各向异性-横向各向同性(VTI)模型来模拟。

图2 四川盆地川西坳陷须二段砂岩天然裂缝发育野外照片
2 须家河组储层各向异性地应力模型
考虑到须家河组储层中天然裂缝的赋存状态不同,有些岩层中发育着近似相互平行的垂直裂缝,而另一些储层中则含有水平裂缝,因此,下面将分析这两种不同的模型(VTI和HTI)。当岩层中发育着倾斜裂缝时,结合VTI和HTI两种模型可以得出用于预测不同裂缝倾角条件下地应力的通用方法。
2.1 纵向各向异性横向各向同性岩层的水平主应力
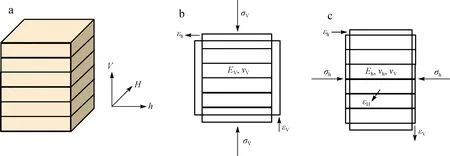
沉积地层一般为层状的岩层,层与层之间发育层理。这种岩层一般沿横向为各向同性,而沿纵向为各向异性。这类岩层可以应用纵向各向异性-横向各向同性(VTI)介质理论来模拟(图3a),例如页岩层和其他薄层沉积岩。对于VTI地层,其对称轴是垂直方向,而对称面是水平面;在水平方向上岩石性质相同,而在垂直方向上则不同。VTI地层的最小和最大水平主应力可以通过下列公式得到[12,17-18]:
(6)
(7)
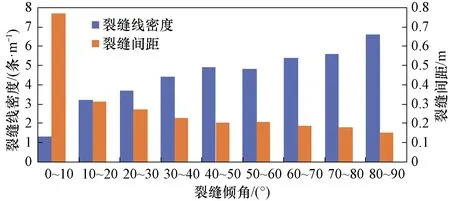
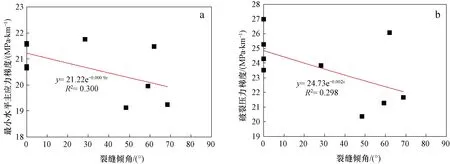
式中:σh,VTI,σH,VTI分别是VTI岩石的最小和最大水平主应力,MPa;Eh和EV为水平与垂直方向的弹性模量,MPa;νh和νV为水平与垂直方向的泊松比,无量纲;αh和αV为水平与垂直方向的比奥有效应力系数,无量纲。其中EV 图3 四川盆地川西坳陷VTI各向异性地应力模型 对于VTI介质,岩体的弹性模量(EV)与岩石的弹性模量(Eh或E)可以用下面的公式来估算[21]: (8) (9) 式中:A为弹性模量各向异性参数,无量纲。从上可知,A>1,并且A随裂缝密度增加而增大。将参数A和νh=ν代入公式(6),如果假设αh=αV可以得到简化的VTI岩层的最小水平主应力: (10) 式中:CV为VTI岩层泊松比各向异性参数,无量纲。CV=ν/νV>1。kn越大,CV越小,则σh,VTI越大;n越大,CV越大,则σh,VTI越小。而kn越大,A越小,则σh,VTI越小;n越大,A越大,则σh,VTI越大。因此,岩层各向异性的两个参数A和CV对弹性模量和泊松比的影响相反,导致对σh,VTI的影响也相反。 公式(10)与各向同性岩石的最小水平主应力公式(1)所不同的只是第一项中的两个参数,而构造应力项与各向同性条件下的相同。 根据公式(5),对于须家河组的VTI岩层,公式(10)可以简化成下式: (11) 横向各向异性-纵向各向同性(HTI)是描述在各向同性岩石中分布着一组相互平行的垂直裂缝所构成的各向异性岩体模型。这种岩体的各向同性面为垂直面。对于须家河组储层中含有一组相互平行的垂直裂缝的岩体,可以使用HTI模型来描述(图4a)。根据正交各向异性岩体的应力应变本构关系[20],推导出了下列用于计算HTI岩层的最小和最大水平主应力的理论公式: (12) (13) 式中:σh,HTI,σH,HTI分别是HTI岩层的最小和最大水平主应力,MPa;每个弹性模量和泊松比的符号意义见图4b—d;νVh,νVH为垂直方向的泊松比,无量纲;νhV为水平方向的泊松比,无量纲;并且νhV/Eh=νVh/EV,νVH=ν。因此公式(12)和(13)共有4个独立的杨氏模量和泊松比。值得注意的是,最小水平主应力应该出现在垂直裂缝的走向方向,而最大水平主应力应该在平行裂缝的走向方向(图4a)。 图4 四川盆地川西坳陷含垂直裂缝各向异性HTI岩层和在不同方向加载可以得到的岩层弹性力学参数 与VTI岩层相反,HTI岩层具有Eh (14) 因此,对于HTI岩层, (15) 因为在HTI岩石中νVH=ν,νVh>νVH>νhV,所以可以假设νVhνhV≈ν2。另外,如果假设αh=αV,式(12)可以近似写成下式: (16) 式中:CH为HTI岩层泊松比各向异性参数,无量纲。CH=νVh/ν>1;kn越大,CH越小,则σh,HTI越小;而n越大,CH越小,则σh,HTI越大。与杨氏模量有关的各向异性参数A=EV/Eh>1。并且kn越大,A越小,则σh,HTI越大;而n越大,A越大,则σh,HTI越小。裂缝的两个参数CH和A对弹性模量和泊松比的影响相反,导致对σh,HTI的影响也相反。 比较公式(16)与公式(1)可以看出,与各向同性岩石所不同的是HTI的第一项和第三项中的两个系数A和CH。如果A=CH,则从公式(16)与公式(1)可知,HTI岩层比各向同性岩层具有更小的最小水平主应力。这说明含垂直或高角度裂缝岩层可能具有更小的最小水平主应力,小于各向同性岩层和含水平裂缝(VTI)的岩层。 同样可以得到简化的最大水平主应力计算公式: (17) 比较式(16)与式(2)可知,HTI岩层与各向同性岩层具有很相近的最大水平主应力。 根据公式(5),对于须家河储层的HTI岩层,最小水平主应力公式(16)可以简化成下式: (18) 对于研究区的储层,如果天然裂缝组为水平裂缝,则可以应用VTI模型来预测地应力。如果天然裂缝组为垂直裂缝,则可以用HTI模型来预测地应力。但是,当天然裂缝为倾斜裂缝时上述的两种模型均不适用。下面将给出倾斜裂缝的解决方法。考虑到储层中的天然裂缝可能是倾斜裂缝,下面给出一个通用的模型来预测裂隙岩层的水平主应力。考虑到当裂缝倾角从0°~90°变化时会导致岩体由VTI逐渐转化成HTI介质。如果假设这种转化服从线性关系,则结合公式(11)和(18)可以得到下面的近似公式,用于计算随裂缝倾角的变化而变化的各向异性岩体的最小水平主应力: (19) 天然裂缝造成岩体各向异性。前述的各向异性理论表明,对于含高角度裂缝的岩体,水平主应力随裂缝密度的增加而减小。由14口井成像测井解释的须二段裂缝数据表明(图5),裂缝的密度随裂缝倾角的增加而增大,高角度(80°~90°)裂缝的密度很大,为6.6条/m。在其中的10口井中既有最小水平主应力和破裂压力观测数据又有成像测井裂缝密度等数据,图6为这10口井的最小水平主应力梯度和破裂压力与天然裂缝密度的关系。图5是须二段所有成像井解释得到的天然裂缝线密度统计,而图6统计的是须二段内既做过成像解释又做过压裂改造层段的天然裂缝线密度统计,往往这些压裂改造层段内的天然裂缝并不很发育。从图6a可以看出,最小水平主应力梯度总体上随着裂缝密度的增大而减小,这与HTI模型的结论相同。从图6b可知,破裂压力梯度随着裂缝密度的增大而减小。从图7a可以看知,最小水平主应力梯度总体上随着裂缝平均倾角的增大而减小。这符合HTI的规律。这是因为当裂缝倾角增大时,各向异性岩体更接近HTI介质,所以最小水平主应力梯度减小。图7b显示,破裂压力梯度随着裂缝平均倾角的增大而减小。虽然图7中数据点较分散,相关系数较小,但是仍显示出一定的规律。如果将图7a中的横坐标更换为裂缝倾角最大值后,相关系数得到改善,这表明裂缝最大倾角对地应力的影响也较大。 图5 四川盆地川西坳陷14口井中须二段储层成像测井得到的裂缝密度和裂缝间距与裂缝倾角的关系 图6 四川盆地川西坳陷10口井中须二段储层成像测井得到的裂缝线密度与最小水平主应力梯度(a)和破裂压力梯度(b)的关系 图7 四川盆地川西坳陷须二段储层成像测井得到的裂缝倾角与最小水平主应力梯度(a)和破裂压力梯度(b)的关系 图6b和图7b说明具有高密度和高角度的天然裂缝岩层具有更小的破裂压力,由此推断应该更易压裂。图7a显示高角度天然裂缝可以导致最小水平主应力梯度降低约2 MPa/km。岩层的破裂压力梯度也有同样的规律:天然裂缝可以导致破裂压力梯度降低约4 MPa/km,或导致破裂压力在埋深5 000 m时降低20 MPa。另外,实测数据还显示最小水平主应力梯度和破裂压力梯度随着裂缝指示因子的增大而减小。 当各向异性岩石的杨氏模量与泊松比已知时,可以代入前面得出的相关公式获得各向异性岩层的最小水平主应力。如果天然裂缝为水平裂缝,则可以用VTI模型,即公式(10)或(11),来预测最小水平主应力。如果天然裂缝为垂直裂缝,则可以用HTI模型,即公式(16)或(18),来预测最小水平主应力。如果岩层中天然裂缝为倾斜裂缝,当裂缝的倾角已知时,可以应用公式(19)计算随裂缝倾角不同而变化的各向异性岩体的最小水平主应力。当岩石各项异性参数难于获得时可以采用以下的经验公式估算须家河储层各向异性裂隙岩层的最小水平主应力。 根据实测的天然裂缝与地应力数据可以得出本研究区的经验公式。如果假设没有天然裂缝存在时的最小水平主应力为σh,则当裂缝存在时,最小水平主应力可以从图6a和图7a实测数据的回归关系获得: σh,f=e-0.037nσh (20) σh,f=e-0.000 9βσh (21) 式中:σh,f是有裂缝时的最小水平主应力,MPa;n是裂缝线密度,条/m;σh是没有裂缝时的最小水平主应力,可以从式(5)获得。 同样从图6(b)和图7(b)中可得到含天然裂缝岩层的破裂压力: pb,f=e-0.088npb (22) pb,f=e-0.002βpb (23) 式中:pb,f是含有天然裂缝时的破裂压力,MPa;pb是没有裂缝时的破裂压力,MPa,可以从文献[6]获得。 因此,对于含天然裂缝的岩层,可以应用理论模型,公式(19),结合经验公式(20)或(21)来评价各向异性岩体的最小水平主应力。图8为其中的一个应用案例,在此案例中根据X10井的测井(包括成像测井)数据解释了天然裂缝倾角,并据此计算了天然裂缝对最小水平主应力的影响。图8a的自然伽马测井数据显示在4 877~4 887 m井段为10 m厚的须二段砂岩,其中一些岩层含有高角度天然裂缝(图8b)。根据公式(5)和测井声波时差得出的泊松比与c=0.45,计算了各向同性条件下的最小水平主应力,之后根据经验公式(21)计算了天然裂缝导致的最小水平主应力(图8c)。假设A=1.438,CH=CV=1.37,c=0.45,根据各向异性应力公式(19)计算了天然裂缝引起的最小水平主应力变化。图8c比较了本文提出的各向异性模型的计算结果与据观测数据得出的各向同性岩层的经验公式和裂隙岩层经验公式的结果。从图8c可以看出,各向异性模型的公式(19)和裂缝倾角经验公式(21)得出的最小水平主应力结果相一致。本研究将此评价方法应用到了其他的几口井,取得了同样的结果,这说明各向异性模型可以用于预测本区的最小水平主应力。应用结果还表明(图8c),高角度裂缝的存在造成岩层的最小水平主应力梯度降低,降低的幅度可达6%,这将有利于储层的压裂改造。实验结果证实了此结论,室内须家河组露头水力致裂模拟表明,含高角度裂缝的岩心破裂压力降低幅度达8.1%~26.9%。因此,对于裂隙岩层,在进行地应力预测时需要考虑各向异性对水平主应力的影响,并且据此得出破裂压力以用于压裂设计与施工。 图8 四川盆地川西坳陷X10井中应用不同方法计算的最小水平主应力 1)数据显示,从侏罗系、须五段至须四段最小水平主应力梯度逐渐增加,最小水平主应力与垂向应力相近。地应力处于走滑断层至逆断层应力状态,据此推测,压裂裂缝形态将处于水平与垂直之间。而须二段储层处于走滑断层应力状态,最小水平主应力小于垂向应力。与须四须段相比,须二段具有较好的应力状态。压裂能够产生垂直裂缝。 2)各向异性的VTI岩层比各向同性的岩层具有稍高的最小水平主应力,这表明层状岩层(含软弱层理)或含水平裂缝的岩层具有稍高的水平主应力。 3)一般情况下,各向异性的HTI岩层比各向同性岩层具有更小的最小水平主应力,这说明含垂直或高角度裂缝的岩层具有较小的最小水平主应力,即小于各向同性岩层和含水平裂缝(VTI)的岩层。这类岩层较易于压裂。须家河的实测数据与这一规律吻合。文中结合VTI和HTI两种模型提出了用于评价不同裂缝倾角时裂隙岩层水平主应力的方法。 4)实测数据表明,最小水平主应力和破裂压力随着裂缝密度、裂缝倾角和裂缝指示因子的增大而减小。天然裂缝可以导致最小水平主应力梯度降低约2 MPa/km,导致破裂压力降低约4 MPa/km。 5)天然裂缝造成岩层各向异性,降低了须家河组部分储层的压裂难度。如果采用物探和测井的方法估算出储层各向异性的区域,将有望找出易于压裂的有利生产区。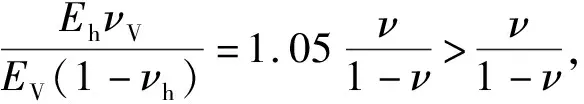

2.2 水平各向异性-纵向各向同性岩层的水平主应力



2.3 结合VTI和HTI的裂隙岩体水平主应力模型
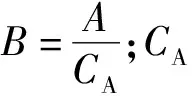
3 须家河组储层地应力的影响因素与水平主应力预测
3.1 天然裂缝对水平主应力和破裂压力的影响

3.2 各向异性裂隙岩层水平主应力的预测

4 结论

