扭转陀螺的动力学研究*

张雷明，寻之朋，张 伟

(1.中国矿业大学徐海学院，江苏 徐州221008;2.中国矿业大学 材料与物理学院，江苏 徐州221116)

2017年中国大学生物理学术竞赛[1-3]中，第12题是将轮子的轴固定到具有一定抗扭力的垂直线上，要求在扭转线和旋转轮子并释放后，对这个系统进行动力学研究。为此，我们制作了一个实验装置，如图1所示。如果静止时将轮子放开，轮子受到的重力相对于竖直旋转轴产生力矩，方向如图2所示，这个力矩使系统沿力矩方向产生角动量，将要求整个系统逆时针方向旋转，则轮子会侧翻[4-5]。如果把轮子转动后再放开，由于轮子已经有了一定的初始角动量，在力矩的作用下，轮子会以悬挂轮子的垂直线为轴扭转。本文主要对轮子围绕垂直线扭转时的动力学性质进行理论分析和实验研究。首先基于拉格朗日方程[6]从理论上推导轮子运动过程中进动角α所满足的变化关系，然后在不同实验条件下对进动角的变化进行实验测量，最后将实验结果和理论结果进行比较发现理论分析与实验相符合，从而得出有意义的结论。

图1 实验装置

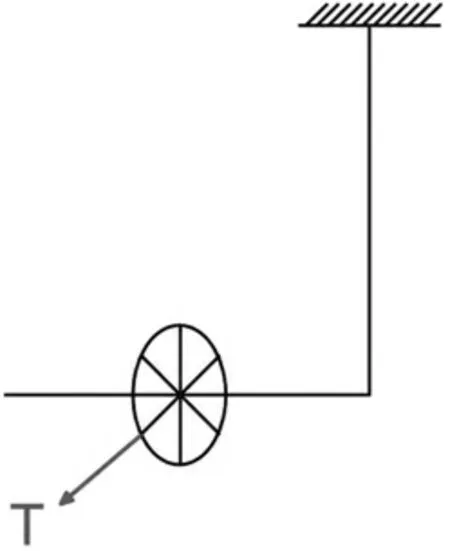
图2 实验装置示意图

1 理论分析

在本部分，从理论上推导把轮子转动后放开以垂直线为轴扭转过程中进动角和章动角的变化关系。如图3所示，考虑绳子无扭转力的情况下，对轮子系统建立惯性坐标系Oxyz和固连坐标系Ox′y′z′和Ox″y″z″，并定义绕自转轴的转动惯量为Jx，绕赤道轴的转动惯量为J，列出系统的动能为[6]

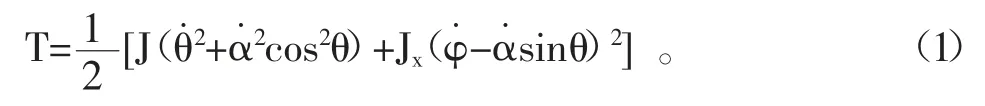
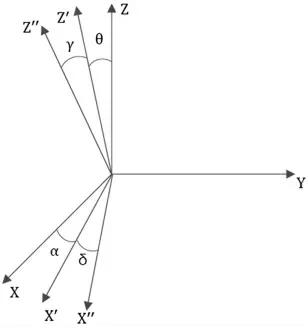
图3 坐标系

将系统的拉格朗日方程对x、y、z轴分解，得

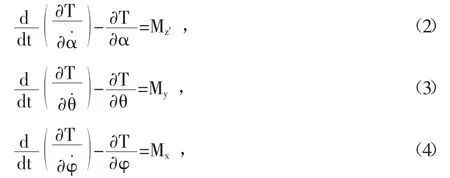
其中Mz′、My、Mx为轮子受到的力矩沿Oxyz轴系的投影。联立(2)、(3)、(4)式解得

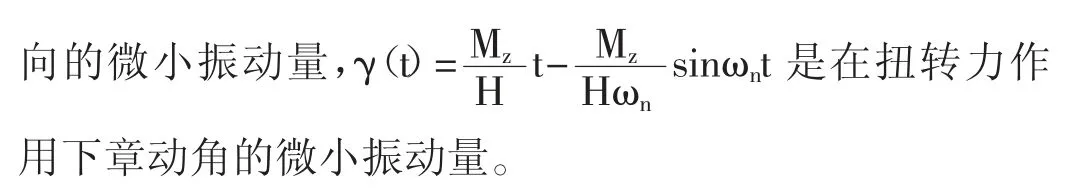
2 实验研究

这一部分主要是对把轮子转动后放开绕垂直线扭转运动过程中的动力学性质进行实验观测。使用的实验器材有不同材质不同长度的绳子和材料、大小、粗细不同的轮子，驱动装置由变压器、电动机和信号接受装置组成，使用的测量仪器由JY-901模块传感器、ZG-2型转动惯量测量仪、周期测量仪和游标卡尺等组成。测量工作主要有四个方面：

(1)测量轮子以不同的速度转动时，进动角随时间变化的数据，如表1所示。

根据表1中的数据，可画出一样大小的两个轮子以不同转速运动时进动角α的实验值随时间的变化曲线，分别如图4和图5所示。

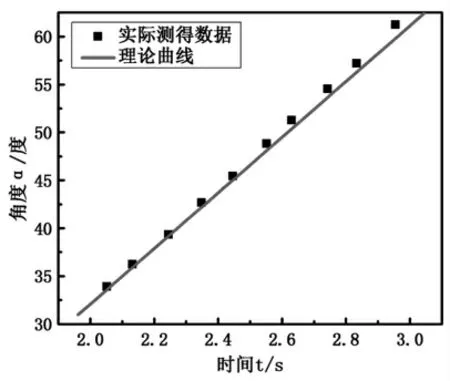
图4 小轮子转速n=4.3转/s时进动角变化曲线

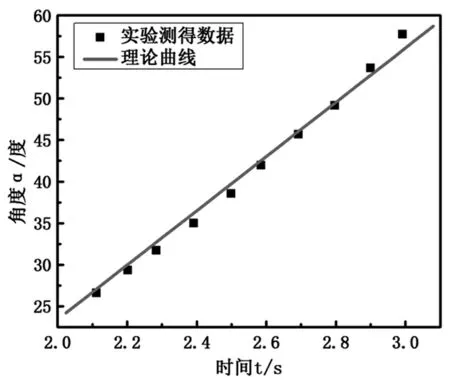
图5 小轮子转速n=3.7转/s时进动角变化曲线

表1 不同转速下进动角随时间变化测量值

从图中可以看出，实验曲线和理论曲线基本吻合。同时，利用实验曲线得到转速n=4.3转/s和n=3.7转/s时(13)式中的比例系数K的值分别为K=29.3和K=32.6，表明进动角α的变化快慢与轮子的转速成反比，这一结论与理论分析结果是一致的。因此，我们对轮子转动后放开绕垂直线扭转过程中的动力学分析是合理的。

(2)测量不同半径的轮子转动时，进动角随时间变化的数据，如表2所示。

表2 轮子半径不同进动角随时间变化测量值

利用实验数据可拟合出半径r=15.18cm和r=20.54cm的轮子以相同转速运动时进动角α随时间变化的曲线，如图6和图7所示。根据实验曲线计算得到曲线斜率分别为K=29.3和K=16.3，说明轮子半径越大，曲线斜率越小，角速度越小。由理论分析建立的(13)式也有同样的结论。对轮子的理论分析和实验相符合，说明我们成功地解释了轮子转动后放开绕垂直线扭转过程中的动力学过程。

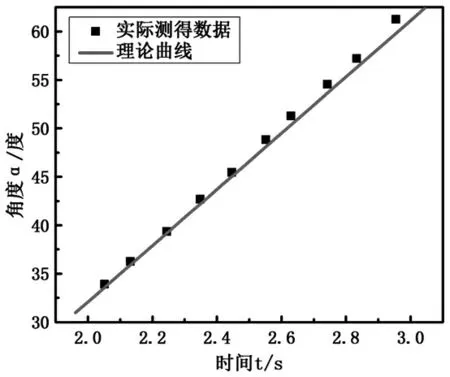
图6 半径r=15.18cm的轮子进动角变化曲线

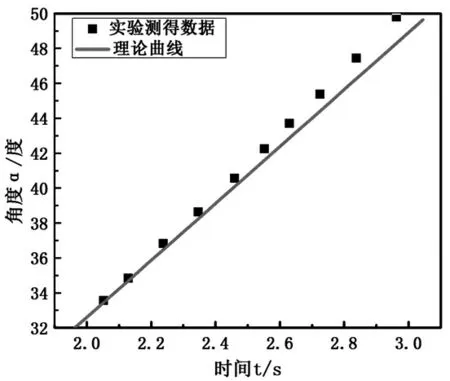
图7 半径r=20.54cm的轮子进动角变化曲线

(3)测量悬点到转轴距离不同时，进动角随时间变化的数据，如表3所示。

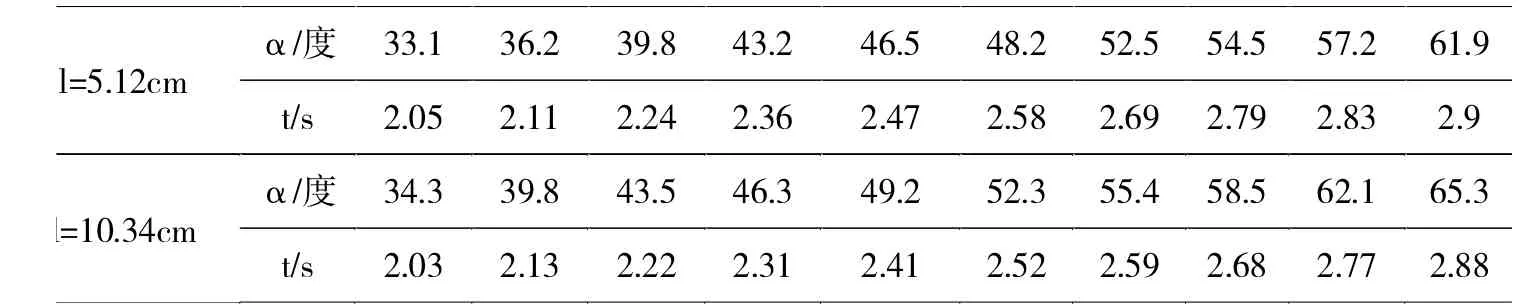
表3 悬点到转轴距离不同时进动角随时间变化测量值

表3给出了半径相同的轮子悬点到转轴距离为l=5.12cm和l=10.34cm运动时进动角α随时间变化的数据，变化曲线分别如图8和图9所示。

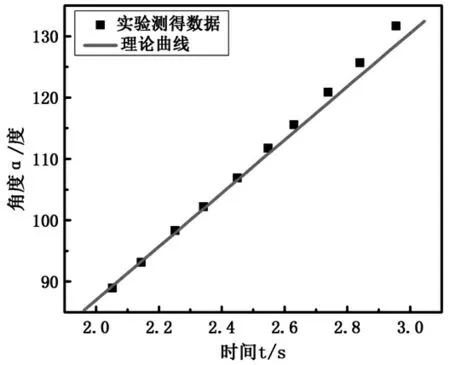
图8 小轮子悬点距离l=5.12cm时进动角变化曲线

根据实验数据计算得到悬点到转轴距离为l=5.12cm和l=10.34cm时曲线的斜率分别为K=29.3和K=43.5，说明悬点到转轴的中心距离越大进动角α变化越快，和通过理论分析建立的(13)式得到的结论是一致的，图8和图9中实验曲线和理论曲线基本吻合也充分说明了这一点。

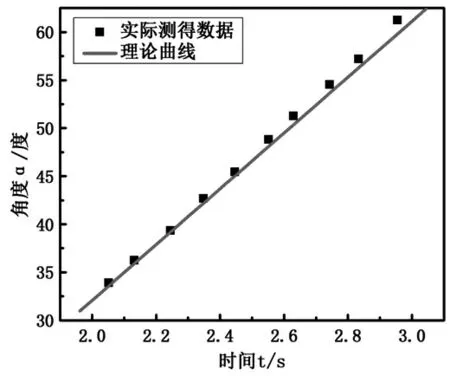
图9 小轮子悬点距离l=10.34cm时进动角变化曲线

(4)如果考虑轮子长时间转动，则转速随时间衰减，图像曲线的斜率应该不断增大。实验测量曲线如图10所示，结果显然与理论相符。

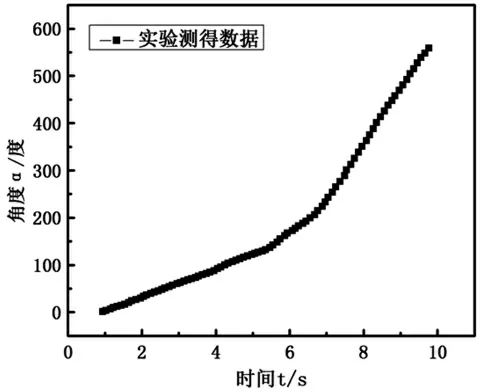
图10 长时间转动进动角变化曲线

3 结论

本文制作了扭转陀螺模型，将轮子的轴固定到具有一定抗扭力的垂直线上，先把绳子扭转和让轮子绕轴旋转，然后将系统释放，对系统的动力学性质进行理论分析和实验研究。首先利用拉格朗日方程从理论上推导得到轮子运动过程中进动角的变化关系，发现影响进动角变化快慢的因素主要有轮子的初始转速、半径和绳子悬点到轮子转轴的距离。接着在不同条件下对进动角的变化进行实验测量，比较发现实验计算结果与理论分析结果是一致的，即短时间内，进动角的变化快慢与轮子转速成反比、与轮子半径平方成反比、与绳子悬点到轴的距离成正比。实验研究还表明，如果轮子长时间转动，则转速随时间衰减。