基于多特征与改进卷积神经网络的AGV实时调度研究

卜人杰，朱 瑾

（上海海事大学 物流科学与工程研究院，上海 201306）

0 引言

AGV具有自主定位、自主导航、信息交互等特点，结合AGV实时数据信息的优化调度可以有效降低集装箱的周转时间和作业成本[1,2]。

目前针对AGV的调度研究一般在已知集装箱作业任务信息的前提下，用启发式算法求解[3,4]，但是这种传统的优化方法不能满足自动化码头动态变化的情况。因此近年来，基于机器学习的实时动态调度方法日益受到重视，通过真实数据或模拟仿真学习各个状态的最优策略[5]。目前神经网络被广泛应用于分类、聚类、数据处理等方面[6]。解明利等[7]提出了一种基于最大熵的神经网络权值优化算法，解决了传统神经网络在进行调度策略时易陷入局部最优的问题。Akyol等[8]提出了一种基于神经网络的决策系统，通过仿真实验获取数据并训练神经网络，使得神经网络可以根据给定的参数选择最优的决策。Choe等[9～11]提出了一种在线学习指派策略，并以岸桥平均延迟时间和AGV空载距离最短为目标，使用BP神经网络训练两个集装箱之间的偏好强度，实现实时指派。但是BP神经网络中权值太多，计算量太大，需要大量样本进行训练，影响求解速率。Xin等[12]以装卸集装箱的总完工时间最少为目标，提出了一种基于当前状态的设备重调度方法。Ren等[13]采用强化学习算法，建立Q学习和离线学习模块，针对多种调度策略，在每次调度结束后，动态的给出下一状态的调度策略。但是使用非线性函数的强化学习往往会因为特征不同产生分歧，导致收敛性很差。因此可以利用卷积神经网络强大的特征学习能力，学习非线性模型并通过局部拟合学习得到实时模型，为了提高卷积神经网络的学习能力，主要是通过增加输出通道的数量，但是这会造成参数过多和过拟合。

综上所述，针对自动化码头AGV调度和卷积神经网络中存在的参数过多、过拟合等问题，考虑AGV的行驶速度，每个集装箱作业的紧急程度等约束，建立以岸桥（Quay Crane，QC）平均作业时间最短和AGV空载距离最小为目标的AGV实时调度模型，并设计了一种改进的一维卷积神经网络对实时调度指派策略进行在线学习，基于InceptionNet的一维卷积通过分支的方式增大网络的宽度和深度，去除了最后一层全连接层。确定了实验样本池容量，设计基于多特征在线学习指派策略与最短车程指派策略的对比实验，比较了不同规模的AGV在作业动态程度不同的情况下的QC平均作业时间、AGV空载距离和总完成时间。

1 多特征指派模型

1.1 模型假设

首先定义一个集装箱，当它需要QC进行装卸货并且还没有分配AGV时，那么这个集装箱就为候选作业，并作出以下假设：

1）一个岸桥对应多个堆场，AGV所服务的岸桥、场桥不固定；

2）AGV每次只运输一个集装箱；

3）所有集装箱作业计划已知；

4）当AGV无作业时回到中转区；

1.2 模型框架和变量设定

当AGV完成当前的作业，就会触发调度。第一步通过从每个QC的装载或卸货顺序中收集候选作业，在线学习算法会使用当前的调度策略从候选作业中选择一个作业，然后将该作业分配给请求新作业的AGV，当前调度策略从候选作业中选择的作业不一定是真正的最佳作业。特别是作业开始是以随机的初始策略开始。在第二步中，基于每个候选作业的多特征，通过短暂的超前模拟仿真个连续作业分配来评估每个候选作业，使用偏好函数检查所有候选作业的评估值来确定最佳作业，将最佳作业与其余每个作业配对形成训练样本，最后使用改进的卷积神经网络在线学习训练样本并更新指派策略在此仿真中，并将指派策略应用到下一次调度过程中。为了阐述模型，引用以下变量进行表示。其中流程图如图1所示。

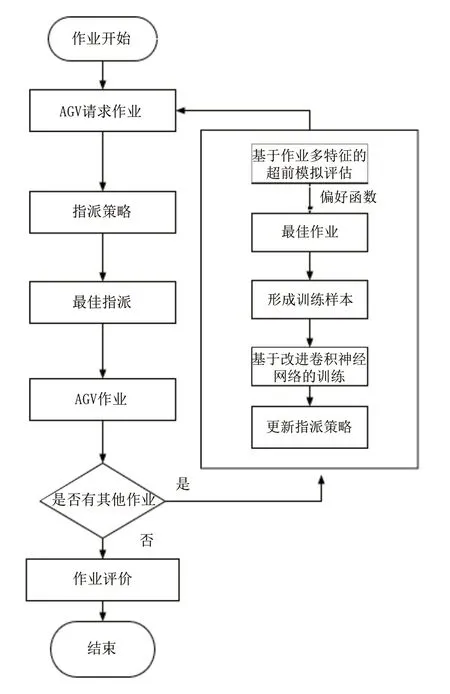
图1 AGV实时指派流程图

J为候选作业集；

π为指派策略；

T为样本池；

R为样本上限；

L为仿真模拟作业个数；

I为一个集装箱作业；

J*为最佳作业；

C为新生成的作业训练样本；

V为候选作业集合的评价数组；

ω为权重。

1.3 基于多特征的集装箱作业表示

在为AGV指派作业时，通过对候选作业的各种标准评估来选择最佳作业，其中一些标准是经过设计尽量减少AGV的空载距离和最小化QC的平均作业时间。本文使用7个状态来表示一个装卸船候选作业，如表1所示。每个标准将在下文进行详细描述。

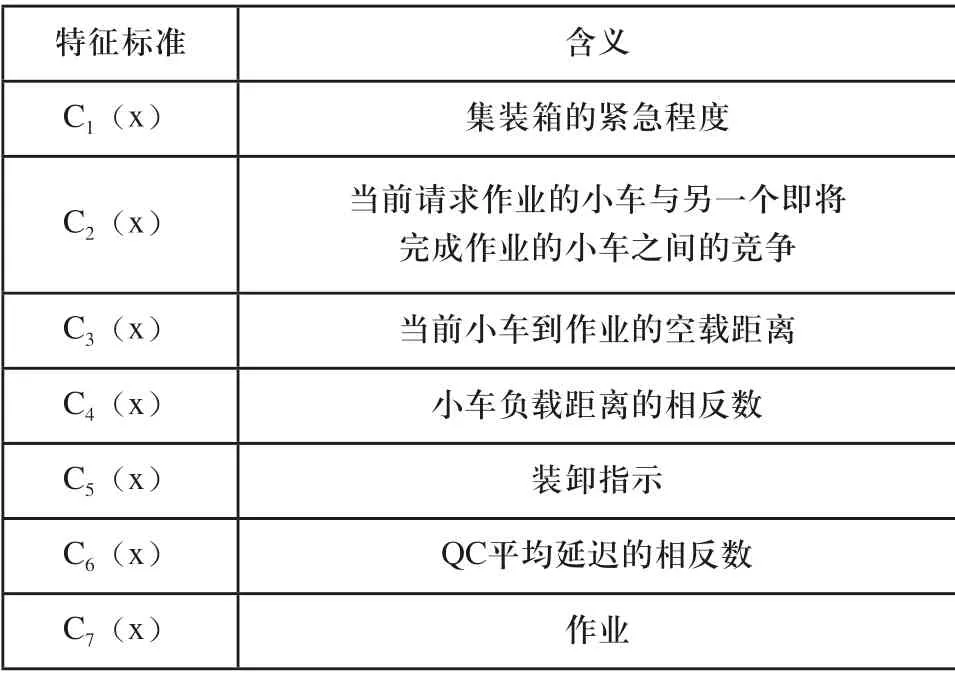
表1 候选作业特征指标

令X为候选作业的集装箱，然后基于d个不同的标准，根据X的评估结果来构建关于候选作业的d维向量，即：

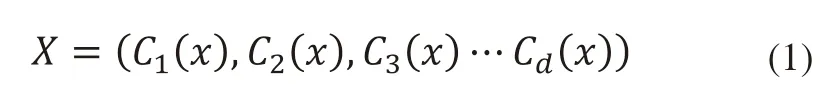
其中，Ci（x）是基于第i个标准的当前情况下的X的评估值。

C1（x）表示集装箱的紧急程度，即：

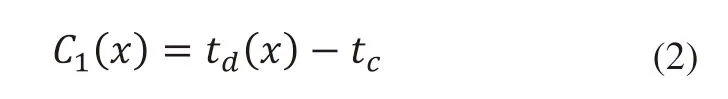
其中td（x）是AGV到达集装箱X的时间，tc为当前时间，C1（x）越小，表示该集装箱作业越紧急。

C2（x）表示当前小车到达集装箱X的时间与另一个最快完成作业的AGV到达时间之差，即：

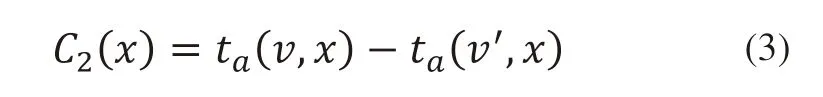
其中ta（v，x）为当前请求作业的AGV到达集装箱X的时间，x为请求作业的AGV到达集装箱X的空载距离，v'表示除了v以外另一个最快到达该集装箱X的AGV，此标准使得在做出调度决策时不仅考虑已经完成作业的当前AGV，还考虑了在不久的将来即将完成作业的其他AGV。

C3（x）表示当前请求作业的AGV到达集装箱X的空载距离。

C4（x）表示当前请求作业的AGV运输作业X的负载行驶距离的相反数。取相反数的目的是使分数变小，以获得更好的偏好。

如果是对集装箱作业X进行装船，则C5（x）=0，如果是对X进行卸船，则C5（x）=1，这表明该策略对于装船的偏好高于卸船，因为对于自动化集装箱码头，装载的效率是最重要的。

C6（x）表示QC平均延迟的相反数，即：

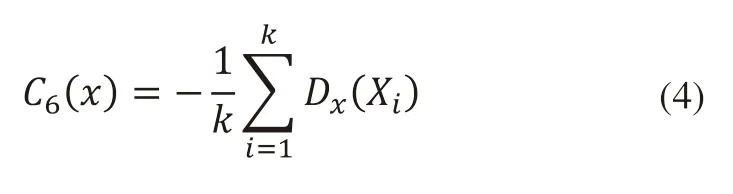
Dx（Xi）表示QC作业第i个集装箱所需要的时间，k表示到目前为止QC作业的集装箱数量。

C7（x）表示作业X的相对剩余工作负载，即：

其中Wx为存储当前作业X的堆场的集装箱数量，Wavg表示所有堆场中的平均剩余集装箱数量，C7（x）给予装载集装箱更高的优先级，当工作负载平均分配时，该值为-1/2，对于集装箱卸船作业时，该值固定为-1/2，C7（x）有助于均衡各个堆场间的集装箱数量。

使用以下归一化函数对上述7个指标特征进行归一化处理，处理为[0，1]中的值。

2 在线学习算法

2.1 偏好函数与目标函数

对于一对候选作业Xi和Xj，它们之间的偏好函数用式(7)表示，结果为[0，1]之间的实数，即：

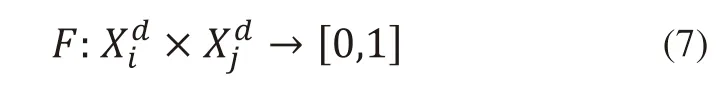
返回值接近于1表示第一个候选作业对第二个的偏好更高，当给出k个不同的候选作业时，可以将成对的偏好函数应用于每个可能组合的候选作业对来确定最佳作业。利用式(8)求出候选作业Xi在状态θ下的候选作业集合中的偏好之差总和。v（Xi|Jθ）值最大的作业Xi是当前候选作业集Jθ中的最佳作业J^*，因此对于一个给定的状态θ下的候选作业集Jθ中的指派策略π为式(9)所示。

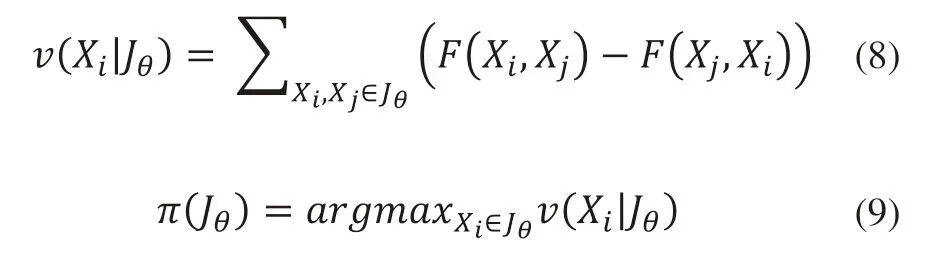
在实验中要实现的两大目标即：最大程度减少QC的平均作业时间和AGV的空载距离，我们应在此方面衡量调度决策的优劣，选择Tn和Dn最小作为评价指标建立目标函数f（n），假设已使用该调度策略处理了n个集装箱作业，使用目标函数(10)来衡量该调度决策的性能。

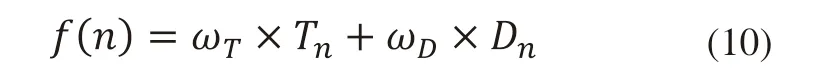
其中Tn表示QC处理n个集装箱的平均作业时间，Dn表示AGV运输n个集装箱的平均空载距离，ωT，ωD分别为各自的权重。这里Tn和Dn的计算方式如下：

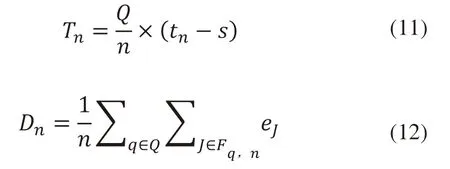
其中Q为QC的集合，tn为当第n个作业完成时，QC的作业时间，s是所有作业的开始时间，Fq，n是到时间tn为止时QC完成的作业集合，eJ是作业J的AGV的空载距离。ωT，ωD可以根据两个目标的相对重要性而发生变化。

2.2 样本的训练与评价函数

每次使用基于上述偏好函数的调度策略将集装箱作业分配给AGV之后，都会更新偏好函数以用于下一轮集装箱作业分配。即每完成一次调度决策，都会进行一次短暂的超前模拟评估每个候选作业，假设仅在k个候选作业中进行作业分配，把k中的每一个作业都作为一次最佳作业，然后进行模拟仿真，在这个过程中指派规则ω不变，在超前模拟仿真k个候选作业后，使用以下目标函数进行候选作业的评估，并得到一个评价矩阵，找出评价矩阵中评价函数最小的初始作业。在第一次AGV指派时，由于没有样本进行学习，我们是采用随机策略来进行训练样本的获取。

超前模拟仿真过程中的评价函数如下：

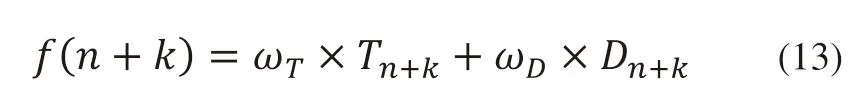
其中Tn+k和Dn+k的计算方式如下：

在洋葱的种植基地内，要严格进行管理，禁止对于高毒、剧毒或者高残留农药的使用，同时还需要禁止除草剂的使用。在种植过程中，应当选择抗病虫害能力较强的品种，减少使用化学药剂处理种子的操作。并针对种子的生长发育进行科学的田间管理。

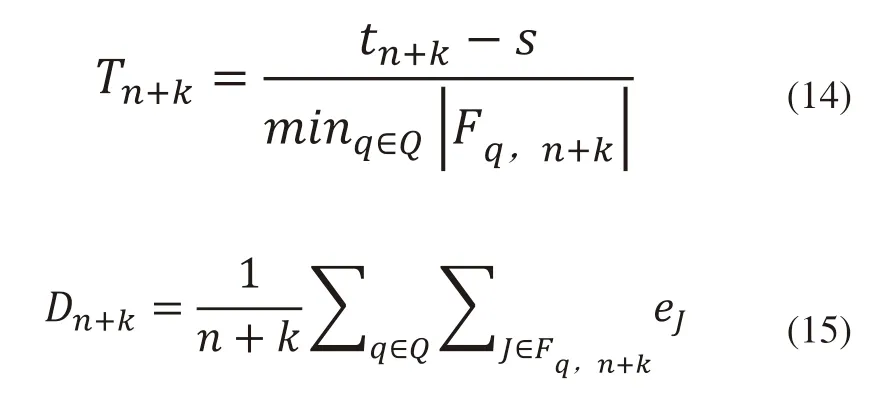
Dn+k的计算方式与Dn相同，但是Tn+k是通过计算处理集装箱作业数量最少的那个QC的平均作业时间来获得的，因为如果在短期的超前模拟仿真中使用式(11)来计算，则会使得QC首先去处理那些作业时间较短的集装箱，以得到较小的QC平均作业时间，但是这种对具有较短时间作业的偏向会使得具有较长处理时间的集装箱作业直到最后才会被选择，最终会导致分配这些作业的QC的延迟。所以采用式(14)来评估会促使所有QC的作业进度相对平均。

找出评价矩阵中评价函数最小的初始作业J*，然后将最佳作业J*与k中的其他候选作业两两配对，生成（k-1）个训练样本，由于生成的（k-1）个训练样本总数通常不足以使模型能够可靠的学习整个新功能，因此在线偏好学习算法维护着一组最近的样本池T，这些新的训练样本已经累积到样本池T中，然后，该样本池T中的所有样本都将学习新的偏好进而更新偏好函数用于下一次作业分配。

2.3 基于改进卷积神经网络的在线学习

候选作业之间的偏好选择可以归于多分类问题，通过改进的卷积神经网络使用增量学习策略对偏好函数进行学习。改进卷积神经网络模型如图2所示，将InceptionNet和传统卷积神经网络相结合，从网络结构和参数优化方面构造了新的分类模型。首先将每个作业两两比较转化成一个15×7的矩阵输入得到第一层，通过三个不同的分支1×3的卷积、1×5的卷积、1×7的卷积进行特征变换得到三个15×16的卷积，随后通过聚合操作将三个分支的结果进行合并得到了最终的过滤器作为下一个卷积层的输入。按照与上一层相同的逻辑，再分别经过三个1×3的卷积、1×5的卷积、1×7的卷积的特征变换，并通过全局平均池化层得到三个8×32的卷积，最后通过维度的聚合在输出通道上将三个分支的结果进行合并输出一个长度为6的向量，因为同时有6个作业进行分类，激活函数采用的是Softmax函数。与传统的卷积神经网络相比，基于InceptionNet的改进卷积神经网络虽然在每层卷积前面增加了三个1×3的卷积、1×5的卷积、1×7的卷积，增加了网络层数，但是去除了最后的全连接层，使用全局平均池化层代替全连接层，进而减少了参数的数量，提高了运算速度并减轻过拟合，同时网络中卷积核的大小也不一样，增加了神经网络对不同尺度的适应性。

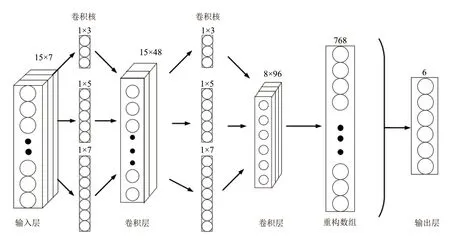
图2 改进卷积神经网络的网络结构

3 实验场景与结果分析

3.1 实验场景

本实验采用Python语言实现，进行实验的计算机参数为Inter（R）Core（TM）i7-7700HQ CPU @ 2.80GHz 2.80GHz，内存16G，Windows10。实验中的自动化集装箱码头布局如图3所示。

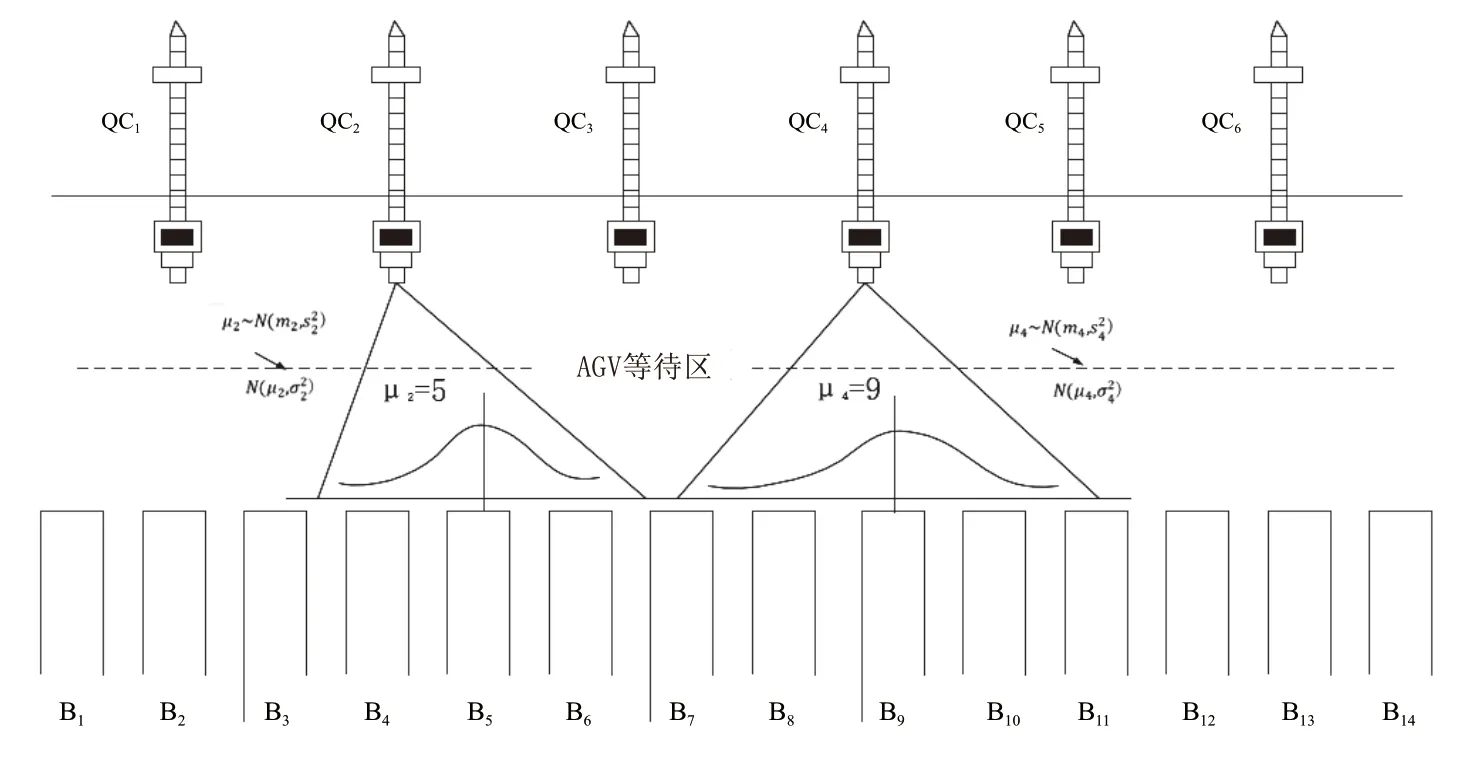
图3 自动化集装箱码头布局

假设有6个QC，集装箱堆场数量为14，总共有900个集装箱作业，实验模拟的AGV数量为12，18，24，速度v=4m/s，ωT:ωD=1:1，QC所处理的集装箱作业目的堆场编号服从正态分布N（μi，σ2i）。如μ4=9时，表示由QC4所处理的集装箱存放在堆场B9附近，随着σ4的增大或减小，集装箱存放在B9的更大或更小范围内，因此可以通过改变μi和σi的值，来模拟不同的实验场景。

设计了两个实验场景，每个实验场景包含900个集装箱作业。场景1设置为各个QC所处理的集装箱大都分布在最近的堆场周围，AGV的负载距离都相对均匀和较短，此时集装箱的分布参数设置为（μ1，μ2，μ3，μ4，μ5，μ6）=（2，4，6，9，11，13），σi=1，场景2设置为集装箱被广泛的分布在各个堆场，AGV的负载距离各不均匀，此时集装箱的分布参数设置为（μ1，μ2，μ3，μ4，μ5，μ6）=（4，5，6，7，8，9），σi=5。

3.2 实验结果分析

3.2.1 实验1结果分析

在场景1的情况下，确定合适的样本池容量上限大小，为后续实验做好基础。

表3显示了通过从样本池中的样本学习来更新偏好功能所花费的CPU时间。学习时间包括生成训练示例和计算所花费的时间。

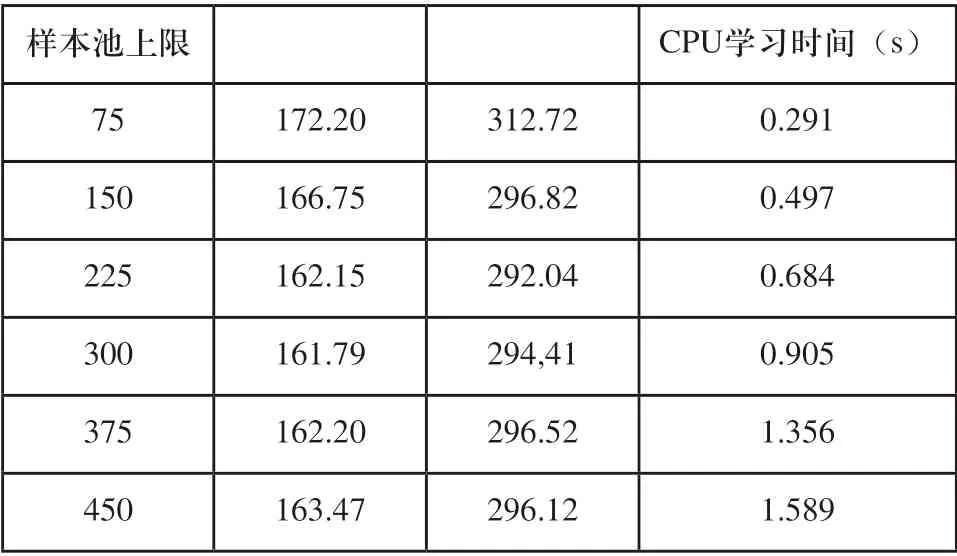
表3 场景1样本容量实验结果

由表3可知，尽管学习时间随样本池上限的增加而增加，但仍为1秒左右，对于在AGV调度中进行实时处理来说足够了。当样本池中数据过多时，随着样本池上限的增加，Tn和Dn都会有所增加，CPU学习时间随着样本池上限的增加而增加，指派算法的性能下降，就会导致模型无法准确获取不断变化的指派规则。当样本池上限R=225时，CPU学习时间为0.684s，小于1s，可以接受，由此后续实验，将样本池上限R设置为225。

3.2.2 实验2结果分析

比较12～24台不同规模的AGV在场景1和场景2下的调度结果。

实验结果如表4所示，当AGV的数量从12逐渐增加到24时，Tn和Dn减少的速率逐步放缓，因为随着AGV的数量的增加，同样也可能会伴随AGV之间的冲突。

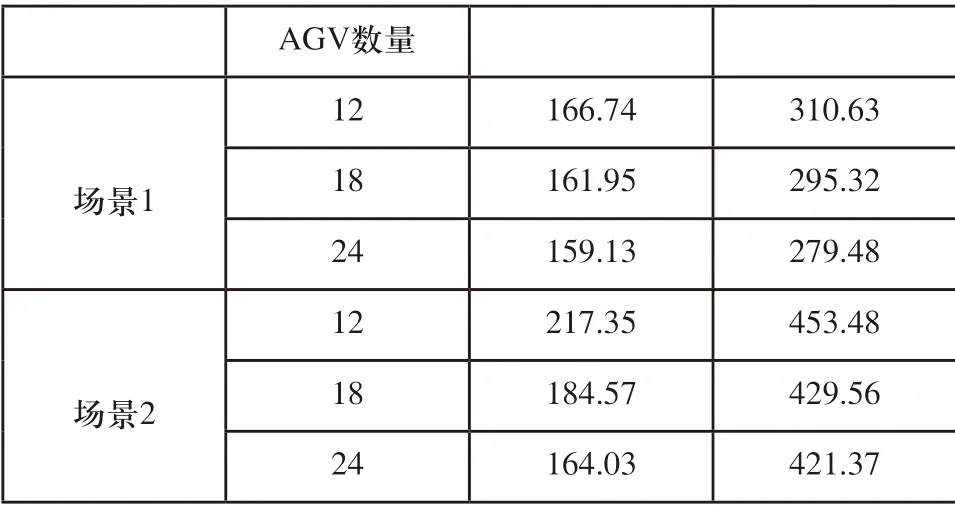
表4 不同场景下AGV的调度情况

1）场景2下的和都高于场景1，这是因为场景2的集装箱散落在各个堆场之间，动态程度更高，AGV的负载距离是不均匀的。

2）当集装箱作业数量相同时，场景1下18台AGV运行下的与场景2下24台AGV运行下的接近。因此可以根据QC和AGV的信息收集和集装箱作业的偏好，对指派策略进行调整，从而减少AGV数量的投入。

3.2.3 实验3结果分析

通过改变集装箱作业的数量，比较采用基于多特征的在线学习指派策略与采用最短车程指派策略的调度结果。

由图4可知，采用多特征在线学习指派策略下比采用最短车程指派策略的Dn大约多了13%，但是随着QC所处理的集装箱数量增加，多特征在线学习指派策略与最短车程指派策略间的Dn差值大约不变。两种指派策略情况下总完成时间随着集装箱数量增加不断增加，采用多特征在线学习指派策略的总完成时间比采用最短车程指派策略的总完成时间约平均缩短12%，当每个QC平均处理约225个TEU时，采用多特征在线学习指派策略能节省约21%总完成时间。

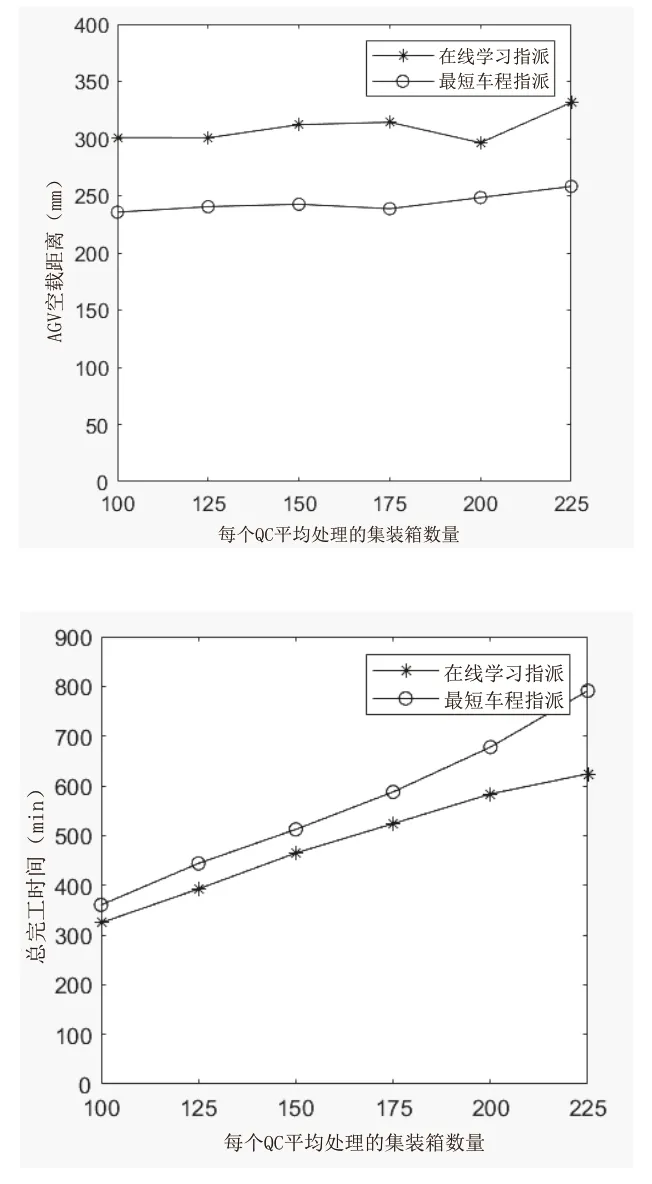
图4 不同指派规则下的调度结果

由表5可知，两种指派策略下的QC的Tn差值为3.9s，26.2s，33.8s，56.4s等，并且随着集装箱数量的增加，在线学习指派策略和最短车程指派策略之间Tn差值不断增加，说明基于多特征的在线学习指派策略能够有效减少QC的平均作业时间和最小化完成时间。

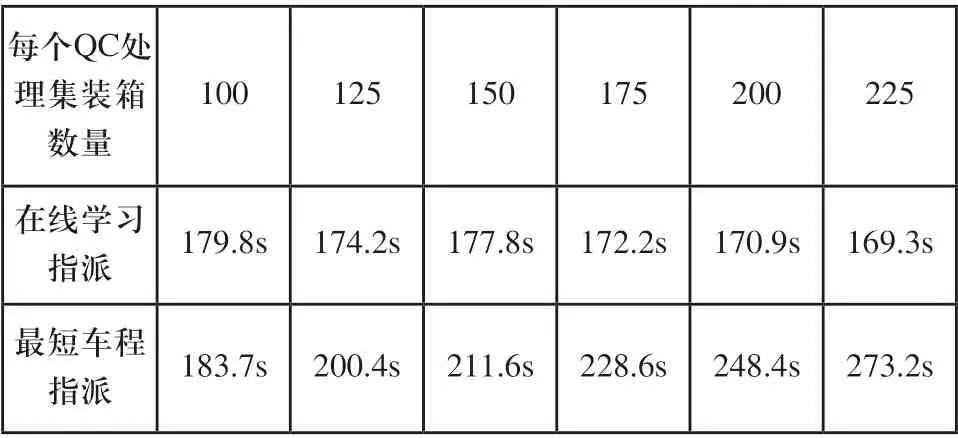
表5 不同指派规则下的QC平均完成时间

4 结语

本文设计了一种基于InceptionNet的卷积神经网络模型，使用全局平均池化层代替了全连接层，减少了参数数量，同时InceptionNet通过分支的方式增大网络的深度和宽度能够很好的提高网络的性能，避免过拟合。然后使用改进的卷积神经网络用于在线学习基于多特征指派策略的AGV动态调度模型，并通过更新偏好函数来进行指派策略的调整。设计了三组实验，首先确定样本池容量实验，R=225，然后进一步对12～24台不同规模的AGV在作业动态程度不同的情况下的调度结果进行分析，表明在场景1的情况下18台AGV的Tn与场景2下24台AGV的Tn十分接近，因此可以根据集装箱作业的分布，减少AGV运行数量。最后对比了基于多特征的在线学习指派策略与最短车程指派策略，实验结果表明，随着集装箱作业量的增加，采用基于多特征的在线学习指派策略比采用最短车程指派策略的Tn约平均缩短17%，总完成时间均大约缩短12%。验证了提出的基于多特征指派策略能够有效的提高AGV作业效率。