基于量子粒子群优化BP网络的计算机层析成像反演算法

刘李楠

（海军士官学校，安徽 蚌埠 233012）

1 引言

计算机层析成像就是利用地震波、电容值或电阻率变化等测量数据来反演地质或物体内部结构的物质属性，并逐层剖析绘制其图像的技术，是目前应用最广泛的工程地质探测和工业成像方法。成像问题的核心最终归结于一个稀疏病态、混定、不相容方程组的求解[1-6]，因此反演算法在整个层析成像技术中处于核心地位，反演算法的优劣将直接关系层析成像的成败。

层析成像中的反演方法可分为线性方法和非线性方法两种。有效的线性反演方法主要有：Van 和Vorst[7]提出了双稳定共轭梯度法（BICGSTAB），它可以用于求解系数矩阵不对称的线性方程组，它利用短递归的方法逐步减小残量，占用内存少，但收敛不规则，在有限精度运算时，这种不规则可能减慢收敛的速度；杨文采[8]提出的带阻尼因子的LSQR 算法（DLSQR），提高了反演计算精度，避免了LSQR 算法在数据误差大时造成的数值不稳定，特别适于求解系数为大型稀疏矩阵的方程组，与其他迭代方法相比，在解奇异或病态问题时，显示出更快的收敛性及更好的可接受的结果，是目前最常用的线性反演方法；此外还有诸如精细积分迭代反演算法等方法，都从某些方面提升了反演计算的性能。非线性反演方法主要有：遗传算法、模拟退火、粒子群和神经网络方法[9]等。

由于层析反演方程组是大型稀疏的非线性方程组，采用线性反演算法求解非线性问题不可避免地带来了解的不适定性等问题，虽然计算速度快但往往精度较低，稳定性也较差。近年来，随着运算平台计算能力的大幅提升，以集群智能寻优算法为代表的智能方法，因其良好的自适应及全局搜索能力在工程技术中有了越来越多的应用，它能更好地排除随机干扰带来的影响，对复杂介质分布重建效果也更为优越。

本文提出了一种利用量子行为粒子群算法（QPSO）优化BP网络解决非线性反演问题的方法，利用QPSO算法中粒子的量子随机性优化BP 神经网络的权值和阈值，提升网络反演计算能力，仿真实验表明了方法的有效性。

2 基本原理

2.1 量子行为粒子群算法

粒子群算法（PSO）是一种群体智能优化算法，通过对预设初始解的迭代运算搜寻最优值，具有易于实现、参数管理少等优点。但从本质上说，其不是一种全局收敛算法，受解空间局限、位置进化公式等影响，算法中粒子的随机性和智能性降低，易陷入局部极值导致鲁棒性降低。孙俊等将量子空间引入PSO算法，利用量子理论中的测不准原理来取代经典力学理论中的粒子运动行为，极大地增强了解空间中粒子的随机性，使得解落入局部极值的概率大大降低，全局搜索能力得到极大增强。

这一过程中，最主要的贡献即为通过引入量子行为优化了粒子位置更新公式[10]：

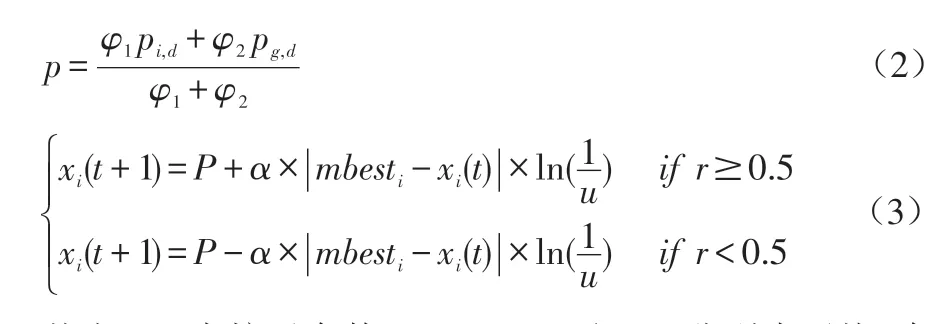
其中，M为粒子个数，mbest、pi,d和pg,d分别为平均、个体和整个群体的迭代当前最优位置；α为扩张参数。

2.2 BP神经网络的基本原理

BP 算法实际上就是含有隐层的多层前馈网络，核心是信息向前传播而误差向后传播，当输出期望值达不到预设输出时，会利用误差反向传播来修改网络的权值和阈值，使得网络结构更加优化。然而单一的BP神经网络方法也有其明显的困难与缺点，如收敛性、局部极小以及隐层神经元个数的选取等。本质上BP 神经网络方法是随机的，依赖于空间误差表面的瞬时梯度值，因此收敛速度可能较慢甚至可能不收敛，易陷入局部极小，时间开销较大，因此在应用时可以综合运用其他方法来优化，提升网络的收敛性和准确性。

3 基于QPSO优化BP网络反演算法

QPSO算法优化BP网络反演计算分为两部分，如图1所示，主体右侧是BP网络训练部分，左侧是QPSO算法优化部分。QPSO算法中粒子代表BP网络中的权值和阈值，利用每个粒子表示候选解空间内的一个解，解的优劣由适应度函数衡量，这个适应度函数是根据具体的优化目标而选取。如本文计算机层析成像反演计算中，粒子代表了BP 网络的权值和阈值，适应度函数可选为BP 网络计算权值阈值与期望权值阈值的预测误差，适应度函数的优化就是寻求误差最小的过程。左右部分往返调用，迭代寻找最优的粒子，即为BP网络权值和阈值的最优设置，建立了基于QPSO 优化的BP 网络反演算法（QPSO-BP反演算法）。

图1 QPSO优化BP网络反演算法流程图

采用QPSO-BP 算法进行计算机层析成像反演计算，具体步骤及参数选择如下：

（1）初始化：采用三层网络结构，输入层为监测点测量数据，节点数选择为10；输出层为反演介质网格分布，节点数为10；隐层节点数根据经验选择为21。得出权值为420 个，阈值为41个。

（2）计算适应度函数值：选择BP网络训练实际输出值和期望输出值的差来计算适应度函数值。

（3）集群更新：如果适应度不满足，按QPSO 算法更新，重复计算；如果满足即停止，输出最优权值和阈值，完成网络训练及优化。

（4）反演计算：完成网络训练后，将新测量炮点走时或电阻率数据输入训练好的BP网络，经计算得到最终反演结果，完成不同介质计算机层析成像图形重建。

4 仿真结果与分析

为了验证反演算法的效果，建立二维层状介质模型，见图2，模型尺寸均为100×300m，层状介质速度模型在0～150m深度范围内有5 层，每层厚度均为30m；150～300m 深度范围内有3 层，每层厚度均为50 米；从顶层至底层速度值分别为1800m/s、2000m/s、2200m/s、2400m/s、2600m/s、2800m/s、3000m/s及3200m/s。采用“井间”观测方式，地表左侧井位置坐标为（0,0），发射源置于左侧井中，个数为10 个，第一个发射点位于深度10m处，均匀分布，间距为20m，接收点位于右侧井，地表右侧井位置坐标为（100,0），接收点数目及深度分布同发射点。

图2 二维层状介质模型图

采用相同的离散规则网格，利用不同的反演方法求解计算。根据发射点至接收点射线建立反演方程，此时反演计算属于超定问题无法得到精确解，分别采用PSO-BP 和QPSOBP 算法进行求解。参数设置中，PSO 算法中粒子种群规模设置为80，QPSO 算法中粒子种群规模为20，最大迭代次数均为400，粒子速度取值区间为[-1，1]，扩张参数α为0.7；BP网络部分，最大迭代代数设置为100，不设置训练终止条件。采用MATLAB 7.0，在硬件Intel（R）Core（TM）i5-3230M CPU 2.6G Hz，8G内存的机器上运行，适应度进化曲线、反演计算相对误差如图3、4所示。

图3 两种算法适应度进化曲线图

图4 两种算法反演重建结果相对误差图

从图3中可以看出，两种算法都完成了测量数据的反演重建工作。QPSO算法由于对粒子位置更新采用量子行为极大增强了粒子运动的随机性，迅速提升了全局寻优能力，在适应度计算迭代到约50次时已经基本到达了最优，具有很好的快速寻优能力。从误差图中看出，除个别网格介质分布误差较大外，大部分相对误差在0.03 以内，基本完成了分层检测板重建工作，PSO-BP 算法的最大误差为0.097，最小误差为9.73e-005，平均误差为0.0218；而QPSO-BP算法计算最大误差为0.065，最小误差为1.49e-004，平均误差为0.0098。仿真结果表明，QPSO-BP算法反演结果能更准确反映出模型中各层速度分布，具有很好的反演效果。

5 结论

层析成像的核心是反演计算，反演计算的重点即是对大型、病态方程组的求解，本文将量子行为粒子群算法引入BP神经网络权值和阈值优化，然后利用优化训练后的网络进行反演计算，主要具有以下优点：

（1）计算效率高。适应度值能快速收敛最优，通过适应度进化曲线图可以看出经过不到50次寻优，适应度基本达到了最优，收敛速度几乎是PSO方法的三分之一。

（2）应用性强。仿真实验中，PSO 方法粒子种群数目为80，而QPSO 方法粒子种群数目为20 时即能更好完成任务，计算过程中参数选取以及迭代条件不会显著影响收敛性、收敛速度，具有较好的应用前景。