基于Fluent的涡轮流量计前导流体改进研究∗

冯 越任建强王彦华

(廊坊师范学院电子信息工程学院，河北 廊坊 065000)

涡轮流量计是一种速度式流量计，近年来已在石油、化工、科研、国防、计量等领域获得广泛应用[1]。石油、低温液体、有机液体、液化气、天然气等采集、输运、测量各过程的复杂条件决定了应用的流量计必须具有重复性好、量程范围宽、精度高等优点，而涡轮流量计就兼具以上特性[2]。此外，压力损失也是选用涡轮流量计的关键指标，具有较小压力损失的涡轮流量计可减少输运流体的能量消耗，进而节约能源，降低输送成本[3]。

为提高涡轮流量计的计量性能，降低压损，国内外专家学者进行了大量研究工作。Zijad D[4]研究了过渡流中涡轮流量计的测量误差，其研究表明涡轮流量计在加速流中具有良好的动态响应，在减速流中响应速度较慢。Al-Manie M A[5]将进化周期图应用于在线涡轮流量计的状态信号监测，比较并分析了正常涡轮与叶片尖端剪短后涡轮的时频分布。东北大学的顾亚飞[6]设计了一种带有特殊前导叶的改进涡轮流量计，结合理论分析与模拟验证，得出前导叶螺旋角与涡轮螺旋角之和等于90°时，涡轮启动容积流量最小，流量计灵敏度最大的结论。西北工业大学的杜玉环[7]设计了一种双圈同轴式光纤涡轮流量传感器并研究了其流量测量的工作原理及测量优势。中国科学技术大学的王鲁海[8]采用理论和校验实验相结合的方法，分析了小口径涡轮流量计在复杂条件下的响应情况。

前人对涡轮流量计的改进研究主要基于测量原理和测量方法的更新，而对现有结构的改进优化相对较少。本文通过对涡轮流量计工作原理、结构组成的分析，选取其重要组成部件前导流体进行改进。基于流体仿真软件Fluent的数值模拟，获得了不同前导流体结构下的流场速度分布情况和均匀性指标，据此提出了改进方案，再结合实流实验比较不同结构参数下涡轮流量计的计量指标数据，最终验证了改进方案的优越性。

1 涡轮流量计工作原理与结构组成

1.1 工作原理

涡轮流量计是一种速度式叶轮流量测量仪表，它利用置于流体中的叶轮的旋转角速度与流体流速的正比关系，通过测量叶轮旋转的频率得到流体流速，进而得到管道内的流量值[9]。

不考虑叶轮上所受的摩擦阻力矩和流体阻力矩的理想工作状态下，流量方程[10]如下所示:

式中:qv为体积流量，f为叶轮旋转频率，r为半径，A为流通截面积，β为叶片安装角，N为叶片个数。

旋转频率f由流体平均流速¯v所决定:

由式(3)可知，叶轮的旋转角速度和流体进入叶轮的平均速度成正比关系，进而与流体体积流量成正比。所以进入叶轮前的速度分布直接影响涡轮流量计的计量稳定性[11]，研究进入叶轮前的速度分布可为涡轮流量计的改进提供思路。

1.2 结构组成

涡轮流量计结构示意图如图1所示，主要部件包括前导流体、叶轮、后导流体。前导流体具有收敛和导向两个重要作用，可保证涡轮流量计的准确度[3]。此外，当现场安装不能提供足够长的前直管段时，可通过前导流体调整来流流场达到测量要求。综上，前导流体具有整流作用，直接影响流体进入叶轮前的速度分布。

图1 涡轮流量计结构示意图

由前面的理论分析可知，进入叶轮前的速度分布关系着流量计的计量稳定性。所以，前导流体的结构改进对于提高涡轮流量计性能具有重要意义。

2 基于Fluent的改进设计方法

2.1 前处理过程

本文重点考察前导流体的整流作用，而涡轮叶片位于前导流体后端，对前导流体的整流效果没有直接影响[12]。此外，加入涡轮叶片会消耗大量计算资源。所以为了提高计算效率，在前处理阶段，仿真建模时未考虑涡轮叶片。

首先通过Gambit建立三维几何模型，如图2所示。圆管口径D为50 mm，长度L为500 mm，前导流体叶片8片，后导流体叶片3片。进行网格无关性验证，网格数为30万左右(因结构不同，网格总数略有变化)。规则结构处采用六面体类型的结构化网格，非规则处采用四面体类型的非结构化网格，同时在前导流体周围进行网格加密，网格划分如图3所示。Fluent求解器的边界条件设置如下:入口设置为速度入口，具体数值根据流量值计算；出口设置为压力出口，设为一个大气压。壁面条件为0.5 mm粗糙度，无传热传质。

图2 三维几何模型

图3 网格划分

2.2 计算模型的选择和验证

湍流运动复杂难寻，因此选择一个合适的湍流模型尤为重要[13]。结合实际流动工况及雷诺数等指标，选用k-ε-standard模型。该模型计算量适中，应用广泛，有较多的数据积累和较高的计算精度[14]，满足本文数值模拟的需求。通过比较k-ωstandard，k-ε-RNG，k-ε-standard三种常用湍流模型下，流体流经前导流体后速度分布和误差大小，验证该模型的可行性。

图4中(a)、(b)、(c)分别对应k-ω-standard、kε-RNG、k-ε-standard三种模型下叶轮处径向截面的速度分布云图。对比观察，仅有k-ε-standard模型下，叶轮处的速度云图呈中心对称分布。由于前导流体的几何模型是8片叶片的中心对称结构，所以实际流场的速度也应呈中心对称分布。可见k-εstandard模型的仿真结果最能反映真实流场。

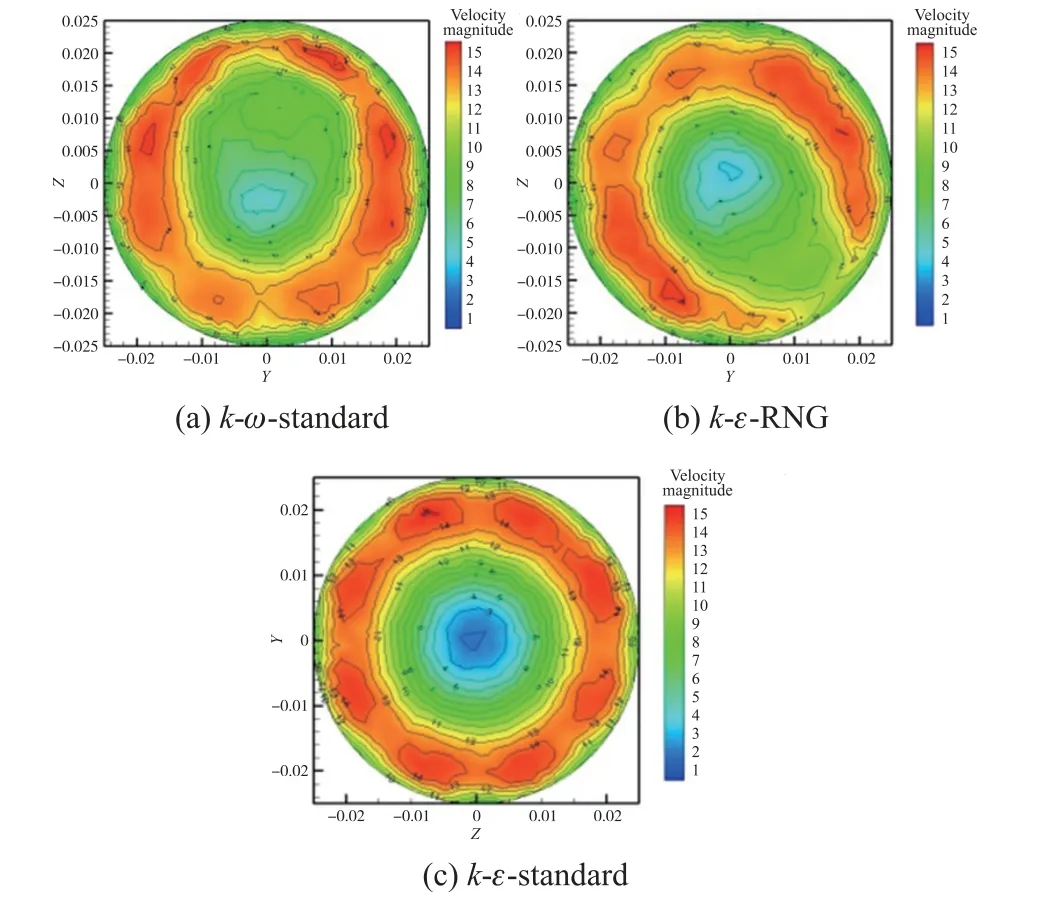
图4 叶轮处速度分布云图

选用k-ε-standard模型后，比较了不同流量点下仿真速度与理论速度之间的相对误差，结果如下表1所示。体积流量分别为7.85 m3/h、43.17 m3/h以及78.50 m3/h时，仿真速度的相对误差均在1%以内。

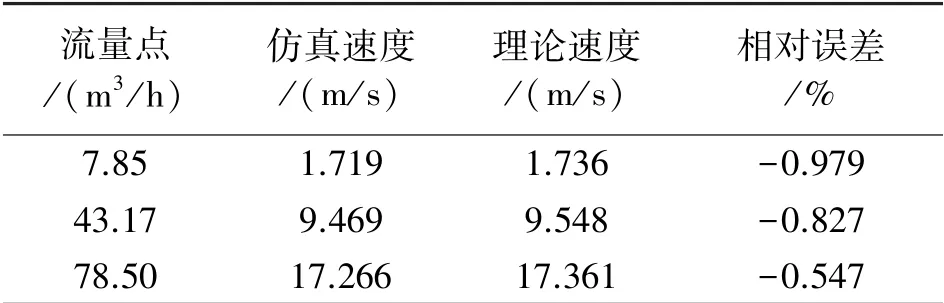
表1 不同流量点下的仿真速度与理论速度比较

综上，选择k-ε-standard模型作为湍流模型具有可行性，其仿真流场真实可靠，仿真结果满足本研究数值模拟的误差需求。

2.3 考察指标选择

流体的流动均匀性在很多研究领域中都是很重要的衡量指标[15]。均匀性指数γ[16]描述了指定表面上指定物理量的变化情况，取值范围为[0，1]，取值越大表示均匀性越好。均匀性指数可以采用面积或质量进行衡量:area-weighted均匀性指数捕捉量的变化(如组分浓度)，mass-weighted均匀性指数捕捉通量的变化(如组分通量)。

指定场变量ϕ的area-weighted均匀性指数γα，利用下式进行计算:

式中:Ai表示第i个单元面积矢量，ϕ为指定场变量，ϕi为对应Ai的场变量，¯ϕα为整个表面的面积加权平均值，按下式计算所得:

从定义可以看出，均匀性指数可以描述流场均匀性。前导流体的作用就是使来流的流速均匀，实现流场均匀稳定的整流效果，所以均匀性指数可以作为改进效果的一个考察指标。当指定场变量为速度v时，γα表示流场速度分布均匀性，并且γα可由Fluent软件提供，为数值模拟的后处理工作提供方便。综上，选用γα作为流场分析的考察指标。

3 前导流体作用下流场分析

选取前导流体直径、前导流体与轮毂间距离作为改进参数，对不同前导流体结构参数下的流场进行仿真分析，对比其整流效果优劣。

3.1 弯管对速度分布的影响

为了模拟实际流动中的不稳定流场，考察前导流体的整流效果，引入弯管的设计，在前导流体前设置90°弯管，三维几何模型如图5所示。

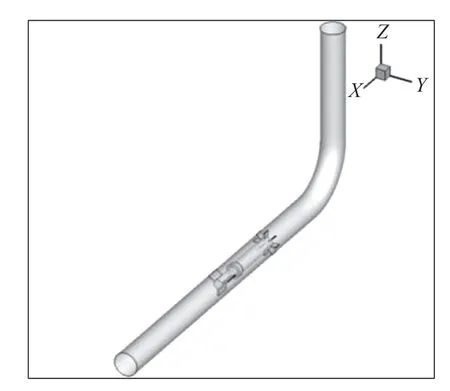
图5 带有弯管的几何模型

弯管距前导流体的距离分别设置为1D、2D、3D、5D、10D，为了监测弯管造成的不稳定来流，分别取前导流体前1D处的速度分布云图，如图6所示。

由图6(a)～(e)与(f)有无弯管的速度分布云图对比看出，弯管对流场有较大的影响。弯管距离前导流体越近，前导流体之前的流场越紊乱，表现为速度分布云图上的速度等值线不均匀变化，沿径向呈非对称分布。随着弯管与前导流体间距离增大，对流场的影响逐渐减小，导流体前的流场趋于稳定，但仍表现出速度沿径向不对称分布特点。

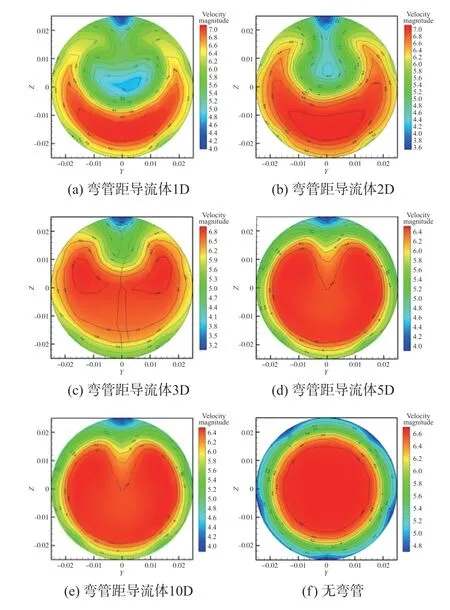
图6 前导流体前1D处的径向截面速度分布云图

为了考察前导流体的整流效果，监测流体流经前导流体后在叶轮处的均匀性指标，如图7所示。从图中可以看出，随着弯管距前导流体的距离增大，速度分布的γα指数逐渐变大，表明速度场的均匀性逐渐变好；当距离大于5D后，γα指数的变化趋于平缓，表明弯管造成的流场紊乱可基本消除。

图7 不同距离下叶轮处的均匀性指数

3.2 前导流体不同直径

在轮毂的直径确定的情况下，分别取比轮毂直径小5 mm(－5 mm)、与轮毂直径相同(0 mm)以及比轮毂直径大5 mm(＋5 mm)数值作为前导流体的直径进行仿真实验，叶轮处速度分布图和均匀性指标，如图8、图9所示。

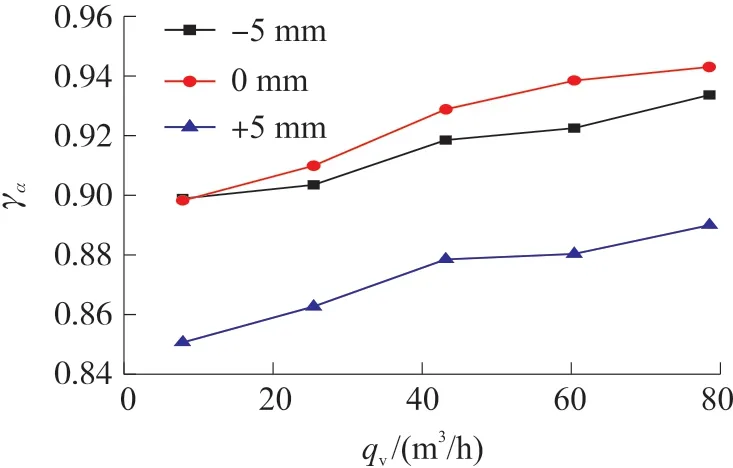
图9 不同前导流体直径下的均匀性指数

由图8可以看出，在导流体直径与轮毂直径相同时，叶轮处径向截面的速度场梯度最小，即速度分布最为平稳；导流体直径比轮毂直径大5 mm时，速度场梯度最大，速度分布最紊乱。

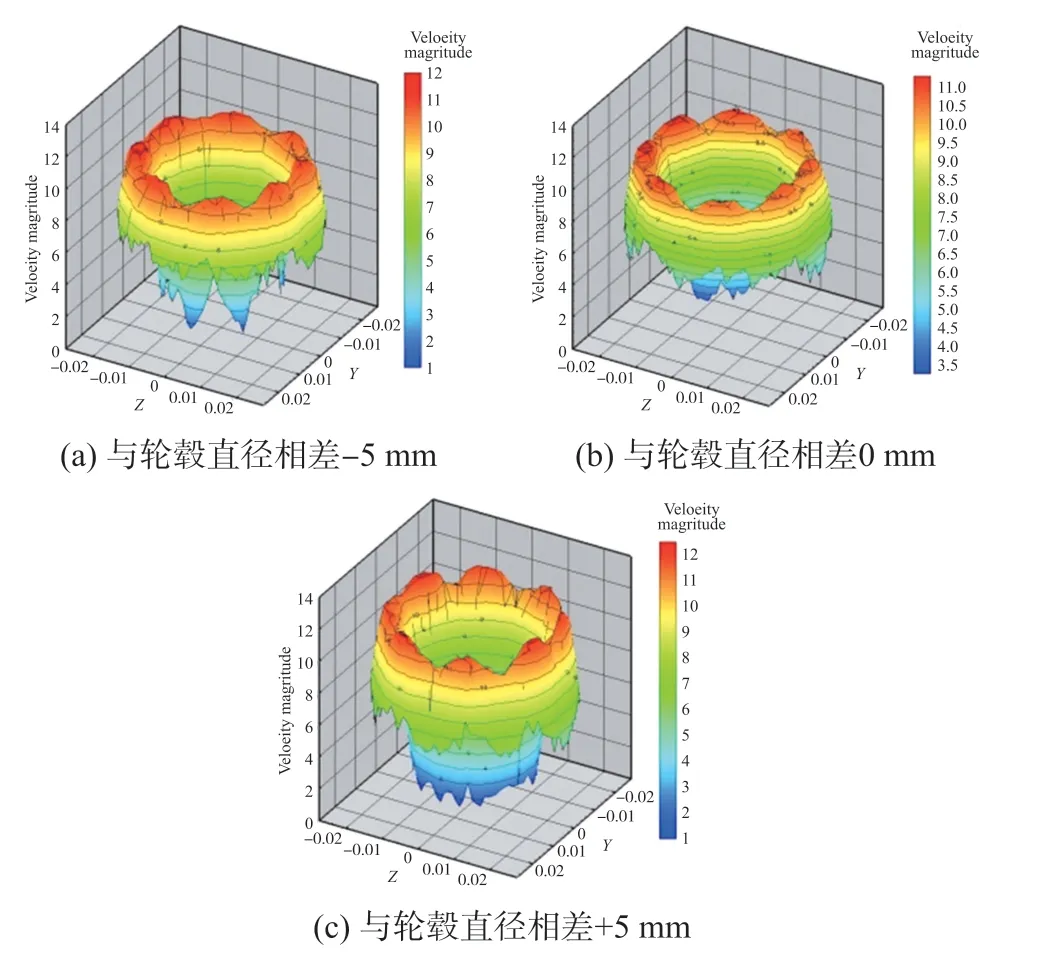
图8 不同导流体直径下速度分布三维立体图

由图9可以看出，随着流量增加，叶轮处的γα指数增大，流场的速度均匀性变好。在导流体直径与轮毂直径相同时，叶轮处的γα指数在各流量点下都最大，即速度均匀性最好；导流体直径比轮毂直径大5 mm时，γα指数在各流量点下都最小，即速度均匀性最差。综上，当前导流体直径与轮毂直径相同时，整流效果最优，推荐采用。

3.3 前导流体与轮毂不同距离

为研究前导流体与轮毂间距离变化对整流效果的影响，分别建立前导流体与轮毂距离为3 mm、5 mm、10 mm三种几何模型，再进行数值模拟，得到叶轮处速度分布和均匀性指标，如图10、图11。

图10 叶轮处速度分布三维立体图

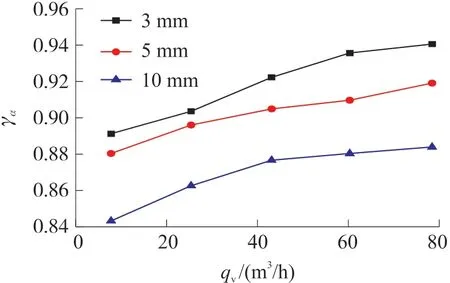
图11 叶轮处均匀性指标

由图10可以看出，在导流体距轮毂3 mm时，叶轮处径向截面的速度场梯度最小，即速度分布最为平稳；随着导流体与轮毂间距离变大，速度梯度也随之变大，速度场逐渐紊乱。由图11可以看出，导流体距轮毂3 mm时，叶轮处的γα指数在各流量点下都最大，即速度均匀性最好；导流体距轮毂10 mm时，γα指数在各流量点下都最小，即速度均匀性最差。推测可能的原因是随着距离增大，前导流体的整流作用逐渐减弱，使得速度场的均匀性变差。综上，当导流体距离轮毂越近时，整流效果越好，建议在保证安装条件的情况下，两者的距离越小越好。

4 实验验证

在天津大学音速喷嘴气体流量标准装置[17]上进行实验，验证上述改进思路的有效性。依据涡轮流量计的检定规程[18]，比较不同前导流体结构下涡轮流量计的计量性能指标:仪表系数、重复性误差、线性度误差、压力损失。

4.1 扰流测试验证

通过不同的前直管段条件(1D、3D、5D、90°弯管、阀门)的组合，对现有涡轮流量计进行实流标定测试，测试其对于不同前直管段的适应性，实验结果如表2所示。

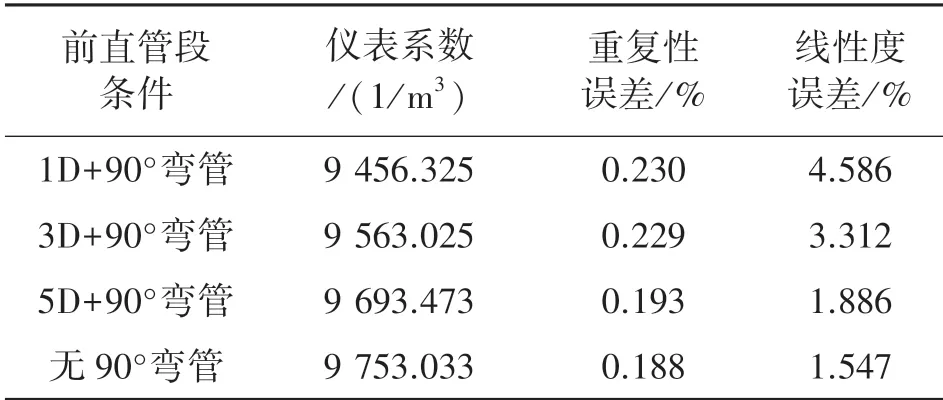
表2 不同直管段条件下的计量性能指标

由上表看出，有弯管情况下前直管段长度达到5D时，仪表系数最大，表征单位体积的流体流过流量计时发出的脉冲数最多；重复性误差最小，在0.2%以内；线性度误差最小，在2%以内，此时涡轮流量计的各项计量指标最接近无弯管时的数据，可以认为弯管与涡轮流量计距离大于5D后，弯管造成的干扰可基本消除，与上述仿真结果结论一致。

4.2 前导流体不同直径验证

在现有叶轮轮毂直径30 mm的基础上，分别加工前导流体直径比轮毂直径小5 mm、与轮毂直径相同以及比轮毂直径大5 mm三种机芯直径，再测试三种结构下的涡轮流量计的计量性能指标，实验结果如表3所示。

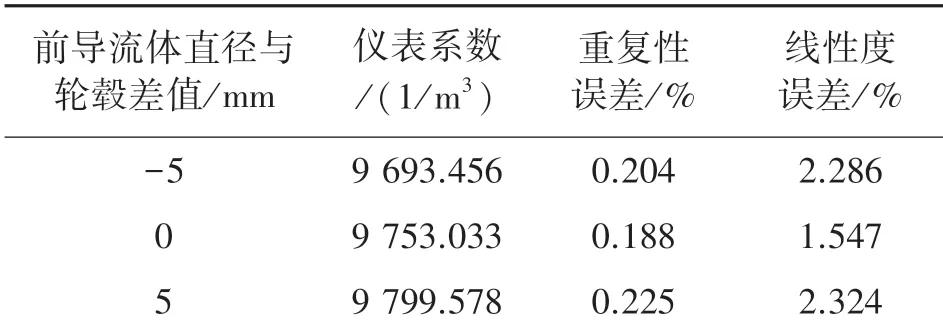
表3 不同前导流体直径下的计量性能指标

从表3可以看出，当前导流体直径与叶轮轮毂直径相同时，其重复性误差、线性误差最小。使用U型管压力计进行压损测试，即在不同前导流体直径条件下测量流量传感器上下游的压力差值。实验结果如图12所示。

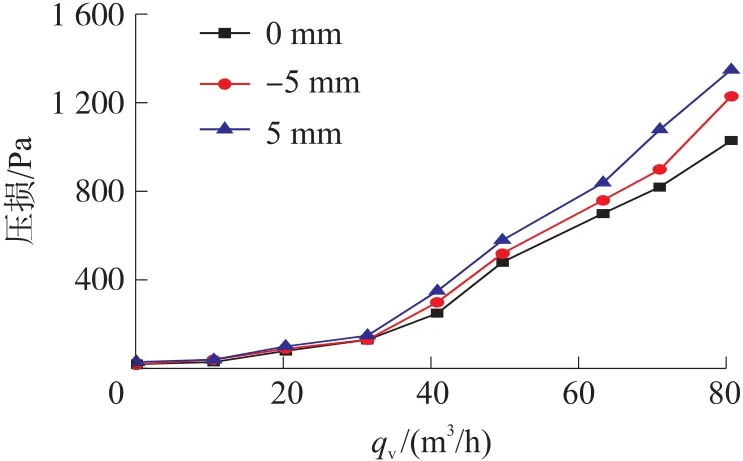
图12 不同前导流体直径下的压损

从图12可以看出，压损会随着流量值的增大而增大。在各流量点下，压损最小的情况均出现在前导流体与轮毂直径相同时。在最大测试流量点80.58 m3/h时，相同直径的比直径差值为＋5 mm的压损减少23.7%。因为相同的直径可以避免流体因流通面积的变化而导致的能量损耗。

4.3 前导流体与轮毂间不同距离验证

实流测试时，前导流体与轮毂间距离受现场安装条件的限制，设置为15 mm，25 mm，50 mm，为数值模拟时的等比例放大。测试三种距离下涡轮流量计的计量性能指标，实验结果表4如所示。

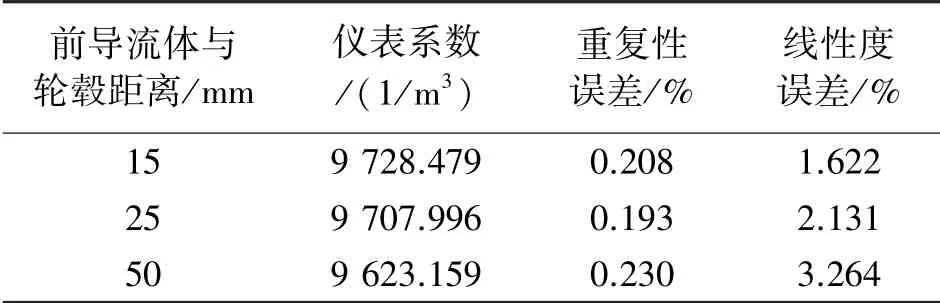
表4 不同前导流体与轮毂间距下的计量性能指标

从表4可以看出，前导流体与轮毂距离15 mm时，线性误差最小，在2%以内，但重复性误差并没有明显优势。进行压损测试，实验结果如图13所示。压损会随着流量值的增大而增大，但在各流量点下，压损最小的情况均出现在前导流体与轮毂距离15 mm时，即两者间距最短时。在最大测试流量点80.58 m3/h时，间距最短的比间距最大的压损减少28.9%。推测可能的原因是前导流体与轮毂距离越小，中间的空程距离越短，流动一致性越好，能量损耗越小。

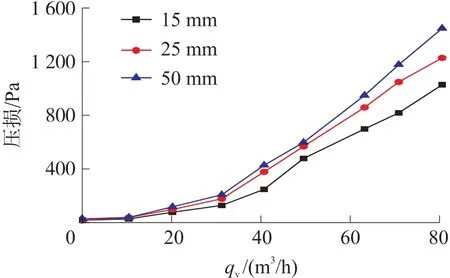
图13 不同前导流体与轮毂距离下的压损

5 总结

本文通过对涡轮流量计工作原理、结构组成的分析，基于Fluent仿真提出对前导流体的改进方法，并通过实验手段加以验证，得到以下结论:①数值模拟方法在一定程度上可反映涡轮流量计内部流场信息，为涡轮流量计的结构改进提供辅助手段，流场均匀性指标可有效评价整流效果。②在有弯管干扰时，导流体前预留5D的距离可以基本消除干扰，可以达到测量要求。③前导流体的直径与轮毂直径一致的改进设计可行，可得到较好的计量性能指标和较低的压力损耗，最大流量80.58m3/h时，压损减少23.7%。④前导流体与轮毂距离尽可能接近的改进设计可行，可得到较好的线性度指标和较低的压力损耗，最大流量80.58 m3/h时，压损减少28.9%。