基于空气流体力学原理解析火力发电厂空冷塔布置

塔拉，额尔敦毕力格，白 阳，樊洛岑，刘诗媛

(1. 内蒙古电力勘测设计院有限责任公司，内蒙古 呼和浩特 010010；2. 内蒙古中实工程招标咨询有限责任公司，内蒙古 呼和浩特 010010)

0 引 言

火力发电厂汽轮机排汽的空气冷却设施分为直接空冷塔和间接空冷塔。直接空冷塔也叫空冷岛；间接空冷塔又分为自然通风间冷塔和机械通风间冷塔，但大中型火力发电厂一般采用自然通风间冷塔。本文中主要对空冷岛和自然通风间冷塔布置进行分析研究。对于空冷岛和自然通风间冷塔布置来说，最受关注的分别为炉后来风和塔群通道效应问题。对于炉后来风和塔群通道效应问题，行业内从各种角度上进行过较深的研究，但从空气流体力学原理上对其进行分析的较少。炉后来风和塔群通道效应问题，本质上是空气气流遇到障碍物产生的效果。

基于此，本文从解释空气气流遇到障碍物产生的效应入手，并利用其原理解析空冷塔布置典型问题，总结空冷塔布置原因导致的通风效率和气流干扰注意事项。

1 障碍物对空气气流的影响

空气气流遇到障碍物后其方向、密度、速度发生变化，并在障碍物背风面产生复杂的湍流现象。如图1、图2 所示，当大气流过障碍物时，因受到阻碍，在障碍物迎风面下部，风速减弱并且有上升气流(遇到直立的障碍物时，其迎风面由于气流的撞击作用而使静压高于大气压，其风向与来风风向相反，伴随湍流涡动)；障碍物顶部，因为气流流线加密而风速加强；而在障碍物背风面，因气流流线辅散，风速急剧减弱并且有下沉气流，由于重力和惯性作用，背风面气流往往成波状流动，称为尾流扰动区[1]。尾流扰动区风速会降低，还会产生很强的湍流，且该区域空气循环流动与周围大气仅有少量交换。在孤立的障碍物两侧气流，与顶部受到相同的影响，同样风速加强。

图1 气流越过山丘典型矢量图

图2 气流越过直立障碍物典型矢量图

空气气流遇到障碍物后发生的风速变化可以利用风功率公式解释。风功率等于面积、风速的立方、空气密度的乘积[1]，即

式中：W为风功率，W；A为面积，m2；υ为风速，m/s；ρ为空气密度，kg/m3。

理想状态下，对于一个地点来说，空气密度为常数；同时一定宽度和高度范围内，障碍物前后风功率相等。因此障碍物迎风面方向和所处位置上的气流通过面积和速度成反比。障碍物迎风面方向上的气流通过面积大于障碍物所处位置的气流通过面积，因此障碍物顶部和两侧(孤立的障碍物)风速高于其迎风面。而障碍物背风面，从障碍物顶部和两侧流过的外侧气流基本不受影响继续往后流过，而内侧气流受到障碍物背风面空旷区影响：一方面，因背风面空旷区影响，面积增大而速度下降；另一方面，由于重力和惯性作用，气流波状流动，从而产生很强的湍流。所谓湍流是指风速、风向及其垂直分量的迅速扰动或不规律性。另外，受到外侧气流的保护，该区域空气循环流动而与周围大气仅有少量交换。

在障碍物背风面对风速影响的水平距离大致是与障碍物高度和障碍物平均坡度半角的余切的乘积成比例[1]，即

式中：L为障碍物背风面对风速影响的水平距离，m；h为障碍物高度，m；α为障碍物平均坡度角，(°)。

障碍物对空气气流的影响延续至山群时会发生峡谷效应。比如两座山体连线垂直于风向时，即风向与山谷走向一致时，山谷中的风速得到很大的增强。原因是气流受到单个山体阻碍后，山体两侧风速加强，两座山头之间的山谷中两侧的速度本已加强的风力继续叠加在一块，成为强度更大的风力，形成峡谷效应。

2 空冷岛炉后来风问题解析

空冷岛布置中，与气流相互作用关系中最受关注的问题为炉后来风影响。DL/T 5032—2018《火力发电厂总图运输设计规范》5.2.12-1中规定[2]：“宜平行布置在汽机房A 排外侧，空冷凝气器主进风侧宜面向夏季主导风向，并兼顾全年主导风向，避免来自锅炉后及侧后的夏季较高风频和风向；当夏季主导风向与次主导风向形成180°左右对角的厂址，汽机房与空冷岛宜平行主导风向布置。”

锅炉后及侧后的夏季较高风频和风向影响，可利用障碍物对空气气流的影响原理进行解释。可把锅炉房和汽机房看作高大的、孤立的障碍物，炉后来风被锅炉房和汽机房阻碍，风速减弱并且气流上升；在锅炉房和汽机房顶部及两侧风速加强且同时受到锅炉房热量影响，温度进一步升高；在空冷岛区域正好形成尾流扰动区，导致热风集聚，并形成空气循环流动且与周围大气仅有少量交换的封闭区域，进而影响直接空冷系统冷却效率，而且其产生的湍流直接影响空冷岛结构及设备安全。

3 自然通风间冷塔塔群通道效应问题解析

自然通风间冷塔布置中，与气流相互作用关系中最受关注的问题为塔群通道效应。DL/T 5032—2018《火力发电厂总图运输设计规范》5.2.11-2 中规定：“多座自然通风冷却塔(本文中只针对自然通风间冷塔)集中布置时，不宜采用梅花形、菱形、三角形布置形式。”[2]并在5.2.11 条条文说明[2]：“当多座自然通风间冷塔集中群组布置采用梅花形、菱形、三角形布置形式时，容易产生通道效应，即当塔群受到较大的风荷载作用时，后排塔的迎风面产生较大的集中力，发生弹性破坏，而前排塔的背风面会因较大的负压产生弹性稳定破坏。”

所谓的通道效应，实际原理与大气候动力学中的峡谷效应相同。在三角形布置的三座自然通风间冷塔的任何两个塔连线垂直于风向时，气流受到此两座塔阻碍后，冷却塔两侧风速加强，两座塔间区域中两侧的速度本已加强的风力继续叠加在一块，成为强度更大的风力，形成峡谷效应，后面对角线上冷却塔受到峡谷效应会产生集中应力，同时前排塔的背风面产生复杂的湍流和负压。梅花形、菱形布置为三角形布置的延伸，情况变得更加复杂，而且自然通风间冷塔梅花形、菱形布置时基本上都受到任何风向的峡谷效应影响。

从峡谷效应的原理分析，当厂址所在地两个对角方向均存在非常明显的强风，而其他方向风频风能均非常弱时，自然通风间冷塔可以尝试三角形布置，不过其中两座塔的连线需平行于最强对角方向风力、垂直于最弱风力风向，如图3 所示。图中D为自然通风间冷塔常规避开距离。

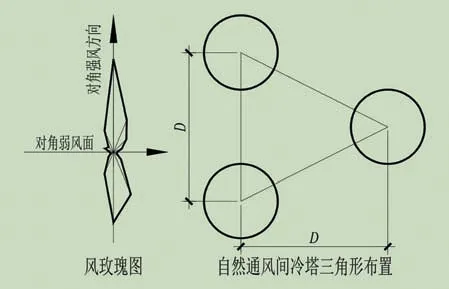
图3 自然通风间冷塔可采用三角形布置情形

另外，“多座自然通风冷却塔集中布置时，不宜采用梅花形、菱形、三角形布置形式”是个相对概念，其基于最佳布置方式和节省结构投资理论。当实际条件不可避免的话，通过冷却塔的工艺优化和结构加强等方式能消除其布置形式带来的不利影响时，也可以采用梅花形、菱形、三角形布置形式，但其结构投资肯定会上升。

4 空冷塔与建(构)筑物方位和间距

确定空冷塔与建(构)筑物之间相对位置时，主要把通风和气流动力干扰作为首要考虑因素。根据障碍物对空气气流的影响原理，厂区较高大建(构)筑物同样会引起空冷岛炉后来风和自然通风间冷塔群通道效应问题。因此，需要利用空气流体力学原理分析建(构)筑物与空冷塔之间的相互作用，合理确定空冷塔与建(构)筑物之间相对位置。确定其相对位置关系后采取合理的间距，降低气流动力干扰影响。国内空冷塔与建(构)筑物的相互通风干扰研究一般都基于湿式冷却塔的研究成果，即

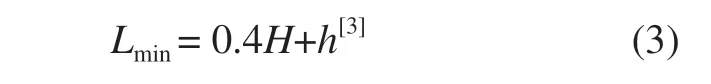
式中：Lmin为空冷塔与建(构)筑物之间最小避让距离，m；H为空冷塔有效进风高度，m；h为建(构)筑物高度，m。

式(3)的原理如图4 所示：首先把冷却塔有效进风面看作为以冷却塔进风高度H为半径的扇形面。其次直立建(构)筑物坡度角可看作90°，那么根据式(2)，直立建(构)筑物影响气流的尾流扰动区水平距离等于建(构)筑物高度，即图中45°三角区为建(构)筑物影响气流的尾流扰动区。那么以冷却塔进风高度H为半径的扇形面与建(构)筑物高度h为短边的45°三角区面不交叉时，可以认为间冷塔与建(构)筑物之间避免了基本的气流影响。根据几何原理，直立建(构)筑物影响气流的尾流扰动区水平距离等于其高度h；以冷却塔进风高度H为半径的扇形面与直立建(构)筑物影响气流的尾流扰动区的45°斜线的切线夹角为45°，而扇形面半径延伸线连接至45°斜线与地面交叉点时正好形成22.5°夹角，tan22.5°=0.414 214。所以间冷塔与建(构)筑物之间最小避让距离为Lmin=0.414 214H+h，简化为Lmin=0.4H+h。通过上述分析，式(3)符合空气流体力学原理。

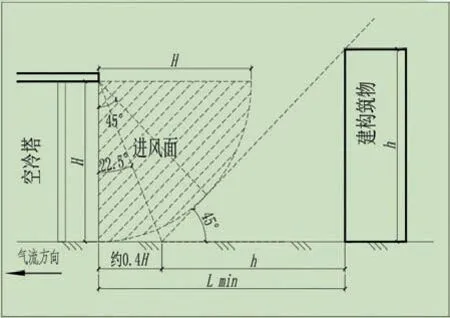
图4 直立建(构)筑物与空冷塔之间最小避让距离

当建(构)筑物为非直立的圆弧形状时，式(3)中的h应等于式(2)中的L，即

式中：Lmin为间冷塔与圆弧形建(构)筑物之间最小避让距离，m；H为间冷塔有效进风高度，m；H为圆弧形建(构)筑物高度，m；α为圆弧形建(构)筑物间冷塔一侧的平均坡度角值，(°)。

也可以利用图5 所示几何原理确定空冷塔与圆弧形建(构)筑物之间最小避让距离。利用式(4)计算的结果与图5 所示几何原理得出得结果是相近的，工程上均可利用，这进一步证明了利用空气流体力学推导空冷塔布置原理的正确性。

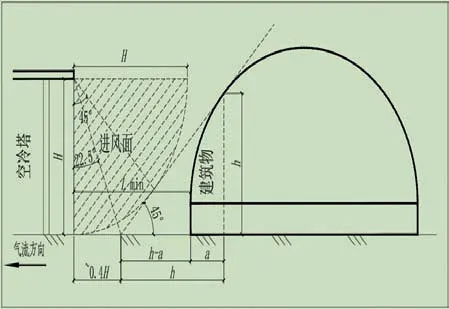
图5 圆弧形建(构)筑物与间冷塔最小避让距离

5 厂址周围地貌和厂区竖向设计对空冷塔的布置影响

厂址周围地貌对空冷塔的布置影响同样需要重视，避免受到高大地物的尾流扰动影响。如山区电厂中空冷塔不宜布置在山头背风面，特别是山头位于主导风向上风侧时严禁背风面布置空冷塔[4]。总平面布置不可避免时，可根据式(2)～(4)合理避让距离。

厂区竖向设计中一般对场地采取一定坡度，从而导致厂区各建(构)筑物室外设计地坪标高存在差异，特别是阶梯式竖向布置的场地中此差异更为明显。场地对间冷塔造成挡风影响主要存在于阶梯式竖向布置的场地。在阶梯式竖向布置的场地中，为降低地基处理工程量，一般情况下间冷塔等大型建(构)筑物宜布置在低台阶挖方区，辅助、附属生产区布置在高台阶填方区。这种布置将可能导致高台阶上布置的辅助、附属设施与高台阶本身高度叠加，对间冷塔进风造成影响。特别是夏季主导风向上风侧上的高台阶上布置较高大的辅助、附属建(构)筑物时会加剧对间冷塔的挡风和动力干扰影响。因此，在总平面布置时，不仅要在平面上保证间冷塔布置的合理性，而且要保证竖向布置的合理性。

冷却塔与直立建(构)筑物设计地坪标高值不同时，式(3)应变为

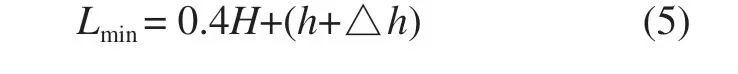
式中：Lmin为空冷塔与建(构)筑物之间最小避让距离，m；H为空冷塔有效进风高度，m；h为建(构)筑物高度，m；△h为建(构)筑物和空冷塔地坪高差值(建(构)筑物地坪高于空冷塔时取正直，反侧取负值)，m。

式(5)的原理如图6 所示。

图6 直立建(构)筑物与空冷塔不同设计地坪时的最小避让距离

冷却塔与圆弧形建(构)筑物设计地坪标高值不同时，式(4)应变为

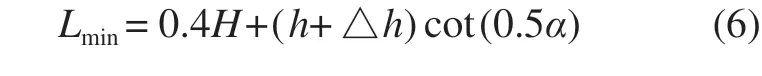
式中：Lmin为间冷塔与圆弧形建(构)筑物之间最小避让距离，m；H为间冷塔有效进风高度，m；H为圆弧形建(构)筑物高度，m；α为圆弧形建(构)筑物间冷塔一侧的平均坡度角值，(°)；△h为建(构)筑物和空冷塔地坪高差值[建(构)筑物地坪高于空冷塔时取正直，反侧取负值]，m。

也可以利用图7 所示几何原理，确定设计地坪标高值不同时的空冷塔与圆弧形建(构)筑物之间最小避让距离。

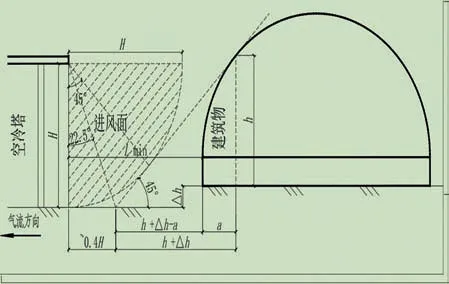
图7 圆弧形建(构)筑物与空冷塔不同设计地坪时的最小避让距离

需要注意的是，不管是建(构)筑物和空冷塔设计地坪是否存在高差，其避让距离仅为总图专业进行厂区总平面规划布置时的最佳距离。因每个电厂所处的气象环境和电厂本身总平面格局均不同，最终避让距离均应通过模拟实验进一步论证。根据实验结果，进一步调整其间距，达到技术经济最合理的结局。

6 结语

火力发电厂中空冷塔为厂区重要的设备及建(构)筑物之一，空冷塔合理的布置直接影响着电厂的效率，对节能降耗起到关键作用。本文中对气流遇到障碍物后的效应进行论述，利用风功率公式对其效应进行论证，进而利用空气流体学原理对空冷岛炉后来风问题、自然通风间冷塔群效应问题、空冷塔与建(构)筑物避让距离公式进行解析，为空冷塔布置提供理论依据和总结其关键注意事项，供业内相关参考借鉴。