斜线槽上游泵送机械密封流固耦合分析*

朱维兵 陈 银 王和顺

(1.西华大学机械工程学院 四川成都 610039；2.中国船舶重庆液压机电有限公司 重庆 402160)

上游泵送机械密封是非接触式机械密封的典型代表，由于其泄漏量小、摩擦功耗低、使用寿命长等优点广泛应用于各种旋转式流体机械中[1]。前人对上游泵送机械密封的研究多数只针对液膜部分，并且假设密封环刚性较大，忽略了液膜压力对密封环变形的影响。实际上液膜压力与密封环端面上的变形是相互影响的，液膜压力增大将导致端面变形量增大，变形量增大相对应液膜厚度就增加，流体动压效应减弱，从而液膜压力就变小，端面变形量也随之减小。如此相互作用，最终达到平衡，这样才符合上游泵送机械密封的真实工况[2]。

国内外学者对机械密封流固耦合的研究开始于20世纪。1996年，YOUNG等[3]以有限元分析法为基础，构建了密封动、静环与流体膜的流固耦合模型,通过数值模拟计算的方法得到了动、静环在不同工况下的温度和变形情况。2003年，LAI等[4]建立了流体静压式机械密封微间隙液膜与密封副的流固耦合模型，考虑了密封端面变形、温度变化、端面粗糙度等因素的影响，并对其进行了单向流固耦合分析。2005年，GALENNE等[5]建立了热-力耦合模型，在机械密封开停车过程中对密封环应力和变形进行瞬态计算，并研究了密封环与流体液膜之间的耦合程度。2008 年，王乐勤等[6]建立了非接触式机械密封流固耦合的物理计算模型，给出了其求解方法，并通过实验分析了密封腔介质压力对密封性能的影响。2011 年，刘向锋等[7]建立了收敛间隙静压机械密封的流固耦合模型，基于雷诺方程，利用 ANSYS Workbench 软件计算密封环的应力和变形，根据自动迭代计算方法进行单向流固耦合分析。2015年，简元霞[8]对经典T形槽干气密封结构进行了双向流固耦合分析，得到了流固耦合作用下固体应力、变形情况和气膜的压力分布规律，以此提出了2种槽型结构优化方案。2016年，李宁等人[9]对螺旋槽机械密封动环进行了单向弱流固耦合分析，得到了动环应力和变形分布情况，然后利用机械密封试验平台进行了对比分析。

在实际工业生产过程中，工作环境一般都是高温高压，甚至高转速，密封环必然会产生变形。因此，为了保证生产运行的安全及可靠性，同时提高生产效率，此时研究液膜与密封环之间的流固耦合作用就显得尤为重要。研究上游泵送机械密封的流固耦合作用，可减少密封研究时限定假设的个数，修正模拟计算所得结果，使所得结果更加贴近于真实情况[10]。同时，研究密封环的应力和变形，可以知晓密封环的工作状态，提前判断是否失效，指导工业设计。

为此本文作者拟建立斜线槽上游泵送机械密封流固耦合计算模型，将其导入ANSYS Workbench中，以Fluent软件流场模拟分析得到的液膜压力作为动环边界条件之一进行单向流固耦合计算，对密封动环的最大应力和最大变形进行分析，为斜线槽上游泵送机械密封的研究和设计提供参考。

1 几何模型的建立

参考文献[11-12]选择斜线槽上游泵送密封端面的结构参数，具体见表1。表中ri和ro分别为斜线槽内半径和外半径，α为径向夹角，β为槽径比，γ为槽宽比，hc为槽深，Ng为槽数，图1所示为密封端面示意图。

采用Pro/E软件，建立斜线槽上游泵送机械密封流固耦合计算模型。因为液膜与槽深都是微米级，为了便于观察，故先将液膜厚度方向和动环槽深方向均放大1 000倍后示出，计算分析时又轴向缩小1 000倍，得到流固耦合三维模型如图2所示。

2 流固耦合基本方程

在流固耦合分析的计算领域中，流体部分和固体部分同时存在，变量包括流体变量和固体变量。因此，其基本方程包括流体控制方程、固体控制方程和流固耦合控制方程[9,13]。

2.1 流体控制方程

(1)连续性方程

(1)

式中：ux、uy、uz分别为x、y、z3个方向的速度分量，m/s；t为时间，s；ρ为密度，kg/m3。

(2)动量守恒方程

(2)

式中:p为流体微单元体上的压力，Pa；τxx、τxy、τxz是指在流体黏性作用下，产生的作用在流体微单元体表面的黏性应力τ的分量，Pa；fx、fy、fz为3个方向的单位质量力，m/s2。

2.2 固体控制方程

(3)

式中:Ms为质量矩阵；Cs为阻尼矩阵；Ks为刚度矩阵；ds为固体的位移，mm；τs为固体受到的应力，MPa。

2.3 流固耦合方程

在流固耦合交界面处，流体与固体应满足守恒方程

τf·nf=τs·ns

(4)

df=ds

(5)

qf=qs

(6)

Tf=Ts

(7)

式中:τf、τs分别表示流体和固体的应力，MPa；df、ds分别表示流体和固体的位移，mm；qf、qs分别表示流体和固体的热流量，W；Tf、Ts分别表示流体和固体的温度，℃。

3 网格划分

网格划分之前，在ANSYS Workbench中对流固耦合模型进行前处理，由于建模时对液膜厚度方向和斜线槽深方向放大了1 000倍，故在网格划分之前，将流体和固体的各个面分别进行定义，主要是流体压力入口面和压力出口面以及流固耦合面的定义，然后在厚度方向上缩小1 000倍尺寸进行网格划分。流体和固体部分的网格应该单独划分，采用ANSYS Workbench对液膜和动环进行网格划分，流体和固体的网格要保持一致，都采用主导六面体网格，且在斜线槽处对网格进行加密，图3所示为液膜和动环的网格图。

4 材料参数及动环的边界条件

4.1 材料参数

为了研究动环材料对其变形的影响情况，文中选择SiC、WC、结构钢YWN8三种材料对斜线槽上游泵送机械密封动环的最大应力和变形进行分析，其弹性模量、泊松比和密度如表2所示。表中E表示材料的弹性模量，μ为泊松比，ρ为材料的密度。

表2 动环材料参数

4.2 边界条件

动环边界条件如图4所示，动环的边界条件包括液膜的压力分布、转速的设置和固定约束面，最重要的就是流固耦合面的设置，选取液膜与动环的接触部分作为流固耦合面。图5所示为当转速n=2 000 r/min，压差p=0.3 MPa时流固耦合面的压力分布云图。

图4 动环的边界条件Fig 4 Boundary condition of moving ring

图5 流固耦合面的压力分布云图Fig 5 Cloud diagram of pressure distribution onfluid-solid coupling surface

5 计算结果与分析

密封动环选用SiC、WC、YWN8三种材料，以不同转速、不同压差下的液膜压力作为边界条件加载到密封动环上对其进行有限元计算。最大应力是机械密封设计和校核的基本依据，最大变形一定程度上决定了其密封性能的好坏[14]。故文中在不同工况参数条件下，对3种密封动环材料最大应力和最大变形进行了分析。

5.1 应力及变形分析

图6示出了3种不同动环材料的应力分布，通过观察发现，3种动环材料的应力分布规律基本一致，故只选取SiC环为例进行分析。由SiC的应力分布图可知，应力从斜线槽内径到外径有逐渐增大的趋势，最大应力发生在斜线槽外径边缘，其值为0.17 MPa，远小于SiC的许用应力130 MPa，符合密封动环设计和校核的要求。

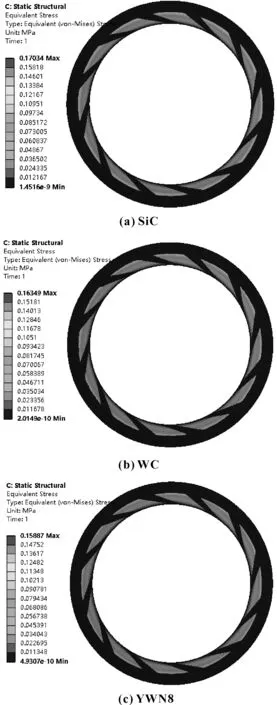
图6 不同动环材料的应力分布Fig 6 Stress distribution of different moving ring materials(a) SiC;(b)WC;(c)YWN8

图7示出了3种不同动环材料的变形分布，可见3种动环材料的变形分布规律也基本一致，同样只选取SiC环为例进行分析。由SiC的变形分布图可知，斜线槽处的变形和应力变化趋势基本相同，最大变形同样发生在斜线槽外径边缘，其值为1.7 μm。而在流固耦合建模时，斜线槽深的取值为5 μm，变形量达到了实际槽深的34%，因此，密封动环材料的变形对机械密封性能的影响是必须要考虑的问题。

图 7 不同动环材料的变形分布图Fig 7 Deformation distribution of different moving ring materials(a) SiC;(b)WC;(c)YWN8

5.2 工况参数的影响

图8所示为不同转速下最大应力和最大变形的变化关系曲线。由图8(a)可知，在压差为0.3 MPa时，最大应力随着转速的增加逐渐减小，动环材料所承受的最大应力由大到小依次为SiC、WC、YWN8；由图8(b)可知，SiC、WC和YWN8三种材料的最大变形量几乎不受转速的影响。这是由于当压差一定时，液膜的压力峰值保持不变，从而传递到动环端面的压力也不变，故随着转速的增加，动环端面所受最大应力和最大变形变化幅度较小。由图8(b)还可发现：WC的最大变形量最小，约为1.6 μm，YWN8的最大变形量最大，达到了2.8 μm，由此可见，YWN8不宜作为动环材料。

图8 压差为0.3 MPa时，不同转速下最大应力和最大变形的变化关系Fig 8 Change of maximum stress (a) and maximum deformation(b)with speed when medium pressure is 0.3 MPa

图9所示为不同压差下最大应力和最大变形的变化关系曲线。可知，在转速为2 000 r/min时，最大应力和最大变形量随压差的增加均呈逐渐增加的趋势，并且最大应力的增长速度更快。这是由于当转速一定时，液膜的压力峰值随着压差的增加而逐渐增大，从而传递到动环端面的压力就越大，因此动环端面所受最大应力和最大变形也越大。

图9 转速为2 000 r/min时，不同压差下最大应力和最大变形的变化关系Fig 9 Change of maximum stress (a) and maximum deformation(b) with medium pressure when speed is 2 000 r/min

综上所述，3种材料相比，YWN8的最大变形量最大，其他2种材料变形较小。同时查阅机械密封相关资料[15]，得到SiC、WC、YWN8三种材料的许用应力依次为130、87、32 MPa。SiC与WC 相比，SiC所承受的最大应力也更大，且具有较强的耐磨性和耐腐蚀性，在机械密封设计时，在同时满足其他要求的条件下，可优先选用SiC材料。

上述研究结果表明：3种动环材料的应力和变形分布规律基本一致，应力和变形在斜线槽处变化较为明显；应力和变形从斜线槽内径到外径有逐渐增大的趋势，且最大应力和最大变形均出现在斜线槽外径边缘。以上分析结果与上游泵送机械密封流固耦合数值分析相关文献结果基本吻合[16]，说明文中仿真计算方法及参数设置是正确的。

6 结论

(1)提出了一种通过ANSYS Workbench软件对上游泵送机械密封进行单向流固耦合计算的方法，这种方法可以推广到水泵、水轮机、压缩机等单向流固耦合的计算，具有普遍适用性。

(2) 在不同转速和压差下对3种动环材料进行了有限元分析，结果表明：最大应力随转速的增加逐渐减小，而最大变形几乎不受转速的影响；压差对最大应力和最大变形影响较大，均呈线性增加的趋势。

(3)通过对比SiC、WC、YWN8三种材料发现：最大应力和最大变形均发生在斜线槽外径边缘处，YWN8最大应力最小，而最大变形最大，不适合做密封动环材料，同时满足其他要求的前提下，优先推荐SiC材料。