基于粒子群的传感器空间覆盖优化方法
张 满,贾云璐,林 杰
(中国工程物理研究院 机械制造工艺研究所,四川 绵阳 621000)
0 引 言
视频监控作为日常安防的重要手段,其在任务区域的有效覆盖率又是评价服务质量的重要指标。目前大多数的研究都是基于传感器网络的覆盖问题,监控摄像机属于传感器的一种类型,所以可以借鉴传感器网络覆盖问题的解决方法展开研究。当前对于传感器网络覆盖控制的研究大多数是基于二维模型[1-4],少部分的三维传感器模型是将三维空间问题约束到二维区域来解决[5-7]。但是由于视频监控任务的特殊性,其需要对一定高度范围内的区域进行较好的检测,例如对于人就需要检测从上到下等一系列特征,基于二维的传感器感知模型及算法不能满足视频监控的任务要求。
该文通过借鉴关于传感器的研究,提出一种适用于监控摄像机的三维模型并通过算法增强监控区域的覆盖度。吴帅[8]与童海燕[9]提出的是一种三维全向的球形覆盖模型,并分别通过粒子群算法与虚拟力算法使得球形传感器在xyz三个方向上均匀分布。作者虽然提出了三维的传感器模型,但是该模型属于全向的模型,由于实际生活中监控摄像机模型的限制,不能直接应用该模型。熊永华[10]通过粒子群智能算法对感知半径可调的有向扇形传感器进行覆盖优化。李娜[11]针对监控区域存在障碍物的情况,引入避障策略,提出基于虚拟力的传感器网络覆盖优化算法。蒋鹏[12]基于二维扇形模型提出了一种虚拟力导向的粒子群摄像头网络覆盖增强策略,结合了虚拟力与粒子群算法来进行传感器的布置。Peng J与肖甫[13-14]使用的是传统的三维传感器模型,作者将关于传感器位姿的方向正交分解为俯仰角和偏向角,在传感器自身参数的限制下,调整单个传感器的俯仰角使得传感器在地面上的投影梯形面积最大化,再通过调整多传感器的偏向角使得传感器的覆盖度最大化。这两篇文献中所使用的传感器节点模型,与视频监控摄像机的任务要求相比较,并不能满足对具有一定高度信息的目标进行检测。
总结已有文献,现有的传感器模型大多都集中于二维平面的感知范围,并没有考虑一定高度范围内的信息获取。针对现有问题,结合监控摄像机的实际情况与上述文献中的传感器模型,该文考虑一定高度的传感器模型,同时假设传感器同构且布置在同一高度平面内,将传感器的布置分为对单个传感器的可视范围最大的俯仰角调整与通过智能算法对多个传感器调整其位置与朝向,最终使得在给定的区域范围内减少重叠区域的覆盖于盲区,提高覆盖率。
1 问题分析
1.1 视频传感器感知模型
参考文献[8]中的球形传感器模型与文献[13-14]中的传统三维模型可得,在三维现实场景中,视频传感器模型可以感知到传感器为中心最大感知距离为半径的球形区域;同时结合实际情况,监控摄像机存在最大水平视角与最大垂直视角的限制,所以将传感器的模型定义为底面为球形其余四个面为扇形的立体图形,如图1所示。

图1 空间感知模型
定义一:传感器模型与参数。
定义二:定义可视区域范围与各坐标点。


图2 有效感知区域
对于单个传感器来说,其偏向角所在平面与俯仰角所在平面相互垂直,调整传感器的偏向角度并不能影响传感器的有效感知区域。因此在传感器高度固定的情况下,影响单个传感器有效感知区域的因素为传感器布置的俯仰角度。
如图3所示,面PD1D2为传感器整体可视范围在坐标系xoz面上的截面,由于传感器可视范围的底面为球形,面PD1D2为扇形。通过调整传感器的俯仰角度影响的是上交面梯形的上下两底之间的距离F1F2与下交面两底之间的距离E1E2,所以该文通过分析在截面PD1D2内,F1F2与E1E2随俯仰角变化的关系,进而分析出最佳俯仰角使得传感器的有效三维感知区域最佳。

图3 三维感知模型截面
1.2 视频传感器的覆盖增强分析
为了方便计算,将监控区域离散化为每隔ΔxΔyΔz选取一个离散点,这样将连续空间覆盖问题就转化为离散空间的覆盖问题。假设空间离散后对应的点集为Ω,所有至少被一个传感器有效空间覆盖的点的集合为Ω',则覆盖区域的覆盖率η定义为:

(1)
假设对区域布撒n个传感器,第i个传感器的参数Ti={pi,Ci}包括传感器的位置Pi(x,y,z),传感器的朝向Ci(λ,θ),则覆盖增强是对所有变量组η(T1,T2,…,Tn)'≥η(T1,T2,…,Tn)。
2 覆盖增强策略
2.1 基于单个传感器俯仰角调节
为了便于研究,同时结合现实世界的设备,假设所有视频传感器同构且布置在相同高度的平面之内。由图4可知,该文通过分析在扇形PD1D2中F1F2与E1E2随俯仰角变化的关系来求得传感器的最佳俯仰角度。
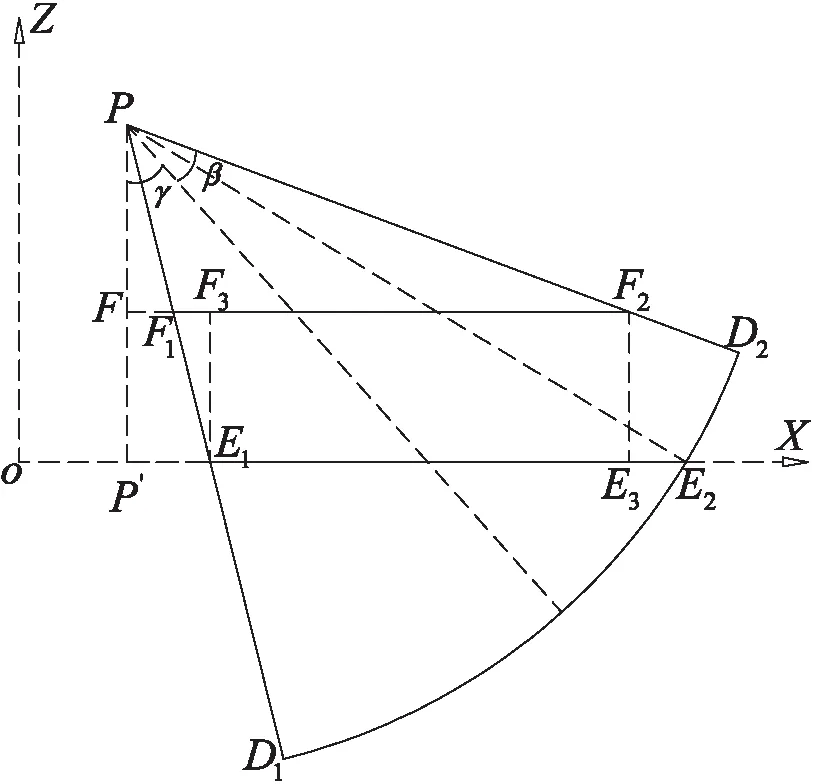
图4 感知模型截面
由于在直角三角形PP'E2中,PP'为传感器的布置高度Z,PE2为传感器的最大可视距离L,这两个值不会随着传感器的俯仰角度的变化而变化。

(2)
F1F2=(Z-H)tan(γ+β)-(Z-H)tan(γ-β)
(3)
由于有效检测区域为竖直空间,所以有效区域为在xoz面上的截面E1E3F2F3,其中:
F3F2=E1E3=(Z-H)tan(γ+β)-Ztan(γ-β)
(4)
通过对上式中的γ求导得:
E1E3'=(Z-H)sec2(γ+β)-Zsec2(γ-β)
(5)
根据实际情况分析,一般布置情况下有(γ+β)>45°,(Z-H)>0.5Z,当(γ+β)>45°时sec2(γ+β)>2,所以有(Z-H)sec2(γ+β)>Z;而(γ-β)的值一般情况下较小,且保持sec2(γ-β)≈1,所以有E1E3'=(Z-H)sec2(γ+β)-Zsec2(γ-β)≥0。
通过分析可得,F3F2与E1E3为随着俯仰角γ的递增函数,当点E3与E2重合的时候,F3F2与E1E3达到最大值,即有效监测区域值最大。
当点E3与E2重合时有:

(6)
通过上述公式可求得传感器节点的最佳俯仰角。
2.2 多传感器位置及偏向角调节
通过俯仰角优化后的传感器空间中的最佳有效覆盖区域如图5所示,进一步调整多个传感器的位置与偏向角度使得对区域的覆盖范围最大化,对于偏向角与位置的优化问题是一个NP-hard问题。粒子群优化算法作为群体智能进化算法,具有求解速度快、质量高等优势,因此将粒子群智能算法引入传感器覆盖增强中[14]。该文以传感器覆盖率为优化目标,通过粒子群算法搜索传感器的全局最优分布,调整传感器的位置与水平方向角来降低重叠感知区域与检测盲区,实现传感器的覆盖增强。

图5 有效感知区域
图中的立体图形的上下两底相互平行,由于图形完全竖直,两底之间的距离为任务要求检测的高度,所以对于图5中的立体图形在空间中的布置可以简化为平面ABCD在任务要求的水平面中的布置。
假设在给定的区域内随机布置传感器数量为Num个,则节点的初始解向量空间为a1(Q11,Q12,…,Q1Num),由于传感器的俯仰角度与高度已经确定,所以a1d=Q1d(x1d,y1d,θ1d)为每个传感器在空间中的水平位置与水平俯仰角。设置粒子群的规模数为n,搜索空间为(a1,a2,…,an)。
粒子i的目标函数为:
fi=η(ai1,ai2,…,aiNum)
(7)
目标函数fi表示对应的粒子ai在Num个传感器下的空间覆盖度。
计算粒子规模内的最大目标函数值并记录为全局最优值:
fmax=max(f1,f2,…,fn)
(8)
粒子群的迭代函数为:
(9)
其中,pid为粒子i的历史最佳情况下的传感器d的位置参数,gad为粒子全局最佳情况下对应的传感器d的位置参数,设初始值为初始情况下的值作为当前每个粒子的最优解,并记录当前位置作为局部最优位置。aid(t)与vid(t)分别为第t次迭代中粒子i的传感器位置参数与位置参数的改变量。ω为惯性因子,体现了第t+1次迭代的vid被上一代vid影响的大小。通过对ω进行改进,使得在迭代初期ω的值基本不变,非常有利于全局搜索。而后期变化缓慢,更利于得到或者接近全局最优值[15]。其中t为当前的迭代次数,r1、r2为[0,1]之间的随机数,c1、c2为学习因子,分别调节粒子历史最优与全局最优的影响程度。
粒子群算法流程如下:
步骤一:初始化节点位置(xi,yi)、数量Num、水平朝向角度θ、区域范围、粒子维度D、规模N、迭代次数,初始化每个粒子,每个粒子是Num个传感器在给定区域的布置,而每个传感器又包括三个维度的解,即每个粒子的解的维度为3 Num。
步骤二:判断是否满足终止条件,如果满足,则算法结束,否则继续。
步骤三:利用式(9)更新粒子群算法中的粒子位置与速度。
步骤四:计算各粒子的目标函数值即区域的覆盖率η。
步骤五:更新各粒子的历史最佳位置和全局最佳位置。
步骤六:返回步骤二。
3 仿真实验及分析

则通过传感器俯仰角调整公式(6)可得最佳俯仰角γ=40.9°,之后求得有效覆盖面的各参数代入粒子群算法。算法训练过程如图6所示。

图6 算法训练过程
通过实验分析,在传感器的初始布置图7中,传感器的布置有些区域较为密集,有些区域则较为稀疏,覆盖率为59.5%。如图8所示,通过PSO算法调整传感器的位置与朝向,传感器的布置均匀,同时覆盖率也提升为82%,覆盖率提升了22.5个百分点,说明通过该算法可以有效地提高传感器在空间中的覆盖率。

图7 初始布置图

图8 调整后分布图
同时在感知区内通过算法调整不同的节点数所对应的覆盖度的变化,由图9可知,当节点数超过80个之后,覆盖率随节点的变化变得缓慢。由文献[14]实现了只调节传感器水平偏向角而不调节传感器位置的算法TDPCA,对比可知,对位置及水平偏向角的调节结果优于只调节传感器水平偏向角的结果。由图中点画虚线还可以得出,只调节传感器水平偏向角的算法结果的波动性较大,这是由于该算法比较依赖传感器布置的初始位置。

图9 不同算法对比
4 结束语
对三维空间内视频传感器覆盖度的增强进行了研究,结合已有模型提出三维有效模型,并将覆盖度优化问题分为水平面与竖直面两个方向。通过任务要求高度与传感器的自身参数确定传感器的最佳俯仰角,而后通过粒子群算法调整多传感器水平方向上的位置及水平偏向角,最终使得多传感器的覆盖度得到优化,并通过仿真实验验证了该算法的有效性。

