基于因果推断肺癌患者预后治疗影响因素研究

周 琦，万亚平,2，左建宏，刘 纯，马真真，杨菁华

(1.南华大学 计算机学院，湖南 衡阳 421001；2.湖南省医疗大数据国际科技合作基地，湖南 衡阳 421001；3.南华大学附属第三医院，湖南 衡阳 421001)

0 引 言

据统计，2018年全世界癌症新发病例为1 810万，其中960万死于癌症。肺癌作为全球最常见的癌症，2018年新发病例为210万，占总数的12%[1]。最近两年因患有恶性肿瘤而死亡的病人逐年上升，虽然在对癌症的治疗上通过手术、化疗、放疗、靶向肿瘤等方面取得了巨大的进步，但肿瘤患者的预后治疗仍然是治疗的难题。周羽等人(2010)应用全自动血细胞计数仪及ELISA法测定血小板计数浓度，说明了血小板与恶性肿瘤之间存在相关性[2]。王菊萍等人(2017)通过对观测数据统计分析得出血小板水平变化与妇科恶性肿瘤的发生发展密切相关[3]。曾在1872年就有学者首次报道过癌症患者的血小板计数增多与恶性肿瘤的侵袭和转移密切相关。1903年，有研究者首次观察到人肺癌细胞周围有血小板聚集[4]。1970年Silvis等人的研究表明，190名肺癌患者中，有60%的患者有血小板增多症[5]。1974年，Tranum等人报道实体瘤患者也存在血小板增多症，另外卵巢癌患者血小板增多症的比例为33%～57%[6]。2015年，Zhang等人在肺癌患者308例病例中，发现有26.6%的患者伴有血小板增多症，晚期癌症与血小板计数增加有关[7]。2014年，Menter D.G认为血小板可能影响了癌症的转移[8]。

虽然癌症患者中血小板增多的发生程度似乎取决于特定的恶性肿瘤，但所有研究的共同发现是癌症患者中的血小板增多可能是预后差和生存率低的标志。在肺癌患者的观测数据中发现引入了更多无关或影响力甚微的因素，早期的研究从观测数据中得出的结论忽略了其吸烟、分期或者化疗等其他因素的影响结果。可能会给临床医生做出无效干预或者误导性干预。为了解决上述问题，该文提出结合因果网络模型分析观测医学数据中的因果识别，利用因果推断模型分析临床资料数据中的因果链路。

1 因果推断的基本理论

数据科学中许多问题都属于因果关系，其目的是了解某种暴露(无论是否随机化)对结果兴趣的影响。即使看似非因果的研究，例如那些以预测和患病率估计为目标的研究，也存在因果关系[9]。为此医学统计学已经通过相关分析方法对医学数据进行了一系列的研究，比如独立样本t检验、方差分析、卡方检验和COX回归比例风险模型分析。但是，这些方法只能理解临床资料中的关联关系，有些关联可能有明显的因果解释，有些可能没有，但是无论如何，统计学本身并不能揭示，具体哪一个变量是因，哪一个是果。

有向无环图定义了变量的概率分布，将因果关系的概念形式化，这一研究重点强调了理解数据生成过程的重要性。而不仅仅表征地观察到变量的联合分布。对数据的因果理解对于能够预测干预的后果至关重要。1763年数学家Thomas Bayes提出了贝叶斯定理，图灵奖得主Judea Pearl将贝叶斯定理发展到了贝叶斯网络，2013年张月等人表述了贝叶斯网络在医学领域的应用研究[10]。Hyvärinen等人(2000)提出了独立成分分析算法(ICA)[11]，使成分在统计上独立，从而获取数据的基本结构。Zhang等人(2009)通过考虑原因的非线性效应，内部噪声效应和观测变量中的测量失真效应，在独立成分分析的基础上提出了后非线性因果模型(PNL)，并证明了该方法在因果方向的可识别性[12]。Shimizu等人(2006)提出了一种线性非高斯非循环模型(LinGAM)，便于从观测数据中识别因果结构[13]。Rosenström等人(2012)使用LinGAM因果发现算法探索睡眠问题与抑郁症中流行病学的因果关系[14]。Helajärvi等人(2014)在探讨观看电视与中青年热体重变化是否有因果关系时同样应用了LinGAM模型[15]。Ma Sisi在2017年的工作中讨论了生物医学中观察数据可用于因果发现[16]。

2 预备知识

2.1 ICA算法

独立成分分析(ICA)目的是找到非高斯数据的线性表现形式，以便成分在统计上独立或尽可能独立，这样表示能够捕获许多应用程序中数据的基本结构。比如：特征提取和信号分离。假设观察到n个独立分量的n个线性混合物x=(x1,x2,…,xn)，则有：

xj=aj1s1+aj2s2+…+ajnsn

(1)

在ICA模型中，假设每个混合xj以及每个独立分量sk都是随机变量，观测值xj(t)则是该随机变量的样本。在不失一般性的前提下，可以假设混合变量和独立分量均具有零均值，如果不是零均值，就将观测变量xi通过减去样本均值而居中，从而使模型为零均值。在式(1)中用A表示具有元素aij的矩阵，可以说，

A=[ai1,ai2,…,ain]T

式(1)的混合模型可以转化为：

x=As

(2)

式(2)是一个生成模型，也就是ICA模型，描述了如何通过混合分量si的过程来生成观测数据。独立分量是潜在变量，这意味着它不能被直接观察到，混合矩阵也是未知的，观察的只是随机变量x，需要通过x来估计A和s。

2.2 LiNGAM模型

LiNGAM算法是用于从非实验数据中发现因果结构的方法，对数据生成过程做了各种假设，以便从纯粹的观测数据中进行识别因果关系。给定一个m*n的观测数据矩阵X，且m≪n,采用ICA算法获得分解的X=AS，得到连接矩阵Y(Y=WV)的线性变换矩阵W，把W按照严格下三角的W矩阵进行排序，得到下三角的W矩阵，通过LiNGAM算法进行因果发现网络次序。线性非高斯非循环模型，在结构方程模型(SEM)的基础上引入三个假设，即：

(1)观测变量xi，i∈{1,2,…,m}可以按照因果顺序排列，这样后面的变量无法影响前面的变量。用k(i)表示这样的因果顺序。也就是说生成过程是递归的，这意味着它可以用有向无环图(DAG)以图形的方式表示。

(2)分配给每个变量xi值是已经分配给较早变量值的线性函数，加上一个“干扰”项也就是噪声项ei，以及一个可选常数ci,即：

(3)

(3)干扰变量ei是所有具有非零方差的非高斯分布的连续值随机变量，并且ei彼此独立，即：

p(e1,e2,…,em)=∏ipi(ei)

(4)

使用Wald统计信息检验边的重要性，用于测试观测到的变量xi是否具有统计学意义。定义用于整体模型拟合的测试统计量：

模型的阶矩结构：由基于模型的协方差元素组成。

σ2(τ)=νec+{E(xxT)}

(5)

与式(5)矩对应的样本定义为：

(6)

通过m2估算σ2(τ0)≈m2，其中τ0表示真实参数向量。

3 基于LiNGAM的肿瘤患者临床数据因果发现方法

分析肿瘤患者癌症预后情况时，影响癌症预后的因素繁多且关系复杂，从观测数据中仅仅只能通过相关分析，发现具有简单统计学意义的因素之间的关联关系。该文利用LiNGAM算法可判断观测变量间的因果关系，指明因果方向及其链接强度。在LiNGAM的假设情况下，仅凭基础观测资料就能确定因果结构。

一般对于肿瘤患者的基础临床统计数据包括：年龄，分期，化疗、肿瘤大小、血小板计数、白细胞计数、生存时间等基础指标。观察数据矩阵X，每一列包含一个样本矢量xi，以分期、血小板和生存时间为例：从相关分析的角度可以得出，分期与血小板计数之间存在相关关系，分期与生存时间之间存在相关关系，血小板与生存时间存在相关关系，其关系网络如图1所示。

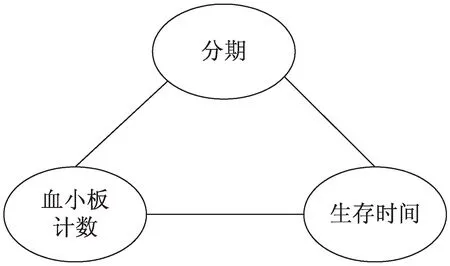
图1 假设的三个变量的关联图

从图1中只能观察到三者之间存在关联，却并不知道其因果方向以及链接强度，因此不能判断血小板计数是否能够作为预后评估的可靠标志物。基于LiNGAM肿瘤患者临床数据因果发现方法，通过对医学数据生成模型的假设，从观察变量中学习到数据的协方差矩阵，从协方差矩阵中计算所有条件相关性，估计完成的因果结构。简单来说以上3个变量可以表示为：

图2是假设的数据生成模型，e1、e2、e3表示干扰的噪声项，?表示链接强度的权重。如果观察到足够数量的数据向量x，就可以识别出包括所有参数在内的完整因果结构。LiNGAM算法的具体实现为：

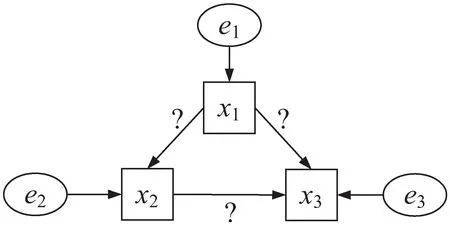
图2 在LiNGAM假设下的数据生成图

算法1：LiNGAM的因果发现方法。

输入：数据矩阵X；

输出：估计观测变量之间的链接强度矩阵B，估计的变量之间的因果顺序K和因果关系网络图。

(1)根据公式(1)、公式(2)，计算数据的ICA分解估计独立分量，计算混合矩阵A和分离矩阵W(W=A-1)，其中干扰变量ei对应W的行，观测变量xi对应W的列。

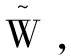
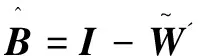
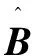
(6)返回因果顺序K以及可视化变量之间的因果网络。

算法2：基于LiNGAM的肺癌患者临床数据因果发现方法。

(1)输入肺癌患者观测数据X1，包括分期、化疗、血小板计数和预后生存时间。

(2)LiNGAM模型分析出四者的因果关系图。

(3)找到对血小板计数和生存时间的共同因素是分期和化疗。

(4)先对化疗进行控制，重新输入观测数据X2，包括分期、血小板计数和预后生存时间。

(5)LiNGAM模型分析出三者的因果关系图。

(6)再对分期进行控制，输入观测数据X3，仅仅只包括血小板和生存时间。

(7)LiNGAM模型最终得出血小板和生存时间的因果关系。

4 实验与分析

4.1 数据处理

本实验选取了2012年01月至2017年12月期间在南华大学附属南华医院和南华大学附属第一医院就诊的肺癌患者231例，随机选取南华大学附属南华医院体检中心健康志愿者83例纳入健康组，观测到患者的年龄、血小板计数、分期、吸烟、化疗以及患者的预后生存时间。在此之前已经对数据进行了筛选，选择的标准为纳入标准：(1)所有的患者病理诊断明确；(2)肿瘤专科治疗前均接受头胸腹部增强CT或MRI、全身骨扫描等检查以明确临床分期；(3)临床资料完整，可提供肿瘤专科治疗前的血常规检查结果、肿瘤标志物、影像学资料等；(4)无合并有妊娠或哺乳、血液系统疾病、自身免疫性疾病(如特发性血小板减少性紫癜)等疾病；(5)所选病例死亡的直接原因与肿瘤有关。

4.2 模型实验分析

本研究基于LiNGAM算法生成肺癌患者临床数据之间的因果关系图，利用ICA算法判断因果关系图中边的存在性，设置显著性大小为0.95。

根据对观测数据的初步分析，对肺癌患者的血小板计数和健康志愿者的血小板计数分别做了相关的统计，如图3所示。

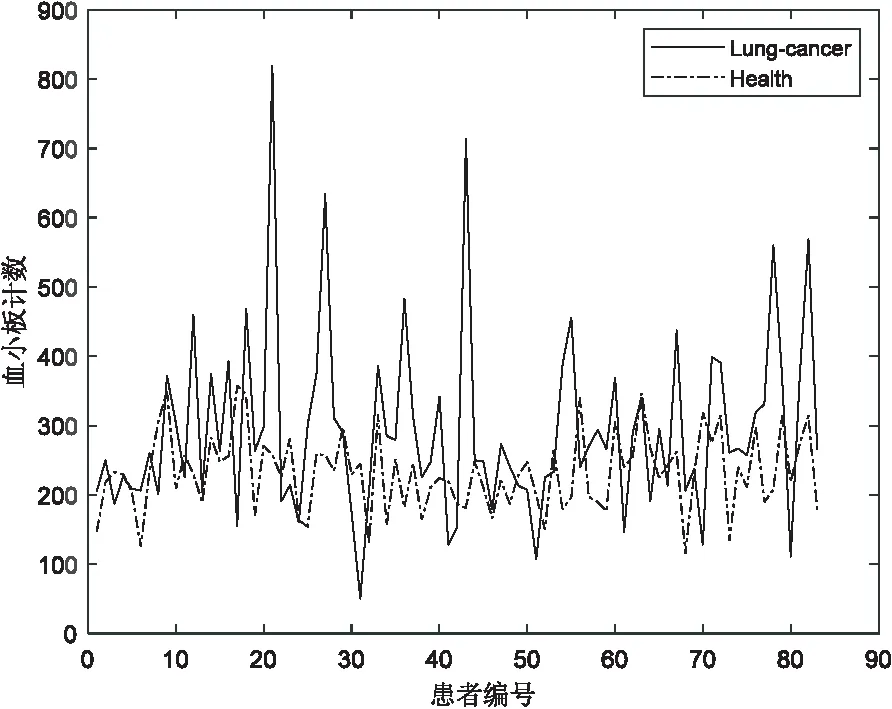
图3 患病与健康的血小板曲线图

从图3中可以很明显看出肺癌患者的血小板计数高于健康人的血小板计数，这符合前人研究的癌症患者通常伴有血小板增多症的现象。

从观测到的肺癌患者临床资料中采集到的分期、化疗、预后生存时间和血小板计数4个指标，基于LiNGAM算法构建因果网络模型，得到患者的预后因素因果关系图，如图4所示。

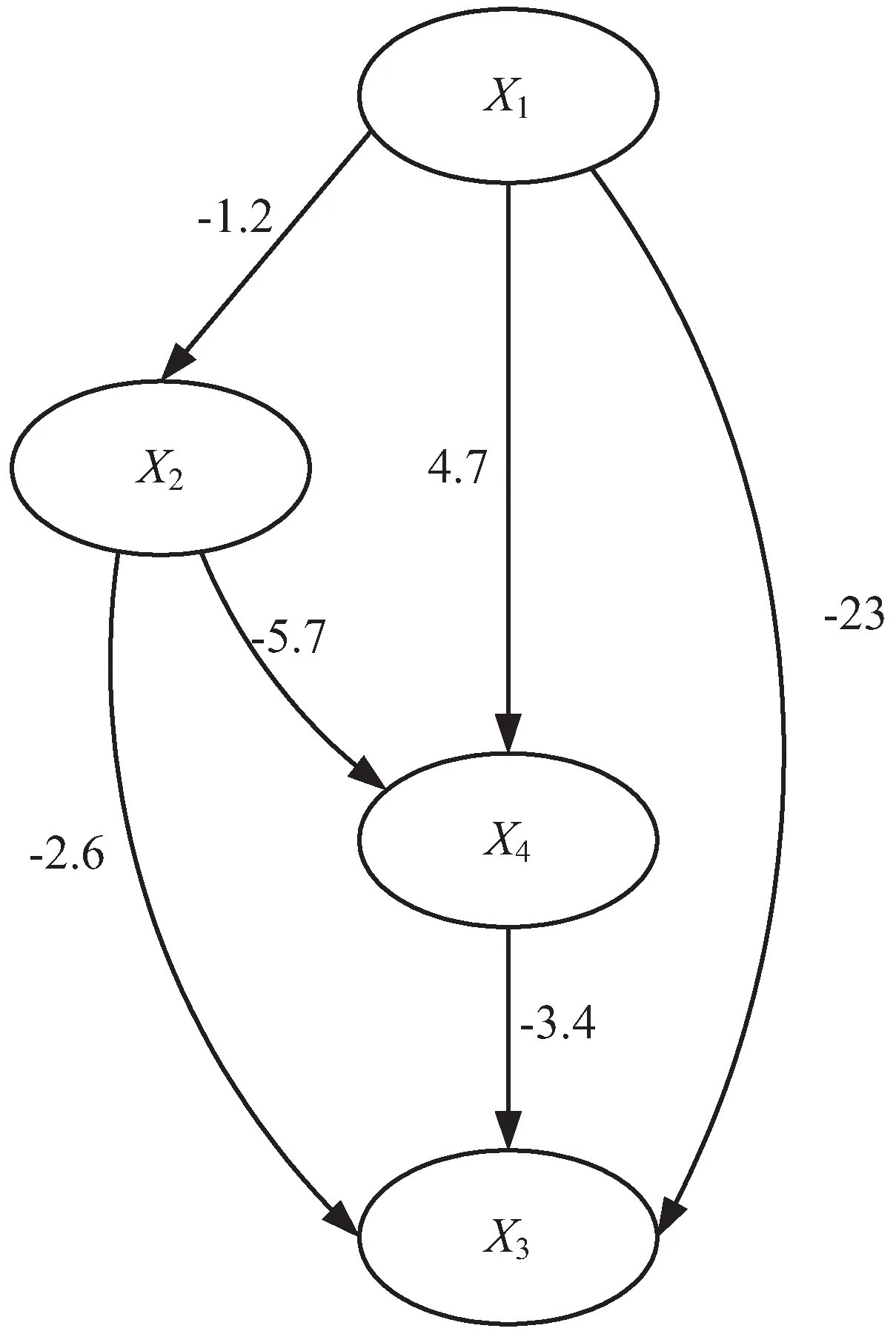
图4 四个变量之间的因果关系图

在0.95的置信水平下，肺癌患者的预后生存时间受血小板计数、癌症分期和化疗的影响。并且分期对生存时间的影响较大，血小板计数对预后生存时间有直接影响，化疗和分期是血小板和生存时间的共因，在单独考虑血小板对生存时间的关系，应该对化疗这个因素予以控制。

在95%的置信区间下，对化疗这个因素进行控制，选取接受化疗的患者的分期、血小板计数和预后生存时间。

在0.95的置信水平下，肺癌患者的生存时间受血小板计数和癌症分期的影响，其中分期是血小板计数和生存时间的共因，图4中分期对血小板计数的因果强度增大了，血小板计数对生存时间的因果强度同样也增大了。同上，在做过化疗患者中对分期指标进行控制，分为I、II、III、IV期，显著性大小同上，得到的结果如图5所示。

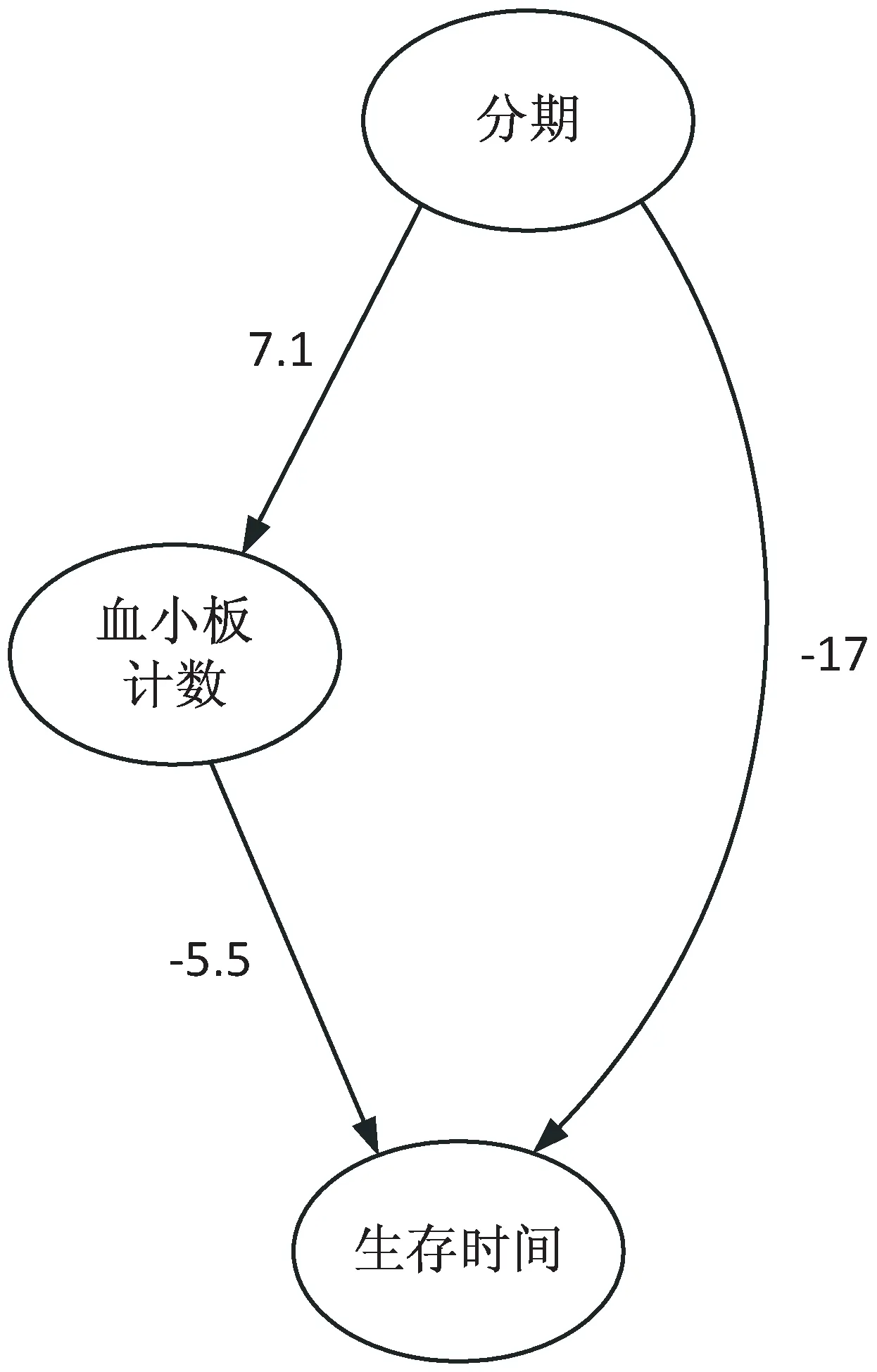
图5 三个变量的因果关系图

从图6中可以直接看出血小板对生存时间的影响关系及影响程度，符合临床上血小板与恶性肿瘤相关联的合理性。血小板可以作为肺癌患者生存预后的一个检测指标。

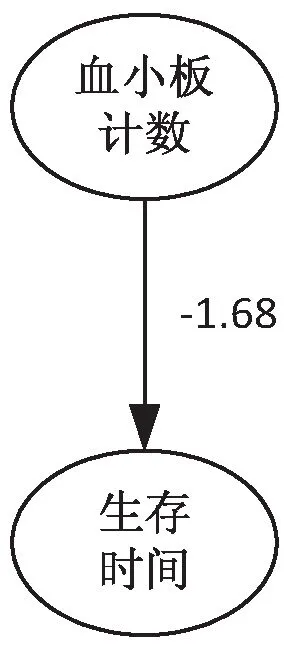
图6 血小板与预后生存时间因果关系图

该文研究采用SPSS(statistical product and service solution)软件对肺癌患者中接受化疗的患者相关数据值进行相关分析。据相关分析结果显示(如表1所示)，表明分期、血小板计数与患者的预后生存时间存在一定的关系，与模型结果吻合。

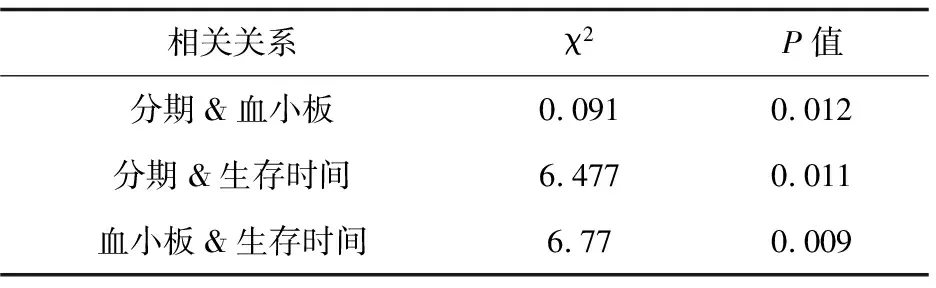
表1 相关分析结果

5 结束语

针对肺癌患者预后治疗差患者生存率低，准确判断肿瘤预后治疗的影响因素之间的关系变得尤为重要。该文提出了基于LiNGAM模型肺癌患者的临床数据因果发现方法。从因果推断的角度出发，对医学观测数据中肺癌患者预后治疗的影响因素分析，准确判断患者预后，为临床治疗提供有效的干预。实验结果表明该方法能够识别肺癌患者预后治疗影响因素之间内在因果机制，血小板可以作为肺癌患者预后评估的一个检测指标，同时也为因果推断的应用领域提供了新的研究方向，为医学观测数据的因果识别提供了新的工具。