虾塘差速无人投饲船巡边算法设计与仿真分析
胡庆松,陈研霖,陈普坤,陈雷雷,匡兴红
(1 上海海洋大学工程学院,上海 201306;2 上海海洋可再生能源工程技术研究中心,上海 201306)
随着对虾养殖行业的转型升级,无人投饲船已经日渐成为对虾养殖生产作业自动化的重要装备。作为典型的无人投饲船,差速无人投饲船以其航行稳定、运动灵敏、易于控制等优点广泛应用于虾塘养殖作业[1]。结合对虾沿边巡游的摄食习性,巡边作业及其控制算法的研究能为虾塘差速无人投饲船设计与应用提供理论依据。
巡边算法是国内外学者关注的研究热点之一。Yata等[2]在无人小车平台上研究了单超声传感器巡边控制,提出了巡边过程的部分控制参数,并指出了其巡边算法在速度方面的局限性。在此基础上,Suresh等[3]应用图像采集技术和多传感器融合算法获取巡边控制中相对精确的姿态信息;Wei等[4]提出了一种基于实时动态虚拟墙的巡边控制方法,能在航行速度0.6 m/s的限定下,较好地完成巡边作业。随着硬件技术及智能算法的发展,Teng等[5]利用视觉技术建立边界特征来捕捉边界信息,在光照条件稳定的室内场景中研究了其巡边算法的应用效果。Lin等[6-7]基于人工蜂群的自适应神经网络控制算法,以巡边过程的角度和距离信息为控制量,采用仿真方法验证了该算法在速度小于1 m/s情境下的性能。Chen等[8-9]用模糊神经网络改善了人工蜂群算法,提高了对边界的适应性。Jhang等[10]比较了模糊1型和2型算法在巡边控制中的应用,指出了模糊2型算法在实时计算方面具有较好的性能。考虑实际环境中干扰因素对巡边作业的影响,Wang等[11-12]通过设计干扰观测器来估计环境产生的干扰项,应用反步控制器生成控制律来解决一定范围内的扰动问题。
综上,巡边控制算法的研究取得了一定的成效,但主要集中在低速无人船巡边作业领域,且硬件成本高、实现过程复杂,无法满足虾塘差速无人投饲船的巡边作业要求。虾塘差速无人投饲船应用中,要求在较低成本下,较大运行速度范围内,实现船体在水面颠簸摇晃的环境下稳定、可靠的巡边控制作业。
本研究在差速无人投饲船运动模型的基础上,提出了一种以带夹角的双超声或双红外传感器为感知设备,融合传感器数据和传感器安装角度信息构造船体姿态三角形,通过利用边距(边距区间搜索控制)和船体姿态角(PID算法控制)实现投饲船巡边的PID巡边控制算法。并在MATLAB环境下建立仿真模型,仿真验证了方塘和不规则塘边界下不同速度时,算法的适用性和姿态保持的稳定性。
1 差速无人投饲船运动与反馈模型
1.1 差速无人投饲船运动模型
差速控制是投饲船最常见的船体运行控制方式之一[13]。差速无人投饲船在投饲作业中,首先,不同池塘面积和养殖阶段对投饲量需求有较大的不同,要求算法能在较高速度(2~3 m/s)下稳定运行,以提高养殖生产作业的柔性;其次,水面投饲作业工作环境湿度大、粉尘多[14],要求算法的基础感知设备具有恶劣环境适应性及可靠性;最后,农业生产具有成本敏感性,要求算法整体的软硬件成本较低。
差速无人投饲船如图1所示,一般由左右2个螺旋桨推动船体运行,通过左右螺旋桨差速来控制船体左转或者右转,实物模型如图1所示。
毛鸡随着只重的增大,其腿、大胸等部位的占比会随着相应的增大。由图1毛鸡只重对肉鸡腿产品的出成影响可知,随着鸡只毛重从4.31×500g增加到5.91×500g,腿出成变化非常明显,从25.41%增加到26.29%,增加了0.9%。不同毛鸡只重对于腿产品的出成有明显的影响,并且4.61×500g和5.10×500g两组实验中腿出成变化趋势大,腿出成相差0.6%,对于提高腿类出成的毛鸡只重在5.00×500g以上效果显著。

图1 双体船实物图Fig.1 The structure of Twin-Hull
根据其运行特性,在忽略俯仰、横摇、纵摇运动自由度的情况下[15](一般在恶劣天气环境下,投饲作业会暂停,可以忽略风浪和恶劣天气的影响),可以在图2所示坐标系中定义差速无人投饲船的运动模型,表示为公式(1):

图2 投饲船模型坐标系定义Fig.2 Coordinate system definition of the feeding ship model
(1)


(2)
1.2 差速无人投饲船的运动姿态反馈模型
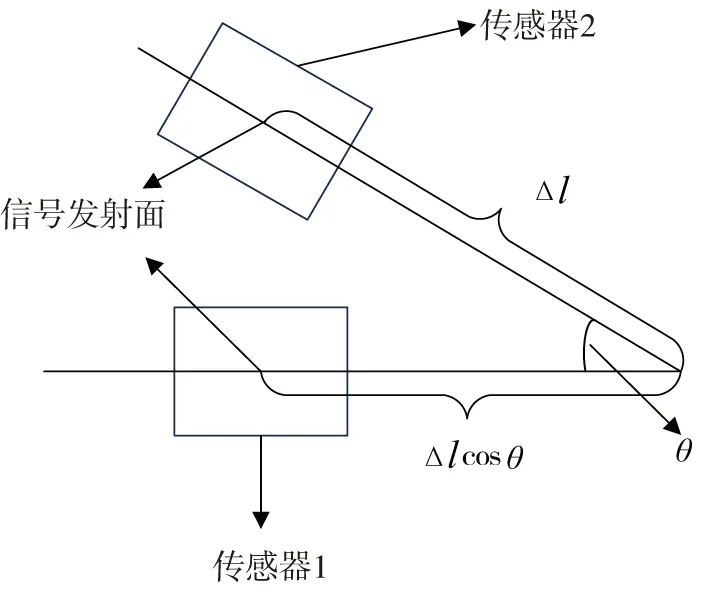
船体位置信息是船体运动闭环控制的重要因素,减少其信息反馈量,能够大幅简化控制器设计[16-17]。差速无人投饲船姿态反馈模型通过2个传感器反馈的距离信息及传感器安装位置信息计算船体位置信息。如图3所示,所搭载传感器按照水平角度θ安装在靠近边界一侧,传感器1的信号发射方向需垂直于船体边沿,根据实际应用环境不同,可在船头选择合适的位置。

图3 传感器安装位置示意图Fig.3 Schematic diagram of sensor installation position
将传感器距离信息和安装角度结合,可得到船体运行的姿态三角形Δoo1o2,如图4所示,边界l可反映船体的边界信息。
边界l与船体边沿平行时,姿态角α=90°,为船体正确姿态。当姿态角α>90°时,船有远离边界的趋势,如图4a所示,控制系统应向靠近边界侧响应。当边界l延长线与船左侧边沿相交且成锐角,姿态角α成锐角,此时控制系统应输出远离边界的响应,响应程度大小取决于实际偏差,如图4b所示。通过不同状态下的姿态三角形可得到巡边无人投饲船在池塘中的位置信息。
船体的定位方式采用相对定位[18]。在传感器进行合理布置后,通过传感器反馈的距离信息计算姿态三角形参数并得到控制参量。边界l满足:l=(d12+d22-2d1d2cosθ)1/2,同时可得到姿态角α=arccos((l2+d12-d22)/2ld1)。如图4所示,D为姿态三角形的高,表示船在航行过程中与边界的距离关系。在实时控制中,考虑到传感器的反馈误差,为提高计算精度,选用两个传感器反馈值的较小值进行D的计算,不同姿态时,D分别满足以下公式。
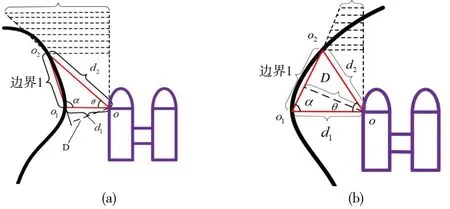
图4 船体与边界的相对姿态Fig.4 Relative attitude between hull and boundary
当d2>d1时,
(3)
当α≤90°,θ≤90°,α+θ≥90°时,
(4)
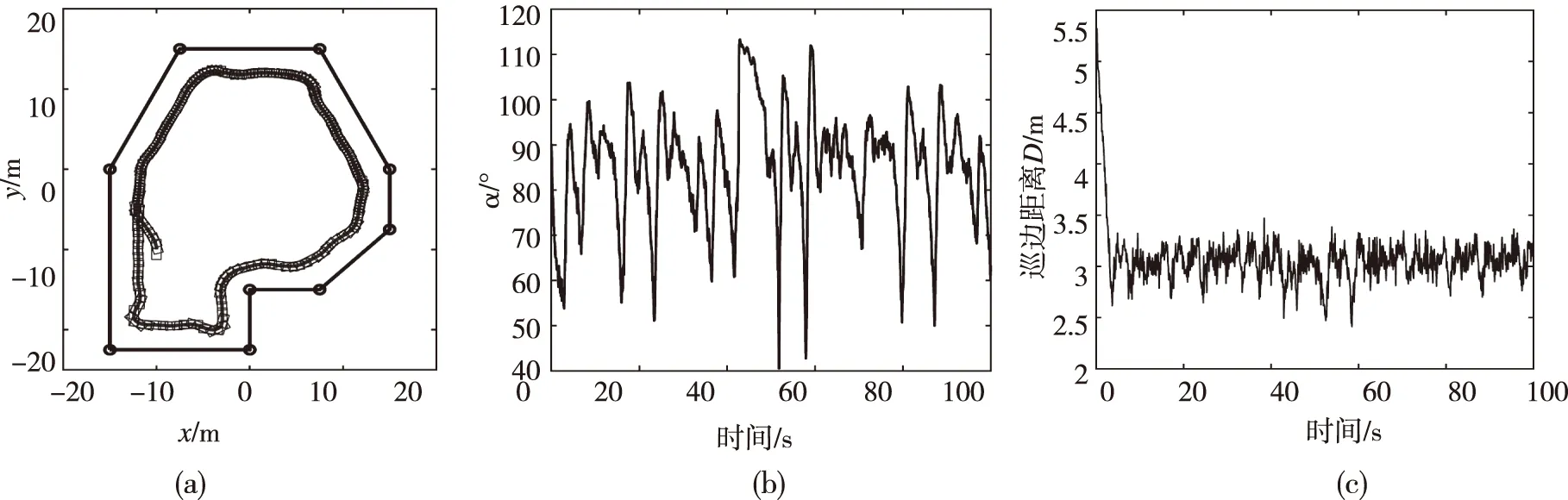
当d2 D=d2sin(θ+α) (5) 式中:d1、d2分别为传感器1和2的反馈距离;l为三角形边界;α为姿态角。 巡边作业过程中,参数选择的差异会影响边界跟踪性能,因此,安装角θ、航行速度v、巡边距离L这3个参数在调整中应遵循如下几个原则:1)巡边速度较慢时,安装角θ和巡边距离L,可有较大的选择范围;2)巡边速度较快时,为减少反馈信号的干扰,安装角θ应选较大值;3)为减少传感器相互干扰,安装角θ应尽量选择大于45°的角度值;4)进行较大巡边距离跟踪时,应结合安装角θ考虑传感器的距离量程。根据以上原则,参数选择范围示例如表1所示。 表1 安装角θ、航行速度v、巡边距离L技术参数Tab.1 The parameter of θ、v、L 为较快收敛到PID姿态控制范围,设计了边距区间搜索控制律以控制船体的距离。边距区间搜索控制通过划分误差区间确定控制量,区间大小根据MCU计算能力及控制平滑性要求划分参考调整策略如表2所示,表2中有3种区间:L(大范围)、M(中间范围)、S(小范围),2种控制策略:左(TL)、右(TR)。图5为区间搜索的控制过程,算法会最终收敛到PID控制。调整区间根据两传感器信息的相对关系确定,表2中d1、d2的相对长度应根据安装角度θ确定,正确姿态时满足式(6),同时对应PID控制区间。 图5 边距区间搜索控制律Fig.5 Margin interval search control law 表2 船体运行范围控制枚举表Tab.2 Enumeration table of hull operation range control d1=d2cosθ (6) 因传感器类型或安装方式不同,会造成返回距离计算的固有误差,从而影响巡边控制的精度。为了尽量减少这种影响,引入修正量Δl,Δl为传感器2探头到超声波反向交点的距离,如图6所示,式(6)变更为式(7)。 图6 传感器安装误差示意图Fig.6 Schematic diagram of sensor installation error d1+Δlcosθ=(d2+Δl)cosθ (7) 2.2.1 PID控制的实现 变积分PID算法基本公式见式(8),在无人投饲船巡边PID算法中,被控量为姿态角α,船体航行姿态的控制是在电机设定的转速的基础上对转速进行微调,每个电机的实际转速可以表示为设定转速和微调转速,驱动电压由基础电压U和调整电压ΔU组成,改变ΔU,将改变姿态角α的大小从而改变船体前进的方向。所设计PID姿态控制算法,为减少硬件负担并更好地满足实时性控制要求,采用变速积分PID调节和增量输出。 e(k)}T+kd[e(k)-e(k-1)] (8) 式中:e(k)、e(k-1)—分别表示当前和上一时刻的控制偏差;Kp—比例系数;Ki—积分系数;Kd—微分系数;T—控制周期。其中f[e(k)]满足下式: (9) 式中:N、M—分别为关于偏差的分离区间上限和下限。 为防止积分饱和,对积分环节输出限幅,设置输出上限Umax和下限Umin,当u(k)满足Umin 2.2.2 关键参数的选择 1)采样周期的选择 2)控制参数的选择 仿真应充分结合实际被控系统物理特征[23],如螺旋桨输出延时、功率放大器响应滞后、信号噪声等因素。在MATLAB/SIMULINK仿真环境下,以一阶惯性环节模拟延时过程[24],用方差为1.3、均值为0的高斯白噪声代表传感器信息的不确定性[25],综合实际硬件系统各环节衔接产生的控制延时,将采样频率设为10 Hz[26-29]。 3.1.1 方塘边界仿真试验及分析 矩形边界是对虾养殖池塘最常见的边界形式,边界立面呈斜坡状或垂直状。仿真船速为3 m/s,要求保持的巡边距离为3 m。仿真结果显示见图7,由曲线b可见姿态角α总体保持在90°,在边界拐角处出现的较大的波动,表明算法能够保证姿态的稳定性;曲线c可见巡边策略能够保持参考距离D的总体稳定性,当出现较大拐角时,距离并没有出现较大的偏差。 图7 矩形边界仿真跟踪结果Fig.7 Simulation and tracking results of rectangular boundary 3.1.2 不规则塘边界仿真试验与分析 考虑养殖池塘实际状况各不相同,为验证算法的适应范围,建立如图8a所示不规则边界并进行仿真验证。仿真船行速度为3 m/s,巡边距离为3 m,结果显示,在相对较复杂的边界下,姿态角存在一程度的波动,但算法仍能保持距离和姿态的稳定性。从边界角度看,本研究所提算法和文献[9]都表现出对不规则边界较好的追踪效果,相比而言,通过强化学习增强了算法优化方面的优势,但同时提升了对传感器数量和数据处理的要求,增加虾塘环境中设备维护的负担。 图8 不规则内凸边界仿真跟踪结果Fig.8 Simulation results of irregular inner convex boundary 在不规则边界条件下,要求相同的巡边距离,对不同的安装角θ和巡边速度进行仿真对比分析,以验证算法对不同的安装条件和船行速度的适应性。安装角分别取30°、45°、60°、80°,在船速取2 m/s时仿真结果见图9,可见不同的安装角下,巡边距离可维持在设定距离3 m,同时在30°时遇到拐角出现较大偏差,但算法的收敛速度较快,能够很快恢复到正常范围,姿态角维持在90°附近。巡边速度取0.5、1.0、1.5、2.0 m/s,安装角取60°时,仿真结果见图10,可见不同的船速下,船的位姿保持在正常范围内。方差分析结果显示,不同安装角下,姿态角α的波动方差依次为0.036、0.031、0.038、0.047;不同巡边速度下,姿态角α的方差依次为0.12、0.08、0.04、0.05。方差分析显示,两组参数的仿真结果数据波动小,即在不同的船速和安装角度下,算法能够保证船体的巡边运行的稳定性。文献[4,9,30]仿真分析距离等参数对所提算法的影响,综合相关文献结论显示,在室内环境下,最大巡边速度为2.92 m/s,可保持的稳定巡边距离为0.74 m。相比之下,本研究算法具有装置安装参数可调的优势,对于较快速的巡边过程具有一定的可靠性。 图9 不同安装角下的距离和姿态角图Fig.9 Distance and attitude angle diagram under different installation angles 图10 不同船速下的距离和姿态角图Fig.10 Distance and attitude angle diagrams at different ship speeds 差速无人投饲船巡边控制算法是虾池塘养殖自动化装备设计和应用的关键。本研究基于差速无人投饲船的运动特性,构建了基于三角形参数的姿态反馈模型,解决了姿态解算计算量大的问题。结合模型,提出了一种融合测距传感器数据的巡边控制算法,降低了双体船运动控制中非线性因素的影响。充分考虑到算法转化为工程实际的难度,其实现过程受不同环境的影响较小。仿真结果表明,算法在0~3 m/s的速度设定下,能满足0~3 m的稳定巡边距离要求。同时,算法对具有内凹角和外凸角的边界具有相同的追踪效果,表现出不同类型边界较好的适应性。综上,在算法设计和实现方式上,本研究对巡边过程的实际应用都有一定的借鉴意义。为了进一步增加算法的适用范围和可靠性,在后续的研究中,将考虑风浪、障碍物等因素的影响,探索不确定环境下的巡边控制及路径重规划问题。 □
2 巡边控制律设计
2.1 边距区间搜索控制律


2.2 PID控制算法

3 仿真分析
3.1 池塘边界仿真分析

3.2 速度与安装角仿真分析


4 结论

