轨道交通车辆全胶条密封车窗结构胶条接触应力计算
徐 涛 朱红茜 胡小玲 王金辉
(1.中国中车青岛四方机车车辆股份有限公司,山东 青岛 266111;2.湘潭大学土木工程与力学学院,湖南 湘潭 411105;3.株洲时代新材料科技股份有限公司,湖南 株洲 412007)
随着轨道交通行业的发展,列车速度不断地提高,车窗承受的空气压力和摩擦力也不断地增大[1],对车窗安装方式提出了更高的要求。目前,列车的车窗安装方式主要有全胶条安装固定连接、机械啮合固定连接、机械啮合和黏合剂黏接相结合连接、黏合剂黏接等。其中,黏接剂黏接在高速动车中应用最为广泛[2],黏结剂黏接车窗能够有效保证列车行车的安全性、舒适性和气密性[3-5]。但是车窗更换时间长,无法快速更换。全胶条安装固定连接(即全胶条密封车窗结构)是最为简洁的一种,该结构无密封胶密封,维修便捷,只需要几十分钟就可以快速完成车窗的更换[6]。然而,全胶条密封车窗存在漏雨问题。该文以全胶条密封车窗结构为研究对象,对全胶条密封车窗漏雨情况进行力学分析;通过理论计算了密封胶条接触应力与接触长度设计值应满足的关系,确保车窗不漏雨最后,将该文提出的方法应用到具体案例中,并利用ANSYS有限元软件开展了数值模拟,对理论分析结果的可行性进行了验证。
1 全胶条密封车窗不漏雨条件分析
轨道交通列车的全胶条密封车窗结构的连接示意图如图1(a)所示,车窗仅通过胶条安装到车体上,胶条与车体和车窗的接触面上有足够的密封力是保证车窗不漏雨的关键。假设车窗安装完好,车窗在行驶过程会受到外部风、雨载荷的作用,由于车窗尺度相对于外部压力变化的特征尺度很小,因此可将这些载荷设定为均布载荷q0。要保证车窗在q0的作用下不漏雨,首先进行定性分析。任取一剖面,对其进行受力分析,如图1(b)所示。胶条与车窗和车体分别都有内外2个接触面。当车窗外侧受载荷q0作用时,胶条变形,并发生微小的偏转,车窗整体往车内侧偏移,偏移严重时,可能使车体外侧与胶条接触面脱开,导致车窗漏雨。
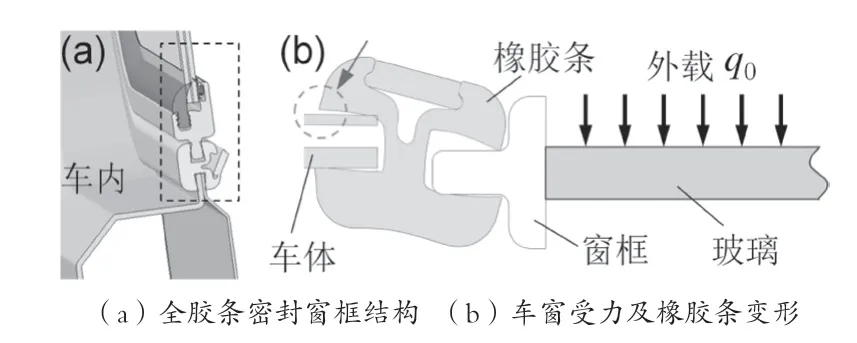
图1 全胶条密封车窗及受力示意图
设胶条对车体外侧的密封力为F外,内侧密封力为F内,如图2所示。无均布外载时,F外=F内。有均布外载荷q0作用时,q0会在胶条与车窗和车体的4个接触面上产生附加力F(q0) 。由于车体外侧最有可能漏雨,下面仅关注胶条与车体的密封力。由受力平衡知,胶条对车体内、外侧的密封力发生了变化,力的平衡方程如下。

由图1的分析结果可知,无论在车窗外侧有多大的外载作用,只要车体外侧不脱开,即只要胶条对车体外侧的密封力F外始终大于0,就能保证车窗不漏水。由方程(1)可知满足车窗不漏雨的条件如下。

要保证公式(2)恒成立,则:

通过定性分析,由(3)式可知,为确保车窗不漏雨,设计胶条尺寸时,需要使胶条对车体的密封力设计值(内、外侧的力相等)始终大于外载在该处产生的附加力的最大值即可。
2 外部载荷作用引起的胶条与车体接触面上的附加力计算
在外部载荷作用下,由于胶条的偏转,车窗相对于车体产生微小的转动,如图2。因此,胶条对于车窗的约束可以看作是固定铰链支座。当q0作用于车窗玻璃上,在胶条约束处会产生附加的作用力F(q0),从而引起胶条对车体和车窗密封力的变化,甚至导致胶条与车体脱开。根据不漏雨条件分析结果,只要外部载荷q0在胶条与车体外侧引起的附加力F(q0)始终满足公式(3),就能保证车窗不漏雨。为求解F(q0),可将胶条约束的车窗结构简化为四边简支的薄板结构进行分析,如图3所示(垂直于玻璃窗方向观测)。在外界均布载荷q0的作用下,四边简支支座反力即为作用力F(q0)。
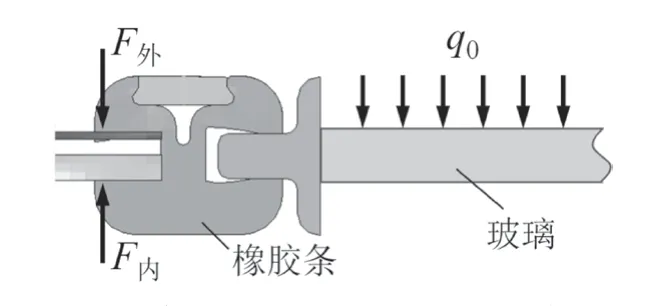
图2 车窗胶条与车体接触面上的密封力及外载示意图
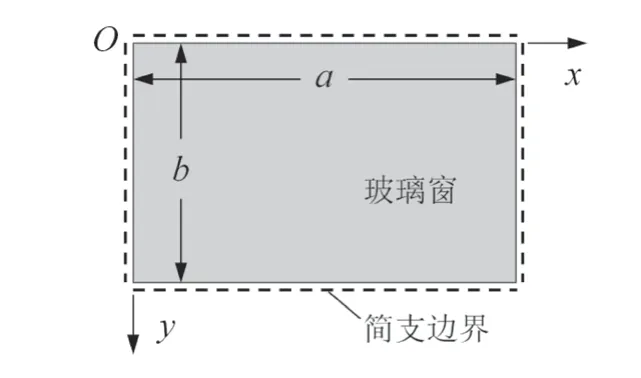
图3 全胶条密封车窗简化的四边简支薄板结构
如图3所示,玻璃窗的2个边长分别为a和b,厚度为t。在玻璃窗平面内建立平面直角坐标系Oxy。假设外界均布载荷q0的作用下在垂直于xy平面产生的挠度为w(x,y),利用简支矩形薄板的纳维叶(Navier)解法,挠度w(x,y)的表达式可以用下面的重三角级数表示[7]:
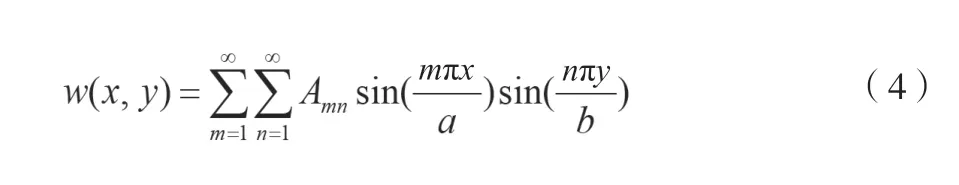
其中,m,n=1,3,5,7,…,取奇数。在均布载荷q0作用下,系数Amn如下。
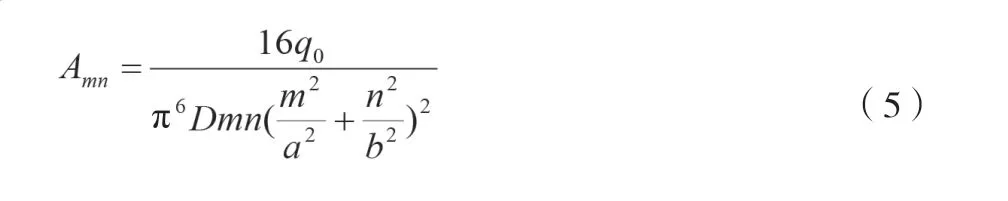
如图4所示,四边简支薄板中x横截面和y横截面上单位长度的剪切内力如下。

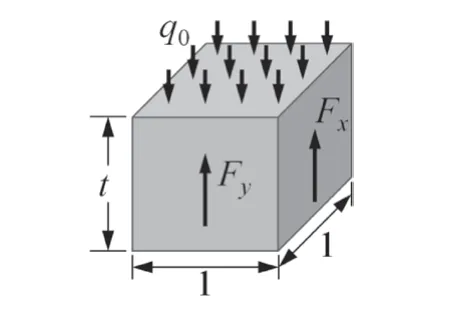
图4 厚度为t,长、宽均为单位长度1的微元六面体中剪切内力示意图

假设胶条在x=0、a2个边界上对车体的接触应力和接触长度分别为qa和δa,胶条在y=0、b2个边界上对车体的接触应力和接触长度分别为qb和δb,则不漏雨的条件如公式(8)所示。

一般情况下,在全胶条密封车窗结构的实际设计中,会使qa=qb,δa=δb。假设qa=qb=q,δa=δb=δ,则根据公式(8):
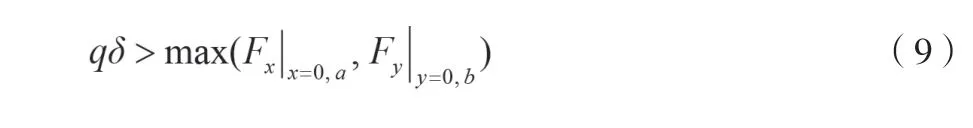
式(9)表明:胶条与车体的接触应力q和接触长度δ设计值的乘积要大于外载作用引起的胶条与车体接触面上单位长度附加力的最大值才能保证车窗不漏雨。
3 全胶条密封车窗胶条接触应力计算实例
为验证车窗受外部载荷作用下力学分析的正确性,该文采用有限元计算软件ANSYS对某轨道车辆车窗玻璃在外界均布载荷作用下的变形问题进行了数值模拟。车窗玻璃多采用多层中空结构,该文主要研究外载作用引起的胶条与车体密封力的变化,忽略中空结构,将车窗玻璃看成厚度t为6.2mm,长a、宽b均为990mm的单层钢化玻璃(该尺寸来源于中车四方芝加哥某项目的轨道车辆车窗尺寸)。由此,该文通过四边简支的矩形薄板来模拟车窗结构,得到铰支座处的约束反力数值结果,即外界载荷作用下,在胶条与车体接触面上产生的附加力,并与理论分析结果进行对比。材料参数包括[8-9]钢化玻璃密度ρ=2530kg/m3,弹性模量E=70GPa,泊松比μ=0.21。车体与胶条表面间的静摩擦系数γ为0.672。在模型周边施加简支约束,载荷条件为均布面载荷q0,以芝加哥一年中最大的风载荷945Pa作为载荷条件,即q0=945Pa。车窗玻璃有限元计算模型如图5所示,模型采用壳体单元,单元数为841,节点数为900。图6显示了数值模拟的变形云图结果。从图中可以看出,在外界均布载荷作用下玻璃窗的中心点处变形最大,四边简支的边界上没有变形,这与理论分析中边界上的挠度为0的结果相符合。

图5 车窗玻璃的有限元计算模型
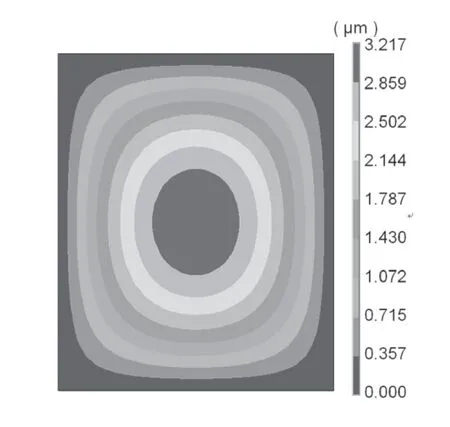
图6 车窗玻璃在外界均布载荷作用下的变形云图
由于车窗长a和宽b相等,由对称性可只研究一个边界上的作用力。该文考察随坐标y变化的结果。将车窗材料性能参数及尺寸参数代入式(6),便可求得外载引起的附加力随坐标y的变化。图7给出了理论分析与数值模拟的对比结果,两者符合很好,与已有研究结果变化规律相同[10],说明了理论分析结果的正确性。外部载荷q0作用在车窗上,在胶条与车体接触面上产生了附加力,从理论和仿真结果可以看出,该作用力大小沿边长呈抛物线形状变化,在车窗四边中心点处有最大值。理论分析得到单位长度的作用力最大值为306.19N/m, ANSYS模拟得到的该作用力的最大值为315.69N/m,两者误差为3.1%。由(11)式可知,胶条与车体的接触应力和接触长度设计值q和δ的乘积应满足,qδ>309.19 N/m。根据计算结果,在图8中给出了q和δ的乘积结果曲线和车窗在外载下不漏雨的设计区域。
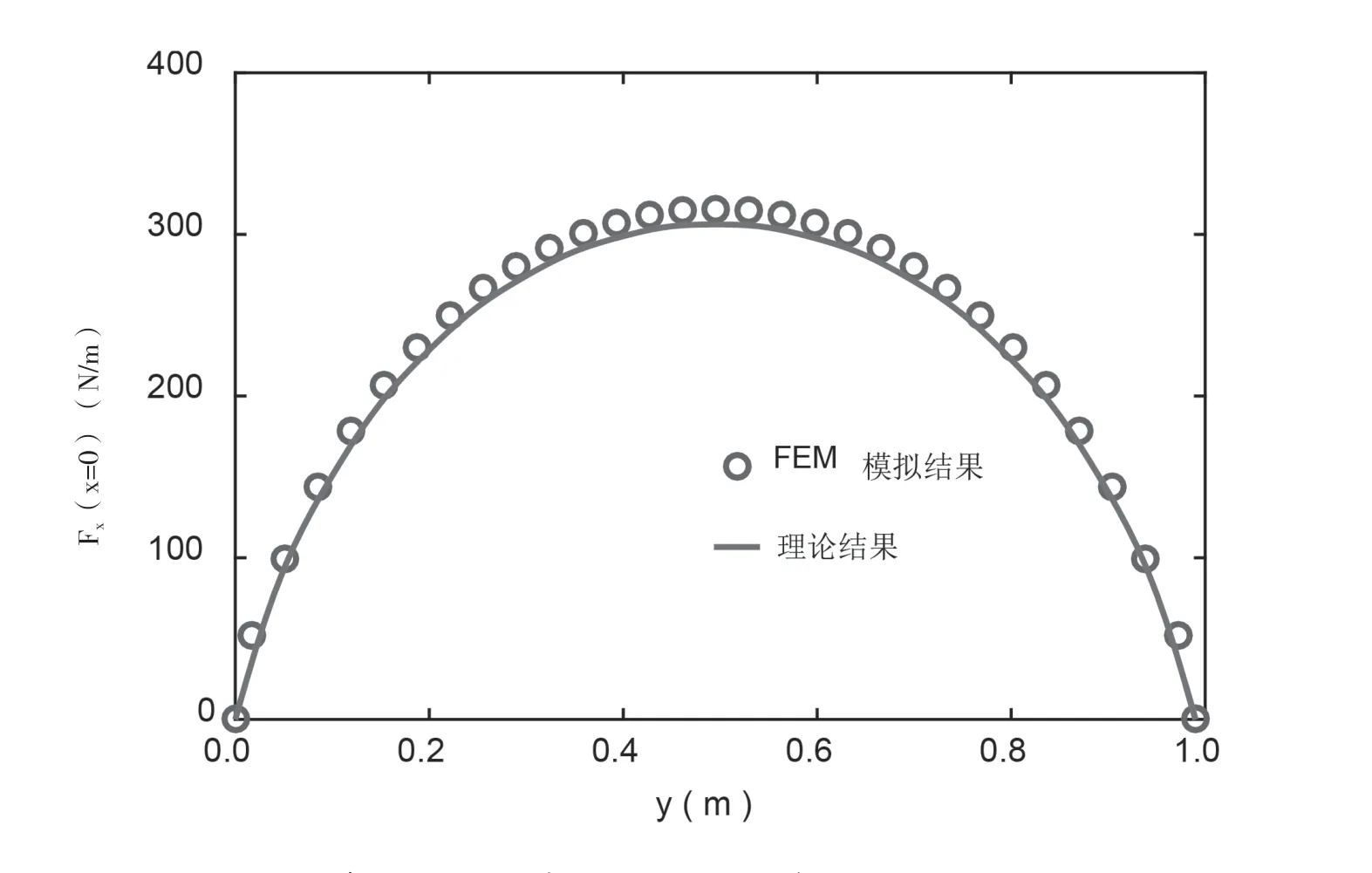
图7 单位长度附加力随窗框边长变化的理论分析和数值模拟结果对比
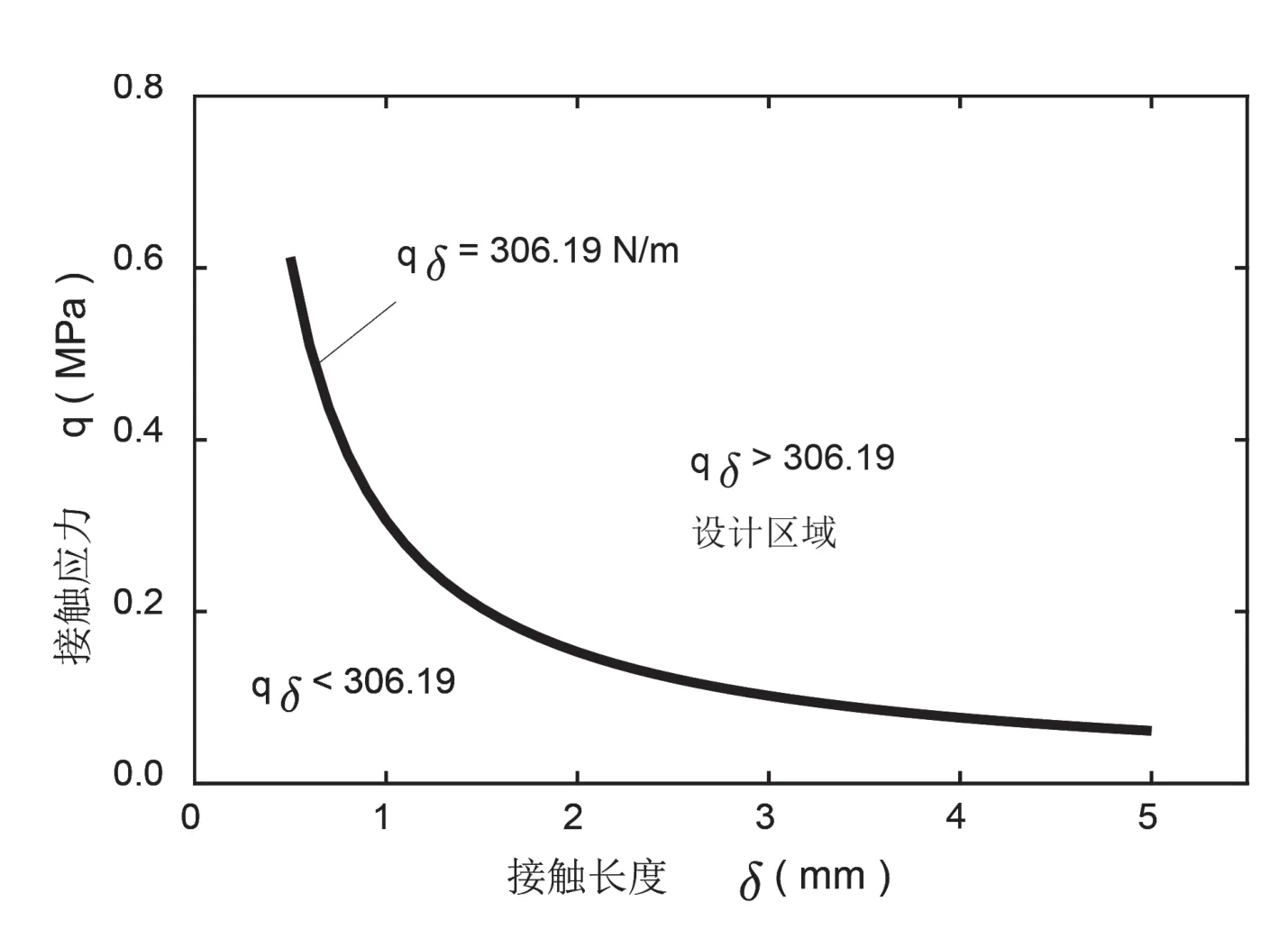
图8 胶条与车体接触面上的接触应力q和接触长度δ乘积结果
4 结语
该文以全胶条密封车窗结构为研究对象,首先对全胶条密封车窗漏雨情况进行了定性分析,只要胶条对车体的密封力设计初值始终大于外载引起的胶条与车体外侧接触面上的附加力最大值,车窗就不会漏雨。通过板壳力学理论分析了车窗玻璃受均布载荷的问题,得到了不漏雨条件下胶条与车体的接触应力与接触长度设计值应满足的关系式。将该文提出的方法应用到具体案例中,发现外部载荷作用于车窗玻璃引起的胶条与车体接触面上的附加力大小沿边长呈抛物线形状变化,车窗四边中心点处的作用力最大。利用ANSYS软件对车窗受外部载荷作用情况开展了有限元数值模拟,对比验证了理论分析方法的正确性。该文研究给出一种计算全胶条密封车窗接触应力和接触长度的方法,对全胶条密封车窗结构胶条尺寸的设计具有重要指导意义。

