抗浮锚杆的设计及受力性能分析

刘斌强

（甘肃省建筑设计研究院有限公司，甘肃 兰州 730031）

1 概述

随着城市建设用地供需矛盾的日益加剧，开发和利用地下建筑成为解决上述矛盾的有效方法。由于地下建筑的基础埋深较深，建设地点位于河岸边的此类建筑，大多数情况下，场地地下水位较高，此类建筑所受的水浮力较大，抗浮设计备受各方关注。

目前，建筑工程采用的抗浮设计方法有压重法，排水限压法、隔水控压法、泄水降压法，锚杆法，锚桩法［1］。由于抗浮锚杆布置间距小，布置密集，在水浮力较大时，基础底板受力均匀，施工速度快，造价低等，抗浮锚杆在建筑工程的抗浮设计中被大量采用。

本文通过初步的手算估算和有限元精确计算两种计算方法，对一地下三层的建筑的抗浮锚杆进行受力分析，对比了上述两种算法的差异，并计算分析了抗浮锚杆的抗拉刚度和基础底板厚度对其受力性能的影响，为实际工程的抗浮锚杆设计提供参考。

2 工程概况

如图1 所示是兰州地区黄河岸边某一地下三层的地下建筑，其中负三层和负二层为地下车库，负一层为超市。负三层和负二层的层高均为4.5m，负一层的层高为5.1m，负一层顶板覆土厚度为1.8m，柱网尺寸为8.4mx8.4m。负三、二、一层地下室外墙厚度分别为450mm、400mm、300mm；框架柱截面尺寸为600x600mm；负三层和负二层的结构布置为主框架梁+十字次梁，其中主框架梁截面为300mm×800mm，次梁截面为250mm×600mm，板厚为120mm；负一层结构布置为主框架梁+大板，其中主框架梁截面为500mm×1100mm，板厚为300mm。基础采用平板式筏型基础+下柱墩，筏板厚为800mm,下柱墩的尺寸根据柱冲切确定。地下室混凝土的强度等级为：墙、柱为C45，梁、板为C40。基础持力层为④卵石层，地质情况见表1，结构布置如图1 所示。

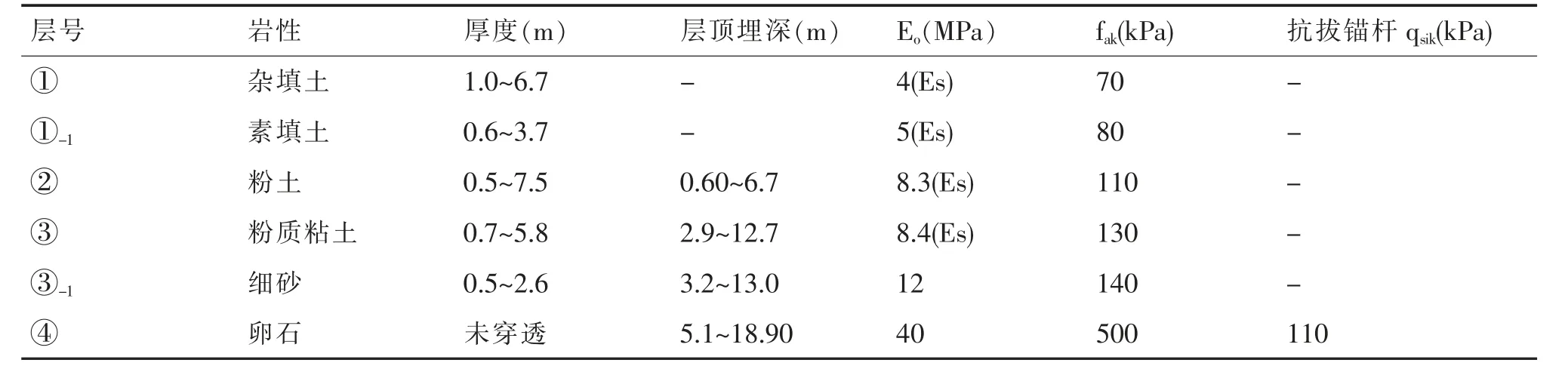
表1 土层物理力学指标

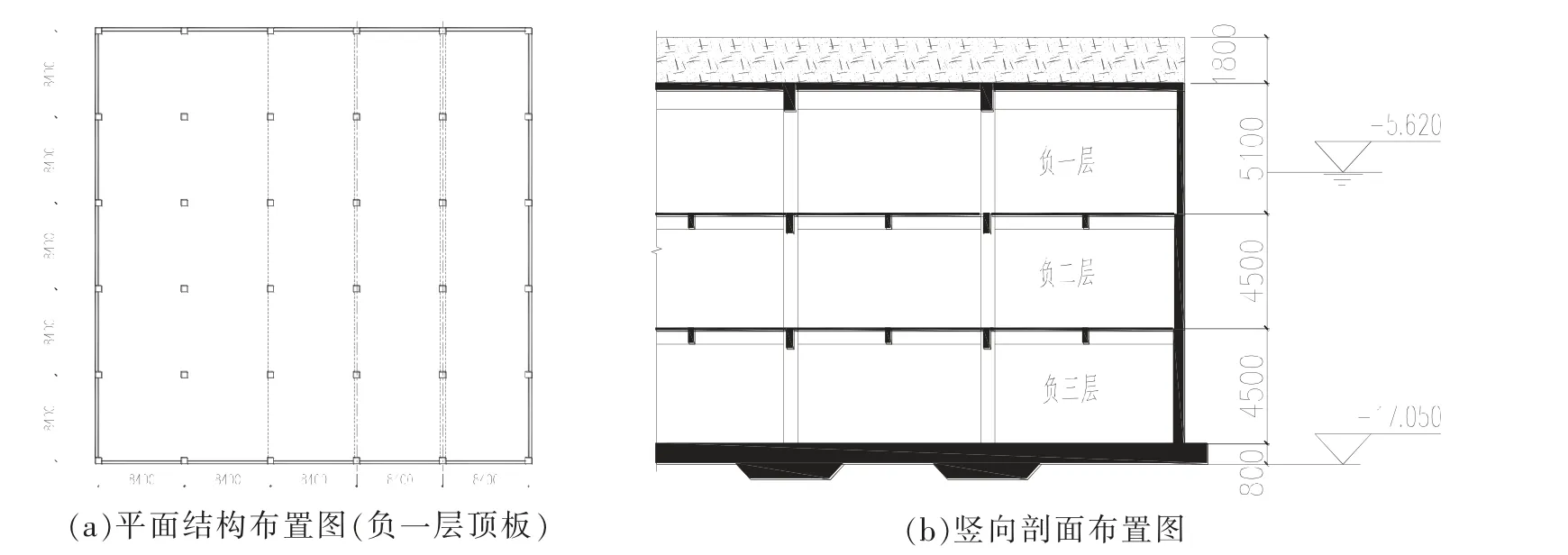
图1 结构布置示意图

3 基于手算的抗浮锚杆的设计

3.1 地下室抗浮验算

该建筑的各层自重及压重均采用盈建科建筑结构设计软件YJK-A（v2020-2.0.3）自动计算统计如下：

基础底板自重：Gk0=0.8×2.5=20kPa，

负三层自重：Gk1=10.7kPa

负二层的自重：Gk2=10.2kPa，

负一层的自重及压重为：

Gk3=15.0+1.8×18=40.4kPa

水浮力作用值为：

Nw，k=（17.050-5.620）×10=114.3kPa

建筑物自重及压重之和为：

Gk=Gk0+Gk1+Gk2

Gk3=20+10.7+10.2+47.4=88.3kPa

根据《建筑地基基础设计规范》［2］(GB500072011)5.4.3 条：

故抗浮稳定性验算不满足设计要求。

3.2 抗浮锚杆抗拔承载力特征值的初步估算

抗浮锚杆的直径拟采用150mm，长度为9m，根据岩土工程勘察报告，锚固体与土层见粘结强度标准值qsia=110kPa，根据 《建筑工程抗浮设计标准》（JGJ476-2019），公式（7.5.5-2）土层锚杆极限抗拔承载力标准值为：

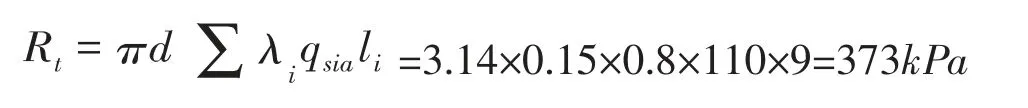
根据公式（7.5.7）条，抗拔锚杆承载力特征值

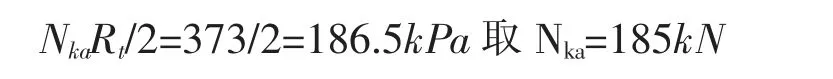
3.3 锚杆间距的初步估算

取基础底板的1m2为一个计算单元，则1m2抗浮所需的抗拔力为：

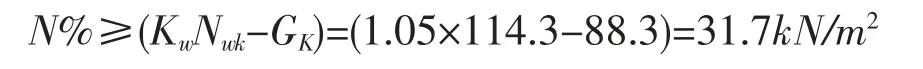
则锚杆间距为：

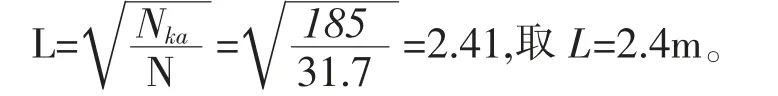
抗浮锚杆的局部布置如图2 所示：

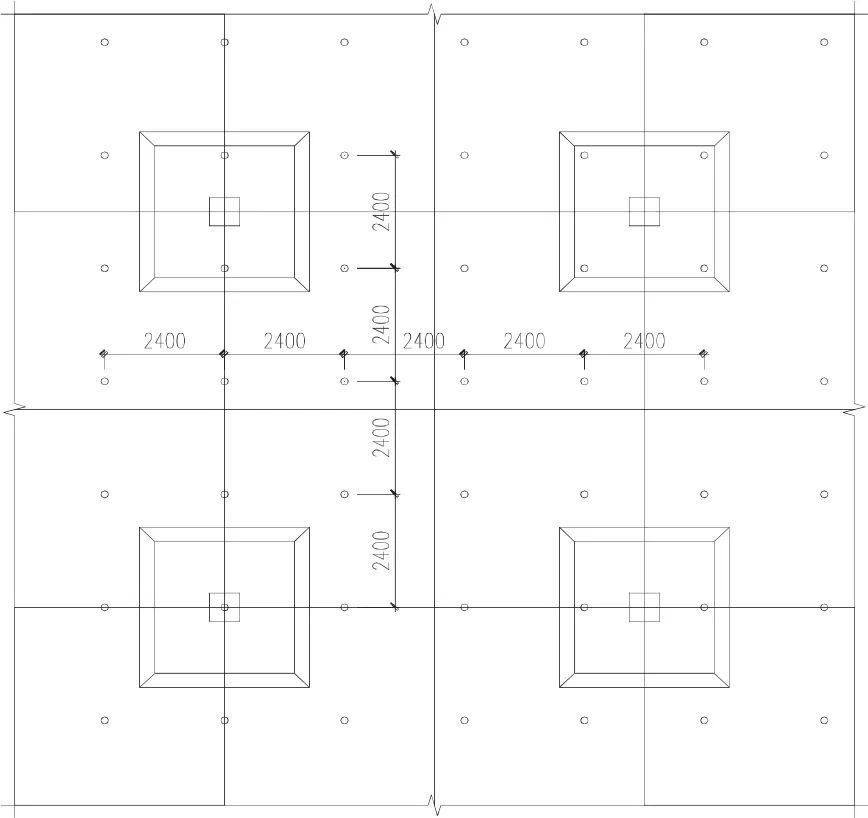
图2 锚杆平面布置图（局部）

3.4 锚杆筋体截面面积的计算

锚杆筋体钢筋选用预应力螺纹钢筋（fptk=1080kPa），根据《建筑工程抗浮设计标准》（JGJ476-2019）公式（7.5.6）：

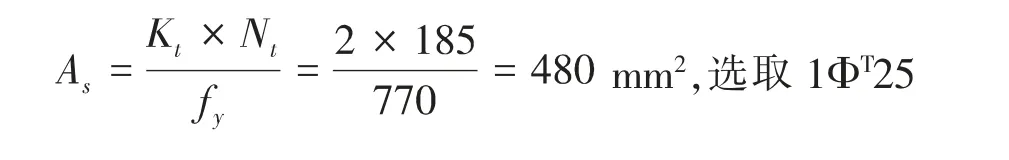
4 基于有限元的抗浮锚杆拉力计算

工程采用盈建科基础设计软件YJK-F（V2020-2.0.3），对抗浮锚杆进行有限元分析计算。建筑的各层自重及压重、抗浮锚杆布置及抗拔承载力特征值均与手算的情况相同。模拟抗浮锚杆时，抗压刚度取0，抗拉刚度K 取承载力设计值/允许位移（10mm）的比值，即经有限元计算分析，在1.0 恒-1.0 浮工况下，基础底板的三维位移如图3 所示。现从左到右依次选取横向各抗浮锚杆并定位，如图4 所示，依次统计这些抗浮锚杆的内力，如图5 所示。

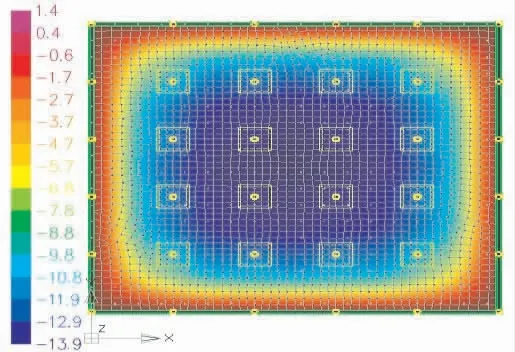
图3 基础底板的位移图（局部）（负值为向上）

图4 分析所选取的抗浮锚杆平面定位图

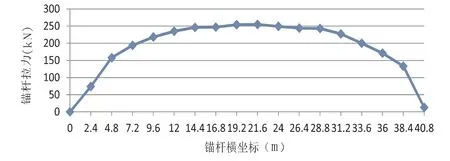
图5 不同位置抗浮锚杆拉力图

图3 的计算结果表明：在考虑上部结构刚度的情况下，基础底板在自重和水浮力的共同作用下，存在竖向位移，边跨的竖向位移较小，越往中间跨区域，竖向位移越大，中间区域，竖向位移达到最大，这与不考虑基础底板竖向位移的假定差别较大。究其原因，对整个结构而言，周边的地下室外墙在竖向相当于高深梁，刚度很大，故地下室外墙附近周边区域的基础底板竖向位移小，而中间跨区域由于没有外墙竖向的约束而竖向刚度相对较小，故基础底板在中间跨区域竖向位移较大。

图5 的计算结果表明，在地下室外墙附近周边区域的锚杆拉力较小，越往中间跨区域，锚杆拉力越大，在基础底板的中间区域，锚杆拉力达到最大，究其原因，锚杆的拉力与基础底板的竖向位移存在线性正比关系。其中拉力超过抗拔锚杆承载力特征值Nka=185kN 的锚杆数量占总锚杆数量的66%。传统的以手算为主的抗浮锚杆设计方法无法考虑上部结构竖向刚度，假定为地基底板为刚性板，没有竖向位移，故认为抗浮锚杆的受力都是均匀的，这种设计方法存在严重的安全隐患。

5 锚杆的抗拉刚度和底板的厚度对锚杆拉力的影响

5.1 锚杆抗拉刚度的影响

现分别选取锚杆的抗拉刚度K1=18500/2=9250kN/mm,K2=18500kN/m,K3=18500×2=37000kN/m，在1.0 恒-1.0 浮工况下，选取图4 所示锚杆的计算拉力，如下图6 所示。为了分析所选锚杆的整体拉力水平，用样本平均值［3］衡量锚杆拉力的平均拉力水平：

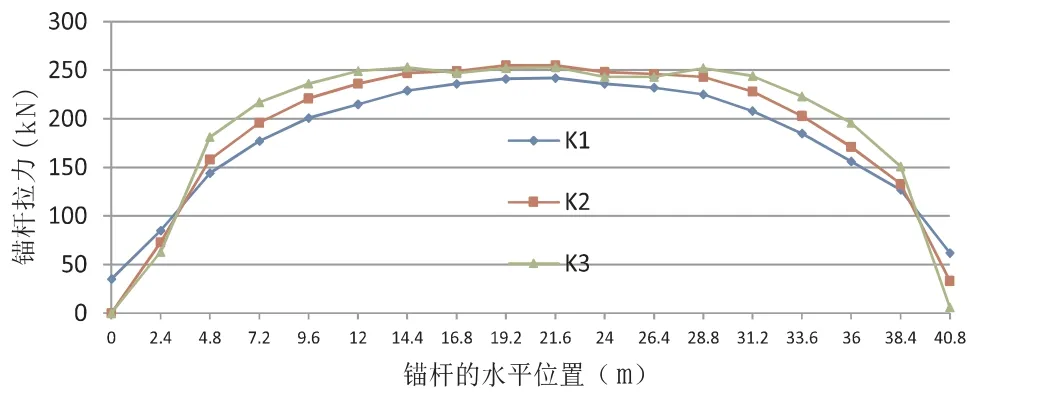
图6 不同抗拉刚度下抗浮锚杆拉力分布图

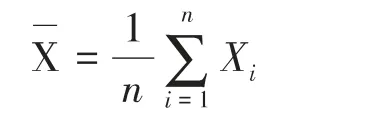
式中ni为所选锚杆的数量，Xi为所选锚杆的每个锚杆的拉力,用样本标准差表示锚杆拉力与样本平均值得偏离程度：

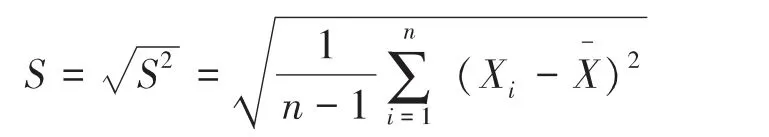
在不同抗拉刚度下，锚杆拉力的均值如图7 所示，标准差如图8 所示。

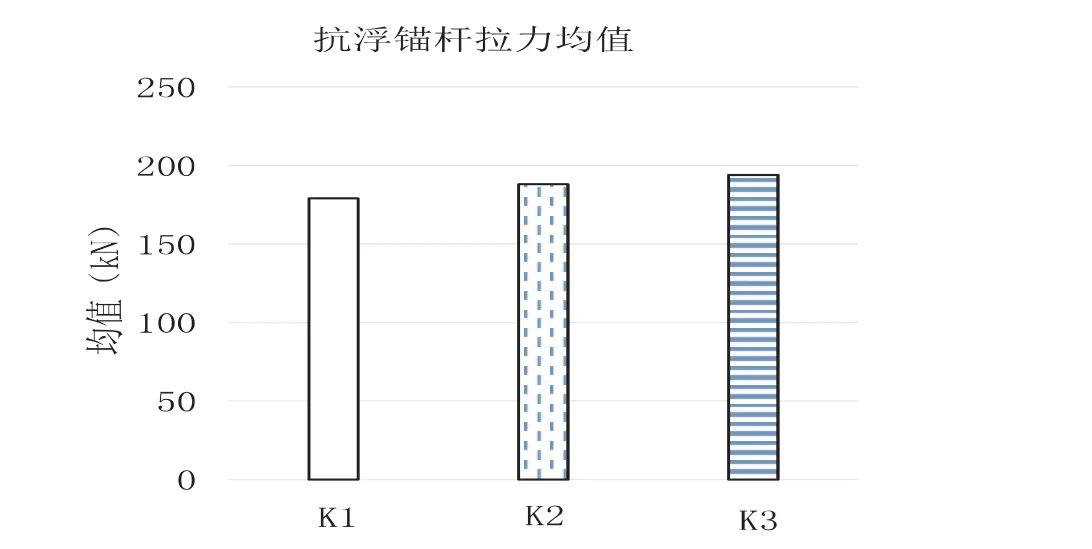
图7 不同抗拉刚度下抗浮锚杆拉力均值

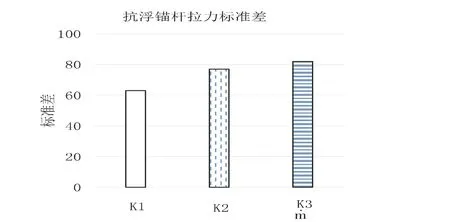
图8 不同抗拉刚度下抗浮锚杆拉力标准差

计算结果表明：随着抗浮锚杆的抗拉刚度越大，锚杆拉力的样本平均值越大，说明锚杆拉力的整体平均拉力越大；同时，锚杆拉力的样本标准差也越大，说明锚杆拉力的不均匀性越严重。

5.2 底板厚度的影响

现分别取基础底板厚度h1=600mm，h2=800mm，h3=1000mm，在1.0 恒-1.0 浮工况下，选取如图4 所示部分从左到右的一排锚杆的计算拉力，如图9 所示。

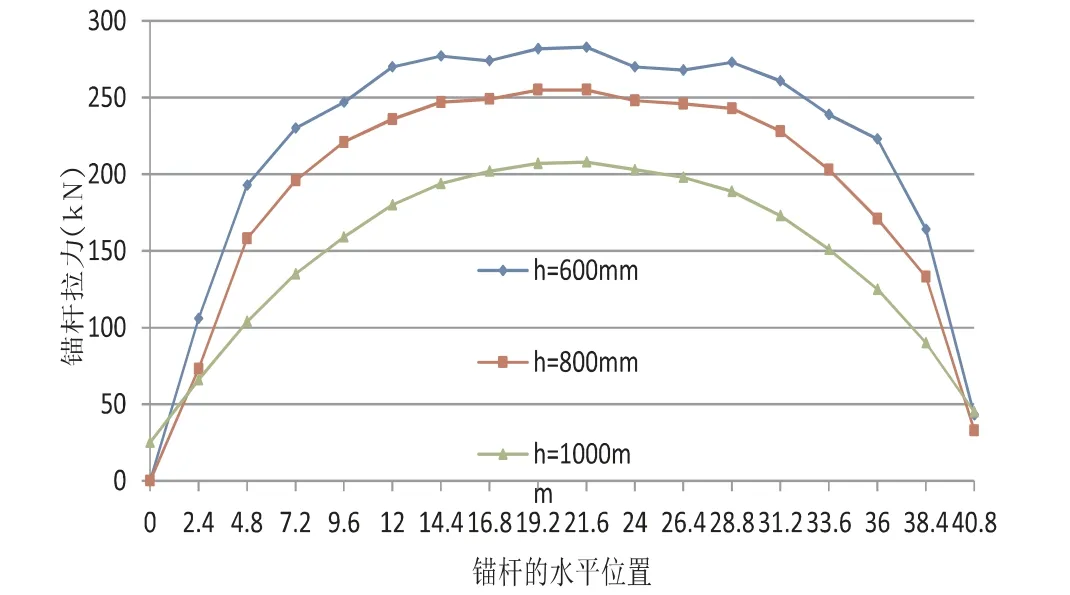
图9 不同筏板厚度下抗浮锚杆拉力分布图

为了分析锚杆的整体拉力水平，用本文5.1 节所表述的样本平均值表示锚杆拉力的平均拉力水平，用样本标准差表示锚杆拉力与样本平均值得偏离程度，在不同抗拉刚度下，锚杆拉力的均值如图10 所示，标准差如图11 所示：

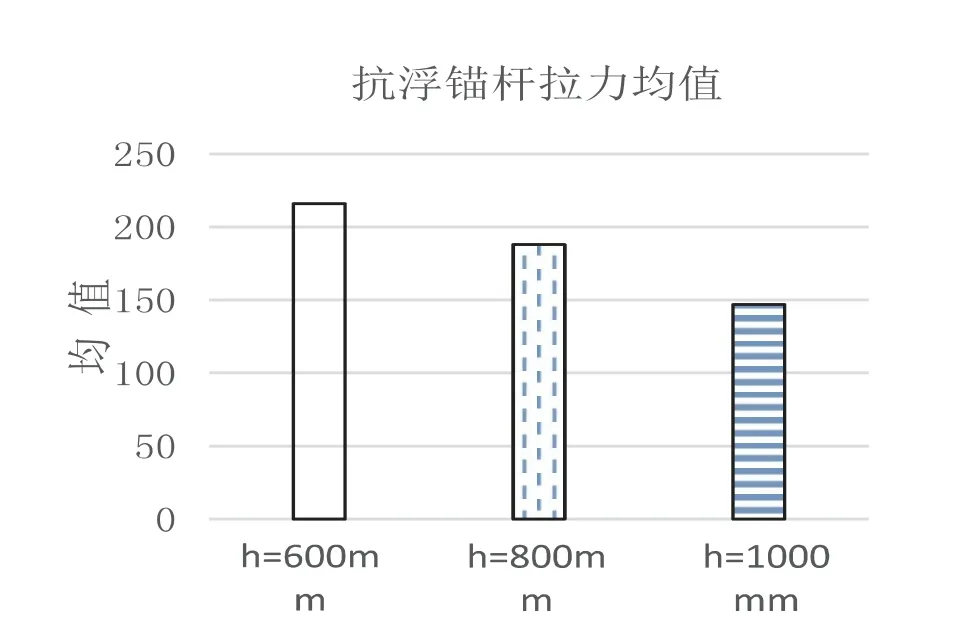
图10 不同基础底板厚度下抗浮锚杆拉力均值

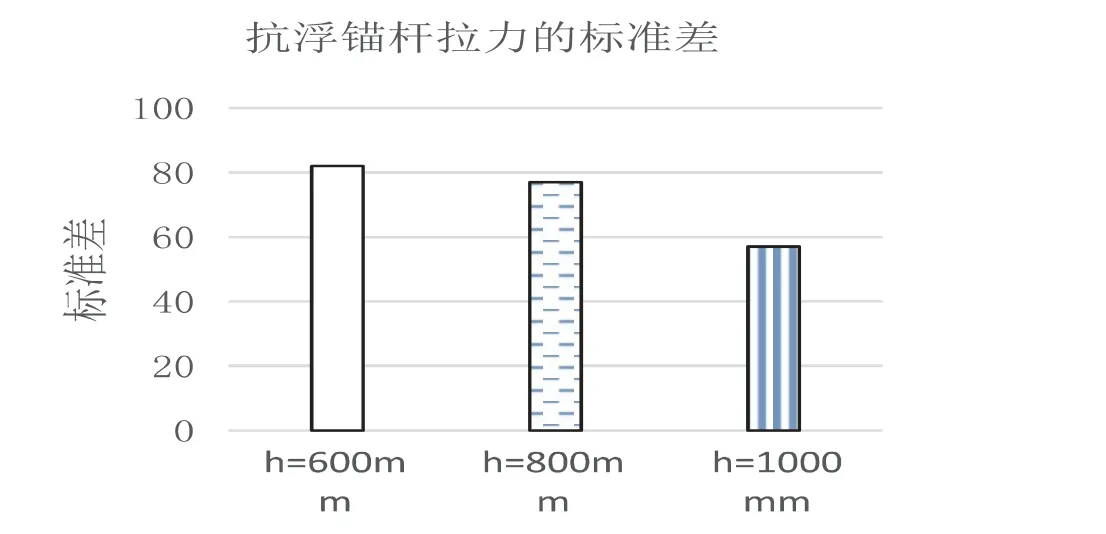
图11 不同筏板厚度下抗浮锚杆拉力标准差

计算结果表明：随着筏板厚度的增加，锚杆拉力的样本平均值越小，说明锚杆拉力的整体平均拉力越小；同时，锚杆拉力的样本标准差也越小，说明锚杆拉力越均匀。

6 结论

本研究通过对一地下结构分别进行简单手算的抗浮锚杆设计和有限元模拟计算分析，得出结论如下：

（1）有限元分析计算表明，在1.0 恒-1.0 浮工况下，锚杆的拉力不是均匀的，以每个锚杆的拉力都是均匀的为前提的传统的手算设计抗浮锚杆的方法存在安全隐患。抗浮锚杆地设计应采用以简单手算和有限元的精确计算相结合的方法。

（2）抗浮锚杆的抗拉刚度对抗浮锚杆的整体拉力水平和拉力的离散型有影响，抗拔刚度越大，抗浮锚杆整体拉力水平越大，拉力的离散型也越大。因此，在设计抗浮锚杆时，抗拉刚度应适当减小。

（3）基础底板的厚度对抗浮锚杆的整体拉力水平和拉力的离散型也有影响，筏板厚度越大，抗浮锚杆整体拉力水平越小，拉力的离散型也越小。因此，当筏板下设置抗浮锚杆时，筏板厚度应适当加大。