分布式垂直轴风力发电机的并网特性分析

李争，董皓，曹欣，张文达，于絮泽，孙鹤旭

（1.河北科技大学 电气工程学院，河北 石家庄 050018；2.河北建投新能源有限公司，河北 石家庄 050051）

风能已成为全球可再生能源研究的重点，许多国家将风能作为其与环境有关的长期计划的基础[1-2]。风能利用效率的高低主要取决于风力涡轮机的类型。风力涡轮机有两种类型：水平轴以及垂直轴风力涡轮机。经过数十年的垂直轴风力涡轮机研究，发电技术被认为是成熟的，已广泛应用于大型发电厂。近年来，随着技术的进步以及风力发电的广泛普及，垂直轴风力涡轮机受到的重视程度日益增加，已成为许多学者的研究对象。垂直轴风力涡轮机由于其自身的优势，在补充能源、能源行业的结构调整以及在低风速地区捕获风能方面发挥着重要作用[3]。随着计算流体动力学的发展日益成熟，已经证明垂直轴风力涡轮机在流体动力学方面，有非常优异的性能，并且在风能利用率以及造价成本上，相比于其他风力机都有独特的适应性，研究探讨垂直轴风机的性能以及应用技术显得尤为必要。随着研究的不断深入，发现这种风机类型是最有前景的中小型风机[4-5]。但是关于垂直轴风机并网的研究还较为鲜见。综上，本文对一种新型鹦鹉螺等角螺线型垂直轴风力机进行了研究，对该类垂直轴风机并网的可行性做出验证，并进行了仿真研究，通过仿真实验数据分析风机在并网发电中的运行情况。

目前，大多数研究人员分析垂直轴风力机的空气动力性能的方法为数值模拟方法。文献[6]分析研究了垂直轴风力机的特性，并将其特性与水平轴风力机的特性进行了比较，强调了两种风力机各自的优缺点。在文献[7]中，提出了一种新型的双转子风力涡轮机，并通过数值模拟分析了空气边界层对风力涡轮机气动性能的影响。基于升力线模拟方法，完成了MW级风力发电机的设计，并在设计过程中考虑了空气动力学因素。研究了不同垂直轴风力发电机对空气动力性能的影响[8]。文献[6-8]通过数值模拟方法对风力涡轮机的空气动力性能进行了深入分析，但是这些分析仅完成了风力机性能参数的基本研究，未能给出提高其性能的方案。综上所述，采用数值模拟作为本文的主要分析方法。

随着风力发电普及性的提高，对于风电机组容量的提升需求也更为迫切，采用增速齿轮箱的双馈变速风电机组的成本上升，且故障率较高，在对于风力发电机组可靠性要求提升的情况下，垂直轴风机更为受到重视，文献[9]在PSS/E中建立了转速为恒定的风电机组，根据永磁同步电机的风电机组动态模型，文献[10]分析了双PWM永磁同步风电机组对于机侧变流器的控制方案，并且对于发电机侧端电压的控制提出了增加约束方程的方案，文献[11]介绍了风力发电并网的要求及其控制原理，文献[12]介绍了可变步长的最大功率跟踪算法。

本文在已有技术基础上，采用有限元仿真软件，构建了3D风力发电机模型。分析了诸如风能利用率和转矩等基本参数，然后建立发电机的数学模型，并分析其发电特性，验证了鹦鹉螺等距螺旋风力发电机在发电系统中的有效性和可行性。

1 风力机模型设计

1.1 风机基本参数的分析

根据牛顿第二定律，设F为力，m为质量，a为加速度，可得出结论力等于质量与加速度的乘积：

得出动能为

上述等式均在质量m为恒定值时有效，但由于风的质量是每时每刻都会发生变化的量，在不同时刻具有不同的速度。因此风的动力方程为

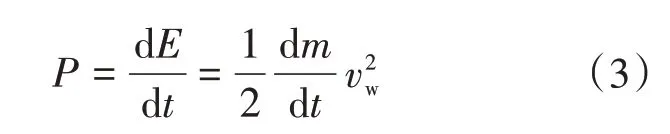
又因为

最终得到的公式为

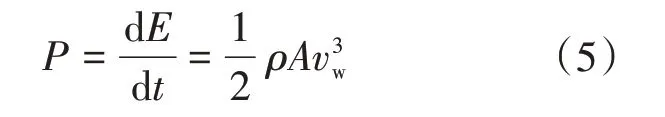
式中：vw为进入风速和出口风速的平均值；ρ为空气密度；A为风力机每个叶片实际扫风面积。

用平均风速vw代替公式（2）中的v，即可得在风力机的转子叶片中的机械动力为

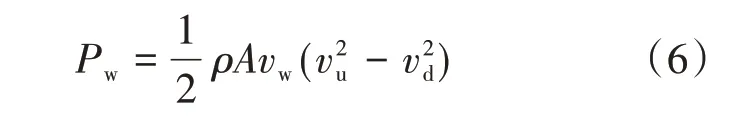
式中：vu为转子叶片入口处上游风速；vd为转子叶片出口处的下游风速。

但质量流率为

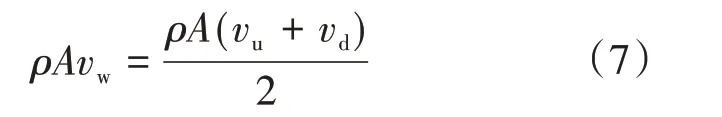
因此式（6）可以表述为

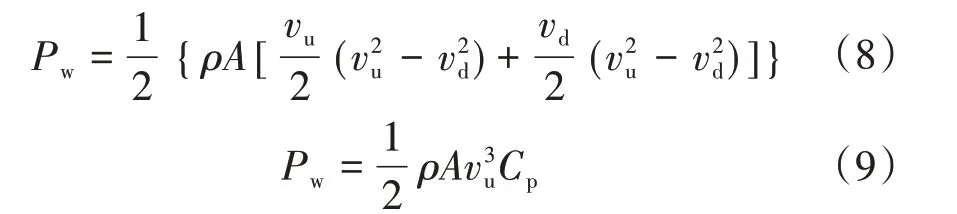
其中

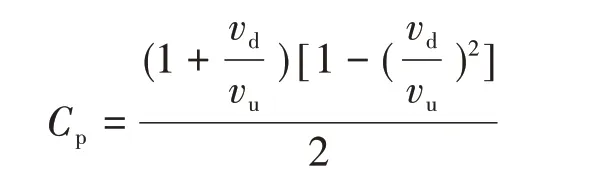
式中：Cp为功率系数。

式（9）为转子叶片在风中提取的机械动力的简化方程。

叶尖速比可以用vu和vd表示：

式中：R为风叶半径；ω为风叶旋转角速度。

转矩系数Ct的公式为

式中：D为风轮半径。

1.2 风机的基本结构

鹦鹉螺等距螺旋风力发电机由鹦鹉螺等距螺旋风力发电机、联轴器、增速箱、发电机、轴承、钢制支架、垂直轴、控制器、轴承座、电池、逆变器装置等组成。风轮由轮毂和鹦鹉螺等距螺旋叶片组成，图1a为鹦鹉螺等角螺旋风力机整体模型图。叶片的径向截面为椭圆形或对称翼型或对称等距螺旋形，图1b为叶片模型图。当叶片背向风时，其径向截面为椭圆形，此时，正好有一个椭圆形的叶片或对称的机翼或对称的等距螺旋，因此阻力系数很小。侧面正好面对风，阻力系数非常大，因此推力很高。同时，下风叶片延伸到上风叶片内部的部分也起着加速引导的作用。将来，当风被吸入迎风叶片的外部时，它将推动风轮以较小的力旋转。另一个特点是叶片是鹦鹉螺等角度螺旋形，旋转时的摩擦阻力很小，因此风轮转速很高。

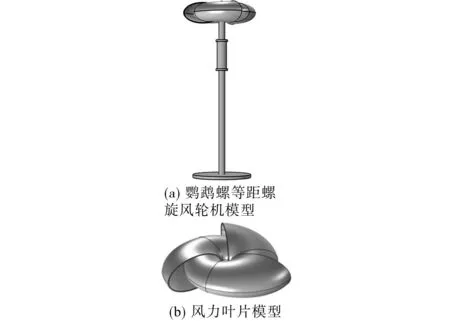
图1 新型鹦鹉螺等角螺线型垂直轴风力机结构Fig.1 Novel nautilus isometric helical vertical axis wind turbine structure

1.3 边界条件及其求解设定

为了模拟风力涡轮机在实际工作中的运行，ANSYS Workbench中的Fluent（CFX）模块用于流场分析[12]，该模块主要检查叶片的流固耦合以及风力涡轮机3D模型的空气动力学发展。发电机集成在驱动轴中。

图2为使用ANSYS CFX软件模拟的风力涡轮机流场的示意图。如图2所示，流场由两部分组成：固定区域和旋转区域。固定域是风力涡轮机所在的外部环境，旋转域是风力涡轮机叶片在其中工作的工作环境。为了模拟风力涡轮机真实环境，固定域的面积应比风力涡轮机的尺寸大得多，而旋转域的面积应比叶片旋转的面积略大。

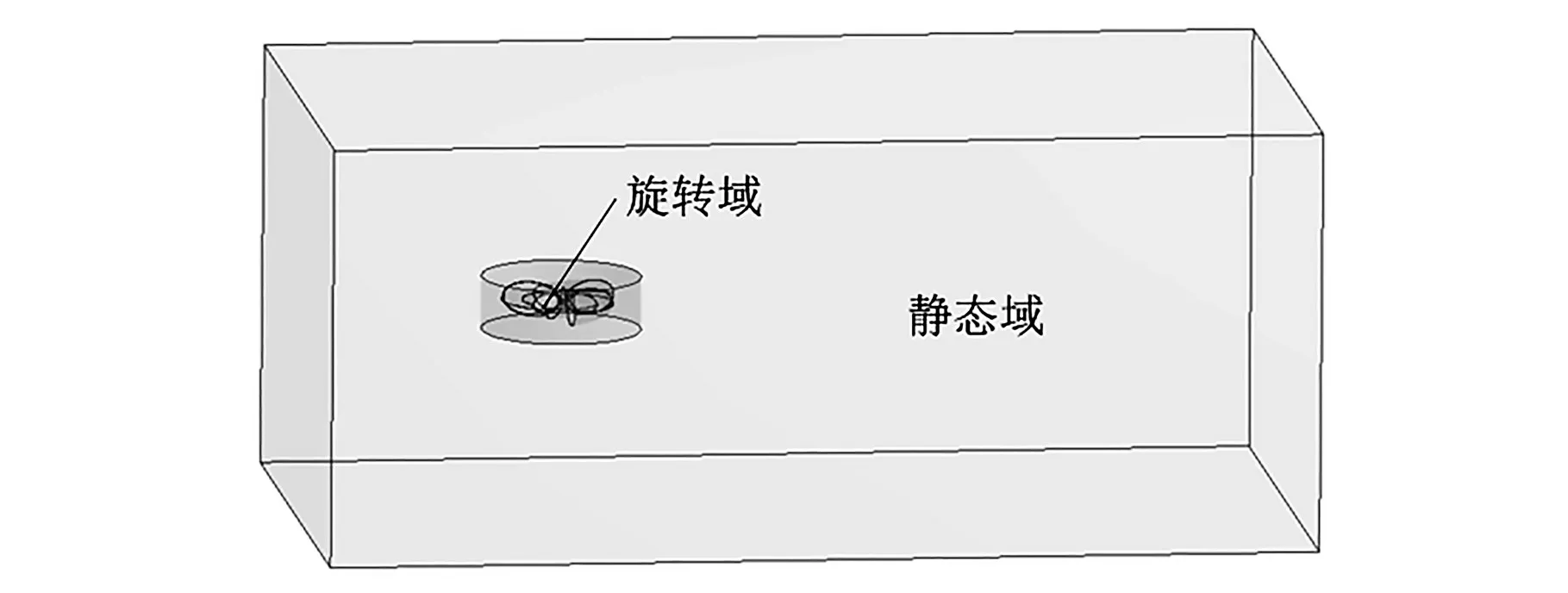
图2 风力涡轮机的静态域和旋转域Fig.2 Thestatic domain and rotating domain of the wind turbines

创建模型和流场后，需要进行网格划分，图3为网格划分示意图。

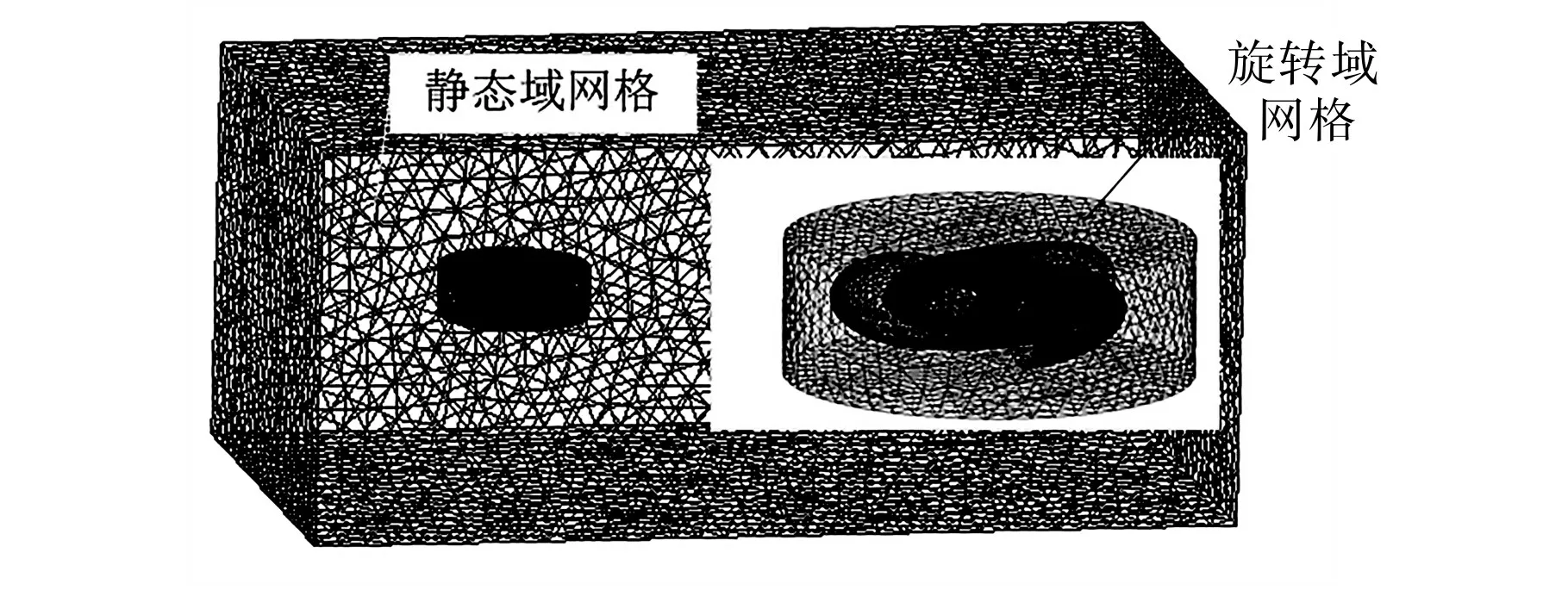
图3 网格划分示意图Fig.3 Schematic diagram of meshing

在划分过程中，选择的网格类型，网格布局和算法直接影响数值模拟结果的准确性[13]。本文使用自动网格划分方法，即经典划分方法。对于某些不规则模型，该划分方法通常能够满足计算要求。整个都是四面体网格，可以轻松地适应复杂的几何形状，该网格在模型的不规则点处相对密集，从而提高了计算精度。

在网格划分完成的基础上，ANSYS CFX软件求解器的设定也对最终结果的准确性有较大影响。在使用ANSYS CFX软件进行计算的过程中，主要使用的计算方程为雷诺平均N-S方程和可连续压缩方程。

图4为流体边界设置图。

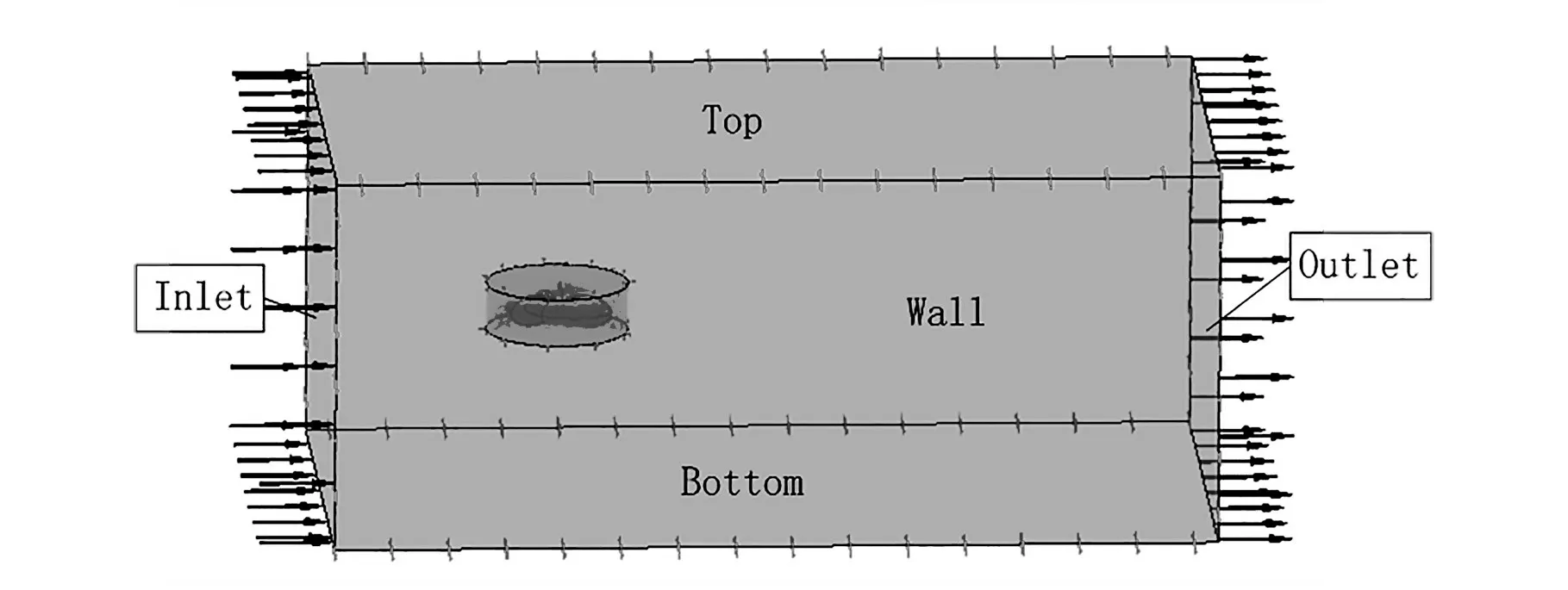
图4 流体域边界设置Fig.4 Fluid domain boundary setting

从图4中看出，流场主要分为旋转域以及静态域。静态域包括流动的气流以及风力机的支撑杆，模拟气流流入的方向和速度，考虑到后续的实验在内蒙古地区完成，设定入口为速度入口，风速设定1～10 m/s，中度湍流，出口为压力出口，压力设定0，静止域顶部和底部设置为墙，左右两侧设置为对称。旋转域包括风力机叶片、旋转轴以及风力机内部气流，模拟风力机叶片旋转的速度和方向，根据不同的叶尖速比（0.1～1），设定旋转场转动的角速度。为保证计算精度及计算的快速收敛，选用压力关联方程的半隐式方法（SIMPLE），该方法考虑了高阶解和逆风模式的共同作用，因此适用性好。具体模拟参数如下：雷诺数为6.0E+5，迭代步长为300，湍流模型为标准k-e模型，网格为100万，剩余指标为1.0E–4。除此之外，步长的选择十分关键，步长过长，计算时间延长，消耗大量时间；步长过短，会导致计算结果未收敛。经过大量计算验证，本文所用模型在步长达到300步时，达到计算精度。

2 分布模型联合仿真

采用ANSYS和Matlab仿真，ANSYS用来计算风轮转矩，得出的数据送入Matlab中进行仿真。具体步骤为：分别在Fluent和Simulink环境下建立各自的仿真模型，使用Fluent可得出发电机输出转矩，风轮转速，将得到的数据传递到Matlab仿真模型中，得到最终的并网数据。图5为风机模型在不同环境下仿真所得出的数据传递流程图。

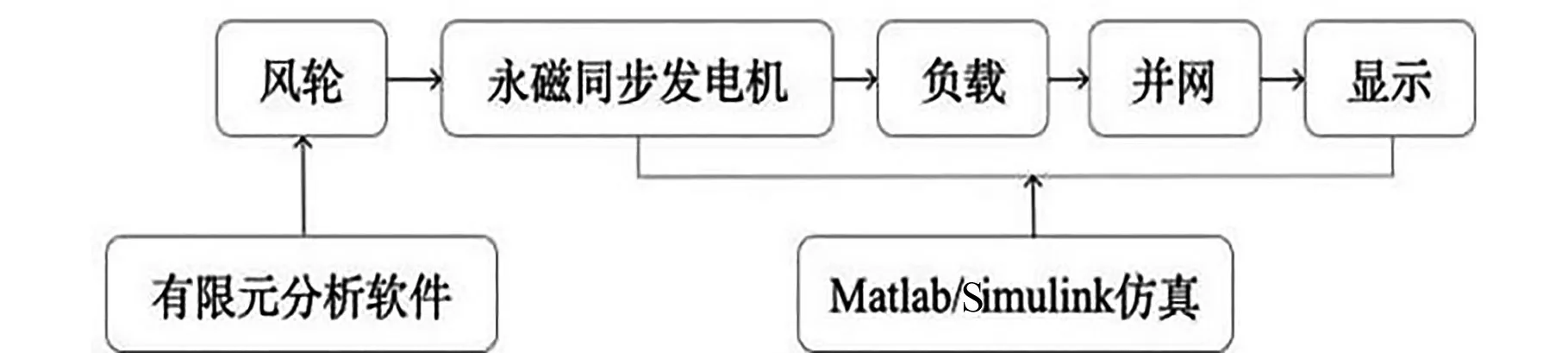
图5 仿真流程图Fig.5 Simulation flowchart

2.1 风力发电机模型

发电机转子的动态方程为[14-16]

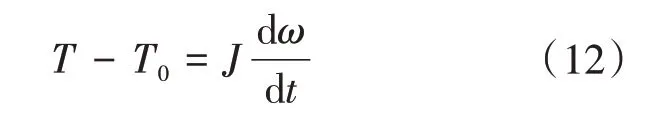
式中：T为风力机输出转矩；T0为阻力转矩；J为风力机转动惯量。

永磁同步发电机模型中，设定d，q轴方向：设定在永磁体转子中心线上为d轴，则其沿转子旋转方向超前90°为q轴，可得出d，q轴的数学模型。

电压方程为

式中：Rs为定子绕组每相电阻；usd，usq分别为电机端电压d，q轴分量；Ψsd，Ψsq分别为定子磁链d，q轴分量；isd，isq分别为定子电流d，q轴分量；ωe为电角速度。

电磁链转矩方程为

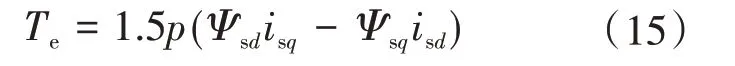
式中：p为发电机转子极对数。

2.2 系统结构

根据同步风力发电机组的并网原理、空气动力学原理、机侧变流器及网侧变流器控制原理搭建仿真模型结构，得到发电系统仿真模型如图6所示。

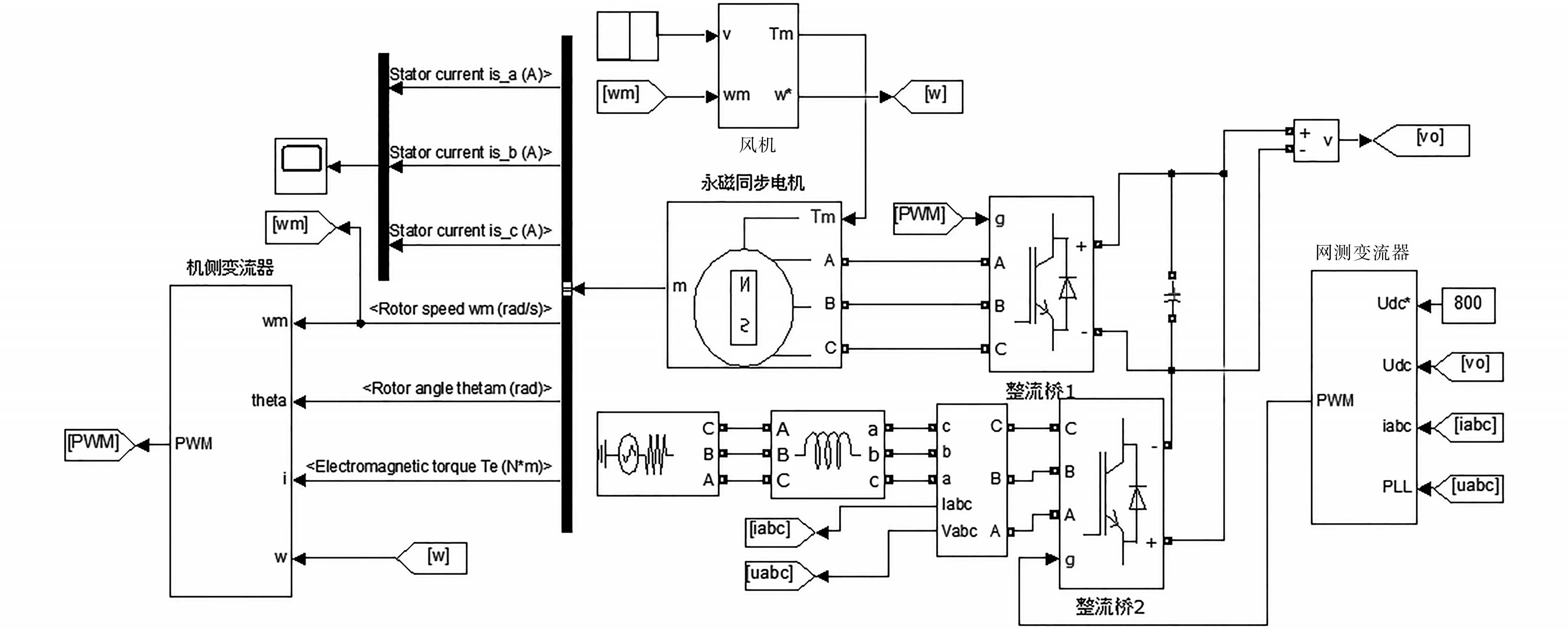
图6 发电系统仿真模型Fig.6 Power system simulation model

由ANSYS得到的风速等数据传递到Matlab模型中，将发电机输出的转速，电流及相位角送入变流器中，经过整流电路得到高压直流输出，又经整流电路降压还原为三相交流电进行并网，电网的电流、电压以及高压直流电送入网侧变流器。

2.3 控制策略

由于风速的不确定性以及不稳定性，在风力机中加入改变步长算法MPPT，随着风速的突变，MPPT算法的步长也随之发生改变，使风能利用率得到了提高。

发电机侧变流器的内部结构如图7所示。

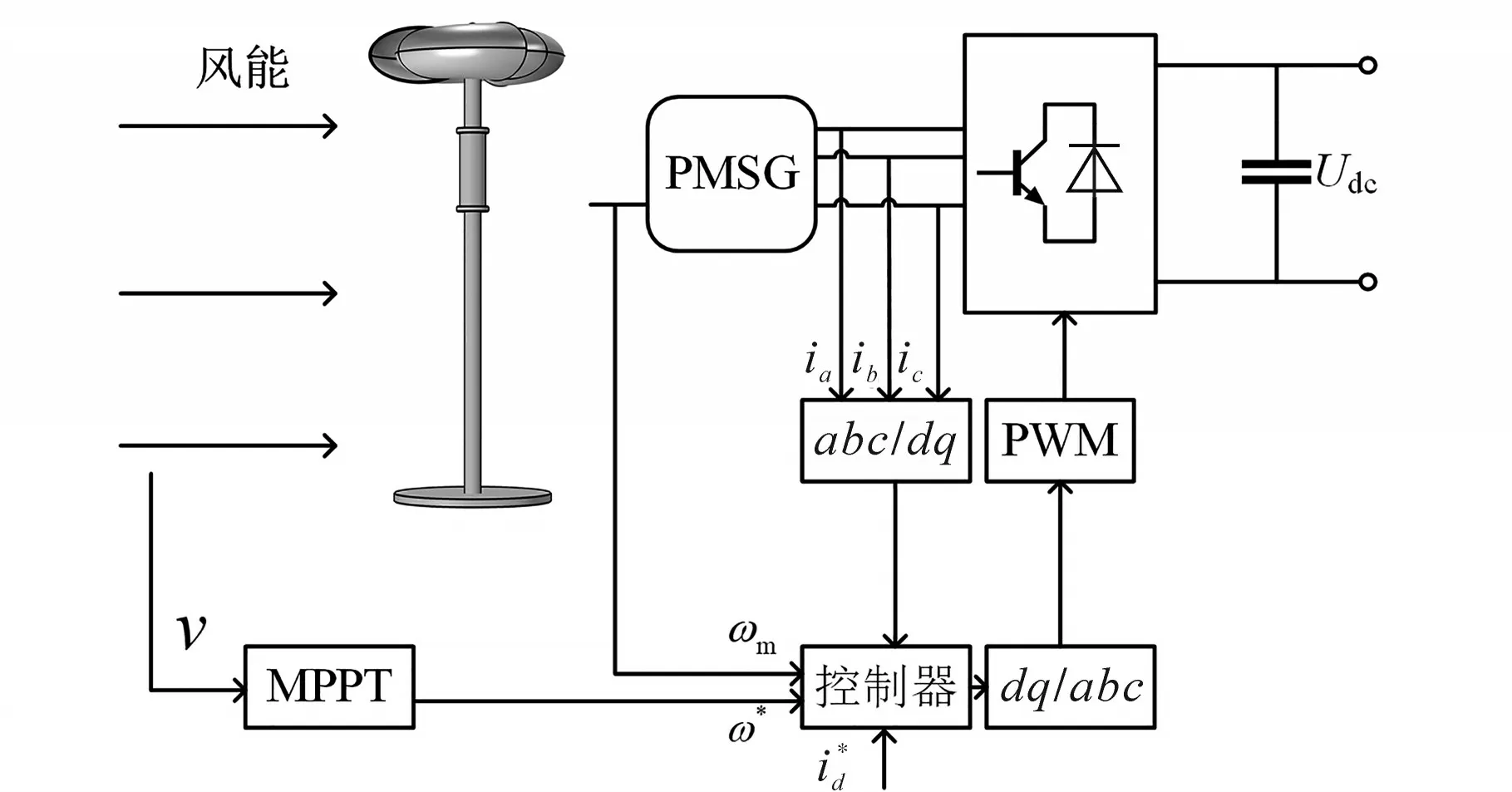
图7 机侧变流器内部结构Fig.7 Internal structure of generator-side converter

控制方法为：使PMSG送入变流器的有功功率按照最大功率曲线变化，可以最大限度的使能量得到利用，机侧变流器内部可以分为两个部分，内环控制器和外环控制器。

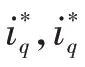
在可变步长的MPPT算法中，令R(k)为第k个寻优周期，根据寻优周期的不同状态可分为四种模式：当R(k)＞0且R(k-1)＞0时，系统功率处于上升阶段，则算法的步长应处于增加状态，以提高功率跟踪的速率；当R(k)＜0且R(k-1)＜0时，此时功率处于下降阶段，算法的步长处于减小状态；当R(k)＜0且R(k-1)＞0时，系统功率达到了顶峰并且开始下降，此时需要对步长进行指数衰减，使步长快速达到最大功率点的数值；当R(k)＞0且R(k-1)＜0时，需要衰减步长。令：

式中：Δiqs为算法中被扰动的步长数值；C为步长衰减系数[17]，取C=0.382。

当系统寻优周期处于R(k)R(k-1)＜0时，衰减步长皆为0.382Δiqs，当步长衰减n次后，则有：

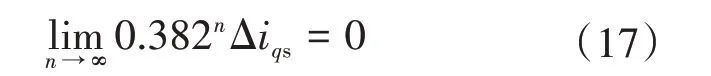
由式（17）可得，系统最终步长会收敛于0，在最大功率点附近处于微小震荡的状态，很大程度增长了系统的精确度。

电网侧变流器采用定子电压矢量控制方案，使电网侧变流器与电网之间实现了解耦控制，传输的有功功率与无功功率实现解耦，使电网电压位于d轴，即Ugq=0，实现解耦后电网输出的有功功率Pg和无功功率Qg为

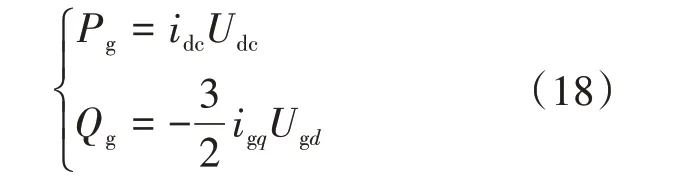
由式（18）可得，采用矢量控制后，无功功率和有功功率都变成了可单独进行控制的量。由此设计出的网侧变流器的内部结构如图8所示。

图8 网侧变流器内部结构Fig.8 Internal structure of grid-side converter

由图8可知，网侧变流器的主要构成为电压外环和电流内环，电压外环控制高压直流电，使用U*dc与Udc处理后经过PI控制进行调节计算，可得到d轴的电压分量。

设置q轴的电流分量的结果值为0，使期望的目标值与q轴电流分量相减得到误差信号，对误差信号进行PI控制进行调节计算，得到的结果为q轴的电压分量。得到的信号送入PWM模块，作为网侧变流器的驱动信号。

3 仿真结果分析

3.1 流场分析

图9为网格无关性验证曲线，其存在意义为在保证计算结果准确性的情况下，通过图像选择合适的网格数以达到节省计算时间，并且找到最佳网格划分数的目的。如图9可知，在网格数达到100万之后，网格数量对风力机转矩不再产生较大影响，因此选择网格数为100万作为后续计算基础，进行后续的性能分析。

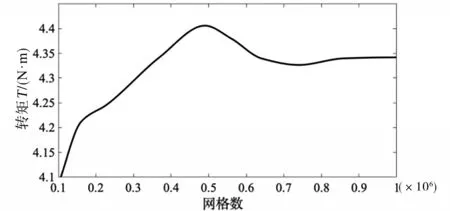
图9 网络独立性验证曲线Fig.9 Network independence verification curve

图10为叶尖速比—风能利用率曲线，图10中设定的叶尖速比的范围是0.1～0.7。风能利用系数随着叶尖速比的变化呈现的变化规律为先增大后减小，当叶尖速比TSR=0.4时，风能利用系数Cp达到最大值，此时的风能利用率为最高。可以达到最大程度地利用风能的目标，可以通过将风机速度稳定在一定数值内来实现。

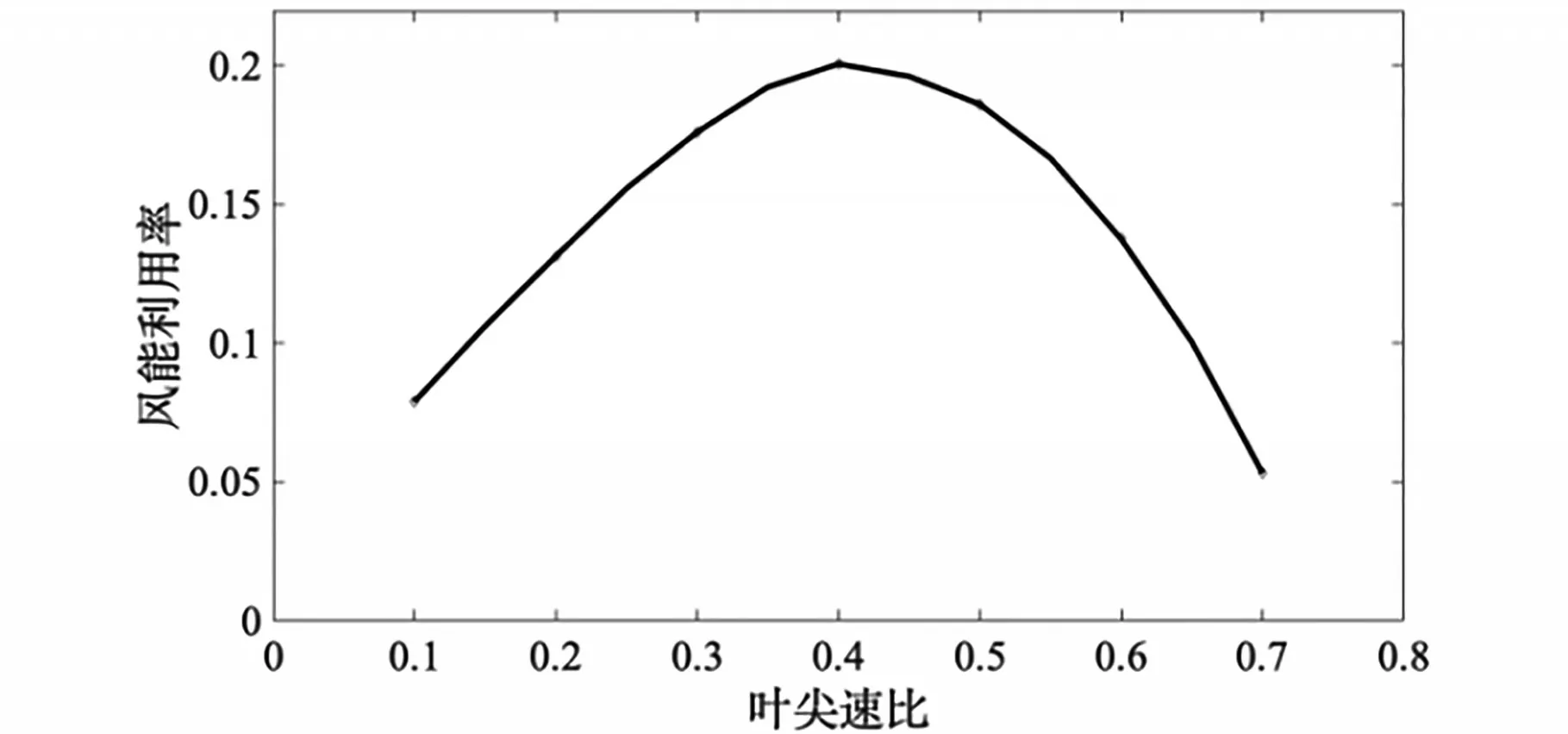
图10 叶尖速比—风能利用曲线Fig.10 Tip speed ratio—wind energy utilization curve

图11为一个旋转周期中风力涡轮机的三个叶片的转矩系数。TSR设置为0.23，风速为9 m/s。

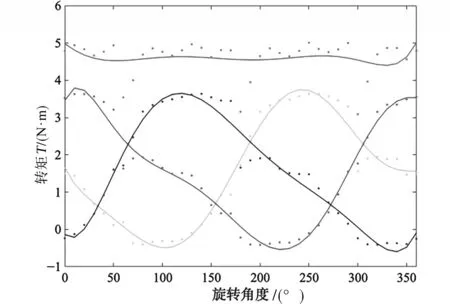
图11 三个叶片的转矩比较Fig.11 Torque comparison of three blades

从图11可以看出，图中的分散点是实际数据，通过仿真计算得出。根据散点图绘制的调整曲线大致为三个正弦曲线。由此可以得出结论，三个叶片始终存在一个叶片具有最大的作用，风力涡轮机的总输出转矩基本上稳定，并且转矩在4.5 N·m和5 N·m之间波动。

3.2 发电功率分析

仿真模型的输入风速设定为0～0.8 s内为6 m/s，0.8～1.5 s内为10 m/s，1.5～2.0 s内为8 m/s，设定风速如图12所示。仿真时长为2.5 s。发电机的定子相电阻为0.005 Ω，电枢电感为0.002 H，直流电压参考量为800 V，风机额定容量为25 kW，额定电网容量为20 kW。

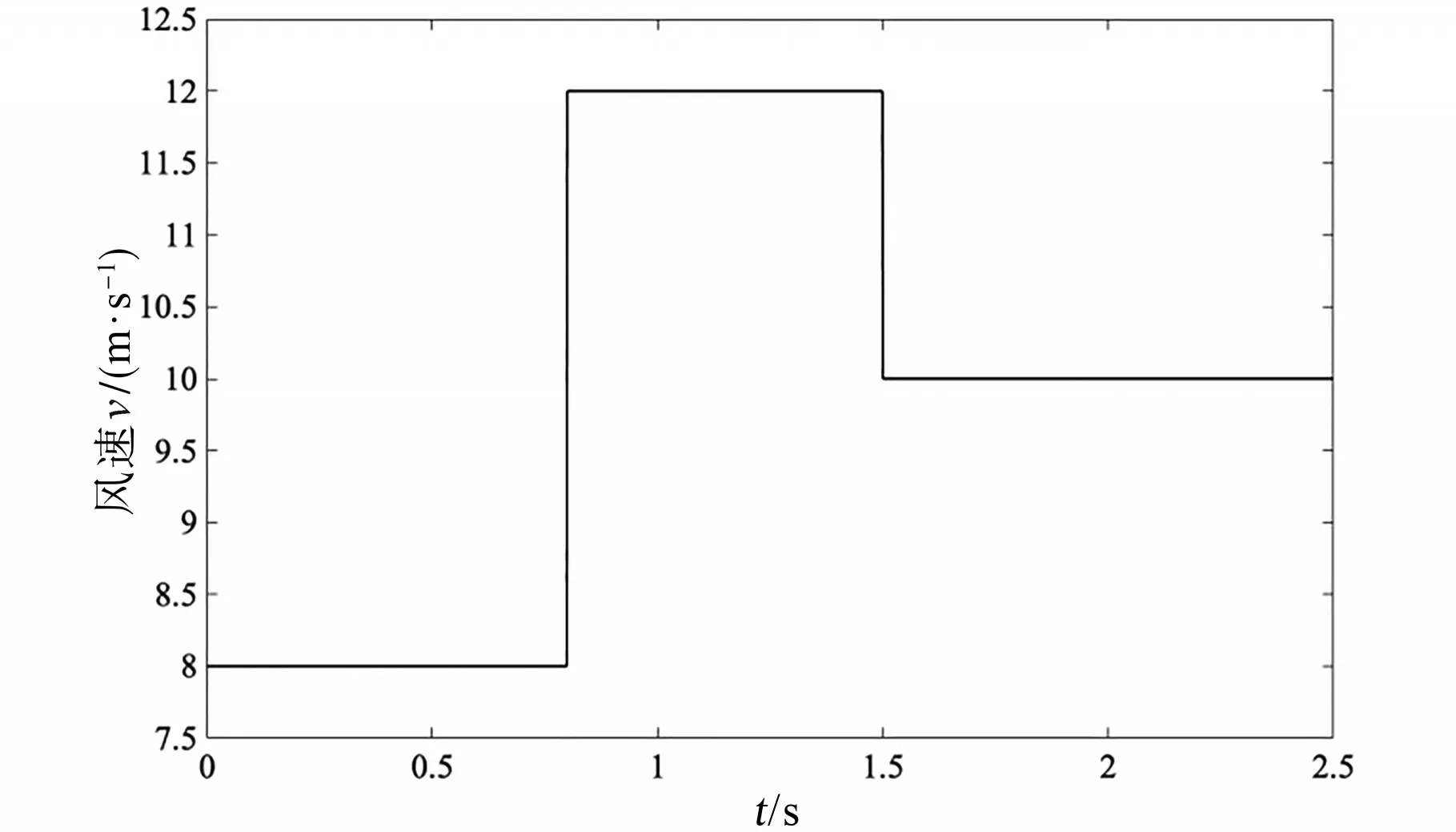
图12 设定风速Fig.12 Set wind speed

发电机输出转矩波形如图13所示。MPPT算法仿真对比如图14所示。由图13可知，风机输出转矩维持在1 000 N·m，在风速发生较大波动时，发电机转矩会出现暂时波动，并且在短时间内恢复至1 000 N·m，证明本文所用控制策略的有效性。

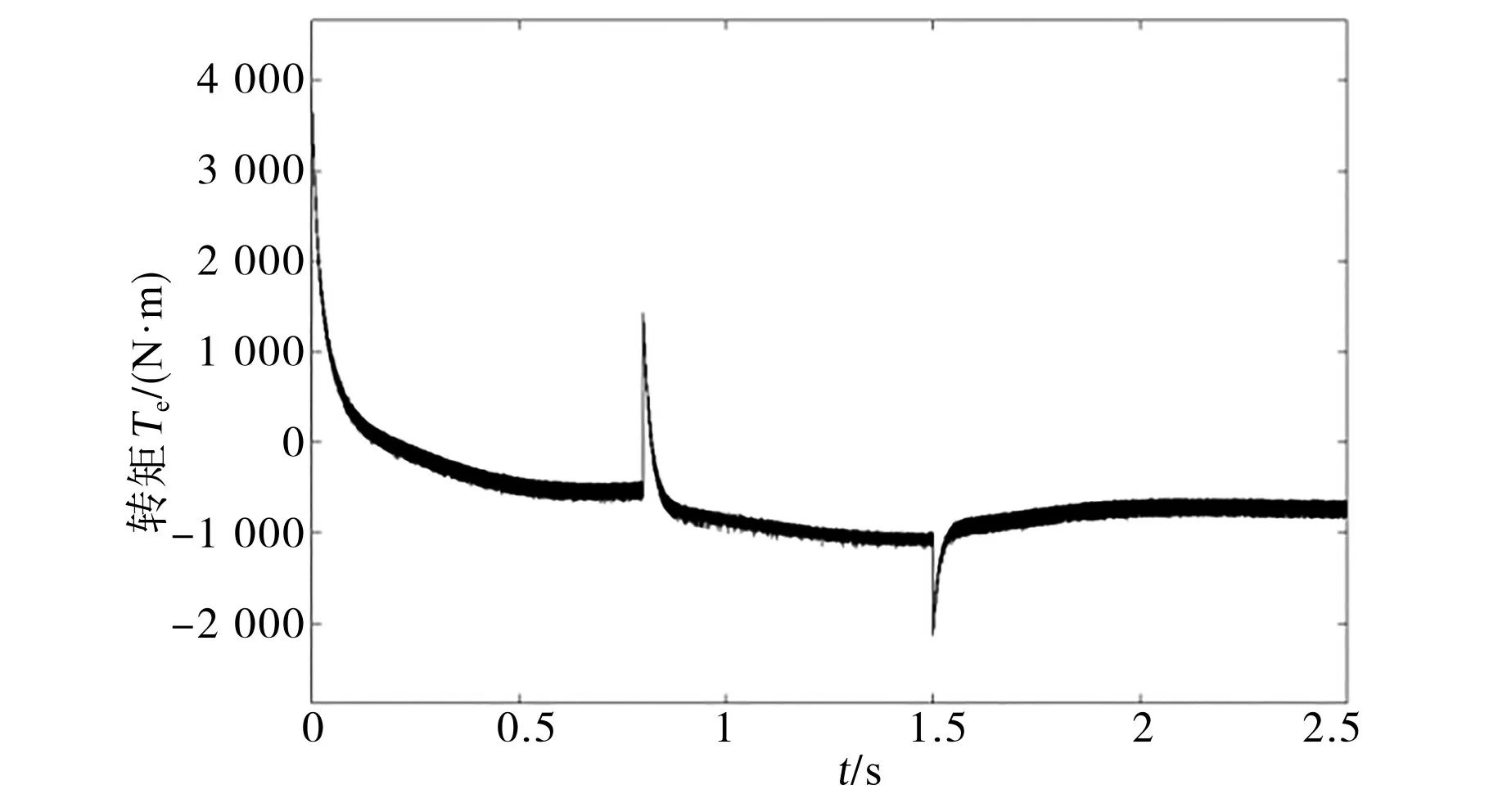
图13 发电机输出转矩Fig.13 Generator output torque

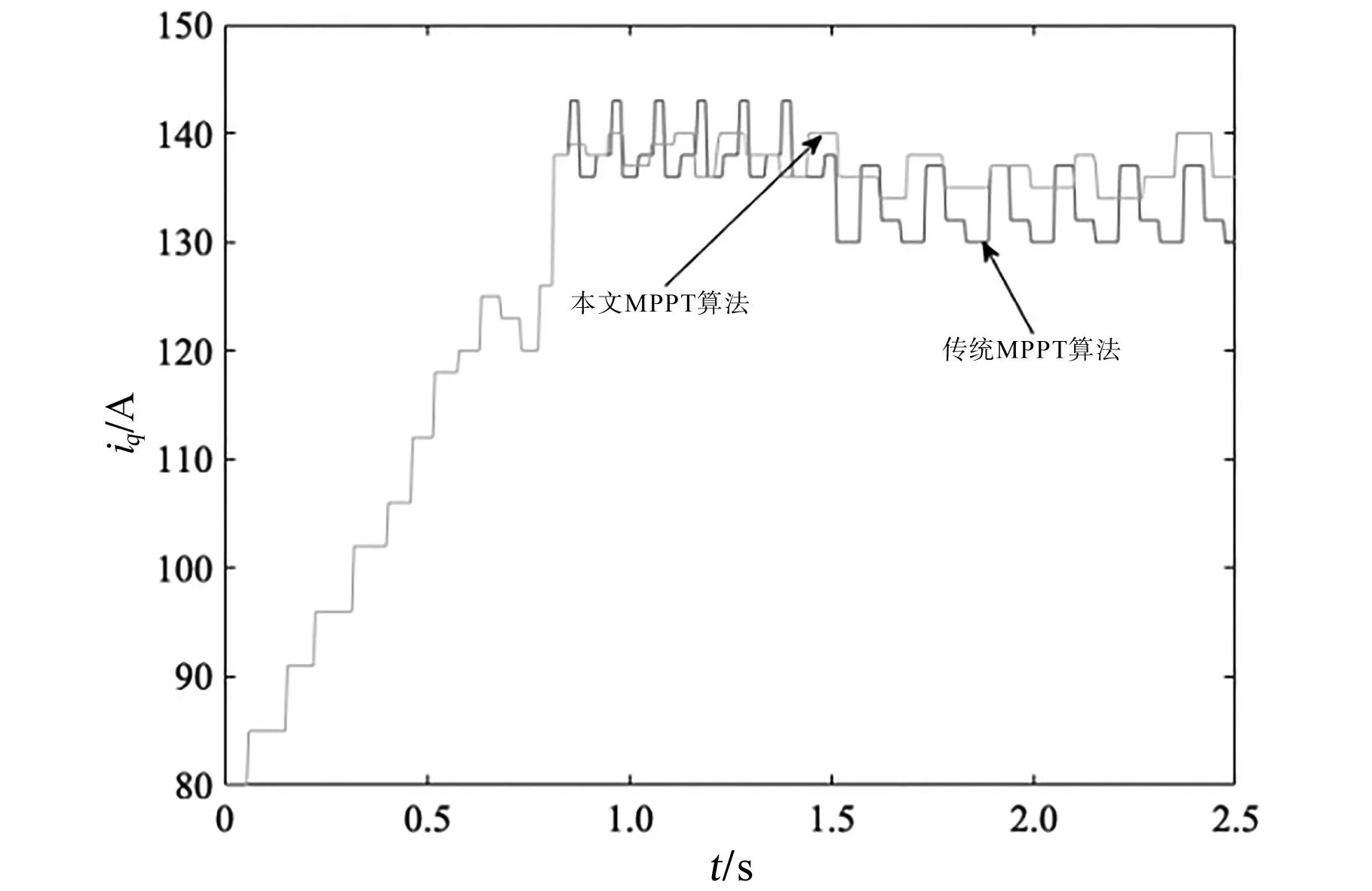
图14 MPPT算法仿真对比Fig.14 MPPT algorithm simulation comparison

由图14可知，在仿真中带有风速突变的情况下，本文所用功率跟踪算法较传统算法来看，显示出了准确度更高的性能，并且算法步长最终收敛于0，也验证了文中的公式计算结果。

图15为发电机输出三相电流波形。由图15可知，发电机所输出的三相电流为平滑的三相电，在风速发生突变的时间出现短暂波动，随后恢复50 A的交流电。图16为直流母线电压，从图16中可以看出大体维持在800 V左右，在风速波动后也很快恢复了正常电压，计算结果较为理想。

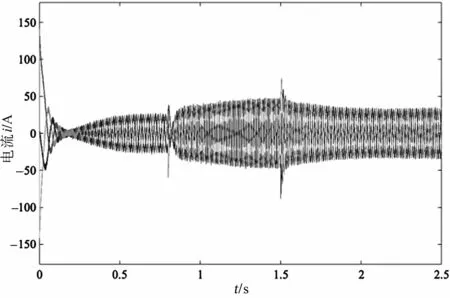
图15 发电机输出三相电流Fig.15 Generator output three-phase current

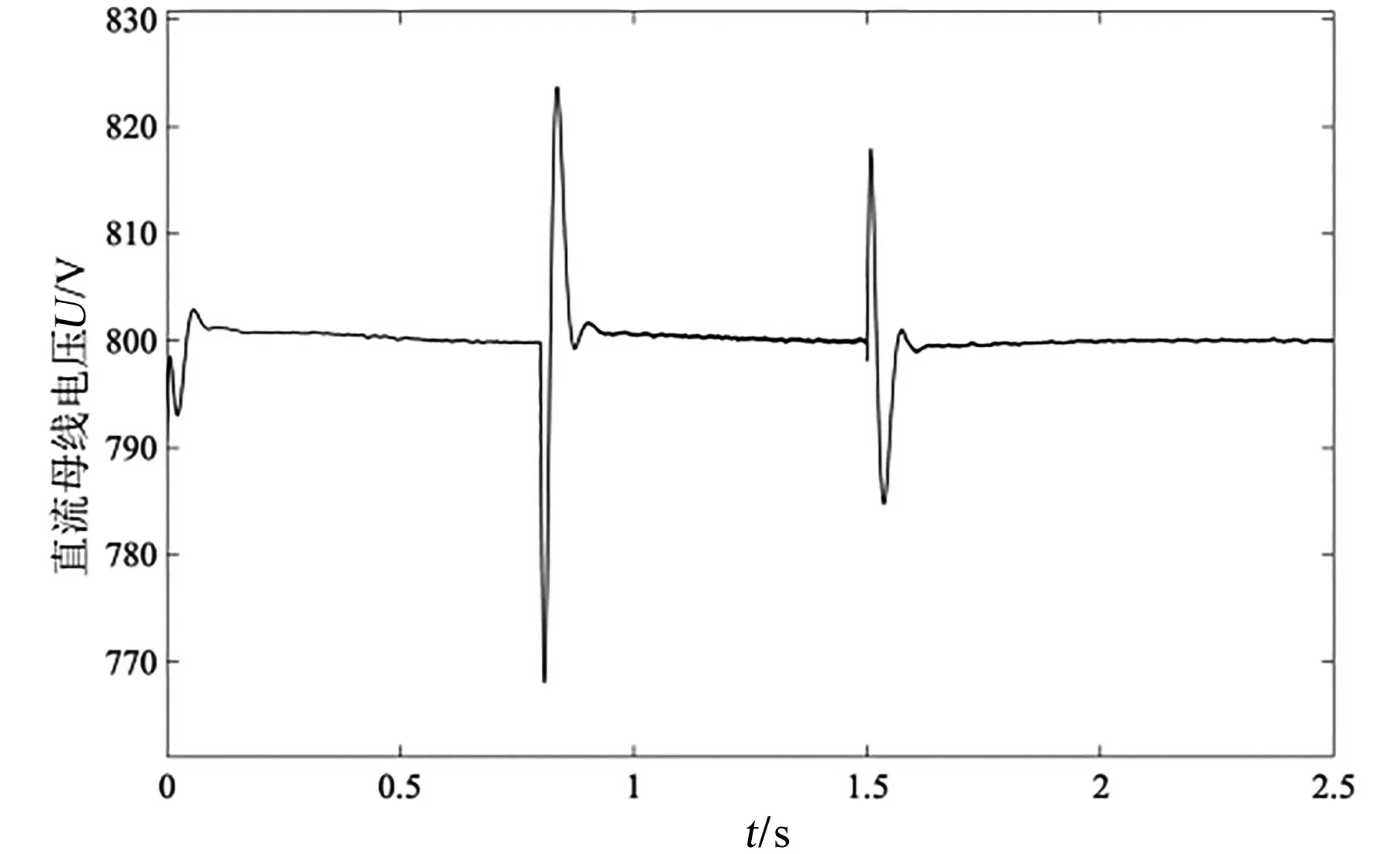
图16 直流母线电压Fig.16 DC bus voltage

图17为电网输出电压波形。图18为电网输出功率波形。由图17可得，在并网后电压可以维持300 V交流电，曲线较为平滑，并且在风速发生突变时曲线也没有发生较大波动，并且在图18中，电网在额定风速下输出功率在20 kW，符合预期的输出功率，证明了机侧/网侧控制方案的有效性，以及鹦鹉螺等角螺线型垂直轴风机在电网中的可靠性与稳定性。

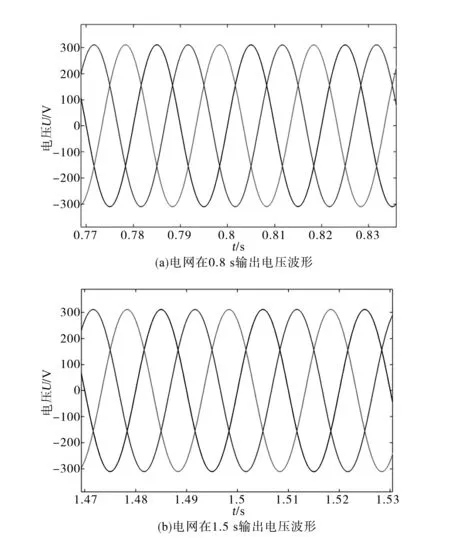
图17 电网输出波形Fig.17 Grid output voltage waveform

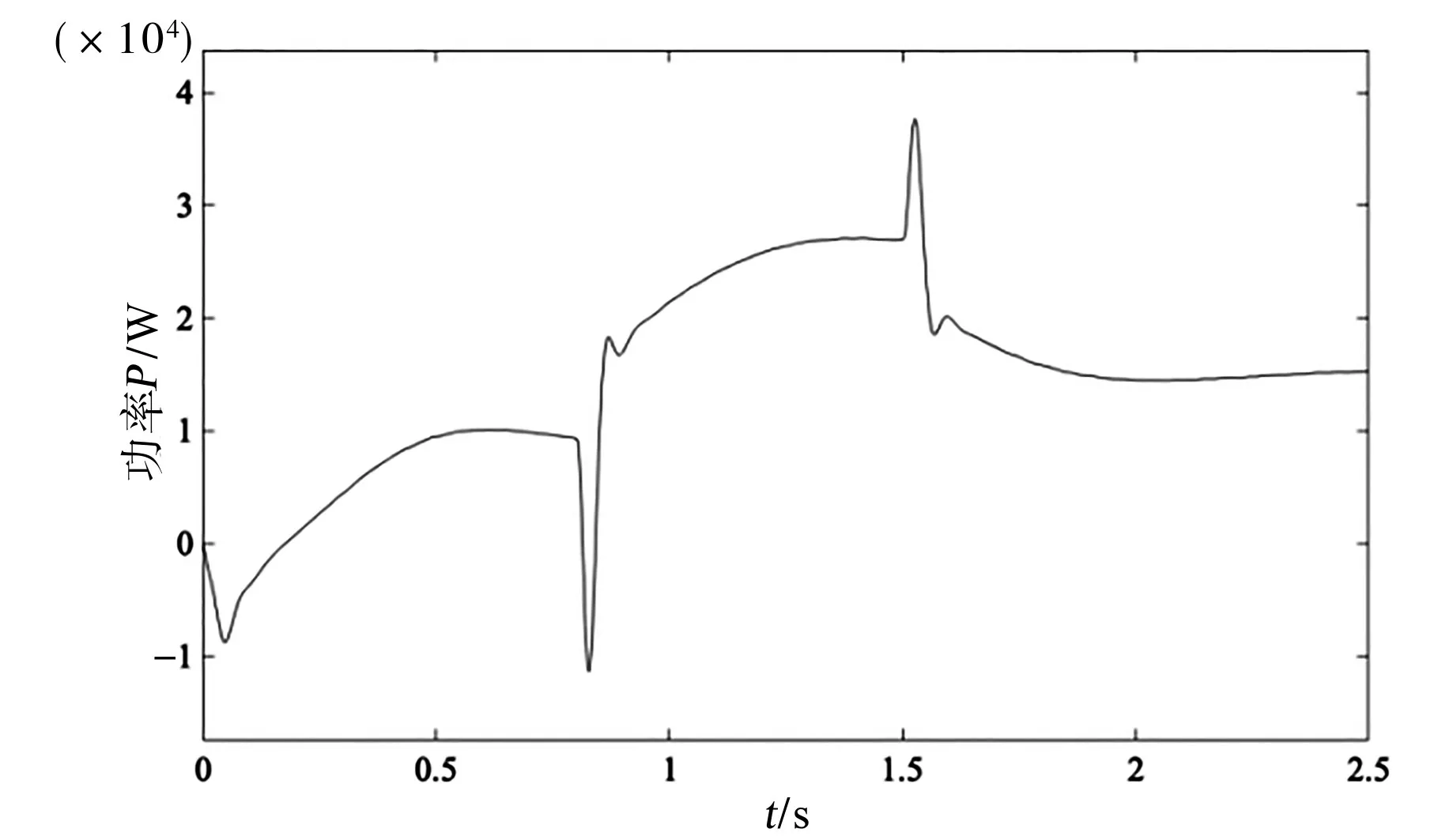
图18 电网输出功率Fig.18 Grid output power

4 结论

通过建立模型对鹦鹉螺等角螺线型垂直轴风机的性能以及并网参数进行了分析，分析结果符合预期。进行了流场分析，经过大量计算验证，本文所用模型在设定步长达到300步时，达到计算精度。根据发电机模型，建立了用于发电以及并网的控制系统仿真模型，并且加入了改变步长的最大功率跟踪法，经过仿真验证，此算法在风能并网中可以发挥其优良性能，证明在大型发电并网系统中，该类风机同样可以达到理想的效果和稳定性，证明了所建模型的有效性和鹦鹉螺等角螺线型垂直轴风机在发电系统中的可靠性及并网稳定性。