基于场景集的虚拟电厂中储能系统优化配置研究

李志浩，刘鑫，倪筹帷，葛晓慧，吴红斌

（1.国网浙江省电力有限公司电力科学研究院，浙江 杭州 310014；2.安徽省新能源利用与节能省级实验室（合肥工业大学），安徽 合肥 230009）

随着光伏（photovoltaic，PV）、风机等分布式电源大规模接入配电网，非化石能源发电成为未来电网的发展趋势。预计到2030年，清洁能源发电量占全国总发电量的49.2%。但分布式电源发电具有较大的随机性和波动性，给电网的运行与控制带来风险[1-2]。虚拟电厂（virtual power plant，VPP）是一种新型的分布式电源协调运行与管理技术，为解决上述问题提供了新方法[3]。其基本概念是通过聚合分布式电源、可控负荷和储能系统等分布式能源，作为一个可控发电商参与电网调度和电力市场交易[4]。为了解决分布式电源间歇性出力的问题，保证虚拟电厂供电的稳定性，在虚拟电厂规划建设阶段需充分考虑可控机组和储能系统的容量配置问题。但目前储能系统存在成本高、效率低、寿命周期短等问题，导致其在电力系统中的应用具有一定的局限性[5]。为了充分发挥储能系统在虚拟电厂中的作用，提高虚拟电厂运营收益，有必要对虚拟电厂中储能系统进行优化配置。

目前，国内外针对储能系统优化配置问题做了大量研究，文献[6]基于最小购电成本和储能损耗成本，建立了大规模光伏并网系统中储能容量配置模型。文献[7-8]在风电和储能联合运行系统中，建立了提高风电利用率的储能系统配置及调度模型。文献[9]考虑了随机生成和需求导致的存储容量决策问题的不确定性，对不同的需求和生成的储能系统配置进行了优化。文献[10]采用解析法和序贯蒙特卡罗模拟方法，对系统状态进行建模，找到最优的储能系统配置方案。文献[11]为了确保储能系统充分发挥多方面功能，建立了虚拟电厂中储能系统优化配置的多目标函数，并采用混合整数线性规划和粒子群优化算法进行求解。文献[12]采用蒙特卡洛与差分进化算法相结合的方式对高风电渗透率配电网中储能系统的位置和容量进行优化。文献[13-14]采用双层决策模型，以经济性最优为目标函数对储能系统进行优化配置，但其储能系统应用在用户侧，没有对虚拟电厂中储能系统的配置进行研究。

在上述背景下，提出了一种参与电力市场交易的虚拟电厂中储能系统随机优化模型，来确定储能的位置、容量以及电池类型。首先分析了虚拟电厂在电力市场交易过程中的不确定性，并采用蒙特卡洛抽样和场景缩减技术针对光伏出力的波动性、负荷需求的随机性进行不确定性建模。其次在虚拟电厂系统约束条件下，以储能系统投资成本最小为目标建立了双层优化模型，并采用粒子群算法和二阶锥规划理论进行求解。最后，利用改进的IEEE33节点系统验证了该优化配置方法切实可行并有效地提高了虚拟电厂在电力市场中的经济收益。

1 考虑不确定性的场景集生成

1.1 市场交易机制及虚拟电厂结构

由于相对于传统机组而言，虚拟电厂的出力可控性较低且自身容量有限，假设虚拟电厂仅参加日前电力市场和实时电力市场交易。在电力交易中心发布次日系统状况、负荷预测等市场信息之后，虚拟电厂需提交次日24个交易时段的售电报价、购电报价以及运行计划，与其他独立供电商共同参与市场竞争。虚拟电厂以交易中心的出清结果执行次日的发电计划，通过连接线与大电网相连进行功率传输。由于光伏发电和负荷存在波动性导致虚拟电厂出力存在一定的投标偏差，在次日的实时电力市场中虚拟电厂需以高于市场价的价格购电弥补缺额电量，以低于市场价的价格售电消纳富余电量。这无疑降低了虚拟电厂的运营收益，通过配置一定的储能装置，可以削峰填谷、提高分布式电源并网消纳量、降低网络损耗，进而提高虚拟电厂的经济性。所构建的虚拟电厂由光伏发电系统、燃气轮机、储能系统以及常规负荷组成，虚拟电厂系统的结构框图如图1所示。

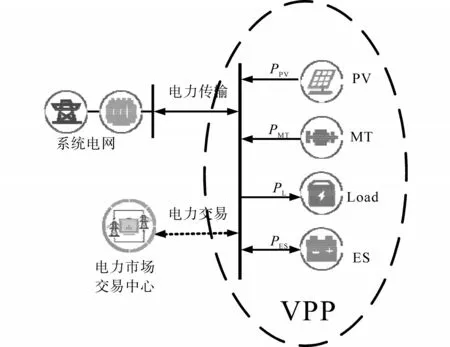
图1 虚拟电厂系统的结构框图Fig.1 Structure diagram of virtual power plant system

由于分布式电源出力和负荷预测的不确定性，储能系统的优化配置方法也是一个不确定性问题。采用蒙特卡洛模拟方法生成多个组合场景集，通过采样后计算期望值，进而将随机优化问题转化为确定性问题处理[15]。分别考虑光伏出力、负荷预测误差及燃气轮机运行状态场景集w={wi}i=1，2，…，nw；s={sj}j=1，2，…，ns；q={qk}k=1，2，…，n。其中nw，ns，nq为相应的场景集的个数，则总场景个数为nwnsnq。每个场景及其概率由一个离散分布函数表示。

1.2 光伏出力场景集

作为虚拟电厂中主要的发电单元，PV出力情况不仅与自身工作特性相关，更与当时的地理环境、光照强度等气候条件密切相关。由于太阳的光照强度服从Beta分布[16]，根据每个周期的平均光照强度计算分布参数α和β，随后采用蒙特卡洛抽样随机生成PV出力，其概率密度的分布函数如下[17]：

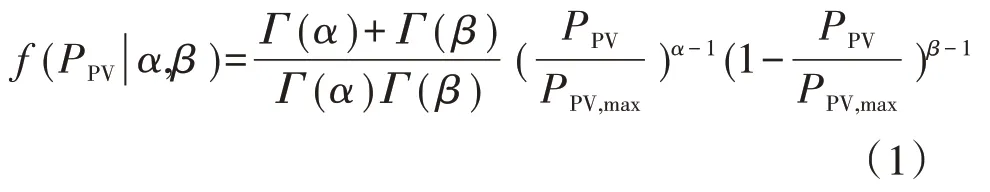
式中：PPV为PV的预测功率；PPV，max为PV的装机容量；α和β为Beta分布的形状参数。

由于PV发电在实际生产过程中存在误差，随机生成波动数据作为PV出力预测的误差值。光伏实际出力是光伏预测出力和预测误差值的叠加，如下式所示：

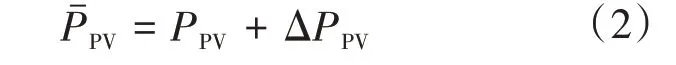
1.3 负荷预测误差场景集区

负荷预测也具有一定的误差，假设负荷预测误差服从高斯累积分布[18]，如下式所示：

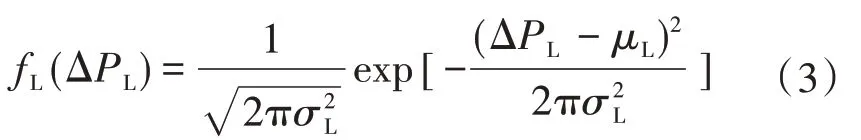
其中

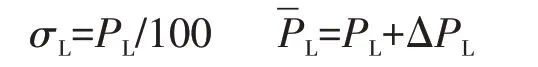
1.4 燃气轮机运行状态场景集

考虑到虚拟电厂系统内多台燃气轮机同时故障的概率非常小，只建立单台燃气轮机故障停运的场景集。采用双状态连续马尔科夫模型模拟燃气轮机在调度周期内的启停状态[19]，建立一台燃气轮机N-1故障场景集，其故障概率由下式确定：

式中：ni为正常燃气轮机编号；m为故障燃气轮机编号；qni为正常燃气轮机停机概率；qm为故障燃气轮机停机概率。

2 储能系统优化配置的双层规划模型

采用双层规划模型对虚拟电厂中储能系统进行优化配置。第一阶段，采用粒子群算法对储能系统的接入位置、容量以及电池类型进行优化。第二阶段，建立虚拟电厂优化调度的二阶锥规划模型，优化虚拟电厂内部分布式电源的小时出力，从而实现运行成本最小。第二阶段优化后得到的运行成本信息会传递到第一阶段，来计算相应的总成本。

2.1 上层优化模型

由于储能系统的接入位置、容量等技术指标不同，其对应的成本和效益也不尽相同，因此需要对储能系统的规划建设问题进行寻优，上层模型的优化目标包括储能系统的等年值投资成本、损耗成本和虚拟电厂运营成本。

2.1.1 目标函数

上层优化模型的目标函数由三部分组成，如下式所示：

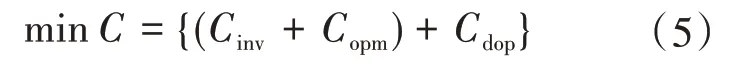
式中：Cinv为储能系统投资建设成本；Copm为储能系统运行维护成本；Cdop为虚拟电厂日常运营成本，由下层优化模型计算所得。

储能系统的建设成本与其装机容量耦合，可由下式计算所得：

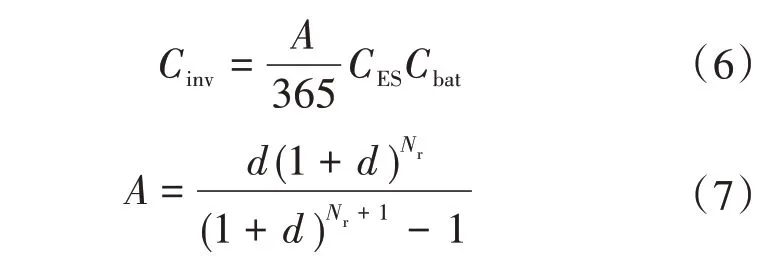
式中：A为等年值的初期投资成本系数；CES为储能系统单位容量的造价；Cbat为储能系统的装机容量；d为实际利率；Nr为储能系统使用年限。

储能系统的运行维护成本主要与其额定功率有关，且储能系统的额定功率与装机容量线性相关：

式中：kbat为储能系统额定功率与其装机容量的比例系数；Cop为储能系统单位容量的年运行维护成本。

2.1.2 约束条件

1）投资成本约束：

式中：Cinv，max为储能系统投资成本的最大值。

2）接入位置约束：

式中：ESlocation为储能系统接入节点编号；Φ为储能系统可接入节点集。

2.2 下层优化模型

在上层模型中确定了储能系统的接入位置、容量以及电池类型后，下层优化模型即可对虚拟电厂的运营策略进行优化。以不同场景下虚拟电厂日调度周期内损耗成本最小为目标建立优化模型。

2.2.1 目标函数

下层模型的目标函数如下：

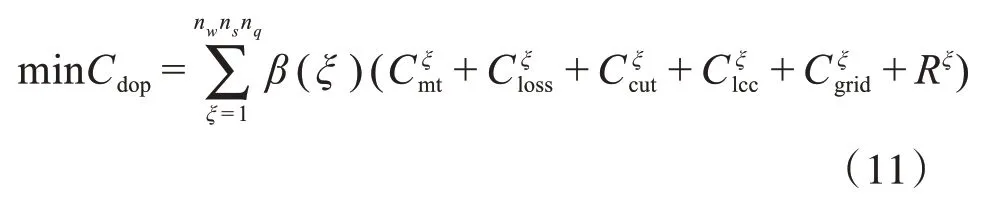
其中

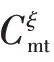
2.2.2 约束条件

1）系统功率平衡约束如下式：

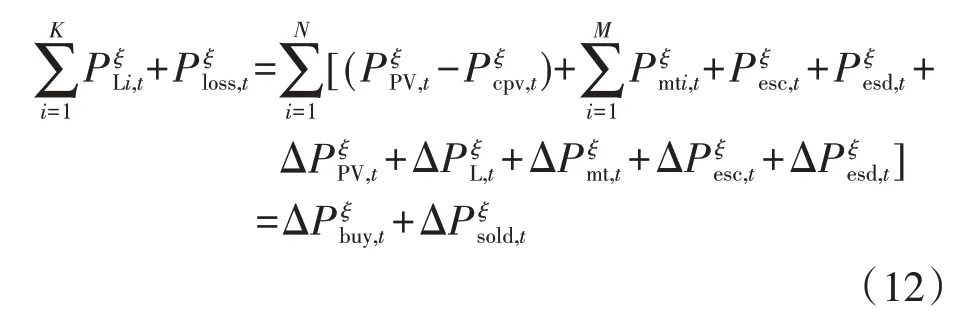
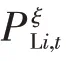
2）节点潮流约束如下式：

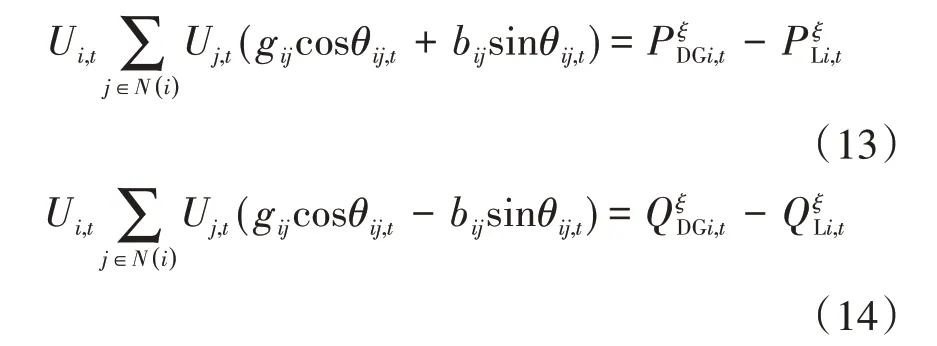
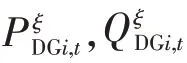
3）节点电压约束如下式：

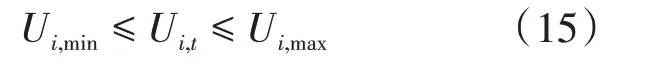
式中：Ui，min，Ui，max分别为t时刻节点i电压幅值的下限和上限。

4）燃气轮机出力约束如下式：

式中：Pmti,min，Pmti,max，Qmti,min，Qmti,max分别为t时刻节点i的有功、无功出力幅值的下限、上限。

5）光伏出力约束如下式：

6）储能系统约束如下式：

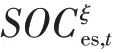
2.3 双层规划模型求解方法

以虚拟电厂运营总成本最小为目标函数建立双层优化模型，采用粒子群算法与CPLEX求解器相结合的方法进行求解。在上层优化模型中，采用粒子群算法对储能的接入位置、容量以及电池类型进行寻优。在下层优化模型中，调用CPLEX以虚拟电厂每日调度周期内运行成本最小为目标，优化储能系统充放电策略，将调度结果返回上层计算适应度值，经过多次迭代，从而得到虚拟电厂中储能系统的优化配置结果。但传统的虚拟电厂优化调度模型中包含非线性二次约束，需采用二阶锥优化将约束条件线性化[20-21]。二阶锥优化定义新变量如下：

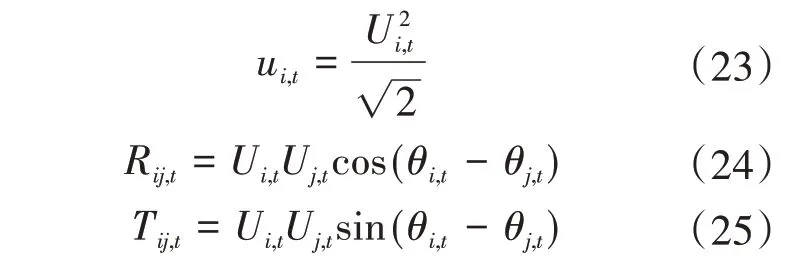
将新定义的变量代入式（13）、式（14）中，得到新的表达式及其约束：

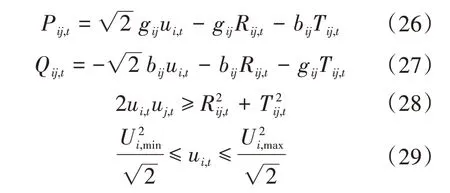
采用粒子群算法与CPLEX相结合的详细求解步骤如图2所示。

图2 求解流程图Fig.2 Solution flow chart

3 算例分析

3.1 算例系统

采用修改后的IEEE33节点系统作为一个虚拟电厂，对上述模型及算法进行仿真验证。系统结构图如图3所示，其中分布式电源的基本参数如表1所示。燃气轮机技术参数如表2所示。为简便起见可供储能系统选择的电池类型为锂离子电池和铅碳电池两种类型电池，其经济技术参数如表3所示。电力市场的出清电价[4]如表4所示，虚拟电厂不平衡功率的售电和购电电价，分别为在出清电价的基础上降低和提高20%。依据光照强度计算得到Beta分布的形状参数为α=0.45，β=9.18。生成光伏出力场景的个数nw=4，每个场景的概率均为0.25；负荷预测场景的个数ns=5，每个场景的概率均为0.2；燃气轮机场景的个数nq=3，各个场景的概率分别为0.5，0.4，0.1，则总场景数共计为60个。

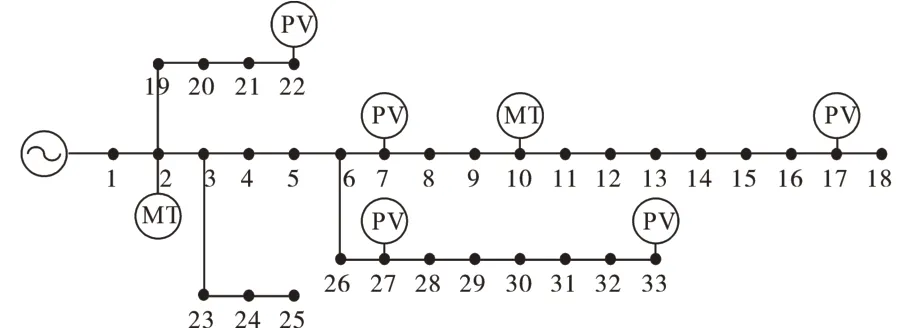
图3 IEEE33节点系统结构图Fig.3 The structure of the IEEE33 node system

表1 分布式电源参数Tab.1 Distributed power parameters

表2 燃气轮机技术参数Tab.2 Technical parameters of gas turbine

表3 经济技术参数Tab.3 Economic and technical parameters

表4 市场出清电价Tab.4 The price of market clearing

设置粒子群算法的学习因子为2，权重系数为0.8，种群规模为100，迭代次数为20。测试系统硬件环境为Intel Core i5-4590，主频为3.30 GHz，内存为8 GB，开发环境为Matlab R2017b，计算用时约为50～60 min。

3.2 优化配置结果

求解出的储能系统配置结果如表5所示。虚拟电厂中光伏出力、负荷预测结果以及储能系统最优出力曲线如图4所示。

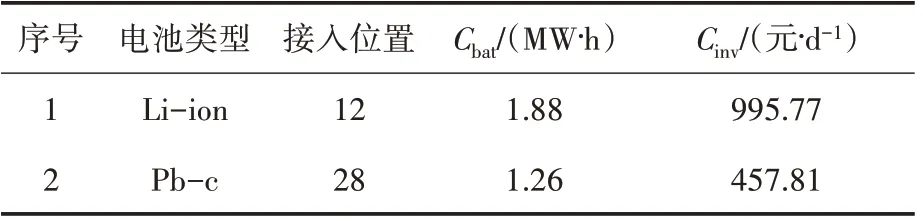
表5 储能系统配置结果Tab.5 Optimization allocation results of ESS

图4 储能系统最优出力曲线Fig.4 Optimal output curves of energy storage system

从图4中可以看出，虚拟电厂中的储能系统选择在电价较低的夜间时段进行充电，在白天时段，电价较高，储能系统进行放电。在7点到9点时间段内，光伏实际出力小于其预测功率，储能系统进行放电弥补功率偏差。在9点至11点时段内光伏实际出力大于其预测功率，储能系统进行充电，减少弃光损失，降低光伏出力波动性对虚拟电厂出力稳定性的影响。在13点至15点时段内实际负荷需求大于其预测值，造成虚拟电厂实时功率缺额，为了降低从电网购电的不平衡功率成本，储能系统进行放电。因此储能系统能够根据实际情况调整自身充放电行为，降低分布式电源出力和负荷预测的不确定性对虚拟电厂的影响。

虚拟电厂的电量交易曲线和燃气轮机出力曲线如图5所示。由图5可以看出在8点至15点时间段内光伏发电量大且电价高，虚拟电厂向电网售电，且在14点电价最高的时刻虚拟电厂售电量最大。在其它时间段内虚拟电厂由电网购电。在夜间时段，当电网电价降低到低于燃气轮机发电成本时，燃气轮机停止工作，虚拟电厂由电网购电量增大。

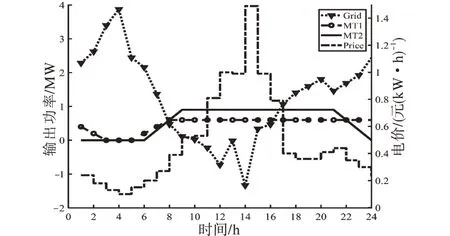
图5 虚拟电厂的电量交易曲线和燃气轮机出力曲线Fig.5 Electricity trading curves and gas turbine output curves of virtual power plant

3.3 经济性分析

采用粒子群算法对上述模型进行求解，其收敛性如图6所示。经过15次迭代后粒子群算法的适应度值达到最优，此时虚拟电厂每日的运营总成本为95 386元，相比于初始值降低了1 064元。说明文中的优化配置方法具有收敛性，且能够有效降低虚拟电厂中储能系统的日运行成本。

图6 PSO收敛特性曲线Fig.6 PSO convergence characteristic curve

为了验证该优化配置方法的经济性，设置三种场景。Case1：虚拟电厂中不配置储能系统；Case2：采用随机优化的方法对虚拟电厂的储能系统进行配置（在5号节点处配置2 MW·h储能，电池类型为Li-ion）；Case3：虚拟电厂中储能系统采用上述优化配置算法。不同方案下虚拟电厂日常运营成本如图7所示。由图7可以看出，Case3下虚拟电厂每日运营总成本最小，相比于Case1和Case2分别减少7 541元和4 121元。由于Case2和Case3中配置了储能系统，其弃光成本几乎降低为0，说明储能系统能够有效降低虚拟电厂运营成本。Case2和Case3中燃气轮机发电成本和弃光成本相比于Case1有所减小，这是由于储能系统可以在虚拟电厂电量过剩时存储电能，在电量缺额时作为分布式电源发电，说明该优化配置方法相比于现有的配置方案能够更好地对储能系统进行合理布置，使其充分发挥削峰填谷、提高分布式能源利用率的作用，从而提高虚拟电厂的运营收益。由图7中不难看出，Case3中虚拟电厂的平衡功率成本最低，说明采用该优化配置方案的虚拟电厂在电力市场交易中的不平衡功率最小，相比于Case1和Case2，该配置方案更加适应用电力市场的交易。

图7 不同方案下虚拟电厂日常运营成本Fig.7 Daily operating costs of virtual power plants under different scenarios

4 结论

提出一种虚拟电厂中储能系统的随机优化配置方法，以提高虚拟电厂运营收益。在充分考虑光伏出力波动性和负荷预测误差的基础上，采用蒙特卡洛抽样生成不确定性场景集。分别从规划和运行两个层次出发，建立了虚拟电厂中储能系统的双层优化模型。上层以储能系统的综合建设成本最小为目标函数，下层以虚拟电厂的日运行成本最小为目标函数，采用粒子群算法结合二阶锥优化进行求解。并在建立模型的过程中充分考虑了储能系统损耗成本，电力市场惩罚机制等约束条件。通过改进的IEEE33节点系统，分析了储能系统不同配置结果对虚拟电厂经济性的影响，并给出了虚拟电厂内各分布式电源的最优功率曲线，验证了该模型和方法的有效性。