定子磁场定向异步电机弱磁运行特性研究

贺艳晖

（中车株洲电机有限公司，湖南 株洲 412005）

在许多工业应用场合，比如数控机床的主轴电机、电动汽车、高速离心透平机械等，都要求驱动电机有比较宽的恒功率弱磁运行区域，具有一定的转矩输出能力和良好的动态转矩响应性能[1-4]。转子磁场定向控制法对电机参数有较强的依赖性[5-8]，而定子磁场定向控制系统只与定子电阻有关，在弱磁运行时与电机的饱和程度无关，具有更好的电机参数鲁棒性[9-10]。

异步电机在基速以下时保持磁通恒定，其最大输出转矩仅受电机额定电流和逆变器最大允许电流限制；而在基速以上时，随着绕组反电势的增加，必须进行弱磁控制，使电压达到可控范围内的平衡。文献[11]推导出了电压和电流约束条件下电机励磁电流轨迹和转矩电流轨迹的解析计算值。文献[12]在考虑电压、电流的限制条件下，利用不同弱磁运行区间转矩电流限制的不同，实现了合适的电流优化控制策略。文献[13]提出了一种最优定子磁链计算方法，该方法基于定子磁场定向控制异步电机稳态数学模型直接计算定子磁链指令值，保证了电机同时工作在电压极限和转矩极限，从而使电机具有最大转矩输出能力。文献[14]把异步电机的弱磁运行区域划分为两个弱磁区域，利用定子电压闭环控制器获得磁链参考值，使电机在整个弱磁区域工作在电压极限，在弱磁运行区域一通过电流限幅保证电机工作在电流极限，在弱磁区域二运行时，通过负载角控制器来减小定子电流的幅值，以保证电机稳定运行在失步转矩工作点。该策略能完全利用电压和电流的极限值，整个弱磁运行范围能够产生最大的稳态转矩并具有快速的动态响应能力。然而这种控制方法需要增加控制环和控制变量，使得控制算法比较复杂，而且负载角的计算与电机的漏感有关，失去了定子磁场定向控制的一个最大的优点。R.Bojoi[15]提出一种定子磁场定向弱磁前馈控制策略，同时考虑了电流、电压和转矩极限值，在有限且变化的直流侧电压条件下计算出最优定子磁通参考。通过d轴电压控制定子磁通而不需要电流控制环，通过q轴电流限幅值来自动完成转矩的限幅，对参数的依赖性比较小。

上述基于定子磁场定向控制的弱磁控制策略都能实现电机在弱磁运行区域的最大转矩输出，但上述控制策略对弱磁区域运行时电机电压、电流及其功率随定子频率的变化规律只是做了一些定性分析，没有详细的理论推导。本文对定子磁场定向异步电机弱磁区域最大转矩控制进行了详细分析，得到了电机电压、电流和功率随定子频率的变化规律，为弱磁区域控制提供了理论基础与研究思路。最后，搭建试验系统验证了理论分析的正确性。

1 弱磁区域运行限制条件

异步电机在运行时受到电机或变流器所允许的最大电压和最大电流限制，即电机定子相电压和线电流的峰值应满足：

式中：|us|为定子相电压幅值；usd为定子电压d轴分量；usq为定子电压q轴分量；Umax为定子相电压的限幅值。

式中：|is|为定子线电流幅值；isd为定子电流d轴分量；isq为定子电流q轴分量；Imax为定子线电流的限幅值。

对于定子磁场定向控制下的异步电机来说，还存在转矩极限的限制。相比于异步电机T型等效电路，通过其Γ型等效电路可以更直接推导出定子磁场定向控制时电机的转矩极限。Γ型等效电路如图1所示[16]。

图1 异步电机Г型等效电路Fig.1 TheГ-type equivalent circuit model of induction motor

图1中ωe为d，q轴同步旋转角频率；Ψs为定子磁链；ΨR为转子磁链；Us为定子电压；Is为定子电流；Rs为定子电阻；IM为励磁电流；IR为转矩电流；s为转差率。

Г型等效电路与T型等效电路中电机参数的转换关系如下所示：

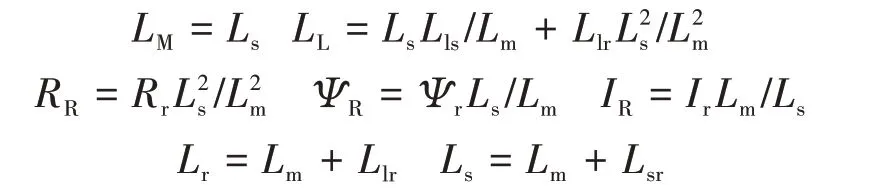
式中：Lm，Lls，Llr，Rr，Ir，Ψr分别为T型等效电路中电机的定转子互感、定子漏感、转子漏感、转子电阻、转子电流和转子磁链；Lr为转子自感；Ls为定子自感。

可以推导出定子磁场定向控制时电机的转矩极限Te_max：

式中：np为电机极对数。

在最大转矩时的电机转差率：

为了保证电机稳定运行，电机的转矩不能超过最大转矩Te_max，转差率不超过最大转差率sm。

2 弱磁区域电机特性分析

根据文献[17]，把弱磁运行区域划分为弱磁区域一和弱磁区域二。为了更充分利用逆变器容量，在弱磁区域一运行时，电机要同时工作在电压极限和电流极限以保证电机能够输出最大转矩。在弱磁区域二运行时，电机一直工作在最大转差率sm点以保证电机的稳定运行，而且为了获得最大的转矩输出，电机同时工作在电压极限。

2.1 弱磁运行区域一电机特性分析

根据Г型等效电路，可推出异步电机的阻抗角：

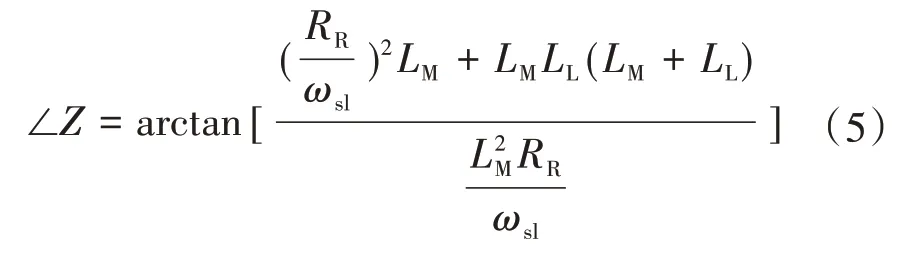
其中

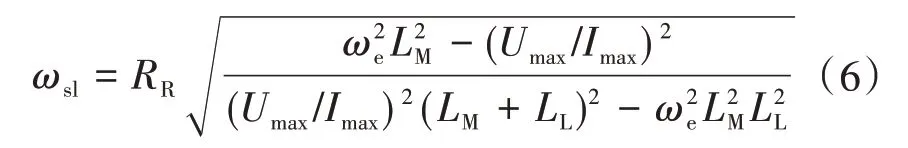
式中：ωsl为转差角频率。

令RR/ωsl=x，则式（5）可改写为

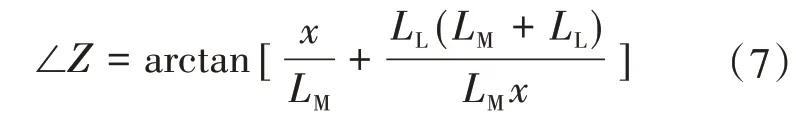
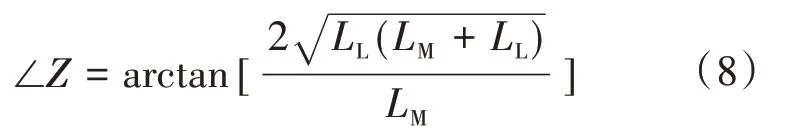
此时，同步角速度为

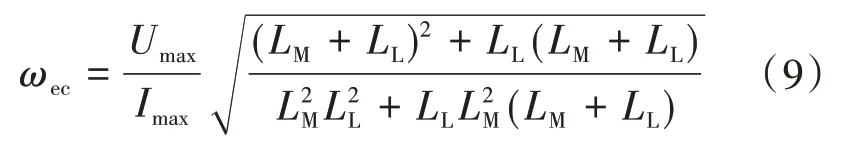
由电机阻抗角的变化规律可以得到弱磁区域一运行时电机的电压、电流和功率变化矢量图如图2所示。图2a为弱磁区域一运行时电流矢量的变化图。由于电机在弱磁区域一工作在电流极限，因此定子电流的幅值不变，电流矢量只能沿着圆弧AOB运动，圆弧半径为电流的限幅值，由式（5）可知电流矢量首先从O点沿着圆弧向A点运动，isd减小，isq增加，当同步角速度大于ωec后，电流矢量沿着圆弧开始向B点运动，isd增加，isq减小。由于定子电压幅值保持不变，而励磁回路的阻抗则随着同步转速的增加而不断增大，因此随着同步角速度的增加，励磁电流IM一直减小，而转子电流（转矩电流）IR则不断增大。弱磁区域一运行时电机电压矢量变化图如图2b所示。由于电机在弱磁区域一工作在电压极限，忽略定子电阻压降，转子电压沿着圆弧COD向D点运动，圆弧COD的直径为定子电压限幅值。在电压和电流限制下，弱磁区域运行时电机的转差率一直增大，转差角频率也在不断增大，转子回路的等效电阻值变小。由图2a分析可知转子电流IR随着同步角速度的增大而不断增大，因此电机漏抗上的压降随着同步角速度的增大而不断增大，转子等效电阻上的压降则不断减小。由于电机在弱磁区域一既工作在电压极限又工作在电流极限，因此其视在功率保持不变，如图2c所示，视在功率沿着圆弧EOF运动，先从O点沿着圆弧向E点运动，有功功率增大，无功功率减小，当同步角速度大于ωec后，从O点沿着圆弧向F点运动，有功功率减小，无功功率增大。

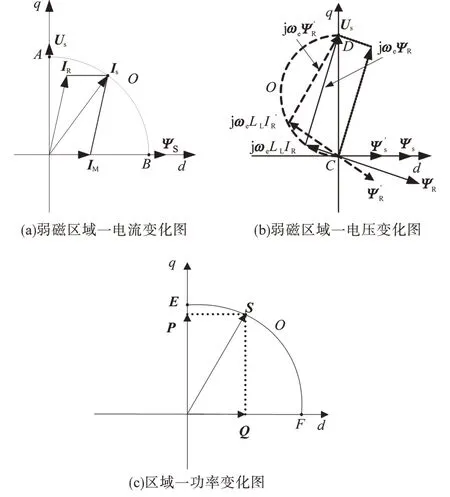
图2 定子磁场定向弱磁区域一的电机特性分析Fig.2 Characteristic analysis of induction motor in stator flux-oriented field-weakening regionⅠ

2.2 弱磁运行区域二电机特性分析

在弱磁区域二运行时，为了保证电机稳定运行，电机必须一直工作在最大转差率sm点，而且为了获得最大的转矩输出，在弱磁区域二运行时电机应该同时工作在电压极限。此时，电机稳定运行于最大转差值ωsl_m，维持为恒定值，由式（4）可得到最大转差值，如下式所示：

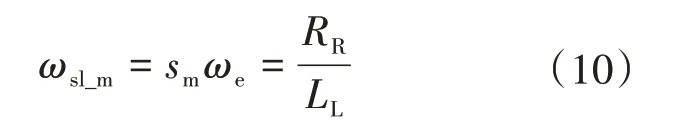
由式（6）和式（10）可得到第二个弱磁区域转折频率如下式所示：

电机在弱磁区域二工作时，电机工作在极限转矩，此时电机漏抗和转子等效电阻的大小相等，因此漏抗上的压降和转子等效电阻的压降相等，转子电流与定子电压的夹角恒为45°（忽略定子电阻压降的影响）。由于在弱磁区域二电机定子端电压为电压极限，而定子端电流则随着同步转速的增加而不断减小，因此在弱磁区域二，电机的视在功率一直减小，有功功率和无功功率都减小，且无功功率与有功功率相等。

由于在弱磁区域二最大转矩运行时定子电压和转子电流的夹角恒为45°，忽略定子电阻压降，转子电流和定子电压的夹角等于定子磁链和转子磁链的夹角，因此可以通过维持定子磁链和转子磁链的夹角恒为45°来限制定子电流，保证弱磁区域二的稳定运行。

3 定子磁场定向弱磁控制实现

在弱磁区域运行时异步电机定子磁场定向控制框图如图3所示。采用文献[17]的弱磁区域的最大转矩输出策略。在此基础上，为了获得快速的磁链响应速度，磁链环和d轴电流环不限幅，只对速度环和q轴电流环限幅。

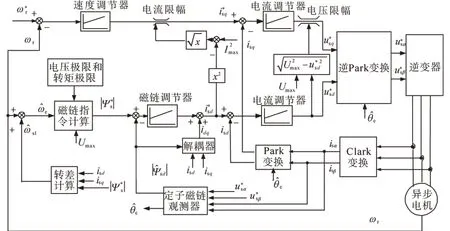
图3 在弱磁区域运行时异步电机定子磁场定向控制框图Fig.3 The block diagram of stator flux-oriented control for induction motor in field-weakening region

定子磁通观测器采用带补偿低通滤波器磁链观测方法[18]。电机相电压通过逆变器开关函数和直流侧电压计算得到[19]。通过检测电机电流的方向，在每相电压上加上与误差电压相同的电压补偿量消除死区效应引起的电压误差[20]。

定子磁场定向时，电机转差角频率ωsl由下式计算得到[21]：

其中

σ=1-L2m/(LrLs)τr=Lr/Rr

同步转速估计值ωe由下式计算得到：

式中：ωr为电机转速角频率。

加入电流的解耦项idq如下式所示[15]：

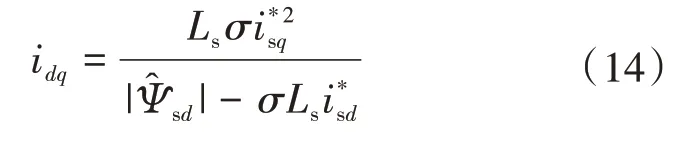
式中：*表示控制产生的指令值或给定值变量。

4 仿真研究

由设置的电机参数和Umax,Imax值，通过式（9）和式（11）可得到转折频率理论值分别为ωec=430 rad/s，ωec_2=1 041 rad/s，最大转 差 角频率ωsl_m=99.7 rad/s。

异步电机在弱磁运行区域采用最大转矩控制策略时的仿真结果如图4、图5所示，曲线1为灰色，曲线2为黑色。

图4 同步转速、磁链跟踪和电流跟踪的仿真波形Fig.4 Simulation waveforms of synchronous speed，flux tracking and current tracking

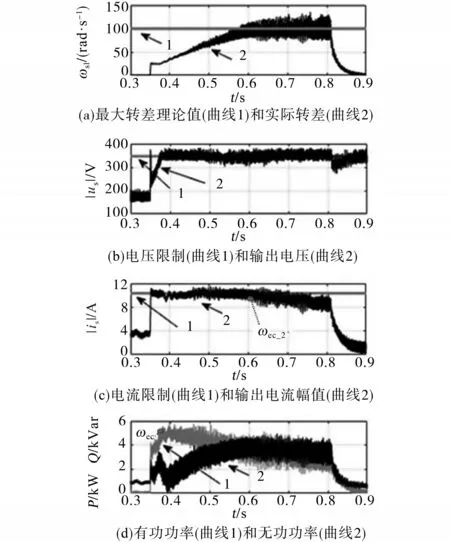
图5 转差、电压极限、电流极限和功率的仿真波形Fig.5 Simulation waveforms of slip angle speed，voltage limit，current limit，and motor power

图4为电机定子同步角速度、磁链跟踪、d轴电流跟踪和q轴电流跟踪的仿真波形。图5为电机转差、电压极限、电流极限和功率的仿真波形图。

由图4、图5可知，电机在0.37 s进入第一个弱磁运行区域，随着同步转速的升高，isd减小，isq增大，电机有功功率增大，无功功率减小。同步转速升到ωec的时刻是0.39 s，当同步转速大于ωec（仿真中ωec为420 rad/s，理论值为430 rad/s）后，isd增大，isq减小，电机有功功率减小，无功功率增大。在整个弱磁运行区域一，电机同时工作在电压极限和电流极限，电机的转差一直增加，定转子磁链夹角也一直在增加。在0.63 s，电机同步角速度上升到ωec_2（仿真中ωec_2为1 020 rad/s，理论值为1 041 rad/s），电机进入第二个弱磁区域，定转子磁链的夹角到达44°（理论值为45°），电机转差增加到97 rad/s（最大转差ωsl_m理论值为99.7 rad/s）。随着同步速的进一步升高，isd和isq都减小，电机有功功率和无功功率也都减小。在整个弱磁运行区域二，电机同时工作在转矩极限和电压极限，电压极限和转矩极限重合。定转子磁链夹角稳定在44°（理论值近似为45°），转差一直维持在最大转差点。此时电机不再在电流极限上工作，电机降功率运行，而电机的无功功率和有功功率大小近似相等。

可以看出，在整个弱磁运行区域，电流和磁链的跟踪性能非常好，电机输出转矩为理论计算的弱磁区域运行最大转矩。弱磁区域的两个转折频率与理论值相比，误差不超过3%，电流、电压和功率的变化规律及定量分析结果与理论分析非常吻合，验证了理论分析的正确性。

5 实验研究

实验平台如图6所示。主电路由三相不可控整流电路和三相全控桥组成，变流器采用的是IGBT-IPM（型号为7MBP75RA120）的功率模块。采用LEM电压霍耳传感器检测直流侧电压，采用两个LEM电流霍耳传感器检测定子相电流。电机实际转速通过光电编码器测量得到。采用它励直流发电机带电阻的形式施加负载。试验中异步电机参数见第4节的电机参数设置。

图6 实验平台总体框架图Fig.6 The diagram of the experimental platform

功率模块开关频率为2 kHz，控制系统中定子电流的采样周期和电流环控制周期为500 μs，磁链观测和同步角速度的计算周期为500 μs，磁链环控制周期为2.5 ms，速度环控制周期为10 ms，死区时间为4 μs，磁链观测器的时间常数为0.023 84 s。

由于电机最高的安全运行转速只有3 000 r/min，因此在实验中电机最高运行到3 000 r/min，没有进入到弱磁运行区域二（电机转速大于4 464 r/min）。试验中，电机空载，转速指令从900 r/min阶跃至3 000 r/min。

图7为定子磁链Ψsd和同步转速ωe。在最小阻抗角时的同步角频率ωec=387 rad/s，ωec的理论值为405 rad/s，误差约为4.5%。由于电机参数是通过传统离线辨识方法得到的，与设计值存在一定误差，而且在弱磁区域电机电感参数也会变化，导致与理论值的误差相对仿真时变大。

图7 定子磁链和同步角速度试验波形Fig.7 Experimental results of stator flux and synchronous angle speed

图8为定子电流d，q轴分量跟踪性能试验波形以及电机相电流波形。电机在弱磁区域运行时，电流跟踪特性非常好，不会出现电流失控现象，d轴电流在进入弱磁区域一时首先下降，当同频角频率达到ωec后，d轴电流开始增加，而q轴电流变化规律与d轴电流相反，电流变化规律与理论分析相一致。

图8 电流跟踪性能与相电流试验波形Fig.8 Experimental results of current tracking performance and phase current

图9为定子电压指令幅值Us_max和实际定子电流幅值Is_max的实验波形。在弱磁运行时，定子电流幅值为9.7 A左右，定子电压指令幅值为300 V左右。由于电机参数存在误差，磁链前馈计算值并不是真正的最优磁链值，导致实际运行的电流幅值与电压幅值与理论的极限值（10.3 A，310 V）出现了大约6%左右的误差。

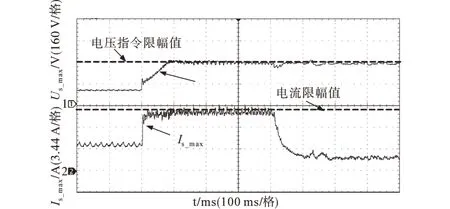
图9 电压幅值和电流幅值试验波形Fig.9 Experimental results of voltage magnitude and current magnitude

6 结论

1）通过定量分析得到弱磁区域运行时电机的最小阻抗角和转差频率解析表达式，以及两个弱磁区域电机运行的特征与电压、电流和功率的变化规律。

2）在弱磁区域一电机运行在电压、电流极限，在最小阻抗角定子电流的变化趋势发生转折。弱磁区域的两个转折频率ωec的仿真结果与理论值相比，误差不超过3%，定子d，q轴电流变化规律与理论分析完全吻合。

3）在弱磁区域二电机运行在最大转差频率ωsl_m时，定、转子磁链夹角恒定为45°，无功功率与有功功率相等。仿真结果与理论分析结果完全吻合，最大转差频率ωsl_m和定转子磁链夹角的误差都不超过3%。

4）搭建了异步电机弱磁控制试验系统，实现了定子磁场定向异步电机弱磁区域一最大转矩输出。电机内部变量的变化规律与理论分析一致。由于电机参数存在误差，转折频率与理论值误差为4.5%，实际电压电流幅值与理论极限值误差约为6%左右。