一种高效VIENNA整流器断续调制方法

李伦全，杨奕帆，李佳窈，刘斌，李小文

（1.深圳市高益智能电气有限公司，广东 深圳 518101；2.南昌航空大学 信息工程学院，江西 南昌 330063；3.国网南昌市昌北供电公司，江西 南昌 330063）

VIENNA整流器是一种中点钳位式三电平整流器拓扑[1]，其具有开关器件少、能实现稳压和输入功率因数校正等优点，近年得到了广泛的应用[2]。

针对VIENNA整流器，文献[3]研究实现了三电平等效为两电平的转化，故可以使用两电平扇区的判断方法，以及相关矢量的作用时间计算方式。文献[4]将其他扇区的参考矢量统一转化到第1扇区，提高了运算速度。文献[5]提出了一种可直接实现VIENNA整流器空间矢量脉宽调制（space vector pulse width modulation，SVPWM）的数学优化方法，并进行了验证。VIENNA整流器的控制方法以及调制方式有较好的研究价值，随着功率器件开关频率的不断增加，开关损耗对系统效率的影响也增大，通过优化调制技术可以降低整体开关频率。

针对大功率并网逆变，文献[6]提出一种混合断续PWM调制策略，能有效控制中点电位平衡，而两种调制算法的切换采用滞环方式，并减小切换造成的额外开关动作，提升了系统效率。为降低开关损耗，文献[7]提出一种三电平断续脉宽调制策略，进而提出一种基于载波思想的实现方法，有利于提高芯片计算的运行效率。VIENNA整流器输出正或负电压时，与当前时刻的电感电流方向有关，相较于一般全控型逆变或功率因数校正（power factor correction，PFC）系统的断续调制，多了一个隐含的约束条件。文献[8]首先对VIENNA整流器提出无差拍控制器，并将输出送到不连续脉宽调制（discontinuous pulse-width modulator，DPWM）中，实现系统的断续调制，但该文对断续调制与输出电流的关系，以及中点电位平衡的具体实现办法等问题，尚未进行深入讨论。相关的研究还可参考文献[9-10]。

本文在介绍了VIEENA整流器模型及控制器设计的基础上，提出一种新型的断续调制算法。一方面，结合整流器各相电流符号，研究能在若干分区内实现最大电流相开关不动作；另一方面，该调制算法也对如何进行中点电位控制进行了分析，通过在无法实现最大电流相开关不动作的小区中，引入一个角度控制量，在该角度范围内进行中点电位控制，而在该角度之外，也实现某相的开关不动作，尽量提升系统效率。最后通过仿真和实验对所提调制算法和控制器进行了验证。

1 三相三线VIENNA拓扑及空间矢量分布

1.1 主电路拓扑及模型

三相三线VIENNA主电路拓扑如图1所示，不失一般性，假设三相电压对称。图1中A，B，C三相电网相电压的值为eA，eB，eC，三相电流为iA，iB，iC；D1～D6为整流二极管，Q1/Q2，Q3/Q4，Q5/Q6分别为A，B，C三相的反向串联开关管，这3对开关管的驱动为SA，SB，SC；直流母线电压的值为Udc；直流母线电容由C1和C2串联构成；i1为二极管D1/D2/D3的总电流；i2为二极管D4/D5/D6的总电流。设电感L1，L2，L3的值相等，都为L；C1和C2的值都为C；负载电阻为R0。

根据图1可列出电流方程如下：

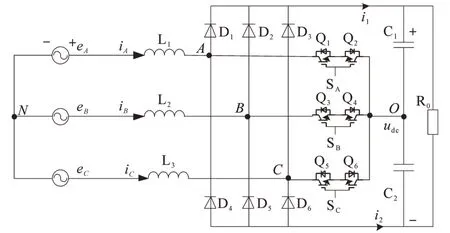
图1 三相三线VIENNA主电路拓扑Fig.1 Three-phase three-wire VIENNA main circuit topology

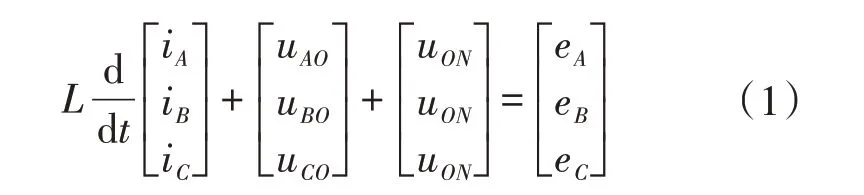
式中：uAO为A点到O点的电压，其余变量类似。

进行dq变换有：

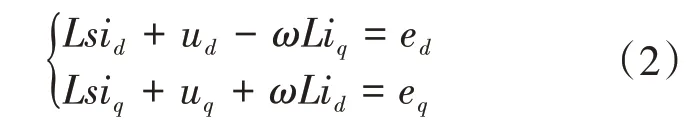
式中：id，iq和ud，uq分别为三相电流和电压在旋转坐标系下的变量。

列出电压方程如下[11]：

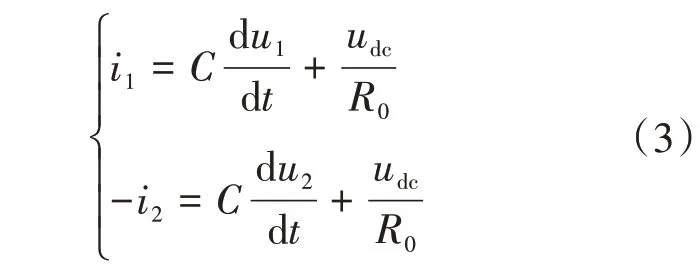
式中：u1，u2为上、下电容的电压值。

进行dq变换得：

基于系统模型的控制器设计可参考文献[11]等。

1.2 三电平空间矢量分布以及连续调制

令X表示A，B，C中的任意一相，当SX=1时对应相的反向串联开关管处于开通的状态，此时对应相的桥臂电压uXO=0；当SX=0时，对应相的反向串联开关管处于关断的状态，此时该桥臂输出电压取决于该相电流方向，当iX＞0，uXO=udc/2，当iX＜0，uXO=-udc/2。所以对于此系统，由于三相不同的开关组合可以得到27种电压组合，或者19种不同矢量（其中包含大、中、小、零矢量，共4类）。

VIENNA整流器的空间电压矢量[3]分布如图2所示。

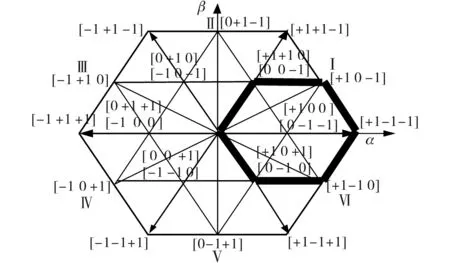
图2 VIENNA整流器电压矢量Fig.2 The voltage sector of the VIENNA rectifier

上述空间矢量图中，可以以0°角或α正轴为起点，以π/3为步长，划分出6个扇区。

表1列出了图2中粗实线所围区域内的电压矢量组合，其中三相驱动组合011和100分别对应小矢量[+1 0 0]和[0-1-1]，用来调节中点电位。

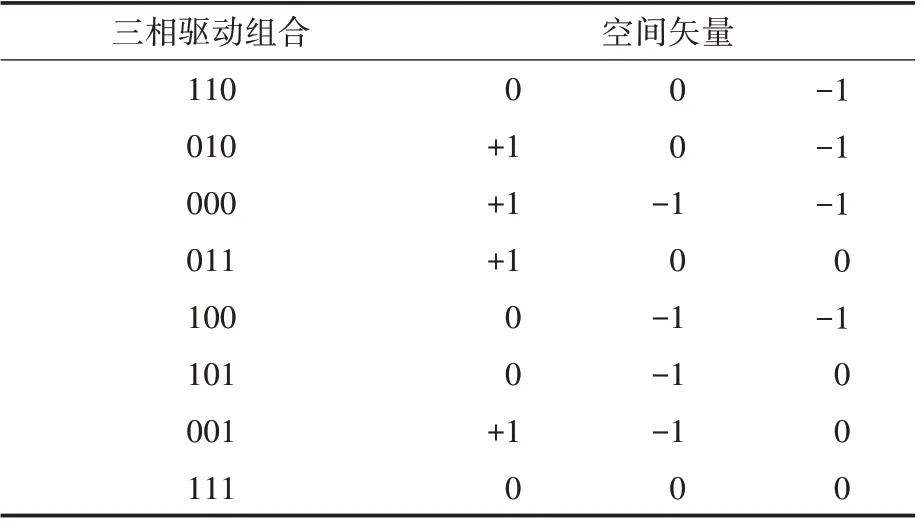
表1 粗实线所围区域内三相驱动组合和开关组合对照表Tab.1 Comparison table of three-phase drive combination and switch combination in the area enclosed by the thick solid line

传统的七段式SVPWM基本矢量作用顺序的分配原则是：在尽可能减少开关次数的条件下去降低PWM的谐波分量，所以在每次动作开关的时候，只改变其中一相的开关状态，并且对零矢量进行时间上的平均分配，使之能产生对称的PWM。通过对矢量的平移与两电平SVM等效，再使用两电平SVM的计算方式获得三电平有效矢量的作用时间，最后得到两电平扇区的矢量[3]。

考虑到VIENNA整流器各桥臂输出电压同该相电流有关（例如，当某相为正电流时，该相对应桥臂输出电压只有正或零电压），故可根据电流方向组合将图2划分出不同的区间，如图3所示。

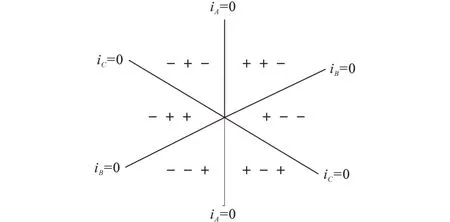
图3 以电流方向划分电压矢量空间Fig.3 Divide the voltage sector space by current direction

1.3 VIENNA整流器的中点平衡问题分析

在对直流侧中点电位平衡控制的研究中，常用方法是：由于小矢量对中点电位的作用相反，因此可以通过调整这2个矢量的相对时间来控制中点电位，对具体算法已有一些研究成果可供参考[12-13]，此处不再赘述。

2 三电平VIENNA整流器的断续调制

为提升系统效率，降低开关损耗，进一步研究VIENNA整流器的断续调制。

2.1 VIENNA整流器断续调制及中点电位控制

VIENNA整流器的断续调制与普通电平的调制类似，其断续调制要求在某一扇区内，A/B/C中的某一相保持开关状态不变。但与普通的三相全桥有所不同的是，各相的工作状态也有赖于当前时刻的电流方向，因此对断续调制的矢量选择形成了约束，这一点下文还将继续讨论。

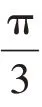
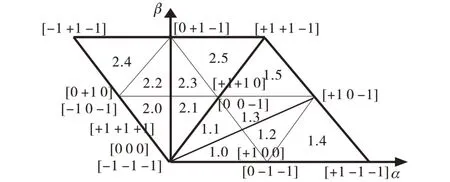
图4 第1和第2扇区Fig.4 The first and second sectors

根据各小区的矢量序列，设定某一相开关状态不变，不失一般性，得到第2扇区的断续调制开关组合方式如表2所示。

表2 断续式调制第2扇区的2种矢量组合方式Tab.2 Composition of vectors for discontinuous modulation in the 2nd sector

如表2所示，为实现各小区内的断续调制，同时也要考虑中点电位，最直观的做法是在每个扇区采用两种矢量组合方式，每种组合方式只使用1对冗余矢量中的1个，方式1表示给上电容充电的矢量组合方式，方式2表示给下电容充电的组合方式。

2.2 VIENNA整流器大电流不动作断续调制及中点电位控制

为了进一步降低VIENNA整流器的开关损耗，通常当某一相电流达到最大值附近时，控制该相对应开关管处于连续的高电平或低电平状态。

以图2中第2扇区为例进行分析，图5为2.4和2.5小区大电流不开关角度。若系统工作在单位功率因数下，当α-β坐标系下的控制量Uref如图5所示时（虚线箭头表示控制量Uref的轨迹），给定电压矢量会落在2.2/2.3/2.4/2.5小区。由图3可知，2.2和2.4小区B相电流最大，且为正；2.3和2.5小区C相电流最大，且为负。所以2.4小区应该采用方式1，但采用此方式在2.2小区无法实现最大电流不开通，从图4中可以看出，这是因为此时针对B相实现不开关的序列中必将包含向量[+1+1 0]，考虑图3中标示A相电流此时为负，根据VIENNA整流器的特点，该向量中的A相只能输出0或者-1，即[+1+1 0]向量无法实现。进一步，通过观察表2中2.2对应的2种开关组合方式可知，其方式1可以实现A相的断续调制，开关方式2可以实现C相的断续调制，尽管此时A相或C相非最大电流相，但也可以实现一定的效率提升。

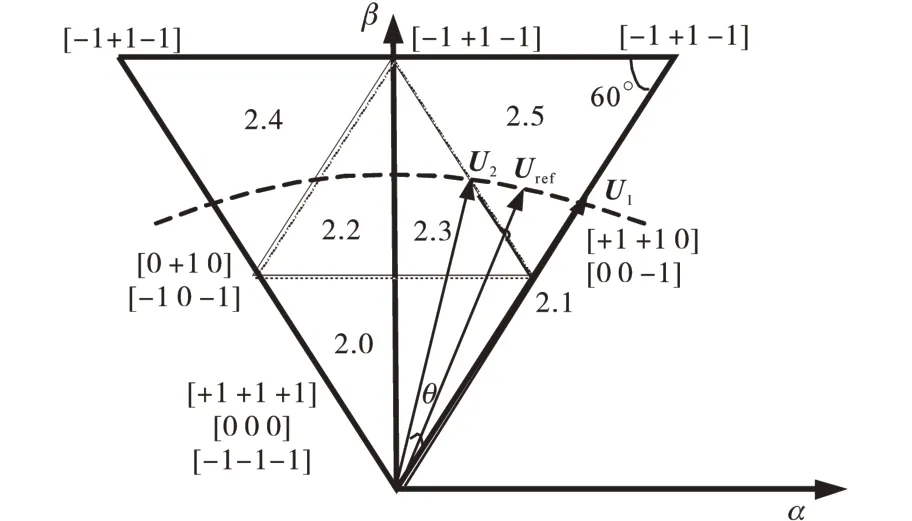
图5 2.4和2.5小区大电流不开关角度Fig.5 2.4 and 2.5 cell high current non-switching angle

为此，为了优化系统效率，如图5所示，在2.4小区内实现方式1的最大电流不开关，在2.5小区实现方式2的最大电流不开关。

进一步再考虑系统中点电位控制的问题，当给定电压矢量Uref落在2.5小区的边界时，对应矢量U1，U2，如图5所示，则在2.5小区大电流不开关的区域是(π/3,π/3+θ)，根据控制量的幅值M，再结合正余弦定理，即可求出θ的值，具体计算公式这里不再赘述。则在2.4和2.5小区内大电流不开关的角度为2θ。

为进一步提升效率，可以考虑在2.2/2.3内也实现某相的不开关。将图5进行细化，考虑到中点电位控制，引入变量Δ，如图6所示，其物理意义为进行中点电位控制时所需要的角度范围。在该角度范围内实现中点电位控制，当系统中点电位不平衡越大时，则需要该角度越大。而在该角度之外，则又可以将2.2和2.3区域进行如下处理：对2.2区域内且不包含在Δ之内的区域，采用表2中对应的方式1的调制办法；对2.3区域且不包含在Δ之内的区域，采用表2中对应的方式2的调制办法；而在Δ之内进行中点电位控制，选择方式1或者方式2。

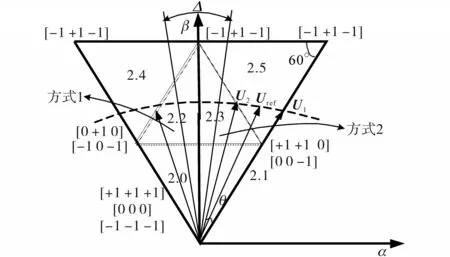
图6 2.2和2.3小区Fig.6 2.2 and 2.3 sectors

在上文基础上，结合大电流不开关断续调制，得到VIENNA整流器矢量控制系统如图7所示。

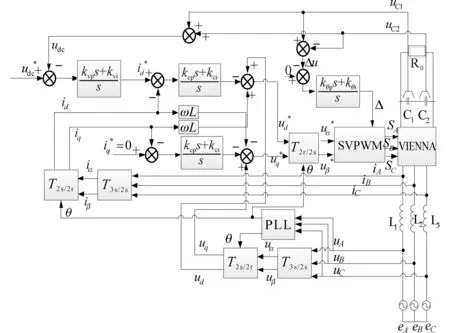
图7 VIENNA整流器矢量控制系统Fig.7 VIENNA rectifier vector control system

必须指出的是，在系统的控制中，只要中点电位在系统允许范围内，是可以允许有一定波动的，这样更有利于通过断续调制降低整流器整体的开关频率。

3 仿真及实验验证

在Matlab软件里搭建三相三线VIENNA整流器的拓扑，仿真验证本文研究的调制方法，参数设置如下：三相市电相电压220 V/50 Hz，开关频率19.2 kHz，直流侧电压600 V，直流侧电容C1=C2=900 μF，输出功率5 kW。图8为Simulink中搭建的仿真结构图。

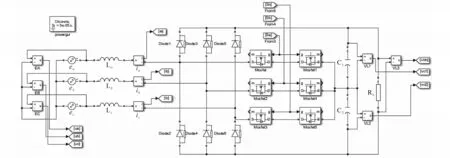
图8 仿真中搭建的VIENNA拓扑图Fig.8 VIENNA topology built in simulation

图9为C相电流和开关管的驱动波形SC，可看出C相电流处于峰值附近时，对应相的反向串联开关管不进行高频切换，从而实现了大电流不开关的断续调制，降低了开关损耗。

图9 C相电流和驱动波形Fig.9 Current and PWM waveforms of phase C

图10为直流母线电压、直流侧上下电容电压以及直流母线电压纹波的仿真波形。可以看出，直流侧上下电容的电压相等，直流母线电压的纹波范围在±15 V左右。

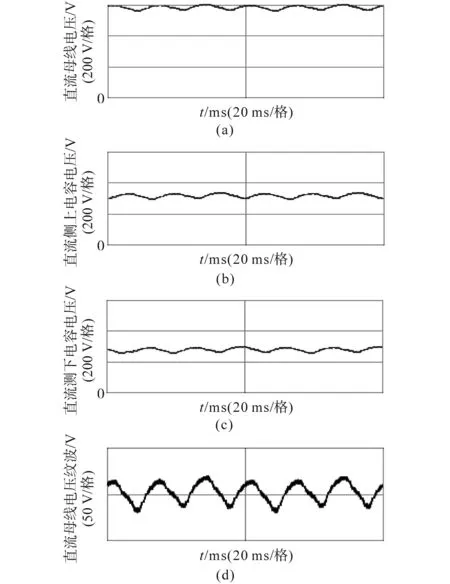
图10 直流母线电压、直流侧上下电容电压及纹波电压波形Fig.10 Waveforms of DC bus voltage，DC side upper and lower capacitor voltage and ripple voltage

搭建VIENNA整流器平台来进一步验证本文所提出的调制方法，控制板上采用TI公司的TMS320F2812作为主控制芯片；主功率开关器件采用K40T1202型号的IGBT；硬件电路参数与Matlab仿真参数相同。

图11为VIENNA整流器平台的输出电压纹波放大图，纹波幅值控制在15 V左右，尽管有一定的波动，但仍然是处于系统的允许范围之内。图12为C相驱动波形、C相电流以及输出直流电压波形，直流电压总体平滑稳定，流过C相的电流在达到电流最大值的附近时，该相的开关管不动作，故这种调制方式能在较大程度上提高系统的效率。

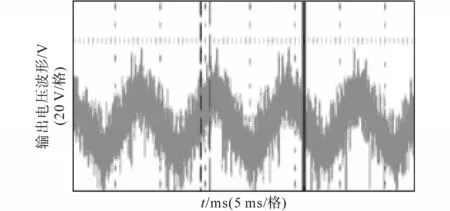
图11 VIENNA整流器输出电压纹波波形放大图Fig.11 The magnified waveform of VIENNA rectifier output voltage ripple

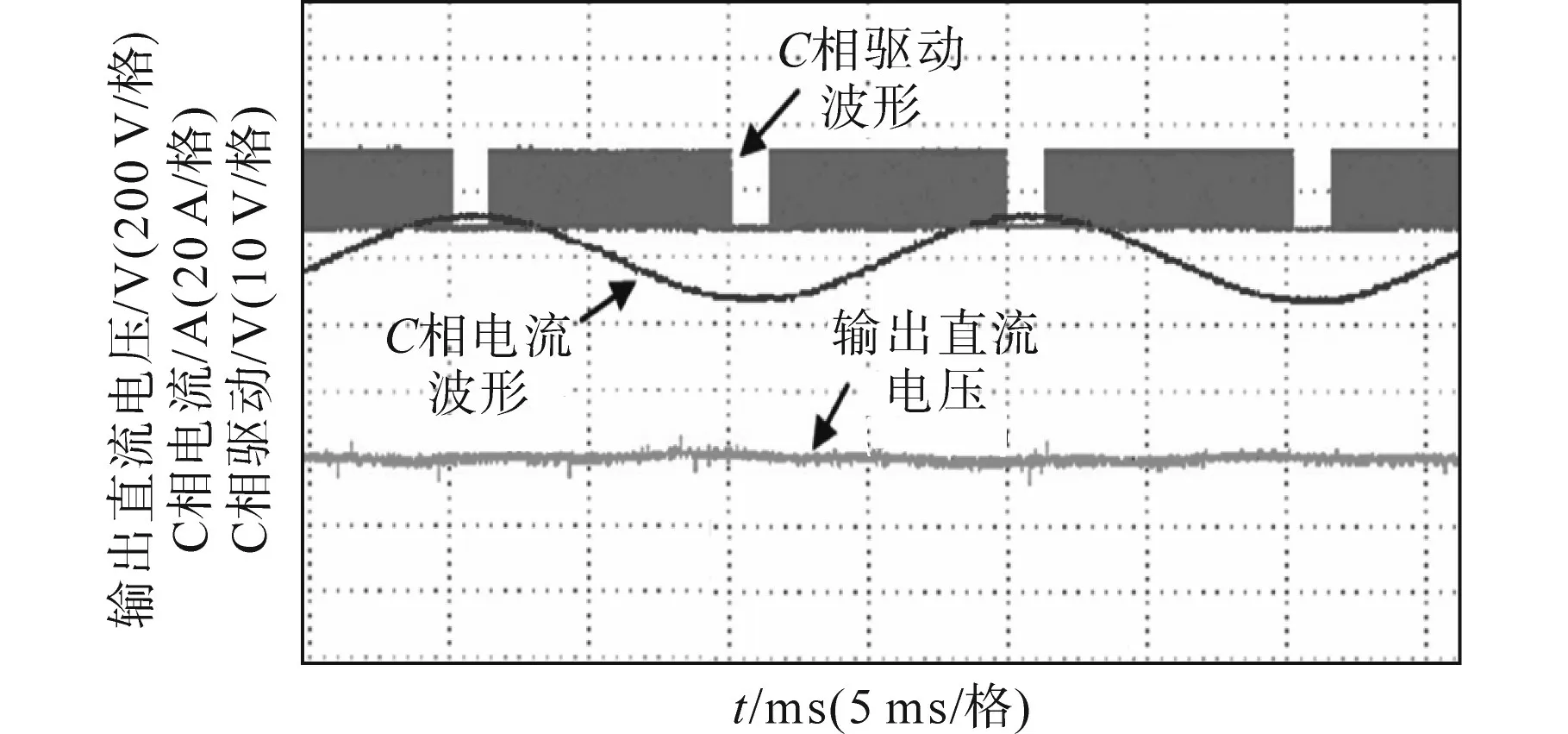
图12 VIENNA整流器C相输入电流以及对应的开关驱动波形Fig.12 Waveforms of VIENNA rectifier C-phase input current and corresponding switch drive

为了更加直观地验证本文所提出的这种调制方式对VIENNA整流器系统提升效率的作用，本文做了一组对比试验。效率对比如图13所示，其中，Po为输出功率。无差拍-DPWM调制是文献[8]采用的研究方法，大电流不开关断续调制是本文采用的研究方法。从图13中容易看出，在5种不同功率等级下，本文采用的大电流不开关断续调制的系统效率更高。

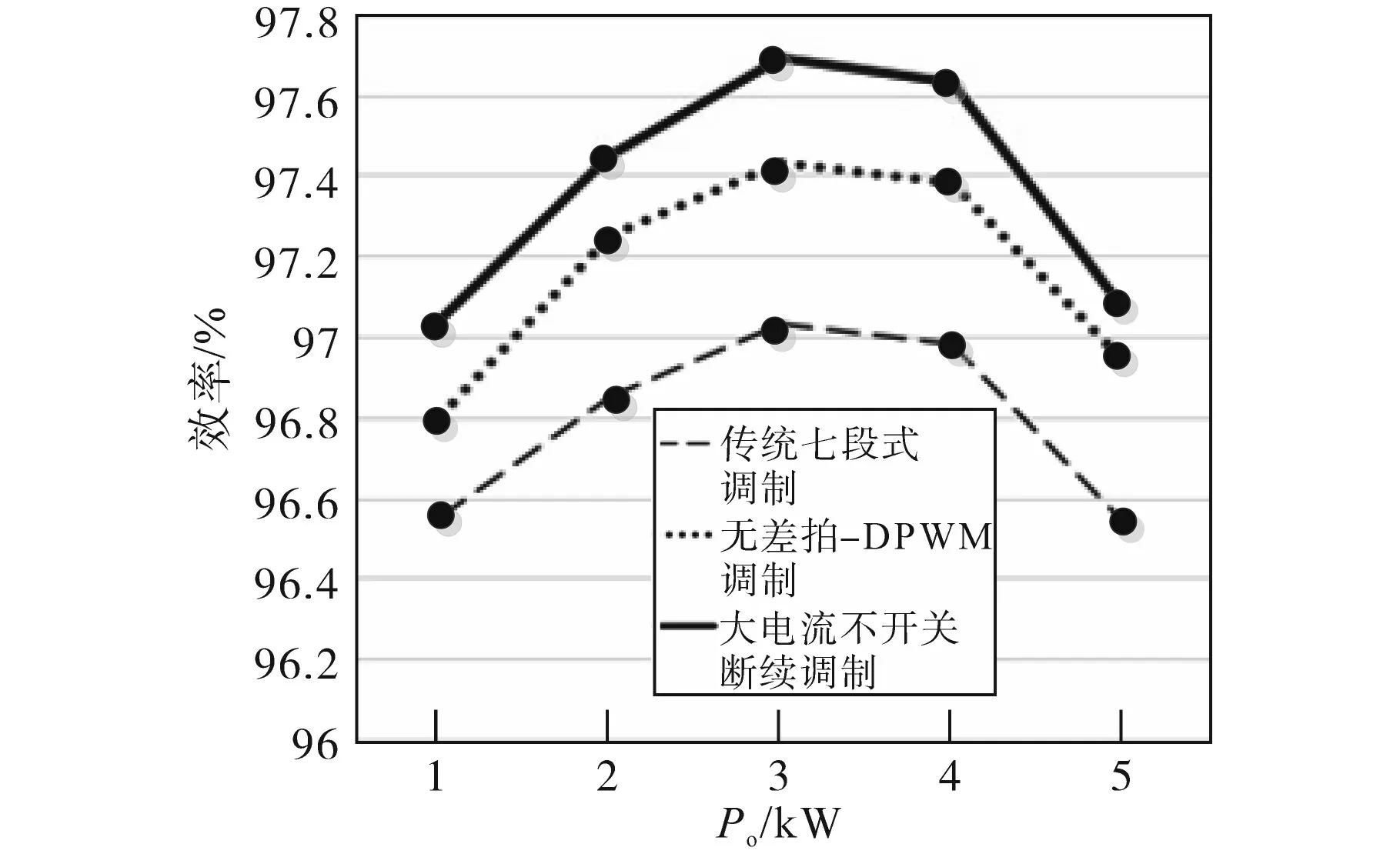
图13 效率对比Fig.13 Efficiency comparison

4 结论

本文主要提出了一种VIENNA整流器的断续调制算法，通过大电流的开关不动作可以提升系统效率。同时，本文还对断续调制时的中点电位控制技术进行了研究，并给出了相关的控制器，最终通过仿真和实验验证了所提调制算法和控制器的可行性。