Numerical Implementation of a Unified Viscoplastic Model for Considering Solder Joint Response under Board-Level Temperature Cycling

Hung-Chun Yang and Tz-Cheng Chiu

Department of Mechanical Engineering,National Cheng Kung University,Tainan,701,Taiwan

ABSTRACT An implicit integration scheme was developed for simulating the viscoplastic constitutive behavior of Sn3.0Ag0.5Cu solder and programmed into a user material subroutine of the finite element software ANSYS.The numerical procedure first solves the essential state variables by using a three-level iterative procedure,and updates the remaining stress and state variables accordingly.The numerical implementation was applied to consider the responses of solder joints in an electronic assembly under temperature cycling condition.The viscoplastic strain energy density accumulation over one temperature cycle was identified as a feasible parameter for evaluating the thermomechanical reliability of the solder joints.

KEYWORDS Pb-free; hysteresis; ratcheting; fatigue; tangent modulus

1 Introduction

In state-of-the-art microelectronic assemblies,the individual integrated-circuit (IC)components are connected to the printed-circuit board (PCB)through arrays of solder joints.Under service conditions involving repetitive temperature changes,the mismatch between the coefficients of thermal expansion (CTEs)of the PCB and IC components leads to thermomechanical fatigue and failure of the electronic assembly.The solder joint,which is the electrical as well as the structural interconnection between the component and PCB,is typically the weakest link from the perspective of thermomechanical reliability.Accurate prediction of the solder joint response is therefore imperative to the reliability modeling of the electronic assembly.In order to achieve that,the simulation should be able to consider the constitutive behavior of the solder under service conditions.One of the standard solder materials used in the board-level assembly is the Pb-free Sn3.0Ag0.5Cu (96.5 wt.% Sn,3.0 wt.% Ag,0.5 wt.% Cu)alloy which has a melting temperature of 217◦C.The homologous temperature of the Sn3.0Ag0.5Cu solder in typical system operating conditions is around or above 0.5.As a result,the solder joint exhibits significant time-dependent inelastic deformation during temperature cycling of the electronic assembly.An obvious choice of modeling the time-dependent inelastic behavior of solder is by using the state-variable based unified viscoplasticity approach [1,2].For considering the complex thermomechanical responses of lead free solders,some of the recent studies modified the Chaboche-model framework to incorporate features such as static recovery,temperature dependence and damage evolution [3–6].Rate-or temperature-dependent model parameters were also implemented in the McDowell-model and Anand-model frameworks [7–9] to consider the solder behavior under a wide range of strain rates and temperatures.

The mathematical form of the unified viscoplastic model is typically a set of nonlinear first-order differential equations,and the corresponding thermomechanical problem is solved by using nonlinear finite element (FE)procedure.In the FE procedure for analyzing the viscoplastic problem,the stress equilibrium is expressed in the form of nonlinear virtual work equations.The process of obtaining the nodal displacements involves applying the load in a sequence of discrete time steps and solving the global nonlinear equilibrium equations at each incremental step by Newton-Raphson iteration.During each global equilibrium iteration,values of new stresses and internal state variables at each Gaussian integration points are calculated for the prescribed strain increment and temperature change.These results are then used to determine the residual force vector and the material tangent stiffness for the FE stiffness matrix.The calculations of the new stresses and state variables at Gaussian integration points are performed with a time-integration scheme of the viscoplastic model.In the integration scheme,the coupled and nonlinear differential constitutive equations are discretized in a strain-driven format.Time-integration procedures based on non-iterative forward-Euler scheme had been adopted for the viscoplastic model due to their easy implementation [10,11].A disadvantage of the explicit scheme is that the time increment is severely restricted because of numerical stability requirements.To overcome this issue,semiimplicit time-integration schemes were developed to improve stability and to retain numerical simplicity.These semi-implicit procedures [12–14] calculate the forward gradient of the relevant constitutive function by using Taylor series expansion at the initial state.These semi-implicit approaches are non-iterative and provide improvements over the explicit procedures.However,it is still important to control the time increment carefully because the accuracy of the forward gradient method may be severely affected by the time step size,especially in rapid-changing deformation regimes [14].Fu et al.[15] developed another semi-implicit time-integration approach.In this procedure,the effective viscoplastic strain increment is evaluated by using real implicit integration method while the other state variables are obtained by explicit update.Similar approach was adopted to address the integration problem for a damage-coupled unified viscoplastic model [16].

Fully-implicit backward Euler schemes had also been implemented in time-integration procedures for viscoplastic models [17–27].Because of the unconditional stability in time step size,it is possible to improve the computational efficiency of these schemes without much loss in solution accuracy.In the implicit scheme,nonlinear equations of the new stress and other state variables are derived from the constitutive equations,and then transformed to a set of nonlinear algebraic equations of the unknown variables.Iterative procedures were usually applied to solve the system of nonlinear equations.Because the iterative solutions are performed at every Gaussian integration point for each time step,the computation cost would be very significant if the number of unknowns is higher than the essentially independent variables in the constitutive model,especially when tensor-valued internal state variables are used [17,18].For improving the computation efficiency,efforts had been focused on simplifying the discretized nonlinear system of equations such that the number of unknowns is reduced to the same as the number of independent variables in the corresponding constitutive model [19–25,27].Hartmann et al.[19,20] showed that,for plastic and viscoplastic models with multiple Armstrong-Frederick kinematic hardening terms,the nonlinear system of equations can be reduced to one scalar nonlinear equation for calculating the new state variables.By following a similar derivation,Kobayashi et al.[21] demonstrated that the implicit integration of kinematic-hardening plastic model consisting strain hardening and dynamic recovery terms can also be reduced to solving a scalar nonlinear equation.The approach was also applied to reduce the number of equations for more complicated constitutive models [22–24].

Aside from the discretized form of the constitutive equations,the robustness of the numerical solution is also influenced by the iterative procedure.In general,Newton-Raphson iteration can readily be adopted for solving the equations.However,for handling equations of high nonlinearity,designs of appropriate local iterative schemes were proposed [18,21,22,24–26].Saleeb et al.[18]applied line-search strategy to improve the robustness of the Newton-Raphson iterative solution.Kobayashi and coworkers adopted a successive substitution method for solving nonlinear scalar constitutive equations [21,22].Multi-level iteration strategies were also adopted for solving the discretized nonlinear constitutive equations:Kullig et al.[24] presented a two-level iteration strategy by combing Pegasus method and fixed-point iteration to solve a system of three coupled nonlinear equations,Lush et al.[25] developed a two-level iteration strategy that combines the Newton-Raphson procedure with bracketing method for obtaining good global convergence.

In this paper,a fully-implicit time-integration scheme is presented for a novel viscoplastic constitutive model of Sn3.0Ag0.5Cu solder [6].The viscoplastic model,which was proposed by the authors of this paper,was first discretized and reduced to a set of four coupled nonlinear zero-form equations for the four essentially independent variables.A multi-level iteration strategy was implemented for solving this set of nonlinear equations.The implicit integration scheme was programmed for the user-defined material subroutine USERMAT in commercial FE software ANSYS [28] to perform local computation.For each current load step in the global equilibrium iteration,new local stress and state variables at every Gaussian integration point are calculated from the given strain and temperature increments.Furthermore,the consistent tangent stiffness was also derived and programmed into the USERMAT.It is used for preserving the quadratic convergence of the global Newton–Raphson equilibrium iteration [29,30].The FE simulations of solder bar under strain- or stress-controlled uniaxial cyclic loadings were conducted in ANSYS with the USERMAT subroutine,and compared to experimental results for validating the implementation.The USERMAT subroutine is also applied to consider the thermomechanical responses of the ball grid array (BGA)Sn3.0Ag0.5Cu solder joints in an electronic assembly under temperature-cycling reliability test condition.

2 The Constitutive Model

From experimental characterizations under monotonic and cyclic loading conditions,a kinematic hardening rule based viscoplastic model was developed for the Sn3.0Ag0.5Cu alloy [6].The main features incorporated in the model include dynamic recovery function for considering cyclic softening and static recovery term for considering relaxation under monotonic loading.A brief description of the constitutive model is given in this section.

Within the framework of unified viscoplasticity,the strain tensor can be expressed as

whereαis the CTE andT0is the reference temperature of zero thermal strain.

The flow equation of the unified viscoplastic model is given by

where ˙pandare the viscoplastic strain rate norm and the viscoplastic normal tensor,respectively,and are given by

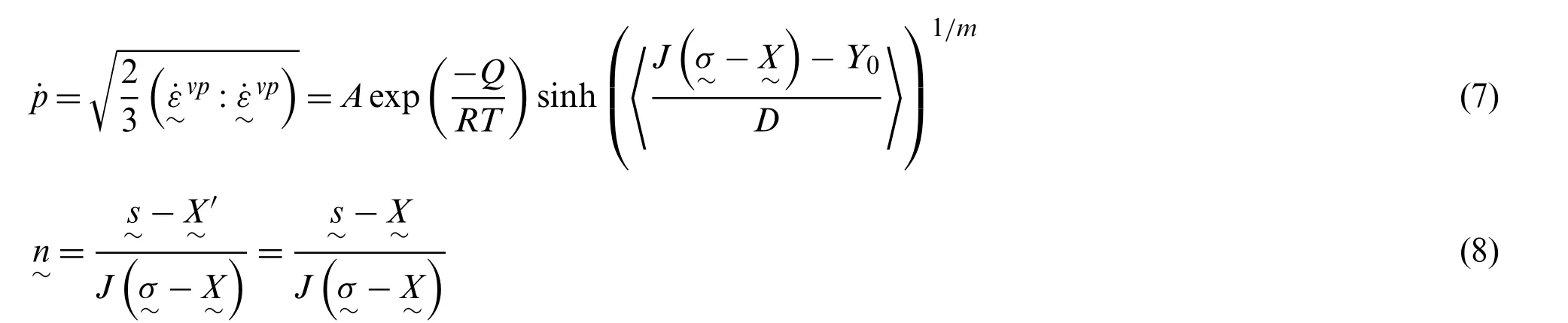
In Eq.(7),A,D,m,Q/RandY0are material parameters,is the back stress tensor for which the trace is zero,is the von-Mises invariant of the effective stress,the Macaulay brackets,〈〉,is defined as 〈x〉=(x+|x|)/2.In Eq.(8),is the deviatoric back stress tensor,and the effective deviatoric stress,,also gives the direction of the viscoplastic strain rate.Because the trace of the back stress tensor is zero,it is such that.

The internal state variable of the viscoplastic model is the back stress,,which consists two components,i.e.,

whereCi,di,andmiare the material parameters,JX,iis the second invariant of the back stress tensor,γiis the dynamic recovery parameter and is a function of the viscoplastic strain norm,p,and the radius of the strain memory surface,q.For considering the cyclic-softening behavior of the material,γiis modeled as

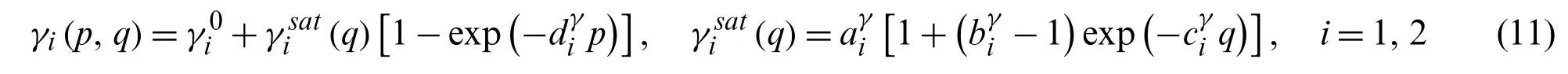
whereηis a material parameter,H()is the Heaviside step function (H(x)= 1 ifx≥0,H(x)=0 ifx<0),andare the unit normal tensors of the viscoplastic folw and the strain memory surface,respectively,and are given by

The unified viscoplastic model described in Eqs.(6)–(15)consists 22 material parameters:A,Q/R,D,m,Y0,ηand,i= 1,2.A summary of the these material parameters for Sn3.0Ag0.5Cu solder is given in Tab.1.The model was validated through comparing the numerical results to experimental solder responses under constant strain-rate,creep and creep-relaxation conditions at constant temperatures between 25 and 150◦C [6].Note that the viscoplastic model described in Eqs.(6)–(15)is a phenomenological model.The back stress evolution equation is used for modeling the macroscopic response associated to the competition between the hardening and recovery effects of the microstructure.A micromechanics based multi-scale physical model would be more suited for considering the influence of grain rotation,subdivision and local fractures in the material.

Table 1:The unified viscoplastic material parameters of the Sn3.0Ag0.5Cu (T in K)[6]

3 Numerical Implementation

The unified viscoplastic model described in Section 2 is discretized for numerical FE implementation by using an implicit backward-Euler integration scheme.Details of the time discretization,the numerical integration procedure,the approach for solving the nonlinear algebraic equations and the formulation of the consistent tangent modulus are given as follows.

3.1 Backward Euler Integration Scheme

In the FE procedure,the viscoplastic model,given as a system of nonlinear first-order differential equations,is integrated for a prescribed strain increment to update the stresses and state variables at the Gaussian integration points by using the implicit backward-Euler integration scheme.In this scheme,the time discretization of a general first-order differential equation=f (y,t)can be written as

where the subscriptsnandn+1 indicate the values of the variablesyat the start- and end-points of the time stepΔt.The unknown value ofyn+1can be obtained by an iterative procedure for the implicit Eq.(16).For simplifying the presentation of the discretized constitutive equations,ynandyn+1are replaced by ˆyandy,respectively,in the subsequent formulation.

Given that the stresses and state variables are known at timetn,the stress increment for a prescribed strain increment can be calculated from the discretized form of Eq.(4),given by

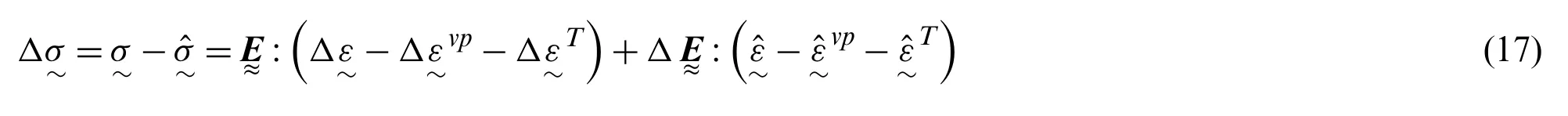
It is emphasized in Eq.(17)thatshould be considered as temperature dependent under anisothermal loading conditions.The assumption of incompressibility in viscoplastic deformation gives,and Eq.(17)can be rewritten as

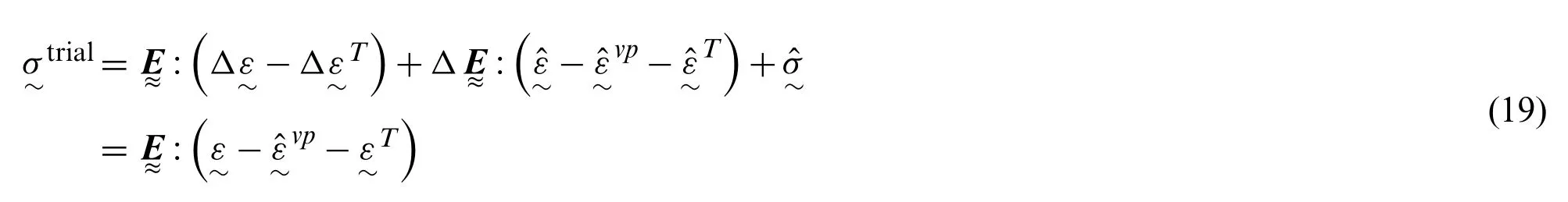
Eq.(18)leads to a predictor-corrector approach which is also known as the return mapping method [32,33].In this approach,the stress is first estimated by the trial stress,which is calculated by substituting the prescribedinto Eq.(19),and then updated through viscoplastic correction by the term.By decomposing the stress tensor in Eq.(18)into the hydrostatic and deviatoric parts and using the assumption of viscoplastic incompressibility,the hydrostatic and deviatoric stress tensors are given,respectively,by

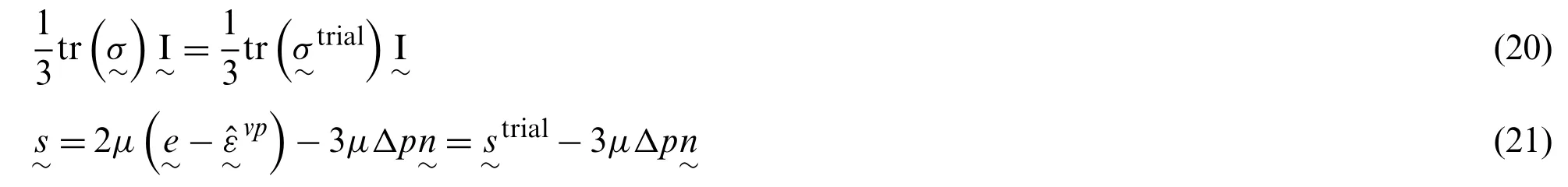
The discretization of the viscoplastic model in the backward-Euler form is given as follows.The discretized flow equations corresponding to Eqs.(6)–(8)are given by

The discretized back stress equation corresponding to Eq.(10)is given by

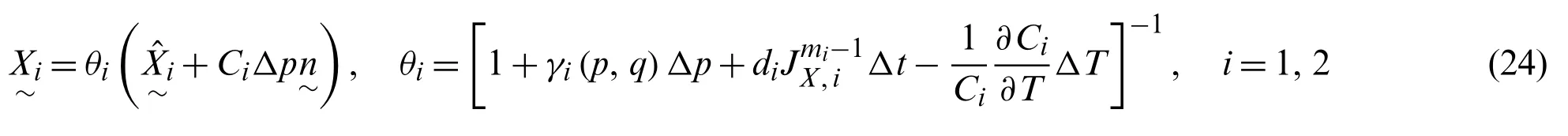
The evolution equation of the dynamic recovery parameter corresponding to Eq.(11)is given by

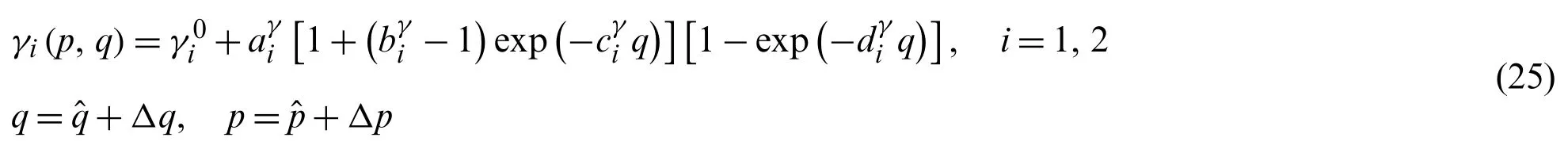
The strain-memory-surface related evolution equations corresponding to Eqs.(13)and (14)are given by

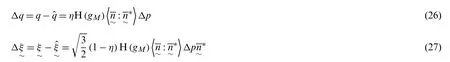
The discretization of the constitutive equations leads to a set of 26 unknowns:andThe implicit time integration scheme involves solving these 26 unknowns from a system of 26 simultaneous nonlinear equations given by Eqs.(21),(23),(24),(26)and (27).For simplifying the solution process,the discretized equations were reformed to reduce the number of unknowns.First,from Eq.(23),the von-Mises invariant of the effective stress can be written as a function ofΔp,given by

The effective stress at the new state can be obtained from Eqs.(21)and (24),and is given by

whereβandare both functions ofΔp,JX,1,JX,2,Δq,and are given,respectively,by

Eq.(29)can be converted to a scalar equation by calculating the von-Mises invariant of the effective stress tensor [20,24],which is given by

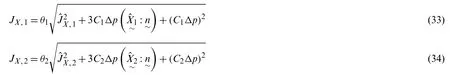
An additional equation forΔp,JX,1,JX,2andΔqcan be obtained from the strain memory surface Eq.(12),which requiresΔqandto satisfy

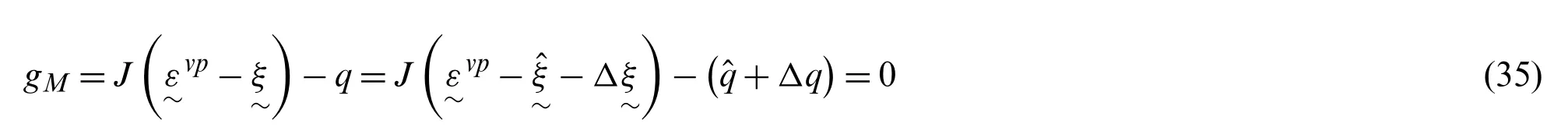
It can be seen from Eq.(35)thatqequals toBy substituting this equivalence and Eq.(26)into Eq.(27),Δ∼ξcan be expressed explicitly in terms ofΔqandgiven by

By substituting Eq.(36)into Eq.(35)and through some algebraic manipulations,it can be shown that

A nonlinear algebraic system consisted of four essential zero-form scalar equations forΔp,JX,1,JX,2andΔqcan be assembled by rewriting Eqs.(32)–(34)and (37),respectively,as

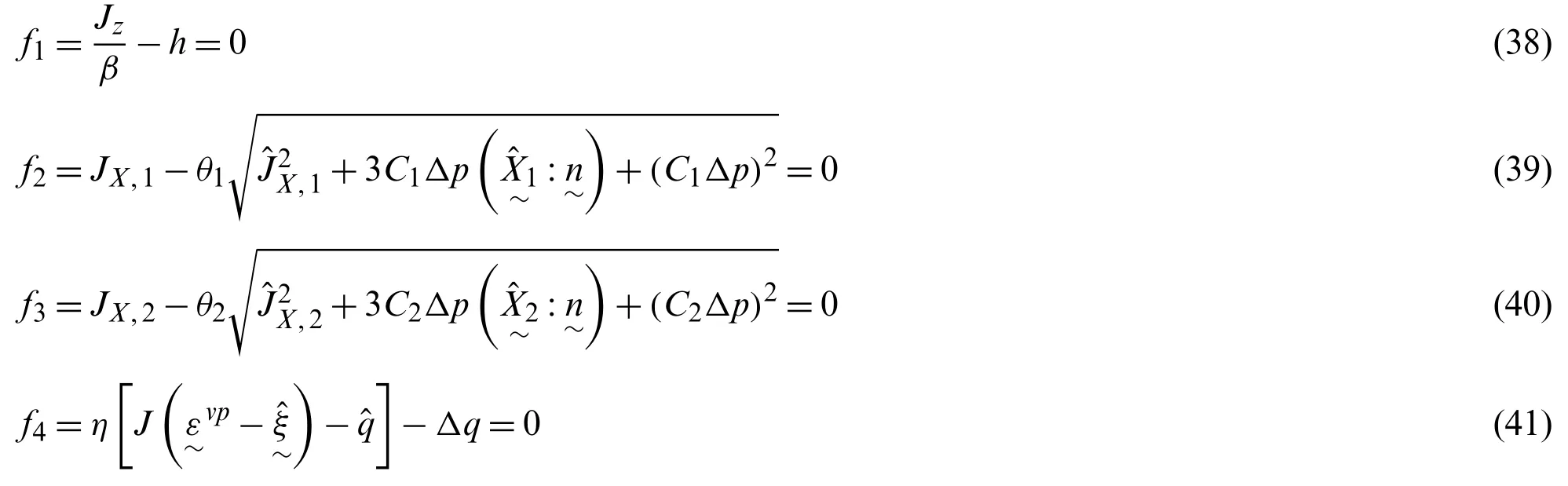
The evaluations of the 26 unknownsΔqandinvolve solving the four essentially independent variables (Δp,JX,1,JX,2andΔq)from the residual Eqs.(38)–(41)and then calculatingandfrom these four independent variables.

3.2 The Time-Integration Procedure

The flow chart of the time-integration procedure is shown in Fig.1.The time-integration procedure is used for calculating the stresses,strains,viscoplastic strains and other state variables at timetn+1from the known values at timetnand the incremental time,strain and temperature steps.In this procedure,the trial stressesandare first calculated for the givenandΔTby using Eqs.(19)and (21),respectively.

The second step in the time-integration procedure is to update the back stresses for the assumed purely elastic state.Under the assumed elastic state,the viscoplastic strain norm increment,Δp,and the strain memory surface radius increment,Δq,are both zero.Therefore,in the four independent variables required for updating stresses and other state variables,onlyJX,1andJX,2remain to be solved.It is worthwhile to note that,even under purely elastic increment,the back stresses may change because the static recovery and temperature dependence terms are present in the back stress evolution Eq.(10).Under the assumed purely elastic state,the discretized back stress equation can be simplified from Eq.(24)to

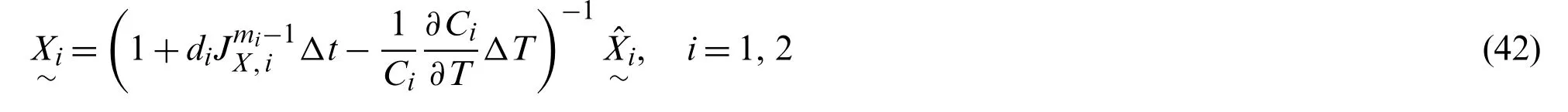
The zero-form equations that are used for solvingJX,1andJX,2for the assumed elastic state can be simplified from Eqs.(39)and (40)withΔp=0,and are given by

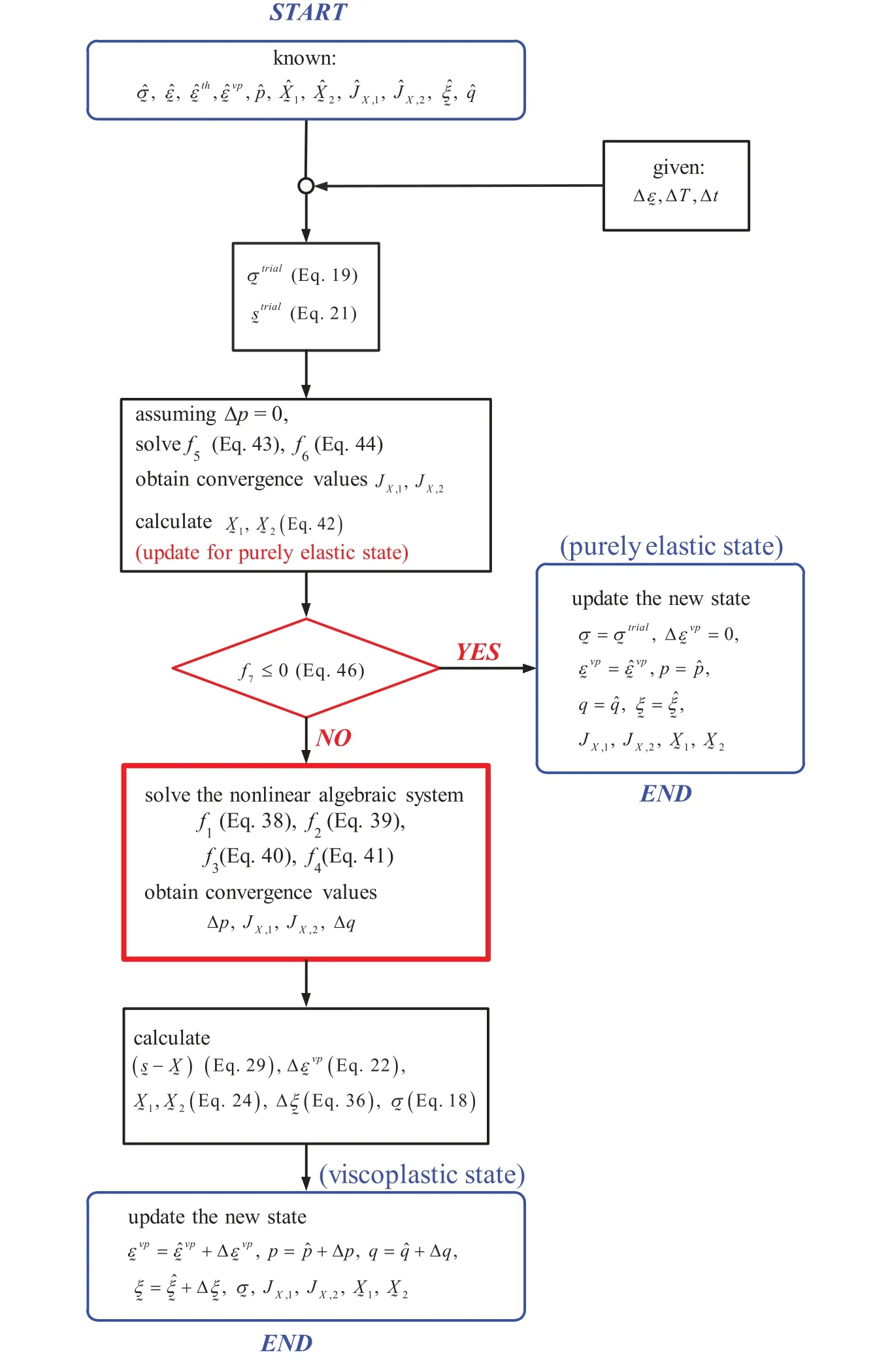
Figure 1:The time-integration procedure

The solutions of Eqs.(43)and (44)can be obtained by using the Newton-Raphson method.In this iterative procedure,initial guesses ofJX,1andJX,2for the case ofΔp=0 were determined by following the approach of Kullig et al.[24],and are given by

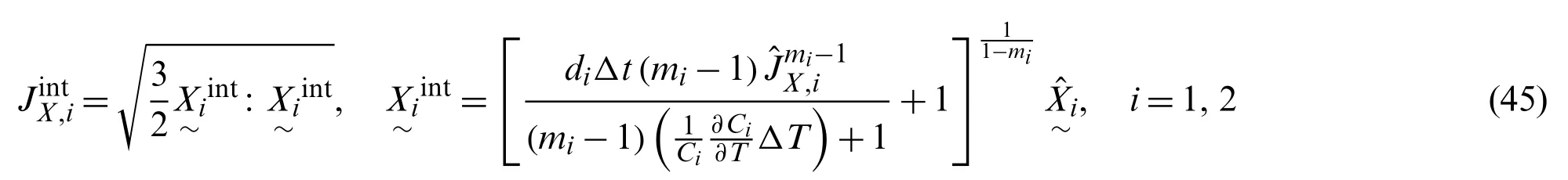
where the superscript “int” denotes the initial guess.OnceJX,1andJX,2are solved,the new back stresses can be calculated by using Eq.(42).The trial stress solutions are subsequently checked with the von-Mises yield criterion given by

3.3 Solution of the Nonlinear Algebraic System

Among the 4 unknowns to be solved from the simultaneous Eqs.(38)–(41),the orders ofJX,1andJX,2are much higher than those ofΔpandΔq.Furthermore,the flow equation related zeroform equation,Eq.(38),has high nonlinearity.Consequently,the application of standard Newton-Raphson procedure for solving the nonlinear system is prone to convergence issue.To overcome this issue,a three-level iterative scheme as shown in Fig.2 is developed by following the multi-level iteration strategy proposed by Kullig et al.[24].As shown in Fig.2,the global loop of the threelevel scheme,which is denoted as Level-1 iteration,operates to solve Eq.(38)forΔpby using the Pegasus method [34].The Pegasus method is one of the regula-falsi methods for obtaining the root of a nonlinear equation between prescribed lower and upper bounds.A natural lowerbound value ofΔpis zero,which corresponds to the purely elastic state.From the discussion in Section 3.2,it can be seen that Eq.(38)reduces to Eq.(46)whenΔp=0,and that the residual function evaluation would result inf1(Δp=0)=f7>0 when viscoplastic response is present.The upper-bound forΔpis selected from one of the two estimates given by

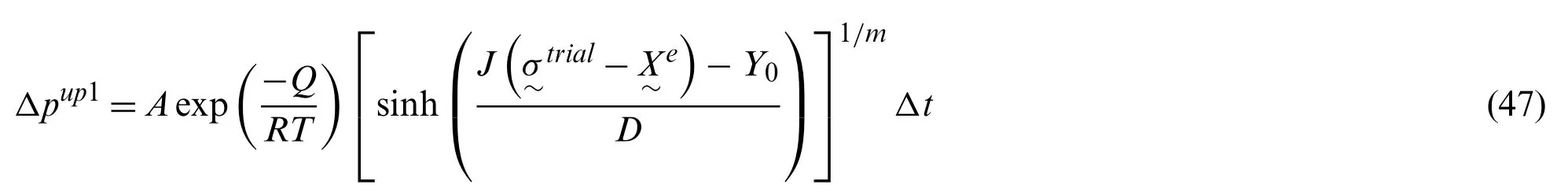
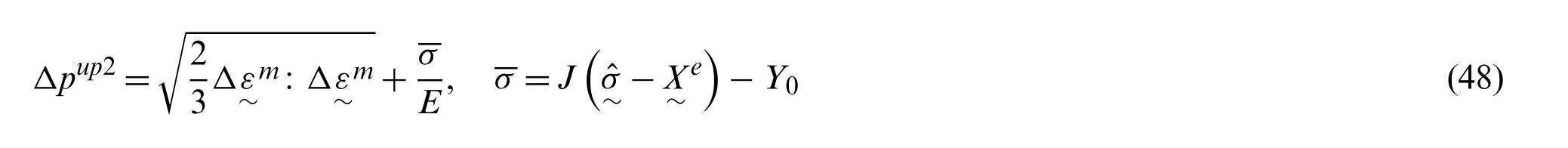
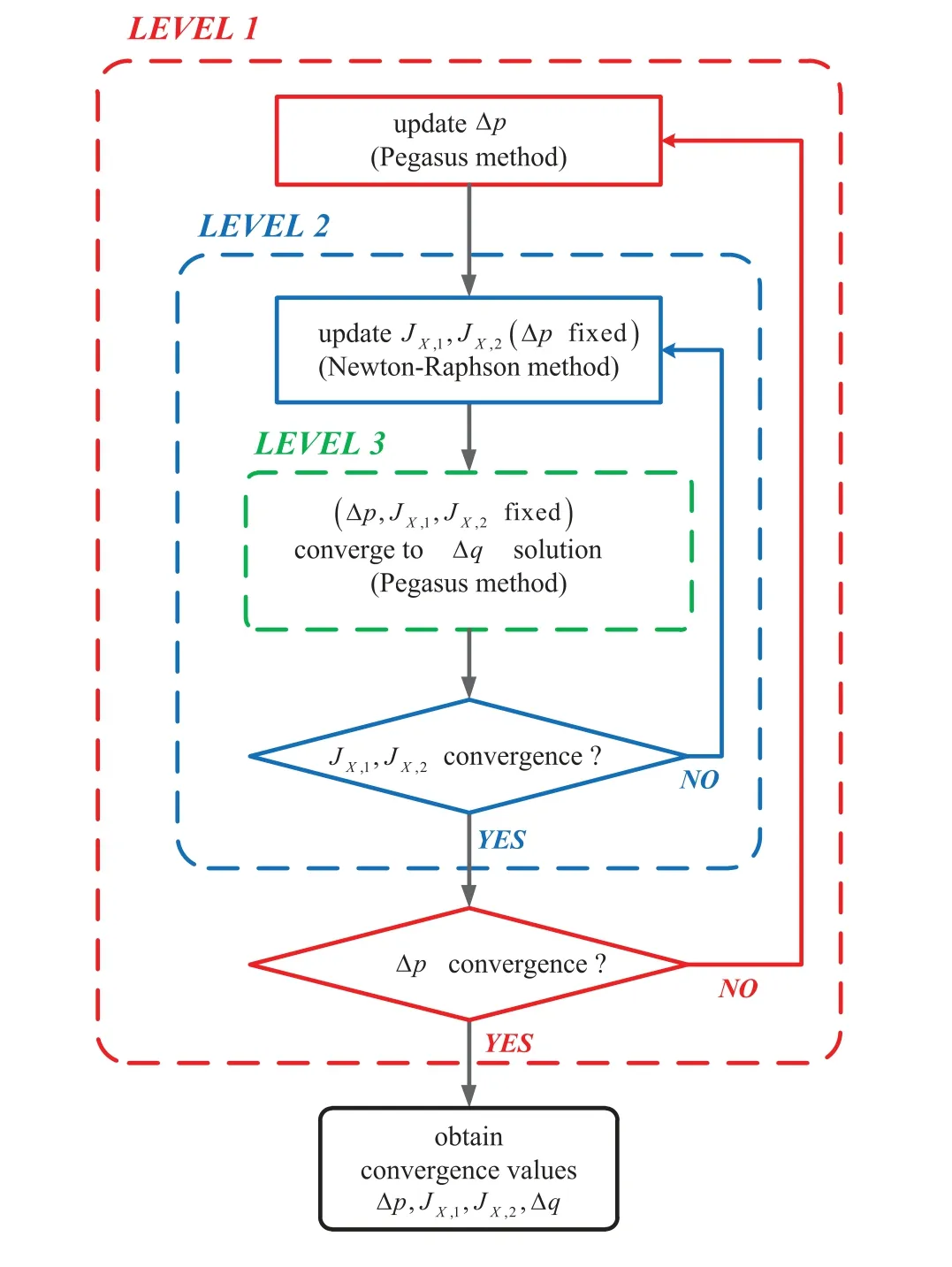
Figure 2:The multi-level iteration scheme

For each Level-1 iteration of evaluatingf1and updatingΔp,the remaining three unknowns(JX,1,JX,2,Δq)are calculated in the Level-2 and Level-3 iterations,as shown in Fig.2.In the second-layer (Level-2)iterative loop,Eqs.(39)and (40)are solved by using the Newton–Raphson method to determineJX,1andJX,2.After each Level-2 iteration of updatingJX,1andJX,2,the solution process enters into the third-layer (Level-3)loop to estimateΔq.The solution process evaluates Eq.(41)withΔpvalue (estimated in Level-1)andJX,1andJX,2values (estimated in Level-2)by using the Pegasus method.In the Pegasus method,the natural bound ofΔq=0 is selected as the lower bound for the iterative procedure.It can be shown that,whenΔq=0,=0 and Eq.(41)reduces to

Eq.(49)is expected to have a value greater than zero whenΔq>0.The upper bound ofΔqis selected to be the same as the value ofΔp,which results inf4<0 in the zero-form function evaluation.

Once the Level-3 iterative solution forΔqis converged,the process returns to Level-2 to check if the updated values ofJX,1andJX,2have reached convergence.If convergence is not reached,the Newton-Raphson iteration continues to updateJX,1andJX,2,together with the Level-3 iterative solution forΔq.IfJX,1orJX,2fails to converge in the Level-2 iteration,it implies that the given step sizeis too large,and the step size is reduced subsequently until the convergence is reached.Reducing the step-size could be achieved directly by using thekeycutcommand built in the USERMAT subroutine.After the solutions ofJX,1,JX,2andΔqreach convergence,the process returns to Level-1 iteration to updateΔp.The multi-level process continues untilΔpconvergence is reached.

For the iterative solution at each level iteration,it is considered as converged if the following condition is met:

whereyrepresents the variable to be solved,the subscriptkdenotes the number of the current iteration.

3.4 Consistent Tangent Modulus

The consistent tangent moduli are typically used in nonlinear FE procedures to preserve the rate of convergence in the Newton-Raphson solution for the global equilibrium equations in nonlinear problems.However,it does not affect the accuracy of the global iterative solution [30].The consistent tangent modulus is obtained by linearizing the stress expression with respect to the mechanical strain increment.In this study,derivation of the consistent tangent modulus is conducted by following the procedures proposed by Kobayashi et al.[22] and Akamatsu et al.[27].In the derivation,the differentials of the viscoplastic strain increment and the back stress are first expressed,respectively,as

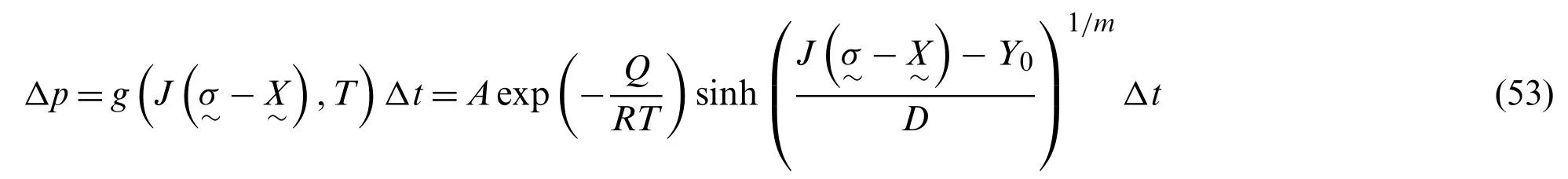
wheregis a function of the von-Mises invariant of the effective stress and temperature.Because the temperature is prescribed as the input in the time-integration procedure,the differential ofΔpcan be subsequently expressed as

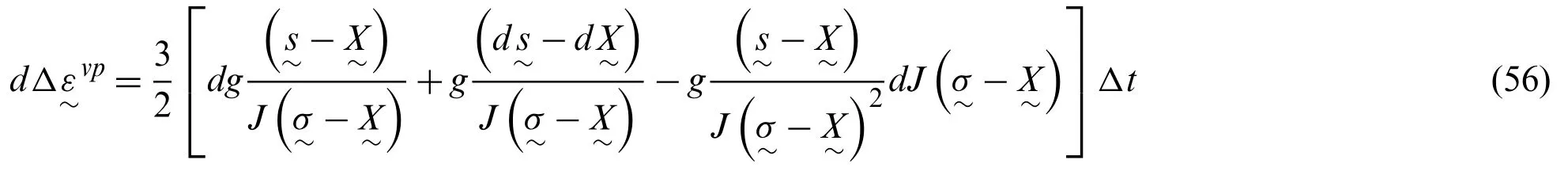
From Eqs.(51)and (56),it can be shown that

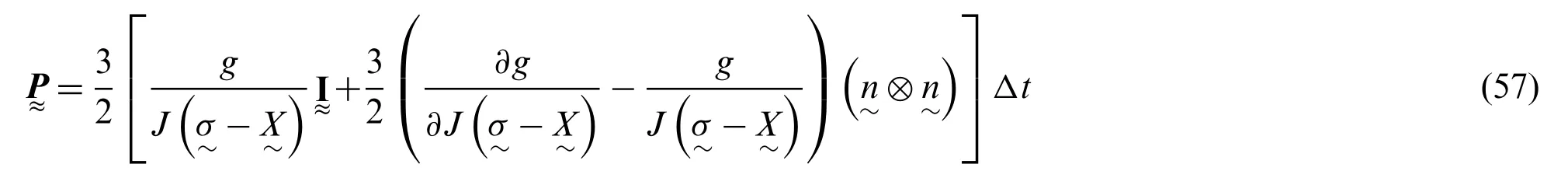
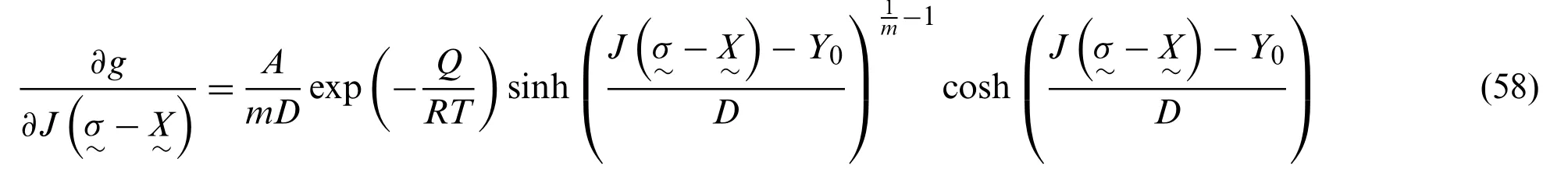
where

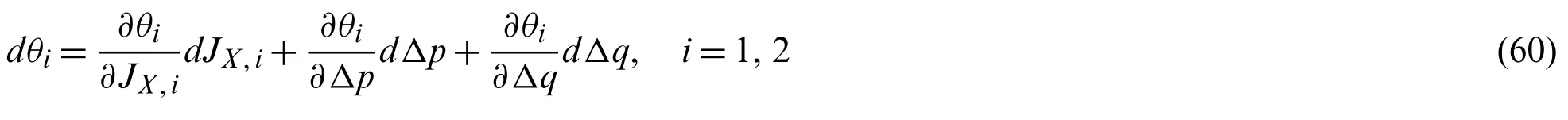
In Eq.(60),dJX,ianddΔpare given,respectively,by

The differentialdΔqin Eq.(60)can be obtained from Eq.(37),and is given by

By comparing Eqs.(52)and (59),it can be shown that

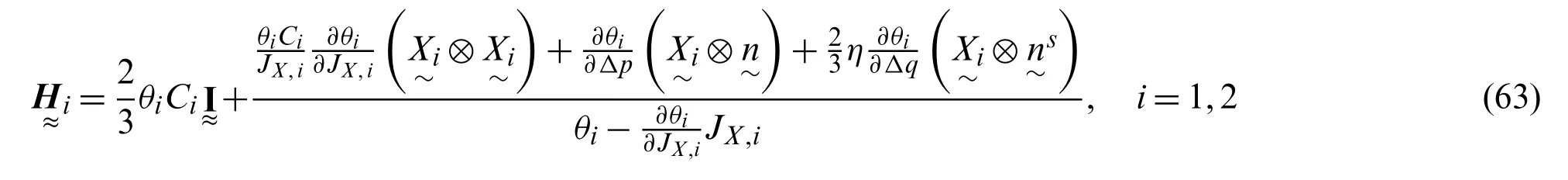
where∂θi/∂JX,i,∂θi/∂Δpand∂θi/∂Δqare given by

The∂γi/∂Δpin Eq.(65)and∂γi/∂Δqin Eq.(66)are given,respectively,by

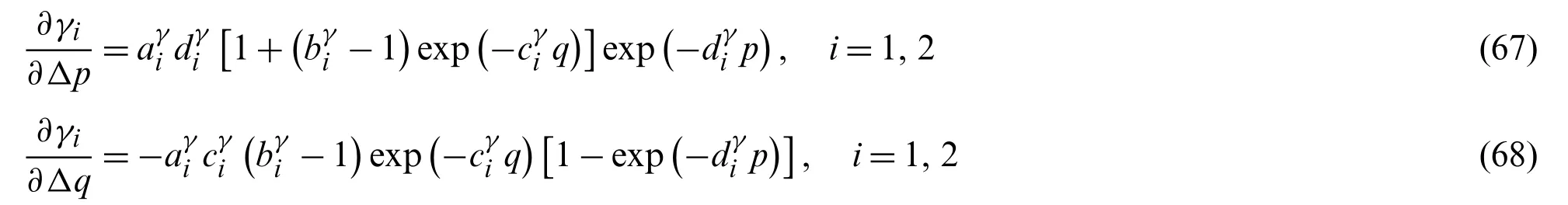
By substituting Eq.(52)into Eq.(51)and rearranging,it gives

From Eqs.(18)and (19),the differential stress can be expressed as

The deviatoric part of the differential stress can be expressed as

By substituting Eq.(72)into Eq.(69),the differential viscoplastic strain increment can be expressed as

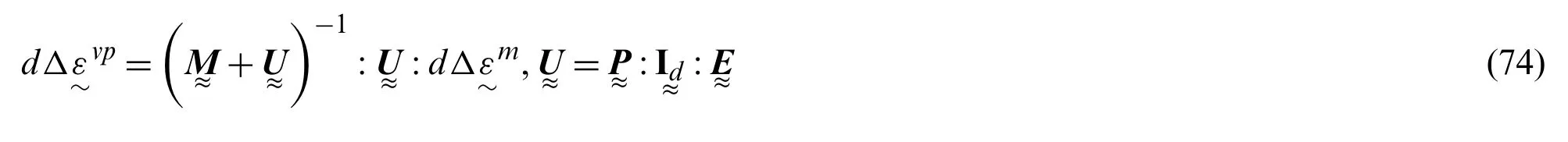
By further substituting Eq.(74)into Eq.(70),the consistent tangent modulus can be written as

4 Finite Element Results

The time-integration scheme and the consistent tangent modulus of the viscoplastic constitutive model was implemented as a USERMAT subroutine in the FEM software ANSYS.Numerical results of the Sn3.0Ag0.5Cu solder rod under cyclic loadings were first obtained and validated to the experimental data.The numerical model is then applied to simulate the responses of BGA solder joints under temperature cycling condition.

4.1 Solder Rod under Mechanical Cycling

The responses of Sn3.0Ag0.5Cu solder rod under uniaxial cyclic loadings at constant temperatures of 25,75 or 125◦C were considered by using FE simulations and compared to experimental results.The cyclic experiments were conducted on dog-bone shaped as-cast Sn3.0Ag0.5Cu specimens in an Instron 5565 tester.The cyclic loading was measured by using either a 500-N or 5-kN load cell,and the deformation was measured by using a dynamic extensometer.The finite element model,as shown in Fig.3,considers 1/8 of the gauge-length section with symmetric boundary conditions assigned on the 3 corresponding faces.The FE model has an overall dimension of 2.5 mm × 2.5 mm × 10 mm,and is meshed with 500 8-noded brick (solid 185)elements.The viscoplastic model parameters and the elastic constants of the Sn3.0Ag0.5Cu solder are given in Tabs.1 and 2,respectively.

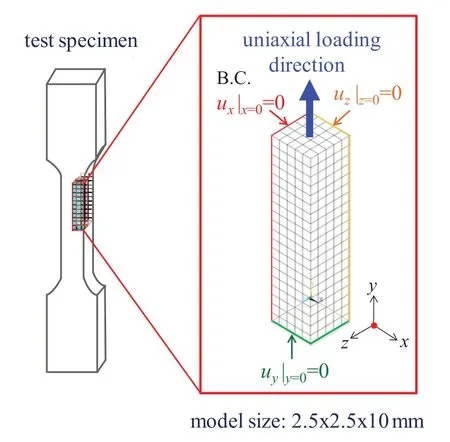
Figure 3:Finite element model of the solder rod under uniaxial cyclic loading

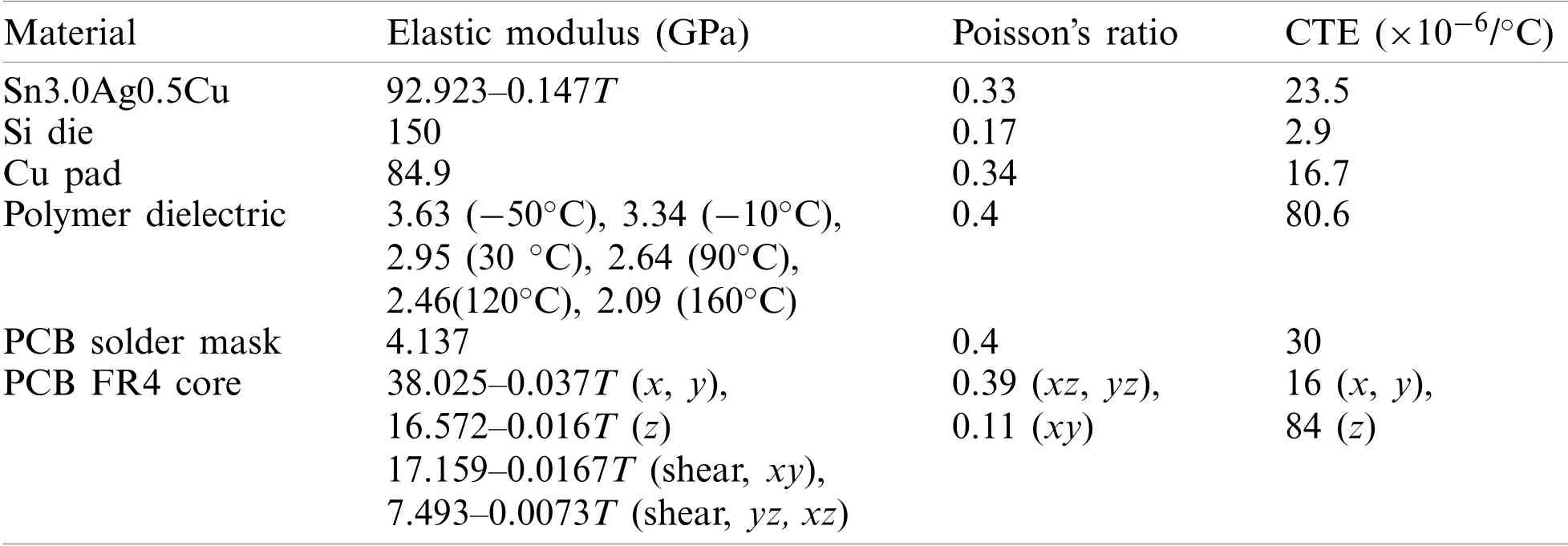
Table 2:The thermomechanical properties of the electronic assembly (T in K)

The FE model was first applied to consider the solder response under cyclic straining with a constant rate of 2 × 10−51/s and at temperatures of 75 and 125◦C.The strain waveform was triangular with a symmetric range of ±0.2%.In the numerical simulation,each half-cycle of the triangular wave was considered as one load step in the solution process,and the solution step size was controlled by the ANSYS built-in automatic time-stepping strategy.For each load step,the minimum number of sub-steps was set as 48 per load step,and the eventual number of sub-steps was about 50 per load step.Shown in Fig.4 are the hysteresis loops obtained from the numerical model and the corresponding experimental results.It can be seen from Fig.4 that the numerical results exhibit cyclic softening response,which agree well to the experimental observations.The effect of step size on the numerical solution was considered by solving the problem with either 5 or 30 uniform sub-steps per half-cycle and comparing the results to the automatic time-stepping solution,which is denoted as the baseline.The comparisons of the various numerical solutions for the first 10 strain cycles are shown in Fig.5.It can be seen from Fig.5 that the 30-sub-step procedure gives stress solutions practically the same as the baseline,while the 5-sub-step procedure under-estimates the peak stress slightly by about 3% for both the 75 and 125◦C cases.

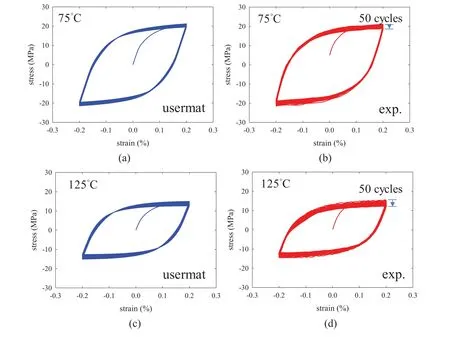
Figure 4:Solder responses under cyclic straining with strain range of ±0.2%,(a)simulation result,at 75◦C,(b)experimental result,at 75◦C,(c)simulation result,at 125◦C,(d)experimental result,at 125◦C

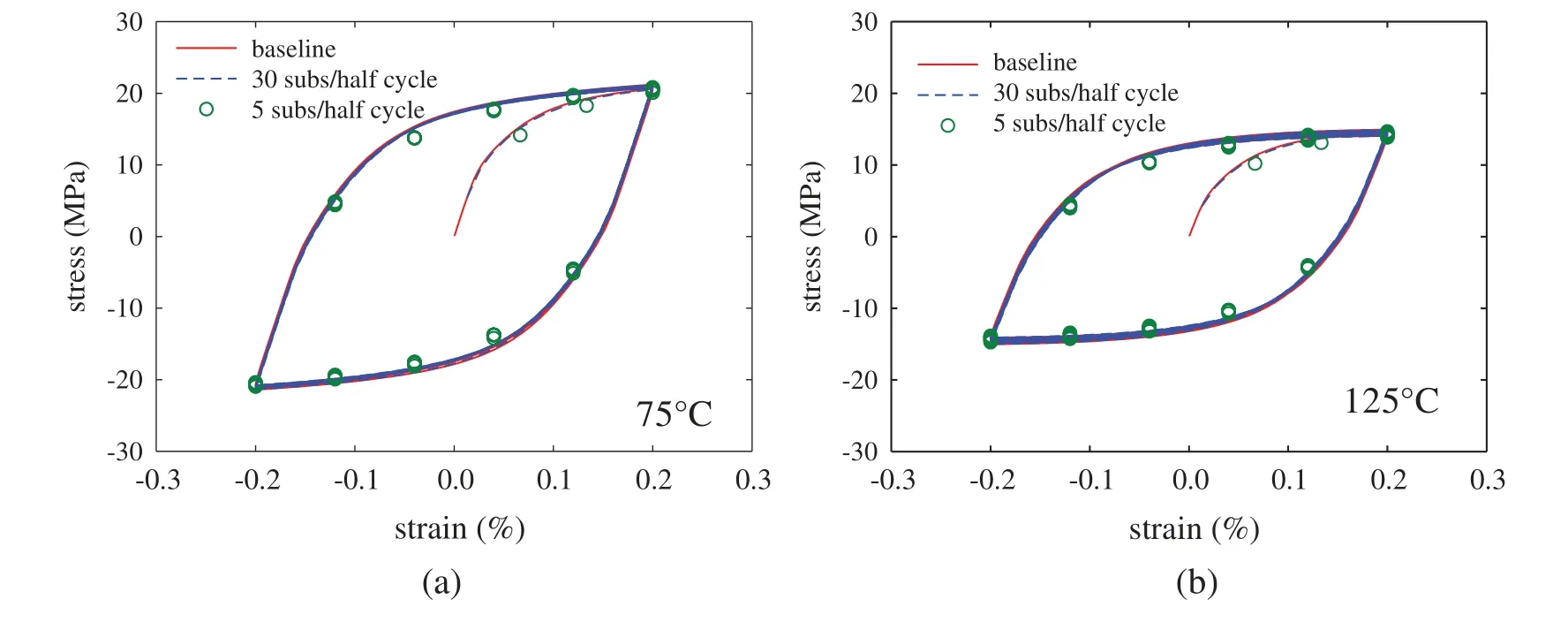
Figure 5:Effect of solution step size on simulation results for cyclic straining under strain range of ±0.2%,(a)at 75◦C,(b)at 125◦C

The cyclic response of the solder rod under a triangular strain wave of range 0%–0.25%was also considered by using the FE model shown in Fig.6.The cyclic loading was applied at a constant strain rate of 2 × 10−51/s and at temperatures of 25 or 125◦C.The simulation was first conducted with automatic time-stepping strategy with the minimum number of substeps set as 38 for each load step (half cycle).The eventual number of sub-steps was about 40 per half-cycle.As shown in Fig.6,the hysteresis loops obtained from the numerical simulation compare well with the experimental data.It can also be seen from Fig.6 that the cyclic softening behavior also exists when the mean strain value of the fatigue cycle is not zero.To evaluate the influence of solution step size for the case of 0%–0.25% strain range,the numerical solutions of the procedures using either 3 or 20 uniform sub-steps per half-cycle are compared to the baseline,automatic time-stepping solution.The comparisons of the various numerical solutions for the first 10 strain cycles are shown in Fig.7.It can be seen from Fig.7 that the 20-sub-step procedure gives stress solutions practically the same as the baseline,while the 3-sub-step procedure underestimates the peak stress by about 6.5% for the 25◦C case and 5.5% for the 125◦C case.From the step-size comparisons shown in Figs.5 and 7,it can be concluded that the numerical stress solution is affected by the sub-step,and that a larger number of uniform sub-steps or automatic time-stepping allows a converged stress solution in the strain-controlled cyclic loading conditions.

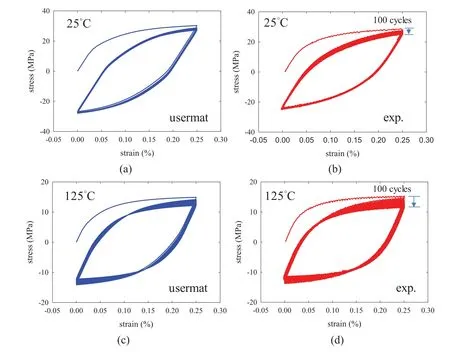
Figure 6:Solder responses under cyclic straining with strain range of 0%–0.25%,(a)simulation result,at 25◦C,(b)experimental result,at 25◦C,(c)simulation result,at 125◦C,(d)experimental result,at 125◦C

Figure 7:Effect of solution step size on simulation results for cyclic straining under strain range of 0%–0.25%,(a)at 25◦C,(b)at 125◦C

The ratcheting response of the Sn3.0Ag0.5Cu rod under cyclic stress loading at constant temperature of 75◦C was also considered by using the model as shown in Fig.8.The cyclic stress waveform is triangular in the range of 7.28 and 21.8 MPa,and has a constant rate of 0.91 MPa/s.The numerical solutions were obtained with either the automatic time-stepping strategy or uniform steps.In the case of automatic time-stepping,the minimum number of sub-steps for each load step (half-cycle)was set as 48,and the eventual number of sub-steps was about 49 steps per load step.

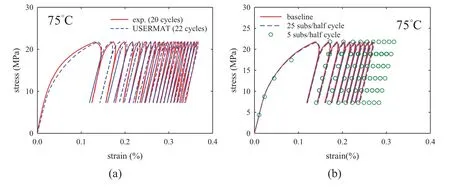
Figure 8:Ratcheting responses under cyclic stressing test at 75◦C,(a)simulation result compared to experimental data (b)effect of solution step size on simulation results

In the cases of uniform steps,the sub-step numbers of 5 and 25 were considered.Shown in Fig.8 are the results of the ratcheting simulations.The comparison of the automatic timestepping solution to the experimental results is shown in Fig.8a,from which it can be seen that the numerical results correlate well to the experimental data.The effect of time-stepping strategy on the numerical ratcheting solution is shown in Fig.8b.It can be seen from Fig.8b that the 25-sub-step procedure gives stress solutions practically the same as the automatic time-stepping solution,which is denoted as the baseline.On the other hand,the 5-sub-step procedure clearly over-estimates the ratcheting strain,especially for the first few cycles.The poor numerical result for the 5-sub-step case can be attributed to the low tangent modulus of the solder,which would lead to a higher simulation error when large stress step is assigned in the incremental strainbased iterative scheme.A similar observation was also made in [23].From the comparisons of the numerical results shown in Figs.5,7 and 8,it can be seen that the incremental step size has a stronger influence on the numerical solutions of the stress-controlled problems than that of the strain-controlled problems.

4.2 BGA Solder Joints under Temperature Cycling

The viscoplastic responses of the BGA Sn3.0Ag0.5Cu solder joints in the assembly of a wafer-level package (WLP)on PCB under a standard −40◦C/125◦C temperature cyclic reliability test was considered by using the FE simulation.The WLP considered has an overall size of 4.5 mm × 4.5 mm,with 0.4 mm-pitch,10 × 10 array of solder joints,and the test PCB has an overall size of 7.2 mm × 7.2 mm.Shown in Fig.9 is the cross-sectional schematic of the boardlevel assembly.In the assembly,the barrel-shaped solder joints are formed between Cu pads on both the package and the PCB sides.The solder-Cu interconnection is in a bump-on-trace (BOT)configuration on the package side,and is in a non-solder-mask defined (NSMD)configuration on the PCB side.The Si chip thickness,the solder joint height and the PCB thickness are 0.28,0.16 and 1 mm,respectively.By taking advantage of the geometrical symmetry of the assembly,a quarter FE model with symmetric boundary conditions as shown in Fig.10 was developed for the temperature-cycling simulation.The model was constructed by using the submodeling approach in which a “unit-cell” of the assembly at the critical solder joint location is meshed with fine elements to ensure accuracy,the rest of the model is populated with relatively coarse elements to reduce solution time,and displacement couplings are reinforced at the interfaces of the densely and coarsely meshed regions.The model as shown in Fig.10 contains 20781 quadratic (solid 186)elements,among which 7608 elements are in the “unit cell”.In this model,only the behavior of the Sn3.0Ag0.5Cu solder joint is considered as inelastic,while the other materials are assumed as linear elastic with temperature dependent thermomechanical constants given in Tab.2.For evaluating the mesh convergence and the computation efficiency,uniform cooling of the assembly as shown in Fig.9 from 125 to −40◦C in 600 s were considered by using the quarter model with various local mesh density as shown in Fig.11.The numerical results obtained by using a personal computer with Intel Core i7-8700 processor under 6-core shared-memory parallel mode are shown in Fig.12 and Tab.3.It can be seen from Tab.3 that the difference in maximum stress values is less than 4%,while the solution time increases significantly for the two finest meshes.As such,the baseline FE mesh with 1728 solder elements in Figs.10 and 11 were used for the temperature cycling simulation.

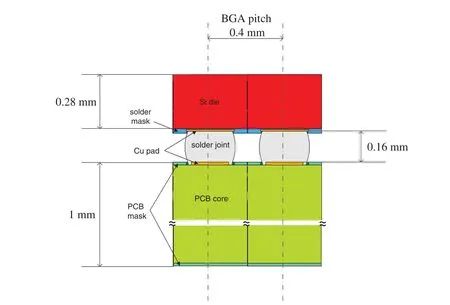
Figure 9:The cross-section schematic of a WLP assembled on PCB

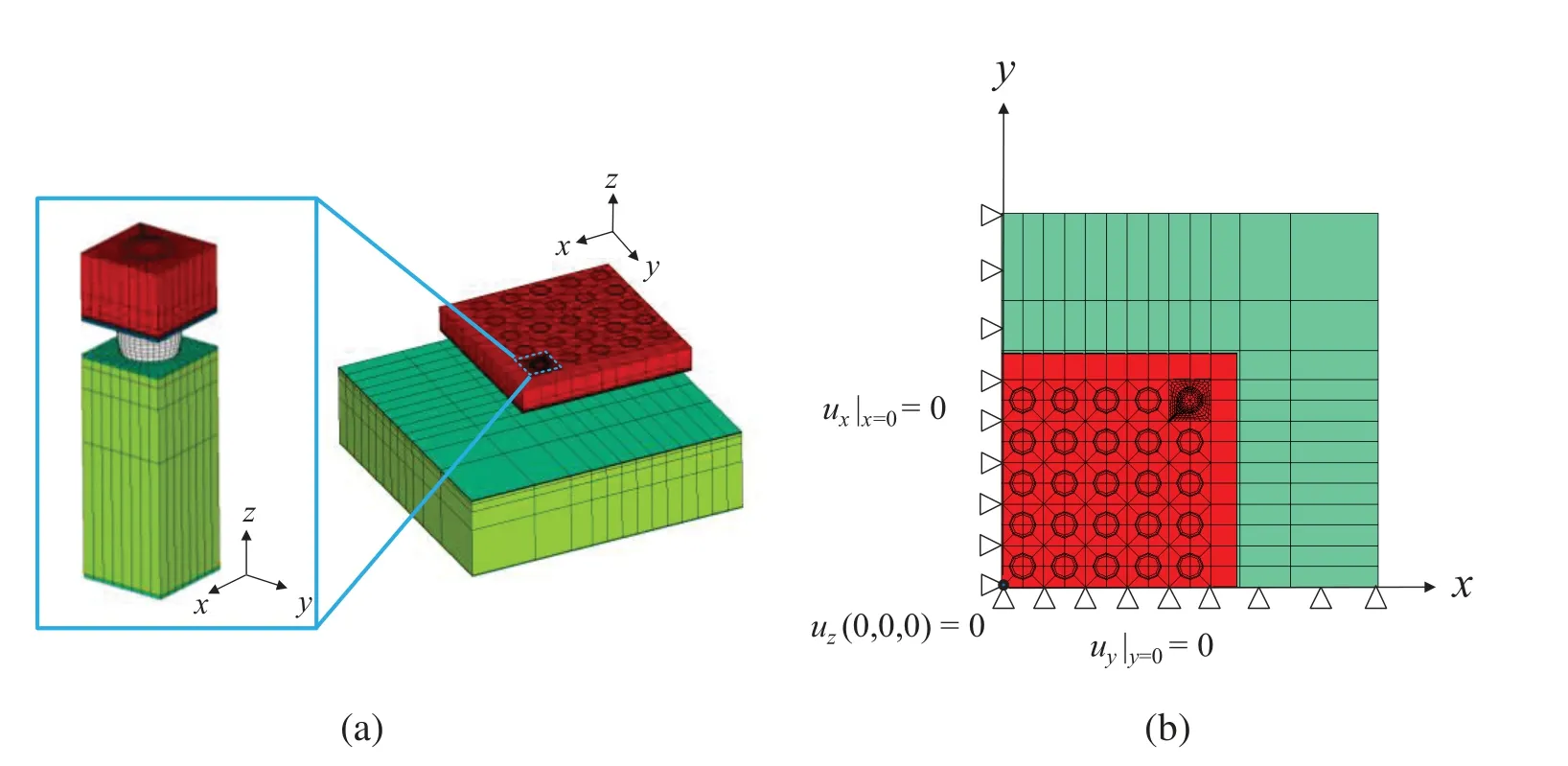
Figure 10:Finite element model of the WLP assembled on PCB (a)the submodeling FE mesh,(b)boundary conditions

Shown in Fig.13 is the −40◦C/125◦C temperature cycling profile considered in this simulation.Each temperature cycle consists of two 600-s linear temperature ramping (from −40 to 125◦C,and from 125 to −40◦C)stages and two 600-s temperature dwelling (at −40 and 125◦C)stages.It was shown from experimental investigation [35] that the process-induced residual stress in electronic package is zero near the glass transition temperature of the laminate PCB,which is also around 125◦C.It is therefore assumed that the assembly is stress-free at 125◦C and the thermal stress is the highest at the lower bound temperature during temperature cycling.In the simulation,the temperature cycling load was applied in a repeating sequence of cooling from 125 to −40◦C,dwelling at −40◦C,heating from −40 to 125◦C and dwelling at 125◦C.For the solution control,each of the temperature ramping or dwelling stages was assigned as one load step.Within each load step,ANSYS automatic time stepping strategy with initial sub-step size for each load step was set as 5 s (1/120 of the load step).The averaged solution sub-steps were 33 for the ramping stages,and was 16 for the dwelling stages.

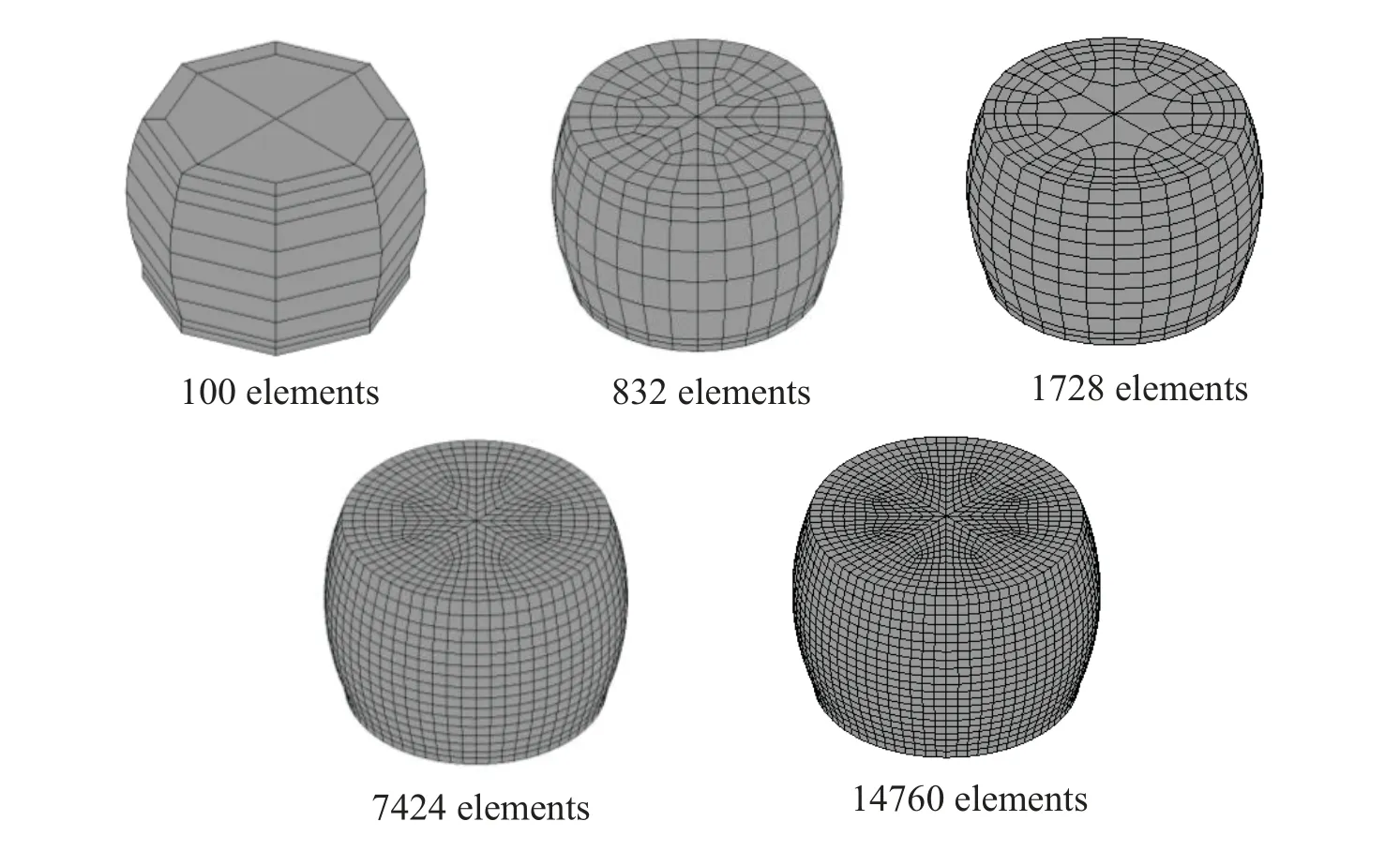
Figure 11:Various meshes of the critical solder joint

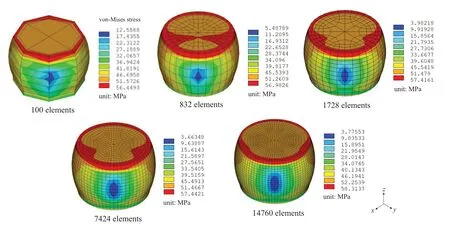
Figure 12:The von-Mises stress contour of the critical solder joint

Table 3:Effect of mesh density on stress and computation time

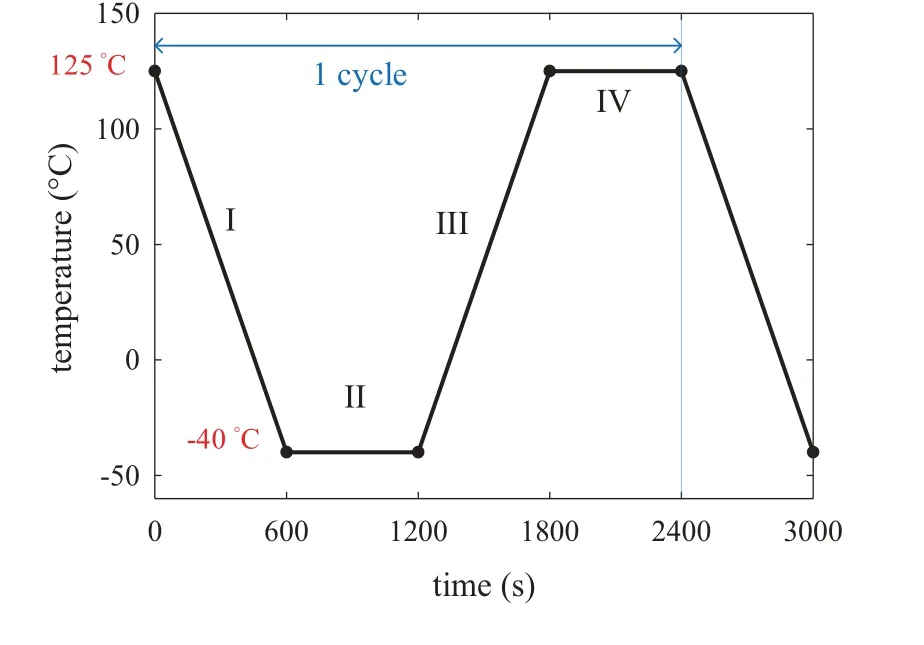
Figure 13:The −40◦C/125◦C temperature cycling profile

The von-Mises stress distribution in the critical solder joint at the end of the cooling stage of the 11th cycle is shown in Fig.14.Because the thermal strain is the highest at −40◦C,it is expected that the thermal stress is also the most significant at this state.It can be seen from Fig.14 that high stress concentration occurs around the copper pad.Furthermore,the magnitude of solder stress around the package Cu pad is higher on the side away from the center of package,which is consistent with the location of crack formation in experiments [36].The viscoplastic equivalent strain accumulation in the critical solder joint at the end of the 20th cycle is shown in Fig.15,from which it can be seen that the equivalent viscoplastic strain concentration zone is consistent with the von-Mises stress distribution as shown Fig.14.To further examine the solder joint response under the temperature cycling condition,the shear stress-viscoplastic shear strain relationship near the outer corner of the critical solder joint on the package side was monitored and is shown in Fig.16.It can be seen from Fig.16 that the shear stress reaches peak value at the end of cooling stage,and that the viscoplastic shear strain accumulates at a relatively constant rate as the number of temperature cycle increases.

In addition to the stress and strain solutions,the viscoplastic strain energy density is another parameter considered extensively in the semi-empirical approaches for predicting temperature cycling reliability of solder joints [36,37].The viscoplastic strain energy density is given by

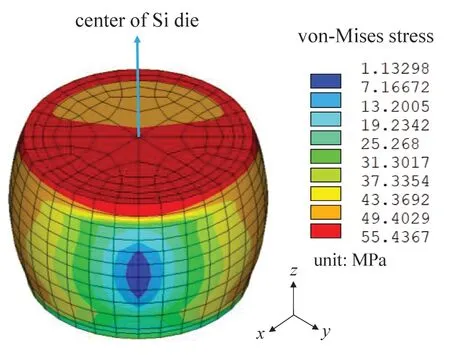
Figure 14:von-Mises stress distribution in the critical solder joint

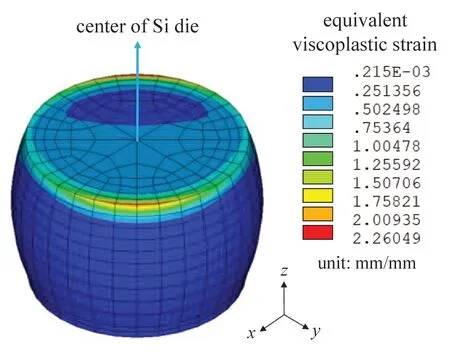
Figure 15:Equivalent viscoplastic strain in the critical solder joint

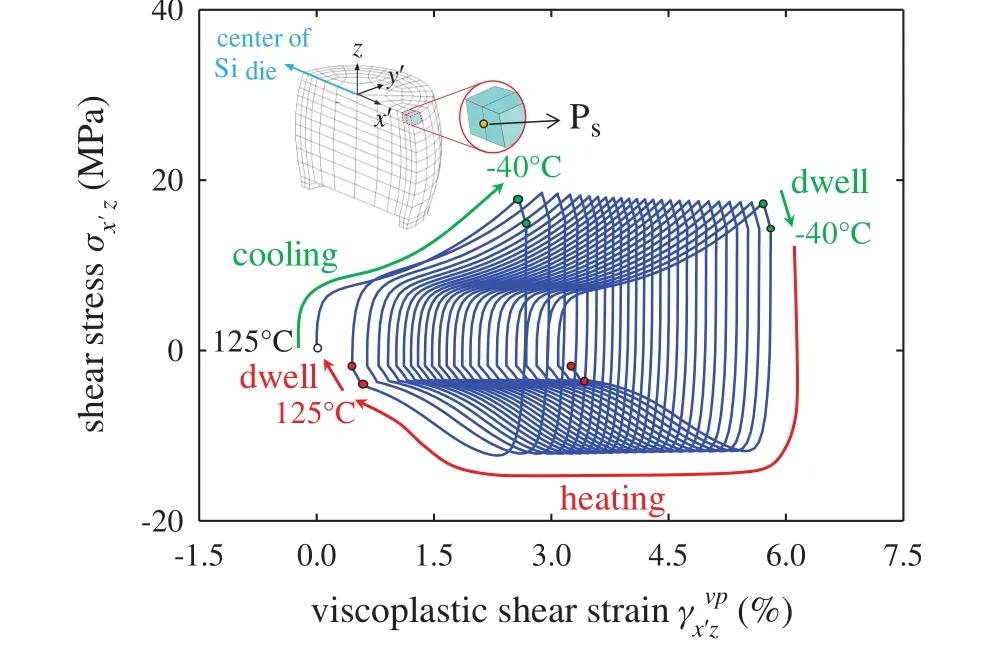
Figure 16:Shear stress-viscoplastic shear strain relationship at the point Ps

The viscoplastic strain energy density is evaluated at each element in an incremental fashion.For each solution sub-step,the viscoplastic strain energy density increment is calculated in the USERMAT subroutine by using trapezoidal integration.The volume-averaged viscoplastic strain energy density is defined as

whereVis the volume of the element.By following Darveaux’s approach [37],the volumeaveraged viscoplastic strain energy density (Wavg)in the 25-μm disk region next to the packageside Cu pad interface at the critical solder joint was calculated and is shown in Fig.17.It can be seen from Fig.17a that the accumulation of the volume-averaged viscoplastic strain energy density increases at a relatively constant rate over the temperature cycles.In addition,the increases inWavgoccur mainly during the temperature ramping stages of the cycles,as shown in Fig.17b.The volume-averaged viscoplastic strain energy density increment accumulated over one temperature cycle (ΔWavg),which has a relatively linear relationship to the fatigue crack growth rate in the semi-empirical temperature-cycling solder joint reliability models [37],was also calculated and is shown in Fig.18.It can be seen from Fig.18 that the value ofΔWavgis relatively unchanged after the second cycle.Consequently,ΔWavgcan be served as a quantitative indicator in the numerical simulation procedure described in this paper to establish the solder-joint reliability model under temperature-cycling condition.For enabling quantitative reliability prediction,it would require additional FE simulations and correlation to experimental data in a similar fashion to [37] for establishing the solder joint fatigue crack growth model.

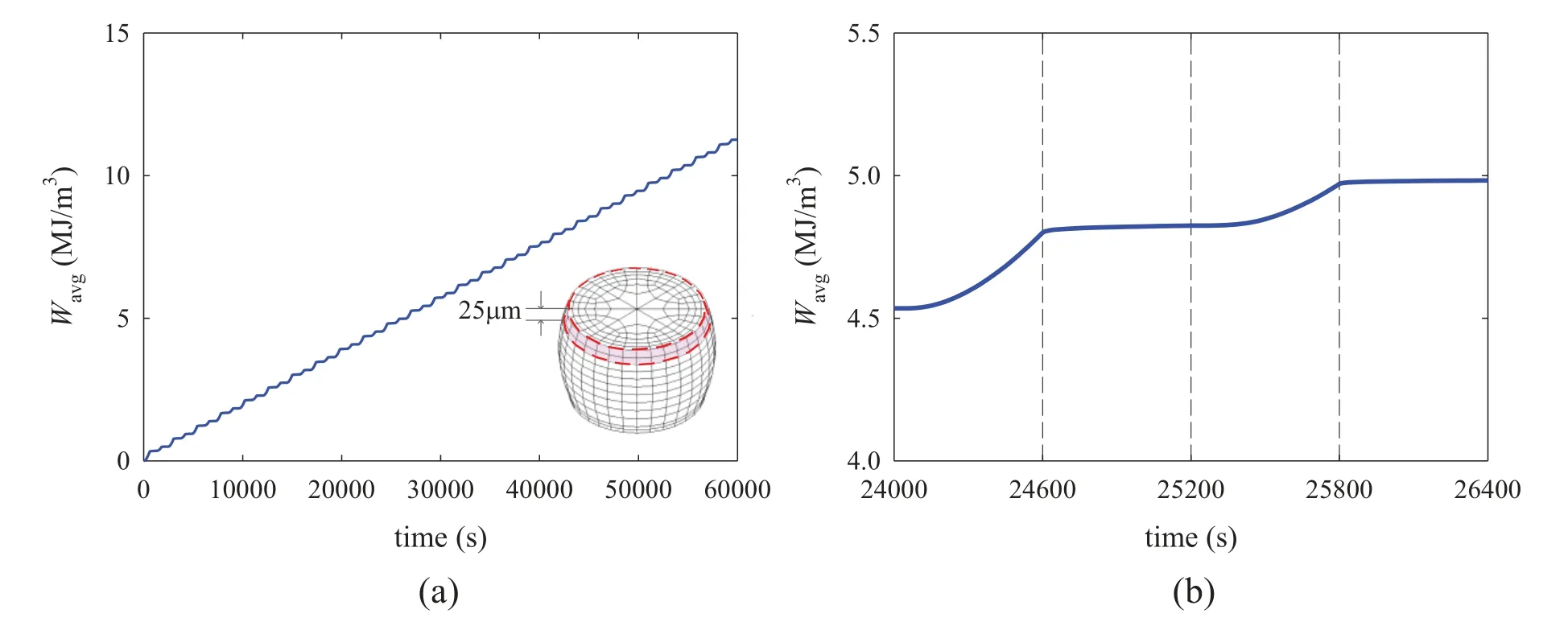
Figure 17:The volume-averaged viscoplastic strain energy density near the package-solder interface (a)the evolution over time,(b)zoom-in at the 11th cycle

Figure 18:The volume-averaged viscoplastic strain energy density increment per cycle

5 Conclusions

A fully implicit integration procedure was developed for a unified viscoplastic constitutive model and implemented as a user-defined material subroutine (USERMAT)in the commercial FE software ANSYS.In the numerical implementation,a Chaboche framework based viscoplastic model that considers the cyclic softening behavior of Sn3.0Ag0.5Cu solder was first discretized as a set of nonlinear system of equations for 26 unknowns.Additional simplification was applied to reduce the nonlinear system to solving four equations for four essential variables.The implicit integration scheme first solves the four essential variables by using a three-level,Newton-Raphson and Pegasus method based iterative procedure,and updates the remaining stresses and state variables accordingly.A consistent tangent modulus for the constitutive equation was also derived and implemented in the USERMAT subroutine.Validation of the USERMAT was accomplished by simulating the solder rod responses under either strain-or stress-controlled cycling and compared to experimental measurements.It was shown that the numerical model is capable of predicting the softening response under cyclic straining and the ratcheting response under cyclic stressing.A FE model of WLP connected to PCB through BGA solder joints was also developed to simulate the solder joint response under board-level temperature cyclic condition.From the simulation,the viscoplastic strain energy density accumulation over one temperature cycle was identified as a feasible parameter for evaluating the thermomechanical reliability of the of solder joints in electronic assembly.

Funding Statement:This study was supported by the Ministry of Science and Technology,ROC,under the Grants MOST 107-2221-E-006-138 and MOST 109-2221-E-006-008 MY2.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.