Mathematica在分离变量法中的应用及极限情况下的讨论*
汪梦雅 曹 蓉 夏杰桢 吴 琪
(西藏大学理学院 西藏 拉萨 850000)
静电场问题是电磁学理论之后又一个重要的理论知识,是电动力学里的一个核心问题[1,2].其基本问题就是求解关于静电势的泊松方程的边值问题,解法主要有分离变量法、格林函数法、镜像法和电多极矩法等,其中最常用的两种解法是分离变量法和镜像法[3].
由于电动力学的数学要求远比普通理工科专业高,所以为了能将学生从复杂的微分方程、偏微分方程的求解过程中解放出来,引入了Mathematica[4].Mathematica是美国WolframResearch公司开发的数学软件,是现在使用最广的软件之一.该软件除了很好地结合了数值和符号计算之外,还具有强大的绘图功能,操作简单,界面友好,代码形式接近于自然语言,广泛用于数学、物理、生物等领域[5~7].
本文利用Mathematica求解静电场中分离变量法的问题出发,并讨论在这种问题下的一些极限情况来探讨Mathematica在静电场中的应用.通过Mathematica的使用消除学生对复杂公式的畏惧,使学生可以摆脱繁琐的数学计算,并且通过Mathematica的绘图使学生对物理图像有个较为直观准确的认识,激发学生的兴趣,促进课程的学习.
1 静电场的标势及其微分方程
1.1 静电场的标势
众所周知,相距为dl的两点的电势差为[8]
dφ=-E·dl
(1)
然后由于
(2)
因此,电场强度E等于电势φ的负梯度
(3)
1.2 静电场的微分方程和边值关系
研究一个电荷对与它邻近的电场是怎样作用的,一点上的电场和它邻近的电场又是怎么联系的,即要找出电荷和电场相互作用规律的微分形式,而在导体表面或其他边界上场和电荷的相互关系则由边界条件反映出来.这种问题称为边值问题,即求微分方程满足边界条件的解.
在均匀同向的介质中,D=εE,再把式(3)代入
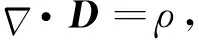
(4)
其中ρ是自由电荷密度.式(4)是静电势满足的基本微分方程,也就是泊松方程,给出边界条件就可以确定电势φ的解.
在两介质界面上,静电势所满足的边值关系分别为
φ1=φ2
(5)
(6)
以上是边值关系的一般形式,但是在静电问题中,常常有一些导体存在,由于导体的特殊性质,在导体表面上的边值关系有它的特点.设导体表面所带自由电荷面密度为σ,它外面的介质电容率为ε,则由式(5)、(6)和导体静电条件得到导体表面的边界条件
φ=常量
(7)
(8)
静电学的基本问题就是求出在每个均匀区域内满足泊松方程,在所有分界面上满足边值关系和在所研究的整个区域边界上满足边界条件的电势的解.
2 分离变量法求解的方程和通解
在许多实际问题中,静电场是由带电导体决定的[9].比如,电容器内部的电场是由作为电极的两个导体板上所带电荷决定的,电子光学系统的静电透镜内部,电场是由分布于电极上的自由电荷决定的.这些问题都有一个共同的特点,就是自由电荷只出现在一些导体的表面上,而在空间中没有其他自由电荷分布.这时,当选择这些导体表面作为区域V的边界,则在V内部自由电荷密度ρ=0.此时泊松方程可以化为较为简单的拉普拉斯方程(拉式方程),即
(9)
因此,这一类问题的解法就是求满足边界条件的拉普拉斯方程的解.此拉普拉斯方程的通解可以用分离变量法求出,在求解前我们要先选择合适的坐标系,常用的坐标系有球坐标系和柱坐标系,在这里我们写出用球坐标系得出的通解形式,球坐标用(r,θ,φ)表示,其中r为点到原点的距离,θ为极角,φ为方位角,拉式方程在球坐标中的通解为
(10)
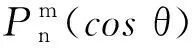
(11)
其中Pn(cosθ)为勒让德函数,an和bn是任意常数,由边界条件或者说由边值关系确定.
在每一个没有电荷分布的区域内,φ满足拉普拉斯方程,其通解已由式(10)和式(11)给出,剩下的问题就是由边界条件确定这些通解中所含的任意常数,得到满足边界条件的特解.
3 分离变量法的实际应用
【例题】一半径为a,介电常数为ε的介质球放置在均匀电场E0中,如图1所示,求介质球内、外的电位及电场.
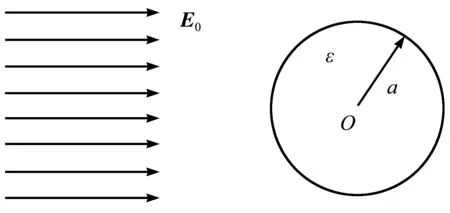
图1 题图
分析:介质球在外电场中极化,在它表面上产生束缚电荷.这些束缚电荷激发的电场叠加在原外电场E0上,得总电场E.束缚电荷分布和总电场E互相制约,边界条件正确的反映这种制约关系.
球的半径为a,球外为真空,这问题具有轴对称性,对称轴为通过球心沿外电场E0方向的轴线,取此轴为极轴.介质球的存在使空间分为两均匀区域,球外区域和球内区域,两区域内部没有自由电荷,因此电势φ都满足拉普拉斯方程,以φ1代表球外区域的电势,φ2代表球内的电势,由式(11)得出的两区域的通解为
(12)
(13)
式中an,bn,cn,dn是待定常数.
边界条件有:
(1)无穷远处,E→E0,均匀电场中空间任一点P的电势φ(P)=φ0-E0·x,由于均匀电场可以看作由无穷大平行板电容器产生,其电荷分布不在有限区域内,因此不能选φ(∞)=0.若选φ0=0,则有φ(P)=-E0·x,可得
φ1→-E0rcosθ=-E0rP1(cosθ)
(14)
所以有
a1=-E0an=0(n≠1)
(15)
(2)r=0处,φ2应为有限值,因此
dn=0
(16)
(3)在介质球面上(r=a)
(17)
把式(12)和(13)代入得
(18)
比较P1的系数得
(19)
由式(19)解出
(20)
比较式(18)其他Pn项的系数可解出
bn=cn=0n≠1
(21)
所有常数已经定出,因此本问题的解为
(22)
(23)
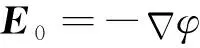
为了简化运算,用Mathematica来求解本题,并画出介质球附近的电场线和等位面图.所需代码如下所示:
Clear["Global′*"]
v1=Sum[(An*R^n+Bn/R^(n+1))*Pn,{n,0,m})]
v2=Sum[(Cn*R^n+Dn/R^(n+1))*Pn,{n,0,m})]
v1=Sum[(An*R^n+Bn/R^(n+1))*Pn,{n,0,1})]/.{P0→1,P1→Cos[θ]}
v2=Sum[(Cn*R^n+Dn/R^(n+1))*Pn,{n,0,1})]/.{P0→1,P1→Cos[θ]}
(v1/.{B0→0,B0→0})==-E0*R*Cos[θ]
A0=0;A1=-E0;
D0=0;D1=0;
(v1/.R→a)==(v2/.R→a)
(ε0D[v1,R]/.R→a)==(εD[v2,R]/.R→a)
B0=0;
C0=0;
sol=Solve[{eq1,eq3},{B1,C1}]
v11=v1/.sol//First
v22=v2/.sol//First
E1=Grad[-v11,{R,θ,φ},"Spherical"]//
Simplify
E2=Grad[-v22,{R,θ,φ},"Spherical"]//
Simplify
E2=Grad[-v22,{x,y,z},"Cartesian"]
≪VectorFieldPlots′;
GradientFieldPlot[-v3,{z,-2,2},{x,-2,2},PlotPoints→20]
Plot3D[v3,{z,-2,2},{x,-2,2},PlotPoints→30,LabelStyle→(FontSize→20),BoxRatios→{1,1,1}]
Mathematica绘制出的电场线图和等电位图如图2所示.

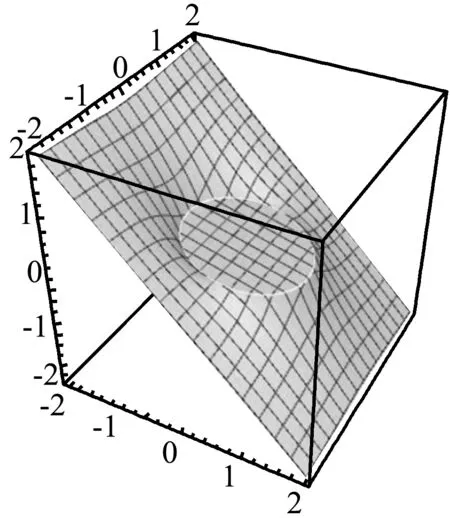
(a)电场线图

接下来对这题做一些极限情况下的讨论:
(1)第一种极限情况:当ε=ε0时,介质球与环境的介电常数一样,其对外场的响应消失,把其代入式(22)、(23),此时φ1=φ2=-E0rcosθ空间的电场就是均匀电场.用Mathematica来分析此时的电场,绘制电场线图的主要代码如下所示,绘制的电场线图如图3所示.
Clear["Global′*"]
v11=-E0RCos[θ]
v22=-E0RCos[θ]
Grad[-v11,{R,θ,φ},"Spherical"]//Simplify
E2=Grad[-v22,{R,θ,φ},"Spherical"]//
Simplify
v22=-E0x;
E2=Grad[-v22,{x,y,z},"Cartesian"]
≪VectorFieldPlots′;
GradientFieldPlot[-v3,{z,-2,2},{x,-2,2},PlotPoints→20]

图3 极限情况1下介质球附近的电场线图
结合φ1=φ2=-E0rcosθ和图3进一步验证了此种情况下的电场为匀强电场.
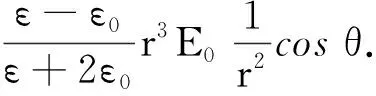
(24)
介质球的总电偶极矩为
(25)
式(22)φ1中的第二项正是这个电偶极矩所产生的电势
(26)
由于此时的外电场相当于偶极子产生的电场,所以用Mathematica来绘制偶极子的电场来近似这种情况下的电场,Mathematica的代码如下所示:
Clear["Global′*"];
V=q/(4*Pi*Subscript[ε,0])*(1/r1-1/r2)
cond={r1→R-l/2*Cos[θ],r2→R+l/2*
Cos[θ]}
V=V/.cond//SimplifySeries[V,{l,0,6}]//
Normal
Solve[V1==c,R]
Ee=Grad[-V1,{R,θ,ω},"Spherical"]
D[R[θ],θ]/R[θ]==Ee[[1]]/Ee[[2]]
DSolve[%,R[θ],θ]
g2=PolarPlot[Evaluate[Table
Identity];
Show[{g1,g2},DisplayFunction→$Display
Function,Epilog→{PointSize[0.03],Hue[2],
Point[{0,-2.5}],PointSize[0.03],Hue[.3],
Point[{0,2.5}]}]
V1[θ_,R_]:=cos[θ]/R2
RevolutionPlot3D[V1[θ,R],{R,0.01,3},{θ,0,2π},PlotRange→{-3,3},PlotPlints→30,
BoxRatios→{1,1,1}]
Mathematica绘制出的第二种极限情况下也就是电偶极子的电场线图和等位面图如图4所示.
从图4(a)中可以看出电偶极子的整个电场和电势是一个数值分布对称的区域,整个图形是以电偶极子的轴线对称的.再看图4(b),发现在正电荷附近电偶极子的电势比较高;而在负电荷附近,电偶极子的电势比较低,且在电偶极子的中垂线上电势为零.
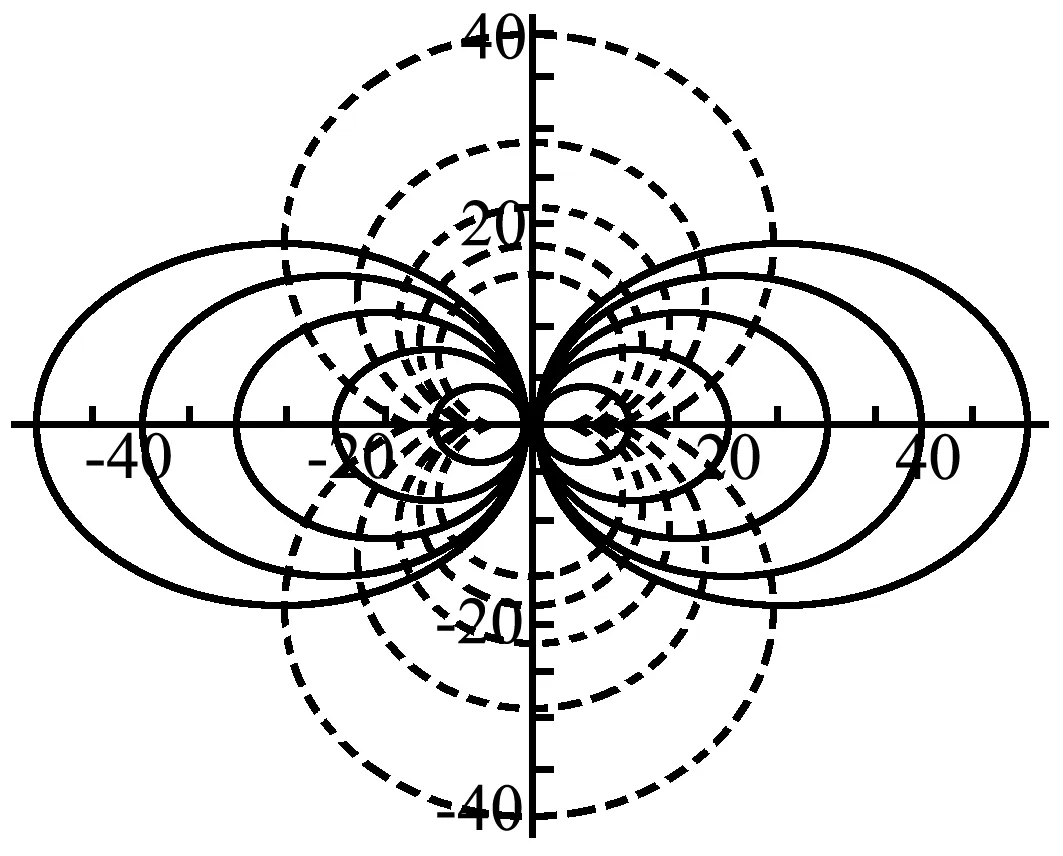
(a)电场线图
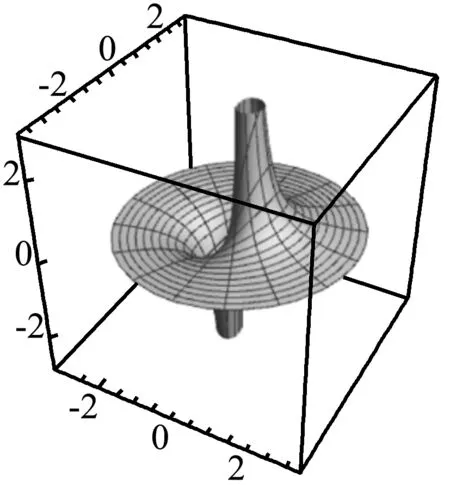
(b)等位面图
(3)当ε→-∞时,介质球内的场为E内→0,其效果相当于一个导体球.而此时,p=4πε0a3E0,问题就变成了求解导体球附近的电场,所以,我们可以用导体球的情况来近似这种情况下的电场分布,求导体球附近的电场的Mathematica代码如下所示:
Clear["Global′*"]
v=Sum[(An*R^n+Bn/R^(n+1))*Pn,{n,0,∞}]
v=Sum[(An*R^n+Bn/R^(n+1))*Pn,{n,0,1}]/.{P0→1,P1→Cos[θ]}
(v/.{B0→0,B1→0})==-E0*R*Cos[θ]
cond1={A1→-E0,A0→0};
(v/.cond1/.R→a)==0
cond2={B1→a^3E0,B0→0};
v=v/.cond1/.cond2
GradientFieldPlot[-v1[z,x],{z,-2.,2.},{x,-2.2.},PlotPoints→20,Epilog→{Hue.
[.6],Disk[{0,0},1]}]
Mathematica绘制出的第三种极限情况下也就是导体球附近的电场线如图5所示.

图5 导体球附近的电场线图
从图中我们发现,导体球外的电场分布规律和介质球外的电场分布规律是一样的,但是在这种情况下,导体球内部是没有电场存在的.因为当导体置于电场中时,导体内的电荷会重新分布,形成电场来抵消外电场,最终就会导致导体内的总电场为零.
4 结论
本文基于Mathematica讨论了分离变量法在静电场的应用,通过用分离变量法求解介质球附近的电场以及3种极限情况下电场分布的实例分析展示了Mathematica具有的强大的数值计算、符号计算和图形绘制的功能,研究探讨了如何通过Mathematica软件辅助静电场的学习.学生通过学习Mathematica软件,能够很好地锻炼动手能力和自主学习能力,他们在学习过程中可以将专业课的复杂数学问题交给Mathematica来进行,而自己只需掌握基本的数学原理,了解相关知识,配合Mathematica图形显示,就能达到更充分更深层次理解内容本质的目的,尤其是西藏地区来自农牧区的学生,数理基础很差,Mathematica的引入解决了这些学生由于薄弱的数学基础和抽象的专业概念所引起的在专业课学习上的困难,对这些学生具有重大意义.

