Stability Reliability of the Lateral Vibration of Footbridges Based on the IEVIE-SA Method
Buyu Jia,Siyi Mao,Quansheng Yan and Xiaolin Yu
School of Civil Engineering and Transportation,South China University of Technology,Guangzhou,510640,China
ABSTRACT Research on the lateral vibrational stability of footbridges has attracted increasing attention in recent years.However,this stability contains a series of complex mechanisms,such as nonlinear vibration,random excitation,and random stability.The Lyapunov method is regarded as an effective tool for analyzing random vibrational stability;however,it is a qualitative method and can only provide a binary judgment for stability.This study proposes a new method,IEVIE–SA,which combines the energy method based on the comparison between the input energy and the variation of intrinsic energy(IEVIE)and the stochastic averaging(SA)method.The improved Nakamura model was used to describe the lateral nonlinear stochastic vibration of a footbridge,whereby the IEVIE method was used to establish the criteria for judging the lateral vibrational stability.Additionally,the SA method was used to deduce the corresponding backward Kolmogorov equation.Subsequently,the backward Kolmogorov equation was combined with the stability criterion established by the IEVIE method to analyze the first passage stability.The proposed method is a semi-analytical,quantitative method that only requires a small calculation.By applying the proposed method to the Millennium Bridge,method effectiveness was verified by comparing it with the Monte Carlo and traditional Lyapunov methods.
KEYWORDS Footbridge; vibration; stability; energy; stochastic; reliability
1 Introduction
Research on footbridge vibrations consists of two primary directions:vertical and lateral.During vertical vibration,it is generally believed that pedestrian excitation is rarely affected by bridge vibration,and few phenomena of vertical vibration instability have been observed.Thus,the vertical vibration of a footbridge is often regarded as a linear vibration system [1].Compared to vertical vibration,the lateral vibration of a footbridge is much more complex.During lateral vibration,it has been shown that pedestrian lateral load depends on the vibration of a bridge,resulting in a nonlinear system [2].Additionally,the occurrence of lateral vibration instability of a footbridge has been frequently observed.For example,sudden large lateral vibrations have been observed on the Millennium Bridge [3],the Paris Solferino Bridge [4],and the Singapore Changi Airport Bridge [5,6].In addition to the characteristics of nonlinear vibration,lateral vibration of a footbridge is a stochastic process,and pedestrian excitation is a narrow-band stochastic process rather than a deterministic periodic process [7,8] because of intra-subject variability.
Thus,the object of this study was essentially a complex system with nonlinear,stochastic vibrational stability.Until now,representative models used to explain the lateral vibration instability of footbridges include the Dallard et al.[3],Nakamura et al.[9],Piccardo et al.[10],Ingólfsson et al.[11],and inverted pendulum models [12].The Dallard and Nakamura models belong to the velocity-dependent,nonlinear model class.In this kind of model,the velocity-dependent part can be regarded as virtual negative damping to the bridge.When the virtual negative damping exceeds the structural damping,the vibration will lose stability.The Piccardo model involves parametric resonance,in which the dynamic equation can be transformed to the classical Matthew parametric equation with stability condition.The Ingólfsson model primarily focuses on the self-excited loads consisting of an acceleration-proportional component and a velocity-proportional component.The velocity-proportional component can be regarded as virtual damping.Like the velocity-dependent model,when the total damping is negative,the stability will lose.Unlike the general models,the Macdonald model (also known as the inverted pendulum model)requires that pedestrians rely on adjusting step position rather than step frequency to maintain their own comfort and balance.This includes an intricate implication:synchronization is not a prerequisite for large lateral vibration.Regardless,whether the walking frequency is close to the bridge frequency or not,pedestrians always yield self-excited loads.The stability condition can be obtained by considering the component in phase with velocity as a virtual damping.The Ingólfsson and Macdonald models have been used for random vibration analysis.However,the random analysis method that they use is a numerical simulation,i.e.,Monte Carlo (MC)method,which needs massive calculations.Ingólfsson et al.[13] determined whether the acceleration exceeded a certain limit as the basis for judging instability,and calculated the probability of instability by the MC method.Using real statistics of the British population,Bocian et al.[14] obtained the statistical distribution of the pedestrian parameters (e.g.,gait length,step frequency,and body weight)used in the inverted pendulum model.In Bocian’s model,a lateral stability analysis of a footbridge in terms of probability was conducted,but the randomness of pedestrian excitation was not reflected through the stochastic process.In recent years,the authors [15,16] used the Lyapunov method based on the maximum Lyapunov exponent to judge whether the lateral vibration of the footbridge was stable,which avoided the large number of computations required by the numerical simulation method.
Structural stability analysis has experienced a history of static to dynamic stability [17,18].During the Euler time,static stability meant that the structure would not deviate from the initial equilibrium position under micro-disturbances,even if the critical load was reached.The Lyapunov theory is the representative for dynamic stability,which defined dynamic stability from the view of whether the trajectory of the dynamic system in the state space is sensitive to the initial disturbance [17,19–21].Both the classical static stability method and the dynamic stability method based on the Lyapunov method are qualitative analysis methods.For random vibrational stability,the Lyapunov-based method still only provides a binary result:stability with probability one (w.p.1)or instability with w.p.1,but not the quantitative probability of stability or instability.On the other hand,the structural stability can be attributed to the input–output equilibrium of energy.Therefore,in the field of stability analysis,there exist energy-based methods such as the Wang Ren energy criterion method [22] and the energy growth exponent method [23].However,these methods have specific limitations.The Wang Ren energy criterion method can only be used in conservative systems,and the energy growth exponent method can only be used in parametric excitation systems.Recently,Li et al.[24,25] proposed an energy-based method to identify vibrational stability based on the comparison of the input energy and the variation of intrinsic energy (IEVIE).The method can easily be used to establish a criterion for judging stability or instability in each random sample without setting a hypothesis that is as strict as the Lyapunov method.
Inspired by the IEVIE method,this study presents an IEVIE-SA method,combining the IEVIE method and the stochastic averaging (SA)method,by which the quantitative analysis of random vibrational stability was realized.Since the test results from Dallard et al.[3] demonstrated that the pedestrian’s lateral excitation depended on the velocity of the bridge,the improved Nakamura model (a velocity-dependent model)was used to describe the lateral nonlinear stochastic vibration of the footbridge.Additionally,the IEVIE method was used to determine the criteria for judging the stability of the improved Nakamura model.The SA method was used to establish a backward Kolmogorov equation corresponding to the improved Nakamura model.Then,the stability criterion was combined with the Kolmogorov equation to obtain the boundary condition of the first passage stability,whereby stability reliability was realized.
2 Lateral Vibration of Footbridge
2.1 Lateral Pedestrian Excitation
Generally,the lateral load per unit length exerted by pedestrians was defined as

wheremp(x)=Nmps/Lis the distributed mass withNpedestrians (massmpsof single person)on the bridge (Lof length),gis the acceleration of gravity,d0is the dynamic loading factor(a suggested value of 0.04 [11,26,27]),ρ0is the synchronization coefficient (a suggested value of 0.2 [9,28]),andG(˙y)is the velocity-dependent function describing the interaction between a pedestrian and footbridge vibration responses.In the original Nakamura model,a fractional form,including an absolute value,was used to describe the velocity-dependent function:G=˙y/(k3+|˙y|),which made it inconvenient to conduct an analytical deduction.The authors [15] proposed an improved Nakamura model (IN model)by replacing the fractional form with a polynomial form that could be conveniently used for the following analytical deduction:

The functionHis related to frequency detuning between pedestrian lateral walking frequencyωpand bridge frequencyωs.Synchronization of pedestrians is only possible when the frequency detuning is less than a certain small value.This kind of dependency can be simulated by a Gaussian curve.

Owing to intra-subject variability,ξ(t)is a narrow-band process.Ricciardelli et al.[29] used an improved treadmill to test the lateral pedestrian load.On the basis of the test data,they transformed the Fourier spectrum to the power spectrum and fitted the power spectrums using a Gaussian-curve.Although the Gaussian-curve can be used in numerical simulations through discretization,it is inconvenient for an analytical solution.An equivalent conversion method has
been previously proposed by the authors [15],in which the original PSD was transformed to a rational form:

whereσFis the square root of the area of the PSD around each harmonic,his the external excitation intensity factor,ξ(t)is the stochastic process with unit excitation intensity,ωpis the undisturbed gait frequency,as=0.9 andbs=0.043 are fitting quantities [13],δis the intensity of disturbance,B(t)is the Weiner process,and Φ denotes the uniformly distributed phase ∈(0,2π).On the basis of the above,the pedestrian excitation can be written as follows:

2.2 Equations of the Lateral Vibration of Footbridge
By using the simplest model,the modal vibration equation of the footbridge can be written as follows:

Hereωsis the bridge frequency,ζis the modal damping,andF(t)is

whereMsis the modal mass of the bridge,andϕ(x)is the mode shape.On the basis of Eqs.(5)and (7),F(t)can be unfolded as
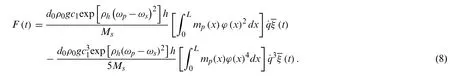
Set
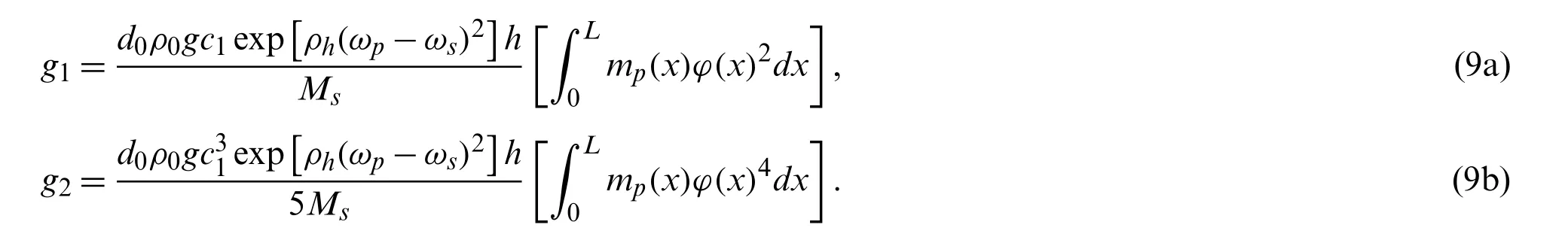
Then,Eq.(6)can be rewritten as
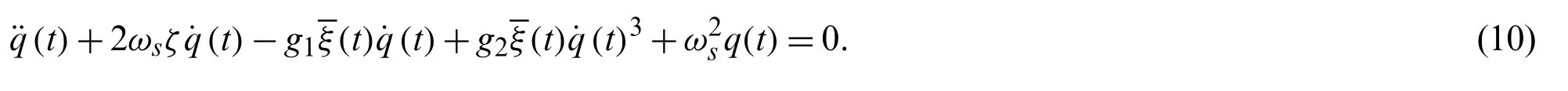
3 The Criterion for Judging Vibrational Stability Based on IEVIE
A general structural vibration system can be described as

For the system expressed by Eq.(11),the total input energyEI(t)imported into the structure can be written as

whereE0is the input energy contributed by the initial condition.The instantaneous work,Wext,done by the external force and the accumulated workWintdone by the internal reaction can be expressed as follows:

If the damping and inertial forces are regarded as external forces,then the equivalent external force is expressed asFext=p(t)−m¨z(t)−f1(˙z,t),and the internal reaction is expressed asFint(z)=f2(z,t).Importantly,Fext=Fint.Using these,Eqs.(13a)and (13b)can be rewritten as
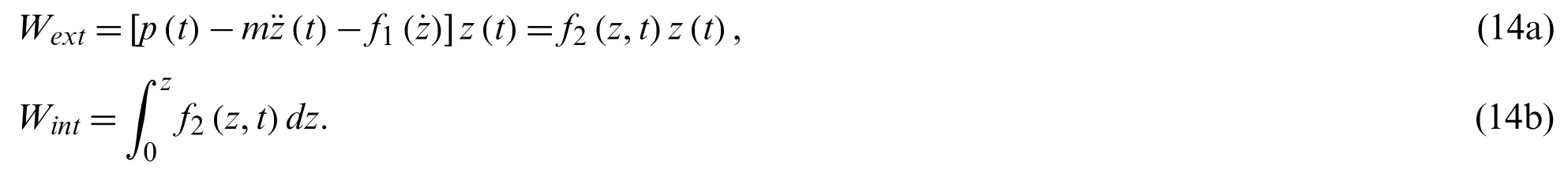
The total work done byFextandFintis

If the thermal energy is ignored,WΔ(t)is essentially the variation of intrinsic energy.In general,it can be assumed thatWΔ(t0)= 0,and the absolute value ofWΔ(t)is the absolute of the variation of intrinsic energyEΔ(t),which is also called the energy index given by
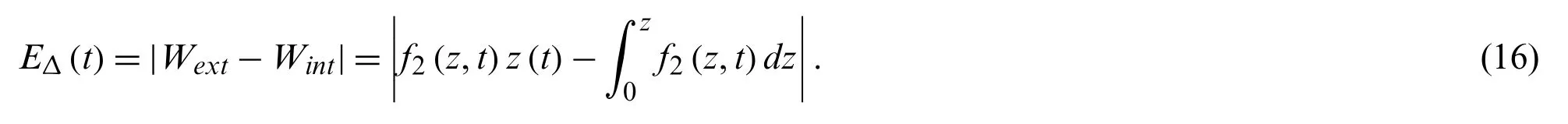
From previous research [24],based on IEVIE,vibrational stability at timetoccurred when the input energyEI(t)was balanced with the variation of intrinsic energy.By contrast,if the input energy was less than the variation of intrinsic energy,there must be other processes for absorbing energy in the system.These processes for absorbing energy could change the system from the original state to a new state (i.e.,the state of instability).Therefore,the criterion function for judging vibrational stability is established as

WhenS(t)<0,the vibration is instable; whenS(t)>0,the vibration is stable; andS(t)=0 is the limit of stability/instability.Back to Eq.(10)and set the initial condition toq(t0)=qu0and˙q(t0)=qv0,the input energyE0in the system of Eq.(10)has the following expression:

The expression ofEΔ(t)in the system of Eq.(10)can be written as

4 Stability Analysis Based on the IEVIE-SA Method
Li et al.[24] implemented the probabilistic analysis of structural vibrational stability by combining the IEVIE method with the probability density evolution method.However,this method required a large number of calculations.The main calculation can be approximately estimated as,np×TFD.npwas the number of discrete representative sample points in the probabilistic space of the probability density evolution method,which can be estimated as 200 in the normal case.TFDwas the time of each finite difference calculation.In the finite difference method,the space grids should be divided carefully to satisfy the convergence condition.In the normal case of structural vibration,if the explicit finite difference method with two-order accuracy was used,the conservative estimation of each calculation time was approximately 5 s.Therefore,it was roughly estimated that the completion time for a whole calculation was approximately 1000 s.Obviously,this number of calculations is too large,especially if performing a parameter variety analysis.Thus,a new method,the IEVIE-SA method,that combines the IEVIE and SA methods was proposed in this study.The SA method is a method of combining the stochastic averaging principle [20] with the Fokker–Planck–Kolmogorov Fokker–Planck–Kolmogorov (FPK)equation.After the stochastic averaging operation,the stochastic equations were considerably simplified.In the proposed method,the SA method was used to establish the backward Kolmogorov equation,and the stability criterion built by the energy method was treated as the boundary condition of the first passage reliability whereby dynamic reliability of vibrational stability was realized.The proposed method is a semi-analytical method that can greatly improve computational efficiency because it requires only one finite difference computation.
4.1 Stochastic Averaging Method
First,a conversion on the Eq.(10)was implemented as follows:

wheredΨ/dt=ω≈ωs.Combining Eqs.(10)and (20)resulted in

whereΛ=δB(t)+Φ.Using a detuning parameterε,one has

Herenandmare chose to be positive integers.By settingΔ=εΨ−(n/m)θ+Λ,Eq.(23)was rewritten as

By utilizing Itô’s differentiation rule,the Itô equations regardingAandΔwere obtained based on Eqs.(23)and (24)
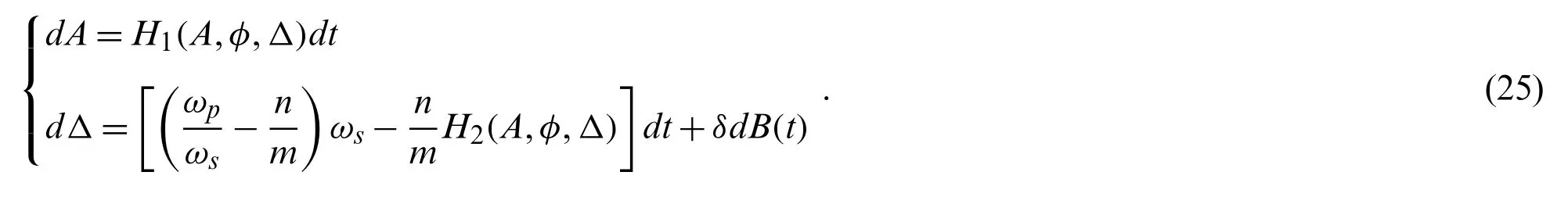
Given thatφis a fast variable when compared toAandΔ,an averaging operation ofφfrom 0 to 2πon Eq.(25)was implemented
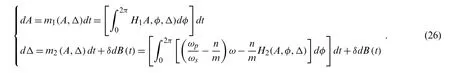
By considering the case of subharmonic resonance,n/m=2,Eq.(26)was rewritten as

4.2 First Passage Reliability of Vibrational Stability
From Eqs.(18)and (19),it was found thatS(t)was a slow variable because it belonged to the energy concept,indicating that an averaging method could also be applied toS(t).Therefore,a quasi-periodic averaging operation (i.e.,an averaging operation ofφfrom 0 to 2π)was implemented on Eq.(17)

After the averaging operation on Eq.(17),the simplified expression ofS(t)>0 was

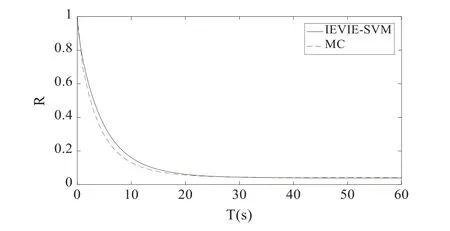
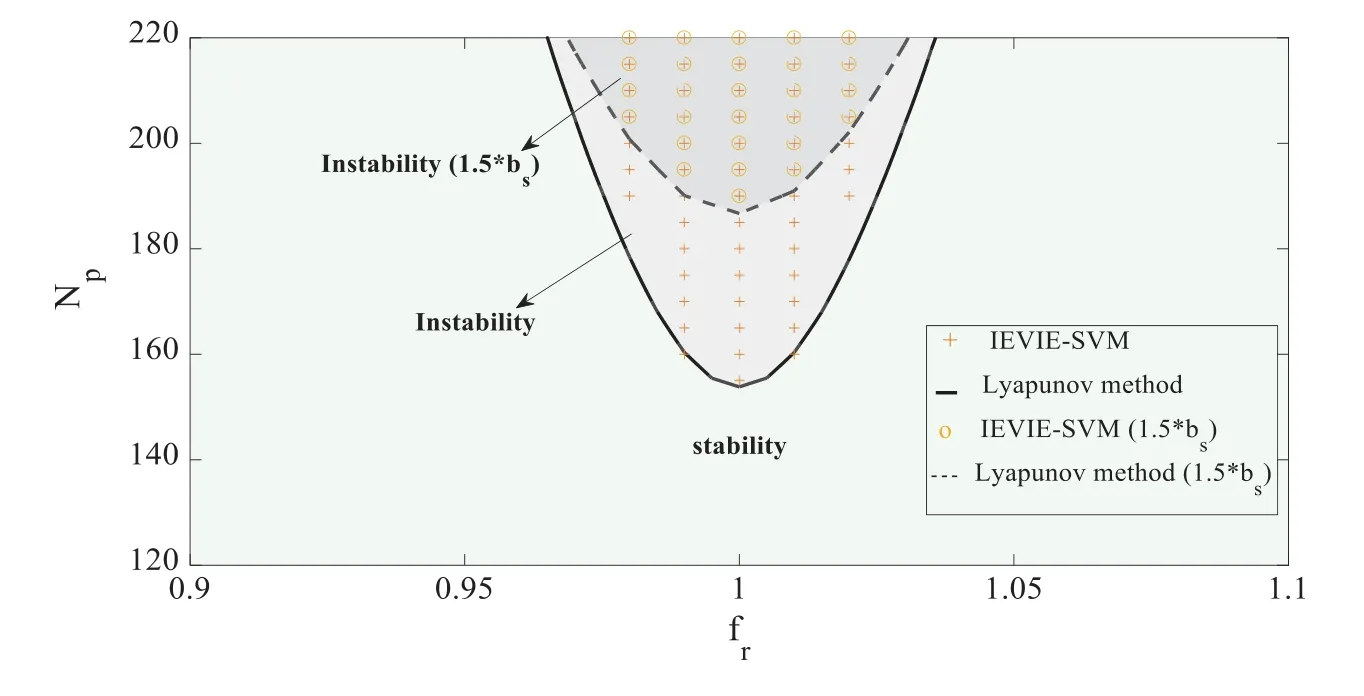
It should be noted that Eq.(28)is actually a deterministic averaging overT(equivalent to averaging overϕ),for the purpose to determining a critical value of vibration instability.This randomness has not been eliminated,which can be reflected inA(t)(see Eq.(25)).Eq.(29)denotes a first passage event ofA(t)with the boundary.On other hand,it can be known that the two-dimensional diffusion process [A(t),Δ(t)] was governed by Eq.(27).Since this study mainly focused on the resonance,the safety domain Ωsof vibrational stability was independent of the phase difference angleΔ,that is to say,Ωswas determined byAc(i.e.,Ωs={A(t) The corresponding conditional reliability can be defined as the probability of [A(τ),Δ(τ)]∈Ωsunder the given initial condition of [A0,Δ0] Subsequently,on the basis of Eq.(30),we have Letτ=t−t0; then,Eq.(32)can be rewritten as The initial condition of Eq.(33)is The boundary condition of Eq.(33)with regard toA0was The boundary condition of Eq.(33)with regard toΔ0satisfied the following periodic conditions: The partial differential equation of Eq.(33)generally had only numerical solutions,which could be solved by the finite difference method.In this study,the Peaceman–Rachford alternate direction implicit format of finite difference method is adopted (see Appendix A). The Millennium Bridge in London is a shallow suspension bridge with an 81 m north span,a 144 m central span,and a 108 m southern span.The first lateral mode of the central span was taken as the numerical example.According to the previous work [30],the structural parameters were given as follows:ωs=0.48×2π,ms=2000 kg/m,mps=70 kg,andζ=0.007. Fig.1 shows the time-varied stability reliability R(t)within T ∈[0,60s] when the number of pedestrians was Np= 180 and the frequency ratiofr(the ratio between walking frequency and doubled bridge frequency,i.e.,fr=fp/2fs)was 1.Stability reliability decreased rapidly with increasing time in the early stage but tended to converge in the later stage.The result of the MC method (106simulations)is also given in Fig.1,and it matched well with that of the proposed method,thereby verifying the effectiveness of the proposed method. Figure 1:Comparison between the IEVIE-SA and MC methods for the case of Np =180 and fr=1 Fig.2a shows the results when the number of pedestrians was Np=150 and the frequency ratio wasfr= 0.95,1,or 1.05.When the frequency ratio wasfr=1 (i.e.,the bridge frequency was half of the pedestrian walking frequency),stability reliability was very small,that is to say,the probability of vibration instability was very large (Pf=0.8987).When the frequency ratio was away fromfr=1,such as whenfr=0.95 orfr=1.05,stability reliability increased rapidly.These results showed that a 1/2 subharmonic (fp/2fsr=1)resonance played a key role in the vibration and may cause a dangerous situation.In addition,this may explain the large vibration in the central span of the Millennium Bridge because the fundamental frequency of the central span of the Millennium Bridge is approximately half of the pedestrian walking frequency.Fig.2b presents the results when the number of pedestrians was Np=180 and the frequency ratio wasfr= 0.95,1,and 1.05.The influence of the frequency on stability reliability was similar to that in Fig.2a.By comparing Figs.2a and 2b,it was shown that the number of pedestrians also had an important influence on stability reliability.The increase in the number of pedestrians led to a decrease in stability reliability,which will be discussed in detail in the following Figs.3a and 3b. Fig.3 shows stability reliability when the frequency ratio was fixed and the number of pedestrians was varied.Fig.3a corresponds to the case offr=0.95 and Np=[150,180,210],and Fig.3b corresponds to the case offr=1 and Np=[150,180,210].As shown in Fig.3a,stability reliability decreased with the number of pedestrians.When the number of pedestrians was relatively small (Np=150),its corresponding stability reliability was=0.8781,and when the number of pedestrians increased to Np=180,stability reliability decreased to=0.8092.In Fig.3b (fr=1),the weakening effect of increasing numbers of pedestrians on stability reliability was also observed. Figure 2:Stability reliability with a fixed number of pedestrians and the variant frequency ratio:(a) Np=150 & fr=[0.95,1,1.05]; (b)Np=180 & fr=[0.95,1,1.05] Figure 3:Stability reliability under a fixed frequency ratio and varying numbers of pedestrians:(a) fr=0.95 & Np=[150,180,210]; (b) fr=1 & Np=[150,180,210] To more clearly illustrate the influence of parameters on vibrational stability,Fig.4 shows a three-dimensional diagram of stability reliability under different combinations of pedestrian number and frequency ratios.The shape of the surface of R −Np−frappeared as a “valley.”When the frequency ratio is away fromfr=1,stability reliability was large and even (i.e.,two flat areas on the top of the valley); when the frequency ratio was close tofr=1,stability reliability decreased sharply (i.e.,cliffs on both sides of the valley); and when the frequency ratio was almostfr=1,stability reliability reached a minimum (i.e.,the middle bottom of the valley).It clearly showed that the frequency had a dominant effect on vibrational stability,and the number of pedestrians had a relatively smooth effect on vibrational stability.Additionally,the effect of frequency on vibrational stability depended on the number of pedestrians.The frequency range at the bottom of the valley (frequency corresponding to low reliability)became wider as the number of pedestrians increased.In other words,as the number of pedestrians increased,the probability points inducing a high probability of instability also increased.The effect of the number of pedestrians on vibrational stability was also related to the frequency.When the frequency ratio was far fromfr=1,the effect of the number of pedestrians on vibrational stability was small,but when the frequency ratio was nearfr=1,an increase in the number of pedestrians significantly reduced stability reliability. Of note,compared with the traditional Lyapunov method that can only obtain two qualitative results (stability or instability),the quantitative results obtained by the proposed method contained more information and were more practical,especially for designers. Figure 4:Three-dimensional graph of R −Np −fr The influence of randomness on the system stability is also investigated through the parameter analysis ofbsin Eq.(4),since the intensity of random disturbanceδhas a monotonic relationship withbs(increasingbsis equal to strengthening the random disturbance).Figs.5a and 5b correspond to the case ofbs=[0.023,0.043,0.063] &fr=1 andbs=[0.023,0.043,0.063] &fr=0.95,respectively.It can be found that the influence ofbson the stability reliability R depends on the distribution offr:Rt=60increases along withbswhenfr=1,while decreases with the increase ofbswhenfrfar from 1 (fr=0.95). Figure 5:Stability reliability with different combinations of bs and fr: bs = [0.023,0.043,0.063](a) fr=1; (b) fr=0.95 To further verify the effectiveness of the proposed method,the Lyapunov method based on the maximal Lyapunov exponent was implemented for comparison.Performing a linear operation about the derived coefficients in Eq.(27)atA=0 gave With γ=lnA,Eq.(37)was rewritten as Since Δ(t)was the Ergodic Markov process within [0,2π],its invariant measure was the stationary probability density function p(Δ)that had the following stationary FPK equation: In addition,p(Δ)satisfied the periodic boundary condition p(Δ)= p(Δ + 2π)and the probability normalization condition.The solution of Eq.(39)was given as where A0and Δ0are the initial values.On the basis of Eqs.(40)and (41),the maximal Lyapunov exponent λmaxwas The stability of the trivial solution of Eq.(38)was determined by the sign of λmax.The trivial solution of Eq.(38)was stable w.p.1 when λmax<0 and unstable w.p.1 when λmax>0.Thus,the critical boundary between stability and instability could be approximated by λmax=0.This kind of stability definition given by the sign change of the maximum Lyapunov exponent is also called stochastic D-bifurcation. Unlike the traditional Lyapunov definition of random vibrational stability,we can simply give the definition of random vibrational stability according to the probability obtained from IEVIESA.If the following equation was satisfied, the system was stable with probability Rlim,or the system was unstable with probability 1 −Rlim. Fig.6 compares the results of the Npand frspaces of the proposed method and the Lyapunov method based on the maximal Lyapunov exponent λmax.The light gray and light green areas are the areas of instability and stability,respectively,that were determined by the Lyapunov method.The black curve is the critical boundary between instability and stability.The yellow“+” denotes the points of Np and frobtained from the IEVIA-SA method,which were stable with probability less than 10% (or unstable with probability greater than 90%).Since probability greater than 90% indicated very high probability of instability,it was conservatively regarded as approximately unstable.From Fig.6,all points that were unstable with probability greater than 90% were located in the area of instability determined by the Lyapunov method.Additionally,the outer contours of these points were consistent with the critical boundaries obtained by the Lyapunov method.These well-matched results verified the effectiveness of the IEVIE-SA method.From another perspective,the limitation of the Lyapunov method was also revealed because it only obtained a binary qualitative result (stability or instability)without any intermediate values.The judgment of stability or instability was too absolute and may be relatively unreasonable in practice.In contrast,the IEVIE-SA method proposed in this study used probability to represent the degree of vibrational stability (or instability),and it is more practical and persuasive.Moreover,the influence from randomness is also reflected in Fig.6.When the value ofbsis enlarged to 1.5bs,the instability area with points those were unstable with probability greater than 90% is obviously reduced (the critical Npneeded to trigger instability increases),which means the increase of random disturbance is beneficial to the stability.This conclusion can also be found in the result obtained by Lyapunov method. Figure 6:Comparison of the IEVIE-SA and Lyapunov methods This study established a framework to efficiently and quantitatively analyze the stability reliability of the lateral vibration of a footbridge.The IN model was used to describe the lateral vibration of footbridges,considering the correlation between pedestrian excitation and bridge vibration,and the randomness of pedestrian excitation.The IEVIE method based on the comparison of input energy and the variation of intrinsic energy was used to establish the judging criteria to identify vibrational stability.In addition,the SA method was used to establish the stochastic Itô equation with slow variables as well as the corresponding backward Kolmogorov equation for condition reliability.Subsequently,the stability criterion established by the IEVIE was combined and treated as the boundary condition of the first passage reliability within the backward Kolmogorov equation,by which the first passage reliability of vibrational stability was obtained.The main results were as follows: 1)The proposed method was successfully applied to the central span of the Millennium Bridge,and its validity was verified by comparing it with the MC and traditional Lyapunov methods. 2)The frequency had an important influence on the lateral vibrational stability of the footbridge.When the walking frequency was equal to the doubled bridge frequency,stability reliability had an extremely small probability.This may explain the large vibration of the central span of the Millennium Bridge,which has a fundamental frequency that is half of the pedestrian walking frequency.The number of pedestrians also affected the lateral vibrational stability of the footbridge.Stability reliability decreased with increasing numbers of pedestrians.When the number of pedestrians reached 180 under the worst case (fr=1),the vibration was unstable with a probability of 96%,which was consistent with the on-site observed result [30] (the critical number of pedestrians that triggered the unstable vibration was approximately 170)and the results from other researchers [10,13]. 3)Compared to the number of pedestrians,the frequency had a more dominant influence on the lateral vibrational stability of the footbridge.However,the influence from the number of pedestrians and the frequency were coupled:the greater the number of pedestrians,the more frequency points that could cause a large probability of instability.On the other hand,the closer the frequency ratio was to 1,the greater the change in stability reliability caused by the number of pedestrians. 4)Compared to the traditional Lyapunov method,the proposed method could conduct quantitative analysis of the random vibrational stability of the footbridge,which is more practical and reasonable.Another advantage of the proposed method is that it uses the stochastic averaging method to simplify the stochastic equations,which greatly reduces the number of calculations. Nevertheless,the proposed method also has some limitations.First,the IN model used in this study was essentially a backstepping model and did not guarantee that the full mechanism of the lateral vibration of the footbridge was revealed.In the future,more valuable data should be collected to further refine this model.Second,in this study,only three parameters were analyzed:the number of pedestrians,the frequency ratio,and the intensity of random disturbances.There may be other key parameters that also have an important influence on the lateral vibrational stability of the footbridge.Therefore,more detailed studies with respect to parametric analysis are needed.Third,for the sake of simplicity,this paper considers only the first-order mode,thus the suitability of the proposed method in another adjacent mode (e.g.,the lateral second mode with a frequency around 1 Hz in the central span of the Millennium Bridge)cannot be guaranteed.Moreover,it cannot exclude the possibility that the forced resonance and subharmonic resonance may act simultaneously to drive the large lateral vibration,which is worth studying in the future.Finally,due to the limited data,this study only used the Millennium Bridge as a numerical example.It is necessary to collect information from other footbridges as references to further verify the generality of the proposed method. Funding Statement:This research was supported by the National Natural Science Foundation of China (No.51608207)and the Natural Science Foundation of Guangdong Province,China (No.2019A1515011941). Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study. Appendix A:Peaceman–Rachford’s Alternate Direction Implicit Format The two-dimensional partial differential Eq.(33)can be solved using the finite difference method.When the convergent condition is strict,the backward Euler and Crank–Nicolson schemes can be used because they are unconditionally stable.However,in these two methods,the difference equations on each time layer will have a huge number,and they are no longer tridiagonal linear equations.The calculations for solving such equations are unacceptable.In this study,the Peaceman–Rachford’s alternate direction implicit format (PR ADI)was used,and PR ADI was unconditionally stable and could be solved using the chasing method.For convenience,R(A0,Δ0,t)in Eq.(33)was abbreviated to R.In addition,the time step was set as dt = t/s,andtn=ndt,0 ≤n≤s.The space steps with regard toAandΔwere set ashAandhΔ,respectively,resulting inA0,i=A0,min+(i−1)hA,1 ≤i≤kandΔ0,j=Δ0,min+(j−1)hΔ,1 ≤j≤m.To establish the one-dimensional implicit format,the derivative with regard toA0was replaced by the unknown center difference quotient of R on then+1th time layer,and the derivative with regard toΔ0was replaced by the known center difference quotient of R on thenth time layer.The resulting equations were only implicit in the direction ofA0,which was easier to solve by using the chasing method.For the sake of symmetry,the above steps were repeated on the next time layer,on which theΔ0direction was implicit and theA0direction was explicit.By doing this,the two adjacent time layers could be combined to form a difference format.The corresponding PR ADI format of Eq.(33)was as follows: wherendenotes the time mesh step index andiandjrepresent the space mesh step indices.Other symbols were defined as follows: By settingλvalues as Eq.(A1)could be rearranged as The matrix form corresponding to Eq.(A1)had the following form: By combining the initial condition (Eq.(34))and the boundary conditions (Eqs.(35)and (36))and using the chasing method to solve Eq.(A4),the solution ofwas easily obtained.Then,Eq.(A2)was rearranged as The matrix form corresponding to Eq.(A5)can be expressed as Like that for Eq.(A4),the chasing method can be used to solve Eq.(A6)to obtain the result of then+1th time layer.It can be seen that the calculation ofconsisted of two steps,and each step was only implicit in one direction.By repeating the above steps on the following time layers,the final result of the last time layer could be obtained.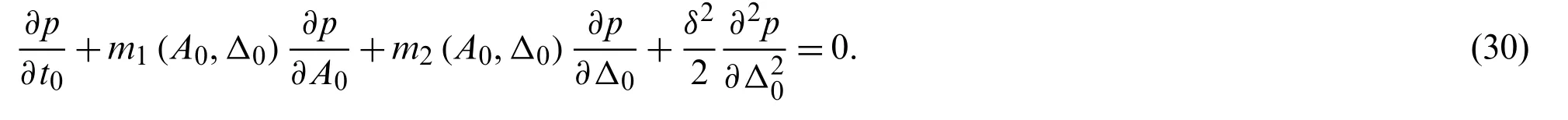
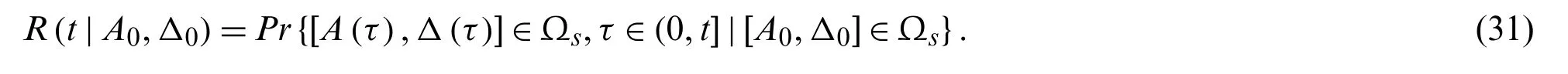
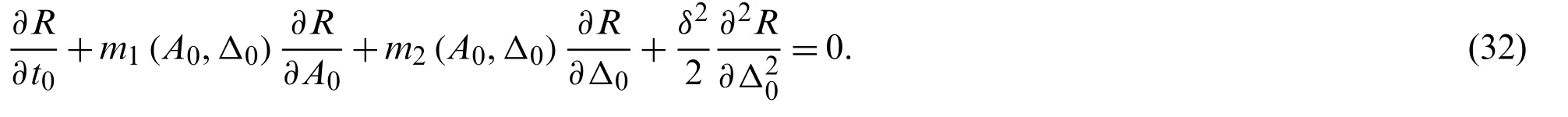
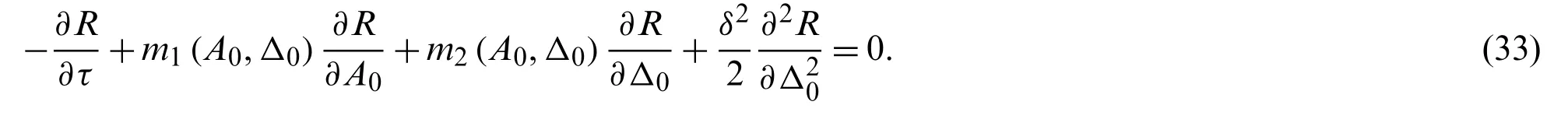



5 Application of the IEVIE-SA Method to the London Millennium Bridge
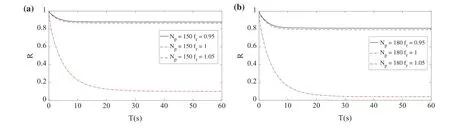
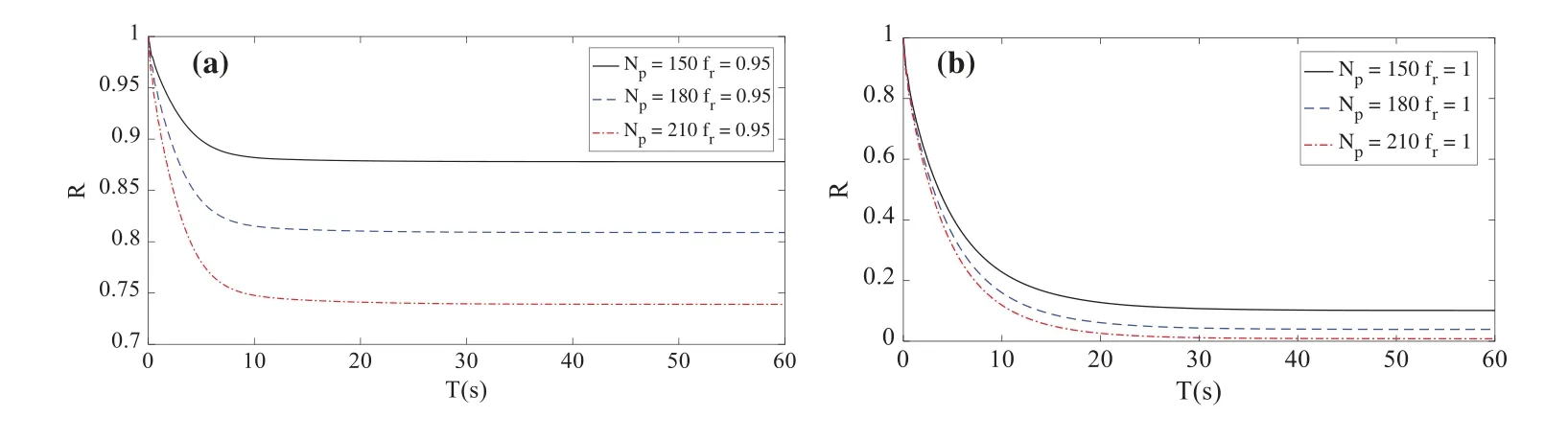
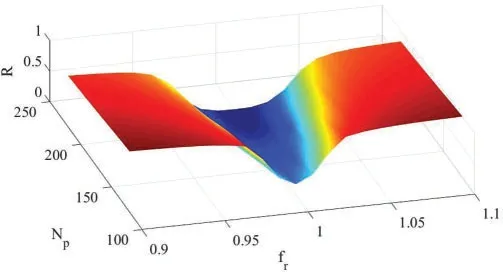
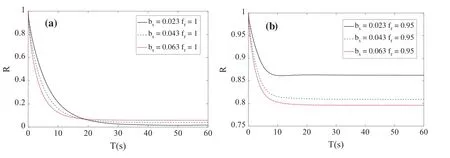
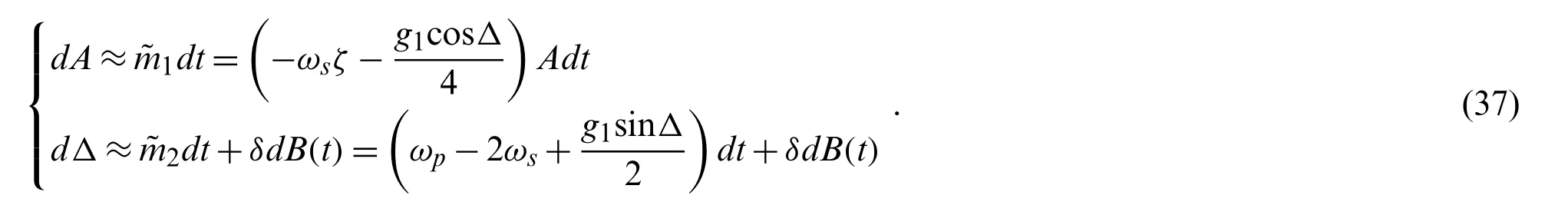


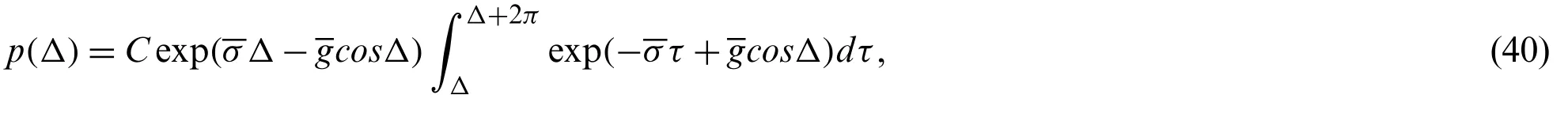

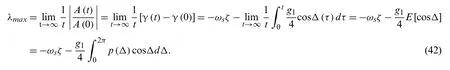

6 Conclusions



 Computer Modeling In Engineering&Sciences2021年8期
Computer Modeling In Engineering&Sciences2021年8期
- Computer Modeling In Engineering&Sciences的其它文章
- A Knowledge-Enhanced Dialogue Model Based on Multi-Hop Information with Graph Attention
- MRI Brain Tumor Segmentation Using 3D U-Net with Dense Encoder Blocks and Residual Decoder Blocks
- A Contemporary Review on Drought Modeling Using Machine Learning Approaches
- Multi-Disease Prediction Based on Deep Learning:A Survey
- Multi-Material Topology Optimization of Structures Using an Ordered Ersatz Material Model
- Intelligent Segmentation and Measurement Model for Asphalt Road Cracks Based on Modified Mask R-CNN Algorithm
