基于平滑变结构-卡尔曼滤波的MIMU/BDS组合导航技术
李灿 沈强 秦伟伟 段志强 汪立新

摘 要: 为了提高模型不准确、大扰动等情况下MIMU/BDS组合导航精度,提出了平滑变结构-卡尔曼组合滤波的信息融合方法。介绍了坐标转换方法,建立了组合导航系统的状态空间方程和观测方程。为了防止老旧观测数据引起算法发散,在卡尔曼滤波算法中融入随残差自适应变化的渐消因子,从而构造了自适应卡尔曼滤波算法。将卡尔曼滤波的精度优势与平滑变结构滤波的鲁棒性优势融合,提出了平滑变结构-卡尔曼组合滤波算法。经仿真验证,在模型不准确、大扰动等情况下,组合算法的位置融合误差和速度融合误差均小于卡尔曼滤波和自适应卡尔曼滤波算法;经跑车试验验证,在卫星遮挡情况下,组合导航系统的位置融合精度和速度融合精度仍然较高,实现了卫星可观数量不足情况下的精确导航。
关键词:MIMU/BDS组合导航;模型不准确;自适应渐消因子;平滑变结构滤波;组合滤波算法
中图分类号:TJ765; V448 文献标识码: A 文章编号:1673-5048(2021)03-0051-08
0 引 言
不同的导航手段中,北斗卫星的定位精度高、实时性好,但是卫星极易被遮挡;MIMU可以提供全部导航信息,且不受任何外界干扰,但是其导航误差随时间积累。将北斗卫星与MIMU导航进行信息融合,实现MIMU/BDS的优势互补,可以提高导航定位的连续性和定位精度[1],具有重要的研究价值。
多源传感器信息融合技术相比于单一传感器系统,具有更高的定位精度、更高的定位稳定性,兼具了各子导航系统的优势。信息融合算法可大致分为3类:基于概率模型的融合算法、基于参数识别的融合算法、新型信息融合算法。具体地讲,信息融合算法包括贝叶斯估计法[2]、物理建模法、卡尔曼滤波算法[3]、神经网络算法[4]、支持向量机、因子图法[5]等。基于参数识别的融合算法主要包括卡尔曼滤波及其改进算法、平滑变结构滤波、粒子滤波[6]等,其中卡尔曼滤波是一种最优状态估计算法,信息融合精度较高,但是当出现模型不准确、外界扰动较大时,卡尔曼滤波算法容易发散,即算法的鲁棒性较差[7]。平滑变结构滤波是一种次优滤波方法,其滤波精度略低于卡尔曼滤波,但是在应对模型不准确、大扰动等情况时具有较好的鲁棒性[8]。本文为了兼顾滤波的精度和鲁棒性,将卡尔曼滤波的精度优势和平滑变结构滤波的鲁棒性优势进行融合,提出了AKF和SVSF的组合滤波方法,有效提高了模型不准确、大扰动等异常情况下的组合导航精度和鲁棒性。
1 MIMU/BDS组合导航建模
1.1 常用坐标系定义
MIMU在车辆上的安装方式为捷联方式,加速计与陀螺仪的测量信息经过坐标变换才能获得车辆的导航信息。求解过程中用到的坐标系包括地心坐标系(i系)、地球坐标系(e系)、导航坐标系(n系)和载体坐标系(b系),在此对各坐标系的定义方法进行明确。
地心坐标系(i系):原点位于地球中心O,Xi是地球公转的黄道平面与赤道平面的交线, Yi按右手规则定义,Zi的方向与地球的极轴方向一致。
地球坐标系(e系):原点位于地球中心,坐标系与地球固连。其中Ze沿地球极轴方向,Xe沿格林尼治子午面与地球赤平面的交线,Ye根据右手定则确定。地球坐标系相对于惯性坐标系绕Zi以角速度Ω转动。
导航坐标系(n系):原点位于车辆质心位置,本文使用东北天坐标系作为导航坐标系,即Xn,Yn,Zn分别为东向、北向和天向。
载体坐标系(b系):Xb,Yb,Zb分别为载体坐标系的横滚轴、俯仰轴和偏航轴。
坐标系间的变换通过平移变换和旋转变换实现,其中旋转变换使用欧拉角法,即通过3次旋转实现坐标系间的姿态重合。由于欧拉角法已经成熟,这里不再详细介绍,将坐标系A向坐标系B间的变换矩阵记为CBA。
2.3 平滑变结构-卡尔曼组合滤波
分析式(19)可知,平滑有界层宽度跟模型不确定性、系统噪声、量测噪声、观测误差等直接相关,因此, 其可以用来衡量模型不确定性和噪声大小。本文将平滑变结构滤波与卡尔曼滤波组合的思路为:设置一个有界层ψlim,当ψk+1<ψlim时,说明系统模型较为准确、噪声较小,为了保证滤波精度,使用最优状态估计方法——卡尔曼滤波;当ψk+1≥ψlim时,说明系统模型误差较大、噪声较大,为了保证滤波稳定性和鲁棒性,使用次优状態估计方法——平滑变结构滤波。组合算法示意图如图2所示。
平滑变结构-卡尔曼组合滤波(记为SVSKF)的迭代过程为
(1) 计算状态向量一步预测值,观测向量一步预测值、一步预测误差方差阵、量测误差;
(2) 计算平滑有界层宽度,如式(19);
(3) 若ψk+1<ψlim,则使用AKF增益KAKFk+1;若ψk+1≥ψlim,则使用SVSF增益KSVSFk+1;
(4) 计算后验状态估计值,更新滤波误差方差阵、后验量测估计值、后验量测误差,如式(20)。
需要说明的是,有界层ψlim是人为设置,具体方法为:以状态量εE为例,根据εE的实际变化范围,设置εE有界层的可取范围,其中可取范围略大于实际变化范围。而后以滤波误差为指标,得到εE有界层取不同值时的滤波误差,以图形方式画出滤波误差随εE有界层取值的变化趋势,选择滤波误差最小时对应的εE有界层值为最终确定的εE有界层取值。
3 试验验证
为了验证平滑变结构-卡尔曼组合滤波算法在系统受到大扰动、模型不准确、卫星数量不足等情况的鲁棒性、稳定性和导航精度,本文设计了2组仿真试验和1组跑车试验。
3.1 仿真试验一
設置系统仿真参数:车辆初始位姿参数设置为经度34°,纬度108°,高度380 m,水平姿态角0°,航向角0°;初始误差参数设置为定位误差10 m,速度误差0.1 m/s,姿态角初始误差1°,航向初始误差2°;惯性器件参数设置为陀螺仪常值漂移10 (°)/h,角度随机游走1 (°)/h,加速度计零偏10-4g,随机游走误差4×10-5g/h,更新频率100 Hz; BDS接收机参数设置为定位误差10 m,测速误差0.1 m/s,数据更新频率1 Hz。
场景设置:假设车辆起始时刻以5 m/s的速率作匀速直线运动,之后以1 m/s2加速度行驶100 s,最后匀速行驶。在对准过程中,忽略高度变化。设定1 200 s的“S”型标准轨迹,如图3所示。
在卫星接收机收星稳定且大于4颗的情况下验证算法的组合导航精度,为了说明该算法的优劣性,采用AKF算法、传统KF算法和本文的SVSKF算法融合效果进行对比,结果如图4所示。
由图4可知,在卫星接收机收星稳定且大于4颗的情况下,SVSKF和AKF算法的位置融合误差、速度融合误差相差不大,位置融合误差在2 m内,速度融合误差在0.1 m/s内。而KF算法的位置融合误差和速度融合误差较大,位置最大误差为10 m,速度最大误差为1 m/s。这是因为图3的标准轨迹中存在大角转弯的情况,此时存在非线性耦合情况,使KF算法的导航信息融合精度较差,而AKF和SVSKF算法由于增益可以随新息的大小进行自适应,使算法快速收敛,因此导航精度较高。
3.2 仿真试验二
在仿真试验二中,将标准轨迹改为直线,其余的系统参数和场景设置与3.1节一致。
在1 200 s仿真过程加入3种扰动量:(1)在400~460 s期间设置模型不准确扰动,方法为在状态转移矩阵对角元素中随机选择3个元素,施加其自身幅值10%的随机干扰;(2)在600~660 s期间设定大的白噪声,即将系统噪声和量测噪声的幅值均调大3倍;(3)在1 000~1 020 s期间设定可观测卫星为3颗。为了说明该算法的优劣性,采用AKF算法、传统KF算法和本文的SVSKF算法融合效果进行对比,结果如图5所示。
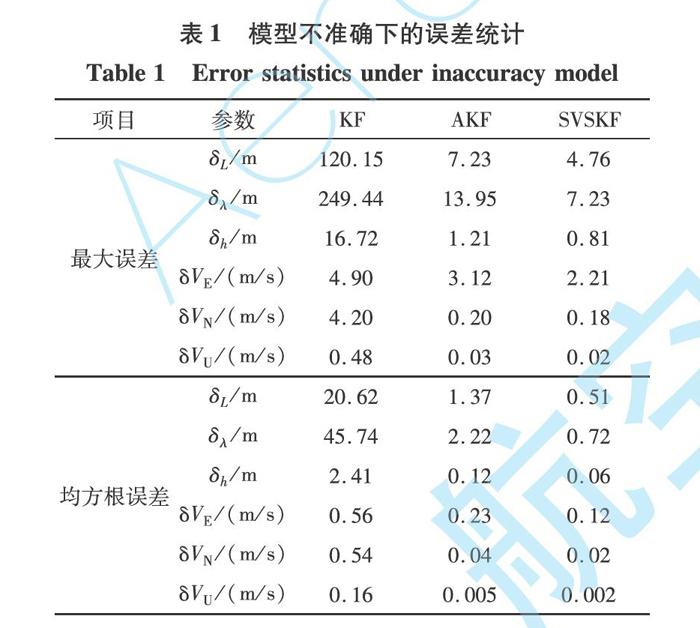
由图5可以直观看出,3种扰动下KF算法的位置融合误差和速度融合误差均较大,无法应用于实际。而AKF和SVSKF算法融合精度较高,且SVSKF算法的融合精度略高于AKF算法。以模型不准确为例,在统计模型不准确情况下,传统KF,AKF,SVSKF三种算法的位置融合误差和速度融合误差如表1所示,其中均方根误差的统计时间为400~600 s。
分析表1中数据可知,在模型不准确的情况下,KF算法的位置融合误差和速度融合误差均较大,AKF算法的融合误差次之,SVSKF算法的位置融合精度和速度融合精度均较高。这是因为模型不准确导致的状态估计值与实际值偏差较大,KF算法的信息融合能力有限,使得融合误差较大。AKF算法可以根据观测值残差自适应调整遗忘因子,增强算法的收敛性,使融合误差迅速减小,快速恢复到期望值附近。SVSKF算法能够根据系统状态的变化在AKF算法增益和SVSF算法增益间切换,兼具AKF算法的精确性和SVSF算法的鲁棒性,因此融合精度最高。
3.3 跑车试验
本次试验目的为验证SVSKF算法在实际跑车过程中的信息融合精度。选取实际的组合系统作为试验对象进行跑车试验。北斗时代生产的BDST-MGI760-MIMU微机械惯性测量装置详细参数如表2所示。
MIMU数据更新率为100 Hz,采样周期为0.01 s。BDS采样频率为1 Hz,采样周期为1 s。卫星接收机利用MIMU自带的BDS卫星接收模块,采用双天线差分定位,试验装置如图6(a)~(b)所示。车辆的参考位置使用高精度的激光惯组/GPS组合导航系统,如图6(c)所示。
组合导航试验运动载体为汽车,在校园灌木丛较多的区域进行跑车试验,主要验证卫星信号受干扰情况下组合定位系统的跟踪情况。汽车的运行轨迹如图7所示。
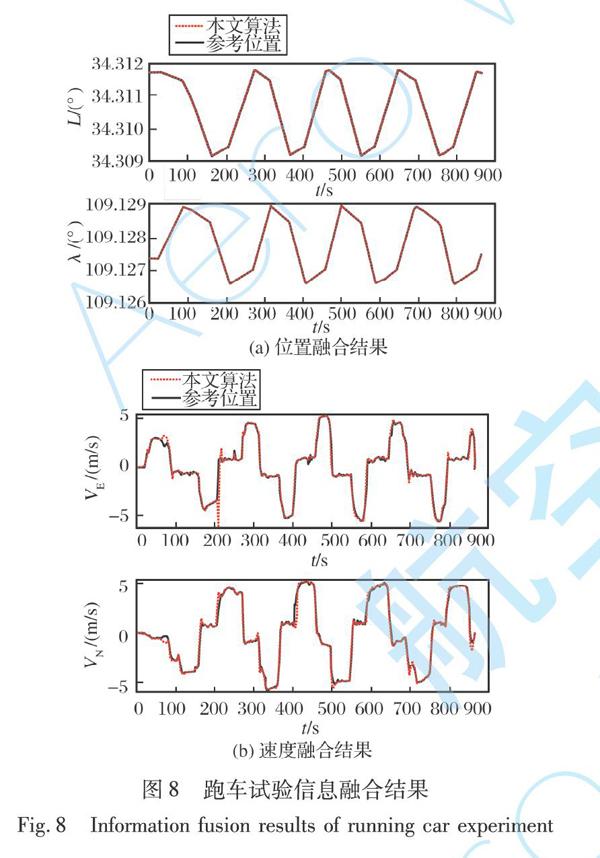
MIMU/BDS组合定位系统运行10 min后采集数据,路况覆盖了卫星正常和卫星受干扰的情况,起点处具有较大的灌木丛区域和建筑群,卫星观测信号弱;终点在开阔区域,卫星定位精度高。为了增强试验可信性,车辆围绕设定轨迹跑4圈,采用本文算法得到的位置和速度如图8所示。由于车辆在平地上试验,因此对高度融合信息不进行分析与讨论。
分析图8(a)可知,在整个试验过程中汽车位置的经度和纬度信息融合精度较高,融合位置能够精确地定位到参考位置,且在卫星信号良好与被遮挡的切换过程中,位置融合信息也能够平稳过渡,波动极小。说明在卫星可观测数量不足的情况下,SVSKF组合滤波方法依然能够有效地进行信息融合,得到较高精度的位置信息。分析图8(b)中东向速度误差和北向速度误差可知,速度融合信息能够精确地跟踪参考速度,东向最大瞬时速度误差为1.2 m/s,均方根误差为0.02 m/s;北向最大瞬时速度误差为0.3 m/s,均方根误差为0.01 m/s,即速度融合误差和波动均较小。这是因为组合滤波器能根据状态量的估计误差自主选择滤波方法,当状态量误差较小,出现在有界层范围内时,使用残差自适应卡尔曼滤波,保证较高的滤波精度;当状态误差较大,出现在有界层范围外时,使用平滑变结构滤波,提高算法的鲁棒性。综合仿真结果和跑车试验结果可知,SVSKF组合滤波方法能够有效解决大扰动、模型不准确和卫星可观测数量不足等情况下的MIMU/BDS组合导航的精度和鲁棒性问题。
参考文献:
[1] 陈德潘, 陈帅, 樊龙江, 等. MIMU/CSAC/BDS组合导航微系统的硬件设计[J].航天控制, 2018, 36(3): 71-78.
Chen Depan, Chen Shuai, Fan Longjiang, et al. The Hardware Design of MIMU/CSAC/BDS Integrated Navigation Micro System [J]. Aerospace Control, 2018, 36(3): 71-78.(in Chinese)
[2] 戴海发, 卞鸿巍, 马恒, 等. 全源定位与导航的统一理论框架构建[J].导航定位与授时, 2018, 5(6): 9-16.
Dai Haifa, Bian Hongwei, Ma Heng, et al. Unified Theoretical Framework Construction of All Source Positioning and Navigation [J]. Navigation Positioning and Timing, 2018, 5(6): 9-16.(in Chinese)
[3] 刘军, 刘克诚, 田甜, 等. 基于自适应卡尔曼滤波算法的紧组合导航系统的研究[J]. 电子测量技术, 2019, 42(5): 52-55.
Liu Jun, Liu Kecheng, Tian Tian, et al. Research on Tight Integrated Navigation System Based on Adaptive Kalman Filter Algorithm [J]. Electric Measurement Technology, 2019, 42(5): 52-55.(in Chinese)
[4] 刘宇, 惠鸿飞, 路永乐, 等. 基于遗传算法优化神经网络的多源信息融合室内定位方法[J]. 中国惯性技术学报, 2020, 28(1): 67-73.
Liu Yu, Hui Hongfei, Lu Yongle, et al. Multi-Source Information Fusion Indoor Positioning Method Based on Genetic Algorithm to Optimize Neural Network [J]. Journal of Chinese Inertial Techno-logy, 2020, 28(1): 67-73.(in Chinese)
[5] 尹慧琳, 伍淑莉, 王亚伟, 等. 基于层次因子图的智能车环境感知和态势认知模型[J]. 控制与决策, 2020, 35(10): 2528-2534.
Yin Huilin, Wu Shuli, Wang Yawei, et al. An Intelligent Vehicle Environment Perception and Situation Cognition Model Based on Hierarchical Factor Graph [J]. Control and Decision, 2020, 35(10): 2528-2534.(in Chinese)
[6] 薛丽, 潘欢, 魏文辉. 自适应高斯粒子滤波在导航中的应用[J]. 计算机仿真, 2020, 37(1): 121-125.
Xue Li, Pan Huan, Wei Wenhui. Adaptive Gaussian Particle Filtering for Navigation [J]. Computer Simulation, 2020, 37(1): 121-125.(in Chinese)
[7] 蔡體菁, 颜颖, 王新宇. 捷联航空重力测量中的卡尔曼滤波[J]. 压电与声光, 2019, 41(3): 436-439.
Cai Tijing, Yan Ying, Wang Xinyu. Kalman Filtering of Strapdown Airborne Gravity Measurement [J]. Piezoelectrics & Acoustooptics, 2019, 41(3): 436-439.(in Chinese)
[8] 施常勇, 张丽敏. 平滑变结构滤波在航天器组合导航中的应用[J].中国惯性技术学报, 2017, 25(4): 478-482.
Shi Changyong, Zhang Limin. Application of SVSF in Spacecraft Integrated Navigation System [J]. Journal of Chinese Inertial Technology, 2017, 25(4): 478-482.(in Chinese)
[9] Susi M, Borio D. Kalman Filtering with Noncoherent Integrations for Galileo E6-B Tracking[J]. Navigation, 2020, 67(3): 601-618.
[10] 薛海建, 郭晓松, 周召发.基于自适应多重渐消因子卡尔曼滤波的SINS初始对准方法[J].系统工程与电子技术, 2017, 39(3): 620-626.
Xue Haijian, Guo Xiaosong, Zhou Zhaofa. SINS Initial Alignment Method Based on Adaptive Multiple Fading Factors Kalman Filter [J]. Systems Engineering and Electronics, 2017, 39(3): 620-626.(in Chinese)
MIMU/BDS Integrated Navigation Technology Based on
Smooth Variable Structure-Adaptive Kalman Filter
Li Can, Shen Qiang*, Qin Weiwei, Duan Zhiqiang, Wang Lixin
(Rocket Force University of Engineering, Xian 710025,China)
Abstract:
In order to improve the accuracy of MIMU/BDS integrated navigation with uncertain models and large disturbances, a smoothing variable structure-Kalman combined filter information fusion method is proposed. The coordinate transformation method is introduced, and the state space equation and the observation equation of the integrated navigation system are established. In order to prevent the algorithm divergence caused by the old observation data, the adaptive fading factor which varies with the residual error is incorporated into the Kalman filter algorithm, and the adaptive Kalman filter algorithm is constructed. Combining the accuracy advantage of Kalman filter with the robustness advantage of smooth variable structure filter, a smooth variable structure-Kalman combined filter algorithm is constructed. It is verified by simulation that location and speed fusion error of combined algorithm are smaller than Kalman filter and adaptive Kalman filter under the condition of uncertain model and large disturbances. The experiment shows that location fusion accuracy and speed fusion accuracy are also high under the condition of satellite occlusion, which means the accurate navigation with insufficient number of satellites is achieved by utilizing the combined filter algorithm.
Key words: MIMU/BDS integrated navigation; uncertain model; adaptive fading factor; smooth variable structure filter; combined filter algorithm
收稿日期:2020-10-27
項目基金:陕西省自然科学基础研究计划项目(2020JQ-491; 2020JM-357)
作者简介:李灿(1989-),男,山东兖州人,硕士,助教,研究方向为惯性系统及仪器。
通讯作者:沈强(1989-),男,山东高密人,博士,讲师,研究方向为惯性系统及仪器。

