一种探月返回轨迹大气层内外联合规划制导算法研究

尤志鹏，杨 勇，刘 刚，郑宏涛

（中国运载火箭技术研究院，北京，100076）

0 引 言

月球探测技术是当前深空探测的重点领域，当前对月球返回轨道的研究得到广泛的关注。通常基于双二体模型，在月球影响球边缘进行轨道拼接，从而形成完整的大气层外返回轨道。轨道设计过程中对再入过程考虑较少，往往对飞行器可用过载等要求较高且再入过程中往往需要较大横程能力来调整状态偏差。

各国学者对返回轨迹及其中途修正技术已经有了较为深入的研究。美国早在阿波罗登月时期就对月地返回轨道开展了深入研究[1,2]，但进行了假设，模型较为简单。Hui Yan 等[3]进一步考虑了地球引力、月球引力、太阳引力等联合作用下月地轨迹优化修正问题，为探月轨道详细设计提供了参考。周亮等[4]基于双体模型详细研究了探月直接返回和间接返回轨迹的性质，仿真分析了各设计参数对月地返回轨道的影响，方法简单直观，易于分析搜索目标轨道。郑爱武等[5]基于Lambert 算法设计初始转移轨道，并结合精确的轨道动力学模型，利用循环搜索算法得到满足各约束条件的转移轨道。

月球探测器返回制导技术也得到了广泛关注。Z.R.Putnam 等[6]深入研究了跳跃式再入问题，并将数值校正预测制导律与传统阿波罗再入制导律进行了对比分析，展示了预测校正制导的优越性。该文献研究了不同再入轨迹倾角及纵向航程下最大横程能力，这对初始指向角设计具有参考意义。Christopher W.Brunner[7]等详细研究了数值再入预测校正制导问题，并基于提前预置偏差量减小制导偏差，得到了较好的效果。

虽然大气层外轨道设计及大气层内再入制导设计分别得到较为充分的研究，但是大气层内外联合设计优化问题并未得到充分关注。部分学者研究了大气层内外轨迹的衔接问题，沈红新等[8,9]分析了再入角和再入经纬度及再入航程随轨道参数的变化关系，设计了着陆点及再入点位置分析方法；赵玉晖等[10]详细研究了地月相对位置和地月转移轨道过渡时间对再入角的影响，对返回窗口的选择具有借鉴意义。但是，由于飞船升阻比较小，横程调节能力差，需要保证再入速度倾角在设计范围内的同时，具有比较准确的方位角，且再入过程中，过载约束是最严苛的约束之一，且在线调整能力弱。本文将基于双二体模型，通过粒子群优化算法，优化返回轨道参数，使得飞行器进入再入点后基于预测校正制导律的再入过程最大过载最小。

1 大气层内外运动特性建模

探月飞船返回过程中，通常需要沿近月停泊轨道加速，出月球影响球，进入月地转移轨道地心段，并以接近第二宇宙速度高速再入。由于再入速度大，通常在首次再入后，飞行器下降到一定高度时，会再次跃起甚至跳出大气层，随后再次下降，即跳跃式再入。探月返回基本过程示意如图1 所示。

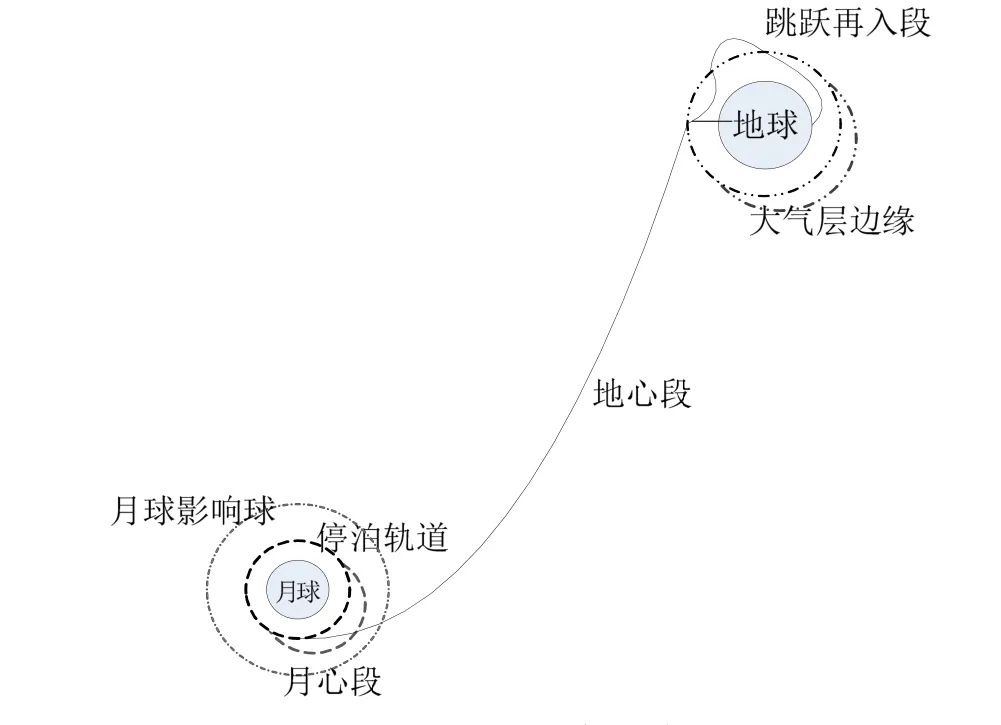
图1 返回过程示意Fig.1 Diagram of Return Process

1.1 轨道建模[4]

假设飞行器自圆形月球停泊轨道返回。选择月球留驻轨道高度hL，轨道倾角iL，出月球影响球点和月心的连线与地月连线夹角δ，出口点月面纬度φL，出月球影响球点月心真近点角fCL，加速点航迹角βAL设计转移轨道。不考虑摄动因素影响，在月球影响球内（半径ρ=66 200km），假设飞行器仅受月球引力作用，出月球影响球后则仅受地球引力作用。加速点即转移轨道月心段近地点，因而可以通过轨道方程求解出月心段偏心率eL和半通径pL。通常这段轨迹为双曲线类型。进而可得出近焦点坐标系下加速点加速后的速度、月球影响球出口点的位置、速度如下：

进而计算月心段纬度幅角、升交点径度和近心点幅角，方法如下：

将出口点转换到月心白道坐标系，即：

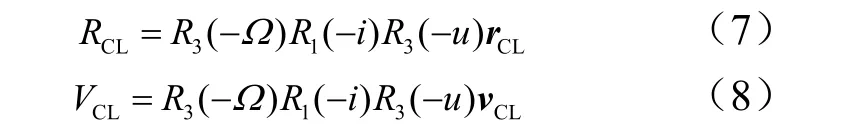
在某一时刻，由JPL星历可计算得到月心白道坐标系下月球距离地球位置和速度REL,VEL。可得在地心白道坐标下，飞行器在月球影响球出口点相对于地心的位置、速度为

转换到地心惯性坐标系，即：

进而得到地心段转移轨道六根数，具体计算方法可参考文献[11]，六根数分别记为：轨道半长轴aE、偏心率eE、轨道倾角iE、近心点角距ωE、升交点精度ΩE、真近点角fCE。考虑直接再入情况，假设再入时刻地心距为rZE，对应的真近点角为fZE，则可计算得到出月球影响球点和再入点对应的地心偏近角ECE、EZE，进而可计算地心段转移轨道飞行时间为

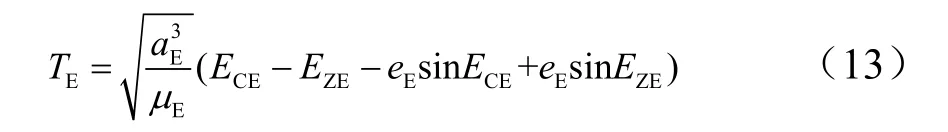
1.2 再入点特征计算

再入点状态主要有再入高度r、再入点经度λ、再入点纬度φ、再入速度V、航迹倾角γ、航迹方向角ψ。逆行轨道90°＜iE≤180°再入会使再入速度较顺行轨道大，对再入过程不利，因此这里仅考虑采用顺行轨道再入。再入高度通常直接给定，距离海平面120 km开始再入。再入速度计算如下：

可见若使再入速度较小，可通过减小轨道半长轴实现，但是由于aE≫r，该数值总是在第二宇宙速度附近。再入地理经纬度计算如下：

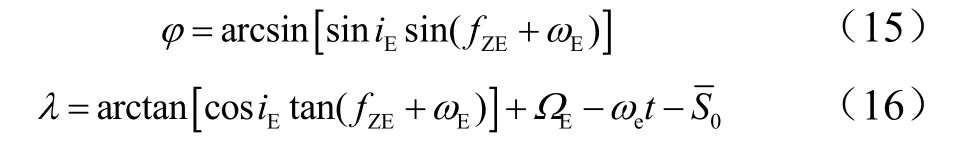
式中ωe为地球自转角速度；为t=0时的格林尼治平恒星时，具体计算方法参考文献[11]。对于航迹倾角和航迹方向角，计算如下：

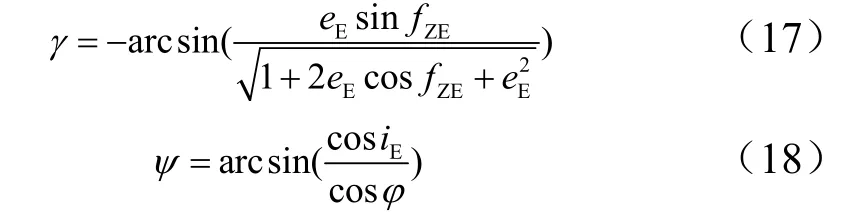
至此，可通过轨道再入点获得全部再入点初始参数。

1.3 再入制导算法[7]

飞行器按照配平攻角再入飞行，通过倾侧角偏转幅值指令调整纵程，通过倾侧角反转调整横程。为此，引入待飞航程，变化率如下：

纵向制导即在每个制导周期内，调整倾侧角σ，使得：

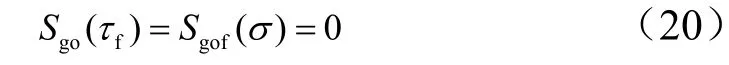
在每制导周期内通过牛顿割线法迭代求解倾侧角幅值指令：

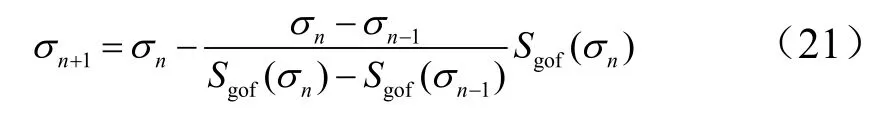
横向制导采用横程边界控制倾侧角符号，从而消除横向偏差。

1.4 大气层内待飞航程

当轨道高度低于120 km 时，飞行器进入再入飞行阶段。本节将主要获取再入阶段待飞航程及经度航程。假设近地点和返回轨道与赤道交点扫过的角度为ϑ1，再入点至近地点扫过角度为，返回轨道与赤道交点至再入点扫过角度为ϑ2。假设近地点纬度、经度、再入点纬度、经度分别为φp,λp,φf,λf，根据球面三角性质，可得：

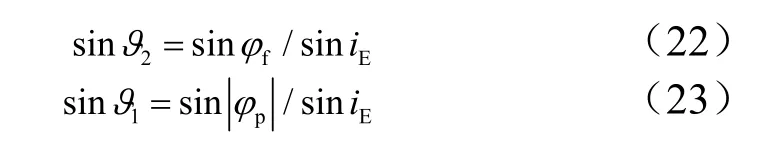
可计算出返回轨道近地点至着陆点待飞角航程：

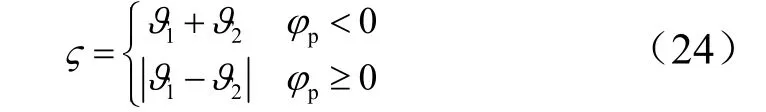
进而可以得到再入点至着陆点待飞航程：

同样，假设ψ1,ψ2分别表示再入点和着陆点在赤道上的投影点至轨道与赤道交点的角度，可得到待飞经度航程计算如下：

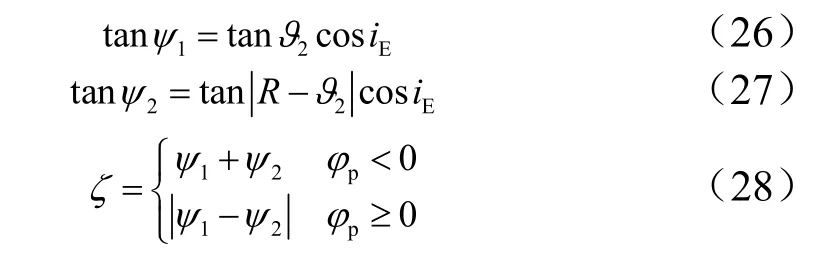
若再入点经纬度为λ,φ，落点经纬度为λf,φf。则可以计算再入点至落点指向角如下：

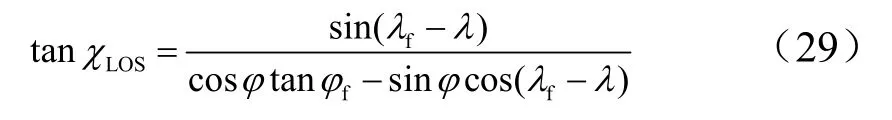
2 大气层内外联合优化算法

再入参数受轨道参数影响巨大，而轨道参数又由转移轨道月心段设计所采用的直观六参数决定。对于中高升阻比飞行器，再入过程中可直接通过对倾侧角指令的调整减弱最大过载[12]，但对于低升阻比飞行器，类似的操作可能大大降低制导精度。本节将利用粒子群算法优化选择设计参数，使得基于预测校正制导的再入过程最大过载最小，同时再入航迹倾角需要满足再入走廊要求，航迹方向角满足指向要求。

待设计参数为第2.2 节所设定的直观六参数。为保证所需加速能量小，通常在月球留驻轨道沿着速度方向加速，即加速点航迹角βAL= 90°。月球留驻轨道可事先设计给定，对返回轨道特性影响较小，因此月球留驻轨道高度hL，轨道倾角iL均可直接给定。对转移轨道特性影响较大的参数主要是出月球影响球点和月心的连线与地月连线夹角δ，出口点月面纬度φL，出月球影响球点月心真近点角fCL3 个参数。因此本节通过δ,φL,fCL的优化选择，使得再入点满足再入走廊约束及指向要求，且再入过程中最大过载最小。记：

为保证飞行器能够再入，需要轨道近地点低于一定的高度，这里要求近地点高度低于100 km，即：

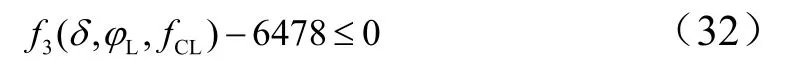
以上3 个约束需要加入到轨迹规划中。再入过程中，低升阻比飞行器过载可简单计算为

再入过程中最大过载为nmax，参数优化问题可表达为

ε1,ε2分别是由满足再入需求的速度倾角范围及侧向制导修正初始指向角偏差的能力所确定的2 个正数。

该问题通过解析优化算法求解容易陷入局部最优，故本文利用粒子群算法[13]进行优化，在一个m维空间下，由N个粒子组成粒子群。第i个粒子及其速度记为

第i个粒子个体极值及整个种群迄今为止搜索到的全局极值分别记为

在找到2 个最优值时，粒子群更新自己位置速度算法如下：

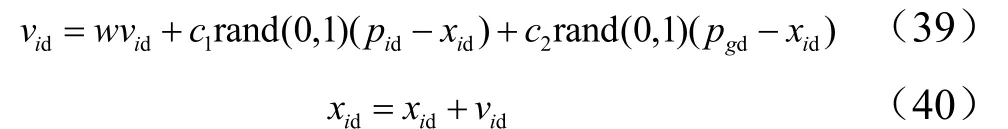
式中w为惯性因子；c1,c2为2 个学习因子，可以通过经验进行选择。

为实现准确的再入制导，需要对置入时刻进行调整，以满足经度匹配。置入时刻调整方法：选定返回时刻t1，计算再入点经度λ1；计算新置入时刻。

经过优化过程（见图2），可以得到满足使再入过程中最大过载最小的参数设计。

3 仿真分析

仿真过程中基本假设条件如下：

a）月球影响球半径取为66 200 km，飞行器加速后，在月心段以双曲线轨道飞出月球影响球；

b）地心段以大椭圆轨道飞向近地点，不考虑双曲线及抛物线情形；

c）不考虑摄动因素及导航偏差的影响；

d）再入初始高度为120 km，再入点初始理想航迹倾角取为-5.5～6.5°；再入初始方向角偏差假设不超过5.73°；

e）月球相对地球轨道参数由JPL 的DE405 星历计算得到。

飞行器模型参考文献[7]，质量8283 kg，参考面积19.684 m2以配平攻角飞行，升阻比为0.289，其中升力系数为0.3892，阻力系数为1.3479，不考虑再入过程中升阻力系数变化。月球停泊轨道高度hL=200 km，轨道倾角iL=40°，加速点航迹角βAL通常取90°最终落点选择为东经112°，北纬42°区域。

粒子群优化过程中，粒子数选择300 个，惯性系数选择为w=0.7，两个学习因子分别取为c1=1.4，c2=1最大迭代次数选择为15 次。3 个参数迭代区间设置为，经过迭代，可得到最优取值（见表1）、月心段及地心段轨道设计结果（见表2）。

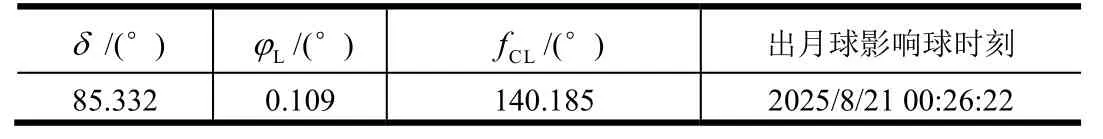
表1 迭代结果Tab.1 Iteration Results

表2 轨道设计结果Tab.2 Trajectory Design Results

再入制导采用第2.3 节所示数值预测校正再入制导算法，经过粒子群算法迭代得到的最大过载最小再入运动基本参数（见表3）。通过表3 可见，再入航迹倾角满足再入走廊的要求，通过式（29）计算的理想航迹偏角为48.543°，与实际航迹偏角误差在允许范围内。再入过程中基本参数变化如图3～6 所示。图3表示再入过程中速度及高度变化曲线，图4 表征再入过程中的制导指令，图5 表示再入过程中过载变化曲线。图6 表示地心轨道段及再入段星下点变化曲线。

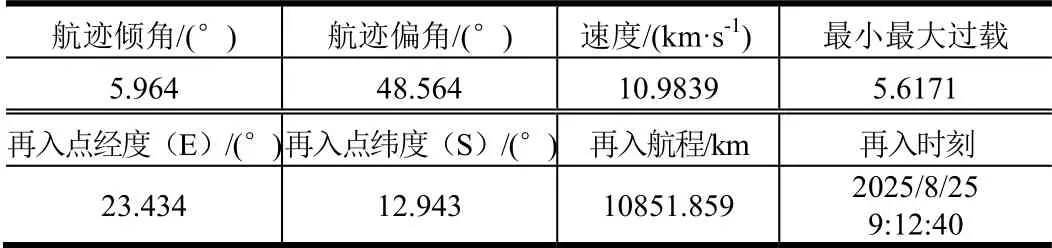
表3 再入运动参数Tab.3 Reentry Motion Parameters

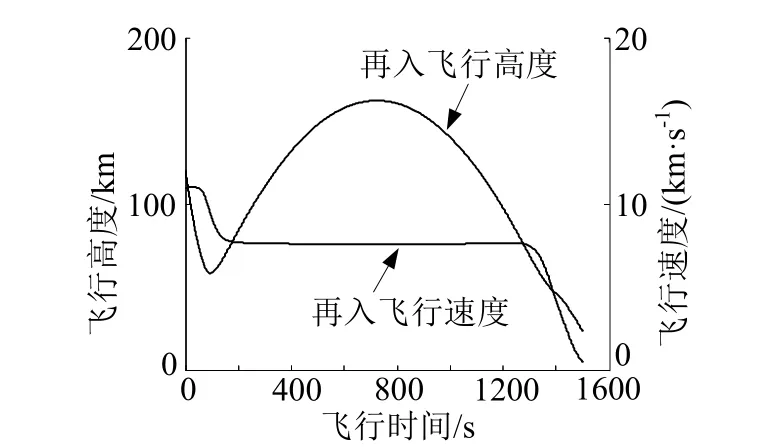
图3 再入过程中飞行速度及高度变化Fig.3 Speed and Altitude Curves During Reentry

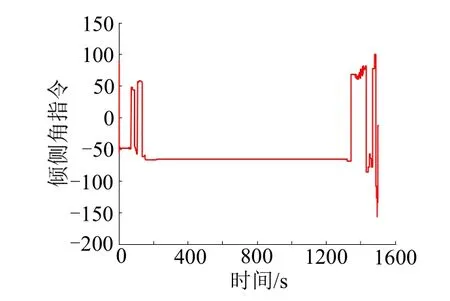
图4 再入制导指令Fig.4 Reentry Guidance Command

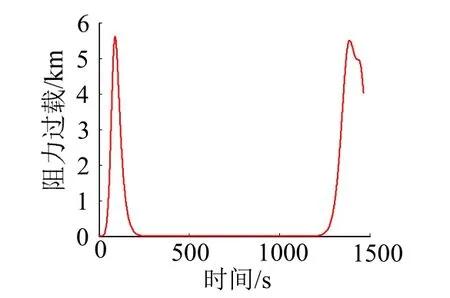
图5 再入过载变化曲线Fig.5 Reentry Overload Curve

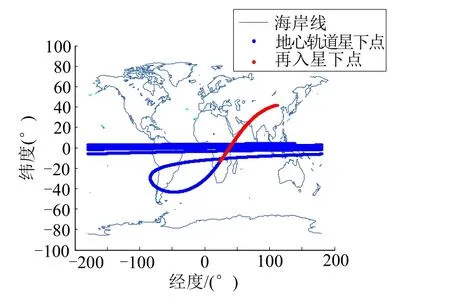
图6 星下点变化曲线Fig.6 Sub-Satellite Curves

通过图3～6 可发现，利用粒子群优化算法得到的设计参数能够将飞行器导引至开伞点。飞行器返回方式为跳跃式再入返回，跃出大气层最高高度约170 km。两次进入大气使得飞行器气动过载具有2 个明显的尖峰，其中最大过载出现在第1 个尖峰处，出现时刻大约对应于再入轨迹再次拉起的时刻。进入再入点后由于跃出阶段不具备横向调整能力且受地球自转影响，会导致一定的固有制导偏差，再入航程较远时知道偏差甚至可达到10 km 级，可通过瞄准虚拟目标点等方式进行补偿，以提高制导精度。

4 结 论

本文主要研究了探月飞行器直接返回大气层内外轨迹联合设计问题。通过粒子群优化算法，得到月球影响球点与月心连线与地月连线夹角、出口点月面纬度及月心真近点角，实现再入最大过载最小。并通过对置入时间的选择，实现对再入点经度的匹配。通过优化设计，能够实现再入点满足再入走廊要求，且速度指向与期望的指向方向偏差能够满足横程要求，最终实现将再入最大过载降低至5.6171g。本文轨道设计结果可作为精确轨迹设计的初值，进一步考虑摄动力，从而使结果更符合实际飞行状态。