船用某型空压机结构辐射噪声特性计算分析

薛厚强，张冠军，胡龙飞，郑立平

（1.武汉理工大学高性能船舶技术教育部重点实验室，武汉430063；2.武汉理工大学能源与动力工程学院，武汉430063；3.中国人民解放军第四八一二工厂，安徽安庆246001）

往复式空压机是一种通过对气体做功以提高气体压力的通用机械，在船上主要用于主动力装置的启动与换向，同时也为其它需要高压气体的设备提供气源。往复式机械通常会产生较大的振动噪声，降低舰船隐身性能，且影响船员工作环境。因此，开展船用空压机结构声学特性的研究，寻求设备的低噪声设计方法，具有重要的理论意义和工程应用价值。

半个多世纪以来，大部分研究是先通过试验进行主要声源定位，然后针对简单零部件进行结构优化。目前数值模拟技术在不断完善，用有限元/边界元联合方法，通过取长补短求解声场问题，可起到相得益彰的效果[1–4]。将有限元与边界元法相结合成为目前最常用的声学数值计算方法，可用于求解具有任意复杂形状表面的结构振动与声辐射问题。但目前多数研究主要针对小型空压机结构[5–8]，而对具有复杂结构空压机的结构振动与噪声研究较少，尤其对于紧凑型船用大型空压机，由于模型和载荷边界条件较为复杂，往往难以得到较为准确的结果。从噪声控制角度出发，研制低噪声船用空压机产品时，应将声学性能计算分析纳入产品设计阶段予以考虑。本文以最新研制的船用大型往复式四级压缩空压机为研究对象，建立其声学特性分析模型，开展基于数值仿真计算的空压机结构辐射噪声特性研究，旨在为同类型空压机声学特性优化提供参考。

1 结构振动声辐射数值计算理论

由弹性力学基础理论可导出多自由度系统结构振动方程[9–10]：

式中：[M]为系统质量矩阵；[C]为系统阻尼矩阵；[K]为系统刚度矩阵；{f(t) }为节点等效动载荷列阵；{δ}为节点位移列阵为节点速度列阵为节点加速度列阵。

求解式（1）即可得到空压机结构振动时的动位移、速度、加速度等变化规律，本文将采用直接积分法进行求解。

由于所计算的空压机表面辐射噪声属于外声场，考虑用直接边界元法进行求解计算。封闭结构振动的声场计算问题如图1所示。由于在边界积分方程中，内部问题中的法向与外部问题的法向不一致，使得求解过程中容易产生误解，这里将内部问题与外部问题的法向统一取为指向结构的外部，其统一形式可以描述为[11]：

图1 结构声辐射示意图

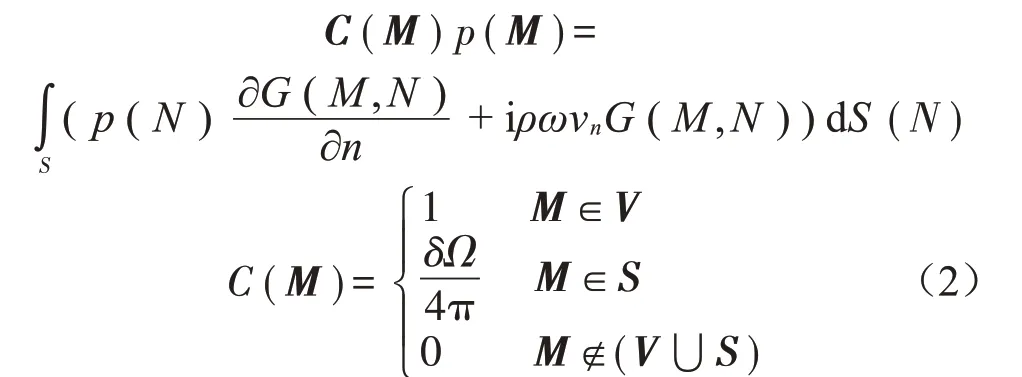
式中：i2=-1；ρ是流体介质的密度；δΩ是点M在结构表面S上时的表面角；p(M)为场点M上的声压；p(N)为结构表面点N上的声压；vn为结构表面上点N的法向速度；G(M,N)为自由空间格林函数，即Helmholtz方程的基本解。

在使用声学Helmholtz 边界积分方程计算空压机的声辐射时，不可能通过解析法得到声场的精确解，需要通过离散边界来求近似解，从而得到声场中任意一点的声压和声速。

2 空压机动力学响应计算及试验验证

2.1 空压机动力学响应分析模型

本文以某船用大型往复式空压机为研究对象分析其声学特性，该型空压机为四级压缩空压机，每级气缸均采用单作用式活塞，通过带有管路消声器的吸气过滤器吸入空气进行压缩，在四级出口达到额定排气压力，然后通过管路将其输送到气瓶。

参照空压机的尺寸利用三维建模软件Solidworks 进行实体建模。在满足分析精度要求条件下，对结构进行适当简化，在建模时对部分结构简化条件如下：

（1）由于研究目标是空压机机体的声辐射，故将与机体相连的电机等部件忽略，仅保留机体本身。

（2）忽略较小螺栓孔与螺钉孔，在网格划分时，可设置约束将各部件连接，若不忽略不仅会增加计算量，还可能在螺栓与螺栓孔处发生网格畸变。

（3）为尽量保证网格质量，删除机体上局部凸台，简化了一些不必要的圆角，将其以直角代替，将某些细小部件直接进行整合，规划在同一个轮廓内。

（4）忽略内部的冷却器等结构，保留机体中所关心的局部结构，以便后续载荷的施加。

由于空压机的结构复杂，若使用六面体网格对其进行划分，会耗费难以预测的时间，且容易造成局部网格质量过低。本文采用四面体单元对简化后的各零部件几何模型时进行网格划分。初步设定不同的单元尺寸，进行自由模态分析，验证有限元网格的收敛性且满足每个波长内有6个单元的条件。

在确定单元尺寸后，对各零部件进行有限元装配。该空压机多数零部件通过螺栓连接条件实现装配，目前对于连接结构的有限元模型处理方式主要有直接连接、局部结点耦合法、采用有限单元模拟及基于实验测定的线性及非线性模型。相关文献表明[12–13]：采用方法2和3对螺栓连接进行简化可以较好反映组合结构的动力学特性，虽然方法2和3忽略了结合面处的阻尼效应。方法4只有在大量实验数据基础上才能实现，本文研究条件不具备。

基于以上分析，采用上述方法3 将各零部件的有限元模型进行连接得到空压机整机有限元模型如图2所示。

图2 空压机有限元模型示意图

2.2 空压机动力学响应分析的边界条件

采用FEM/BEM方法进行空压机辐射噪声特性分析的一般流程是激励源分析-振动响应计算-声学特性计算，正确求解结构振动响应是声学特性研究的前提。在进行空压机振动响应计算时，所涉及到的边界条件为位移边界条件及力边界条件。在实际工作中空压机曲轴箱是固定在地基上的，考虑到地基体积及刚度非常大，可以认为空压机工作时地基的位移为零，所以在施加机体位移约束时对机体底端3个位移自由度采用固定约束。

空压机所受激励载荷很多，但对结构辐射噪声影响最大的载荷还是缸内气体压力、活塞侧推力以及轴承载荷。本文所需的激励载荷通过对空压机在额定工况下进行多体动力学计算得到。实际运行中，空压机曲轴作为主要的运动零部件，其弹性变形和弹性振动对空压机连杆、轴承等零部件的受力情况有较大影响，同时影响着整机的运行。因此，结合有限元方法、多体动力学方法，以空压机转速及气体压力为边界条件，进行空压机运动机构的刚柔耦合（曲轴为柔性体）动力计算，得到轴承载荷、活塞侧推力、气体力。将计算得到的轴承载荷施加于两端轴承座，将活塞侧推力等效施加于缸套与气缸体上下装配的两表面，将气体力施加于缸盖底部。

通过瑞利矩阵来确定系统的阻尼矩阵，如式（3）所示：

式中：α、β为实常数，叫瑞利阻尼系数，可由式(4)确定：

式中：ξ1、ξ2为前2 阶自由模态振型下的阻尼比；ω1、ω2为前2阶自由模态固有圆频率。

进行空压机自由模态分析，得到其前2 阶非刚体模态固有频率分别为77.654 Hz、80.445 Hz，进而可求出前2阶固有圆频率。前两阶模态阻尼比可以按经验取0.02～0.05，这里取0.03，求得瑞利阻尼系数α=14.09，β=6.04×10-5。

2.3 空压机动力学响应分析及试验验证

在进行空压机振动响应分析前，首先对其进行有限元模态分析，以掌握结构的动态特性。采用Lanczos法对空压机组合结构进行有限元模态分析，限于篇幅关系，只给出部分结果，空压机约束模态的固有频率见表1。

表1 空压机组合结构固有频率/Hz

通过各阶固有频率值可以看出，空压机的模态固有频率较为密集，且集中于中低频范围内。因空压机模态比较密集，在后续振动响应计算时也不宜采用模态叠加法进行求解，所以本文将采用Full 法（完全法）进行空压机振动响应分析。

由于主要关心空压机在1 000 Hz内的辐射噪声特性，故在振动响应计算时设定求解最高频率为1 000 Hz。求解得到空压机在额定工况下的结构振动响应。限于篇幅关系，只给出了部分计算结果，如图3、图4所示。

图3 空压机机脚处振动加速度级频谱

图4 空压机3级缸盖处振动加速度级频谱

由上述计算结果可以看出：空压机各节点的振动响应频谱规律相似，其振动主要集中在中低频范围内，在170 Hz、345 Hz、515 Hz、665 Hz、840 Hz 等频率处出现明显的峰值，其中170 Hz、345 Hz、515 Hz、665 Hz、840 Hz分别约为空压机在额定转速下的倍频，说明这些频率下的峰值主要由空压机内部激励引起，与旋转机械的振动规律相吻合。由模态分析结果可知，170 Hz与345 Hz基本与空压机的固有频率相重合，说明在这些频率处空压机被激起共振，从而所激起的能量较大。总体上，空压机上方气缸体振动较为剧烈，曲轴箱振动最小，这主要是因为空压机的机脚处施加了固定位移约束，限制了其3 个位移方向的自由度，所以曲轴箱的振动加速度级整体较小。空压机气缸体振动较大，其原因之一为空压机上方气缸体部分受力较大且复杂；另外，从空压机结构来看，这主要是因为其上方支撑方式较弱，气缸体结构的整体刚度较为薄弱，容易被空压机运行过程中产生的力所激励，从而被激起较大的能量。

为验证空压机振动响应计算方法的正确性，提高计算结果精度，对空压机在额定工况下的振动响应进行测试。

振动测试系统包括加速度传感器、LMS SCADAS III 采集前端及测试软件Test. Lab。加速度传感器采用4535-B-001 振动传感器，其灵敏度为100 mv/g；频率范围为0.3 Hz～10 kHz，工作范围为-60℃～125℃。LMS SCADAS III具有16个麦克风通道，16个智能振动通道及两个转速跟踪通道，每通道最高采集频率为204.8 kHz，本文采样频率设定为25 600 Hz。依据全国船舶专业标准GJB763.4－1989《舰船噪声限值和测量方法舰船设备结构振动加速度测量》和GJB4058－2000《舰船设备噪声、振动测量方法》在空压机上布置测点。

空压机的1级缸盖附近振动加速度级计算数据与试验数据对比如图5所示。

由图5可看出振动加速度级的计算值与试验值随频率变化趋势大体相似，部分频率处的振动幅值相近。计算结果基本能够反映空压机运行过程中的主要振动特性，可校验计算方法的合理性，同时也佐证了所建有限元动力学模型的合理性，为下文声辐射的计算提供了边界条件。

图5 空压机1级缸盖处振动计算与测试的频谱对比

3 空压机结构辐射噪声计算分析

3.1 空压机结构声学响应分析

声学边界元模型的精度不受模型网格尺寸影响，主要取决于网格中的最小尺寸，当声学网格中最大单元尺寸小于最短波长的1/6时，可得到较高的精度。本文分析最高频率为1 000 Hz，考虑到求解资源和结果的准确性，选取模型单元尺寸为35 mm，对整机的表面进行网格划分，根据GJB4058－2000，场点定义为与声源基准体中心相距1 m 的长方体，模型底部施加对称平面模拟地面，此对称平面为刚性平面。所建空压机声学分析模型如图6所示。

图6 空压机结构声学分析模型

将振动响应计算结果导入LMS Virtual.Lab中，并利用四节点插值算法映射至声学边界元模型相应的节点上作为边界条件，设置求解频率范围为20 Hz～1 000 Hz，求解频率间隔为5 Hz，进行空压机辐射噪声计算。

图7 给出了不同频率下由FEM/BEM 方法计算所得空压机空间声场的声压分布云图。

图7 不同频率下的声压云图

由图7 空压机空间场点声压分布云图可知：整体上，空压机底面、两端轴承侧和前后侧面辐射声场中具有较高声压级；另外，辐射声场具有较为明显的指向性，低频时声压级瓣状分布较为明显，随着频率的增加，不同声压值的点状区域面积逐渐变小，整个声场分布趋于均匀。

声场中声压云图主要反映声辐射的空间分布情况，为了解声场中噪声的频率分布情况，需进行声功率频谱分析，以更精确确定空压机辐射声场中突出的频率成分，从声学响应的角度确定声场的主要影响频率。图8 至图9 所示为空压机结构辐射噪声声功率级及声辐射效率的频谱。

图8 空压机辐射声功率级频谱

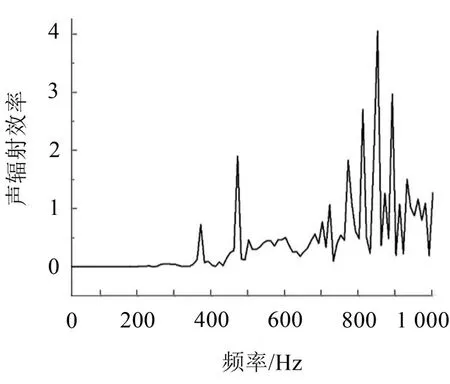
图9 空压机声辐射效率

从图8 至图9 所示空压机结构辐射噪声声功率级及声辐射效率变化规律可以看出：空压机辐射噪声水平在360 Hz 以及770 Hz～840 Hz 频率附近较高；随着频率的增高，空压机声辐射效率基本上呈现增高的趋势。由空压机结构模态及振动响应分析结果可知：345 Hz 附近频率与空压机的模态固有频率相重合，空压机因此而被激起共振，其结构振动较为强烈，可能会导致在该频率附近产生的较大辐射噪声（还与声辐射效率有关），但空压机在345 Hz频率处的声辐射效率（0.05）远小于空压机在360 Hz处的声辐射效率（0.13），所以即使空压机在360 Hz 频率处的振动响应比345 Hz频率处的振动响应稍小，但在360 Hz频率也会产生较大的辐射噪声。而在770 Hz、810 Hz 以及840 Hz 频率附近，主要由于空压机的声辐射效率较高，该频率下空压机振动-声辐射系统中辐射噪声的能力较强，因此产生的辐射噪声也较大。

3.2 空压机结构面板声学分析

为确定空压机结构的主要辐射噪声源，以便有针对性地改善其结构辐射噪声，应求出各板件的声学贡献量，确定对噪声峰值贡献突出的板件，以对其进行结构优化改进，降低空压机结构辐射噪声水平。根据空压机自身结构组成特点，本文在空压机边界元模型中划分62个不同的面板区域。

面板声压贡献量的研究主要集中在面板对声场中某个或某几个场点声压贡献量的分析，但所选取的场点并不能完全体现整个声场的辐射噪声特性，难以满足空压机的降噪要求。声功率可以更全面反映结构的噪声辐射贡献量，因此本文从面板声功率级贡献量的角度，利用ATV 法[14]分析空压机结构噪声的主要辐射部位，部分计算结果如图10 至图11所示。

图10 空压机面板声功率贡献

图11 空压机面板声功率贡献

由360 Hz 下面板的声功率贡献图可知，面板22、39、34、35、45 的声功率贡献量较大，面板幅值由大到小排列为22、39、45、34、35，即面板声学贡献量由大到小为1-B级油水分离器外壳、1-C级气缸体上表面、2 级气缸体上表面、1-B 级气缸体端面、1-B 级气缸体底面。由770 Hz 下面板的声功率贡献图可知，面板1、4、6、30、48的声功率贡献量较大，面板幅值由大到小排列为48、30、6、4、1，即面板声学贡献量由大到小为2级气缸体端面、1.1级气缸体端面、曲轴箱右下方侧面、曲轴箱左下方侧面、曲轴箱底面。

由810 Hz 下面板的声功率贡献图可知，面板30、42、47、48、53 的声功率贡献量较大，面板幅值由大到小排列为42、53、30、47、48，即面板声学贡献量由大到小为1-C级气缸体端面、3级气缸体端面、1-A级气缸体端面、2 级气缸体端面、2 级气缸体底面。由840 Hz下面板的声功率级贡献图可以观察到，面板39、41、42、47、53的声功率贡献量较大，面板幅值由大到小排列为41、39、42、53、47，即面板声学贡献量由大到小为1-C级气缸体底面、1-C级气缸体上表面、1-C 级气缸体端面、3 级气缸体端面、2 级气缸体底面。

为了更直观地表征上述面板声功率级贡献分析结果，将其整理排序如表2所示。

表2 不同频率下面板声功率级贡献量/dB

从表2中不同频率下面板声功率级贡献量可以看出，面板22、30、39、41、42、48、53（1-B级油水分离器外壳、1-A级气缸体端面、1-C级气缸体上表面、1-C 级气缸体底面、1-C 级气缸体端面、2 级气缸体端面、3级气缸体端面）对空压机辐射噪声水平影响比较大。空压机上方结构的支撑较弱，同时气缸体端面及底部结构比较薄弱、刚度小，容易引起振动进而产生较大的辐射噪声。

4 结语

本文基于FEM/BEM方法建立船用空压机振动噪声分析模型并进行计算，揭示了空压机的振动声辐射特性，主要得到如下结论：

（1）采用有限元与边界元相结合的方法，计算分析空压机结构辐射噪声特性，研究表明：空压机结构辐射噪声水平在360 Hz 以及770 Hz～840 Hz 附近较高，与其结构振动特性及声辐射效率有密切关系。

（2）通过空压机空间声场分布分析得出：空压机底面、两端轴承侧和前后侧面辐射声场中具有较高声压级；此外，辐射声场具有较为明显的指向性，低频时声压级瓣状分布较为明显，随着频率的增加，不同声压值的点状区域面积逐渐变小，整个声场分布较为均匀。

（3）基于声学传递向量法分析了空压机面板声学特性，分析结果表明：1-B级油水分离器外壳、1-A级气缸体端面、1-C 级气缸体上表面、1-C 级气缸体底面、1-C 级气缸体端面、2 级气缸体端面、3 级气缸体端面对其辐射噪声水平影响比较大，在进行低噪声设计时应予以重点考虑。