广义位势理论本构模型的加卸载准则探讨

钟志辉，杨光华，张玉成，官大庶，温 勇

(1.广州市宏禹水利水电勘测设计有限公司，广东 广州 511458；2.广东省水利水电科学研究院，广东 广州 510635；3.华南农业大学 水利与土木工程学院，广东 广州 510642；4.中国矿业大学，江苏 徐州 221008；5.广东水利电力职业技术学院，广东 广州 510610；6.仲恺农业工程学院 城乡建设学院，广东 广州 510225)

1 概述

岩土本构理论一般将土的状态分为弹性状态和塑性状态，其中加卸载准则是用于判断土是处于加载还是卸载的状态，不同状态下一般会采用不同的应力应变关系。经典弹塑性理论是通过屈服函数来确定加卸载准则的，但试验表明土的应力应变关系较为复杂，从而导致屈服面的确定或建立也较为复杂。目前岩土的弹塑性模型的屈服面都基于一些假设条件而建立的。然而，土的屈服面是否唯一也无法严格的证明。基于单一屈服面推导出来的加卸载准则存在一定的局限性，因此沈珠江[1-2]、向大润[3]等提出部分屈服加卸载准则。此外，鉴于建立屈服面型加卸载准则的困难，部分学者建议采用应力型加卸载准则和应变型加卸载准则[4-5]。

为了克服经典弹塑性理论假设多、屈服面复杂等缺点，杨光华[6-9]直接从数学原理出发，提出了土体本构模型的广义位势理论。广义位势理论的优点是数学原理清晰，不需要以塑性公设为基础，其建立的本构模型从理论上来讲更为科学和完善。近年来广义位势理论逐渐得到更多学者的研究和应用[10-17]。然而，基于屈服面确立的加卸载准则用于广义位势理论的本构模型，或者采用其他方式建立加卸载准则，仍需更多的研究和探讨。鉴于此，本文从数学角度阐述广义位势理论中加卸载准则的数学本质，为建立合理的加卸载准则提供数学依据，最后提出一种普遍适用于广义位势理论本构模型的分段型加卸载准则。

2 广义位势理论本构模型的加卸载准则

2.1 基于广义位势理论建立土的本构模型[7]

基于广义位势理论建立土的本构模型，只需解决2个基本问题：① 确定土在主应力空间中的应力应变关系，本文又称为状态方程；② 确定(塑性)应变增量的3个势函数。

首先，状态方程一般通过数学方法拟合试验数据得到，根据主应变类型的不同可以分别写成如下2种形式：

εi=fi(σ1,σ2,σ3)

(1a)

(1b)

(2a)

(2b)

然后，根据广义位势理论，塑性应变增量张量可表示为：

(3a)

(3b)

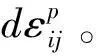
当塑性应变增量用3个势函数表示时，称为多重势面模型；当塑性应变增量用2个势函数表示时，称为二重势面模型；当只用1个势函数表示时，就退化为经典的弹塑性模型。

一般式(3)中3个塑性势函数可以取为σ1,σ2,σ3(或p，q，Lode角θ)。当选用σ1,σ2,σ3作为分段条件，分段条件具有明确的物理意义，而且较为简单实用。

2.2 三维应力空间的分段型加卸载准则

一般状态方程是在主应力空间中确定的，只要能够合理地对状态方程进行分段，那么这个分段型加卸载准则是可行的。

最简单的3个分段条件是σ1,σ2,σ3(或p，q，θ)，因为在三轴试验中，每个状态方程一般是通过改变其中1个主应力、而另外2个主应力保持不变确定的。例如，保持σ2和σ3不变，分别增加或减少σ1，就拟合出2个不同的状态方程。由此可见，1个简单又合理的分段条件可以表示为：

(4)

这是最基本的分段条件，如果要描述更为复杂的状态方程，必须加入更多的分段条件。

2.3 二维应力空间的分段型加卸载准则

(5a)

(5b)

或者表示为：

(6a)

(6b)

式中A、B、C、D为待定参数，通过拟合试验数据得到。可见，最基本的分段条件应该为：

(7)

或者为：

(8)

如果要描述更为复杂的状态方程，也必须加入更多的分段条件。例如沈珠江[2]提出的部分屈服条件也包含式(8)所列的分段条件，但另外增加了一个分段条件η=q/p。

2.4 屈服面型加卸载准则

传统的弹塑性本构模型一般采用屈服面f(σij,H)=0建立加卸载准则，其中H为硬化参数。当应力状态位于屈服面上时，土体处于加载或中性变载状态；当应力状态位于屈服面内时，土体处于卸载状态。

由于屈服面较难确定，因此，一般是采用塑性势面代替的，即所谓的关联流动法则。杨光华[7]指出，状态方程必须满足一定的条件，关联流动法则才成立。如对于式(6b)，只有当B=C，AD=BC时，屈服面才等于塑性势面，此时状态方程可以采用屈服面建立分段条件。然而，上述条件在一般情况下较难满足，即使条件满足，推导屈服面的过程也较为困难。

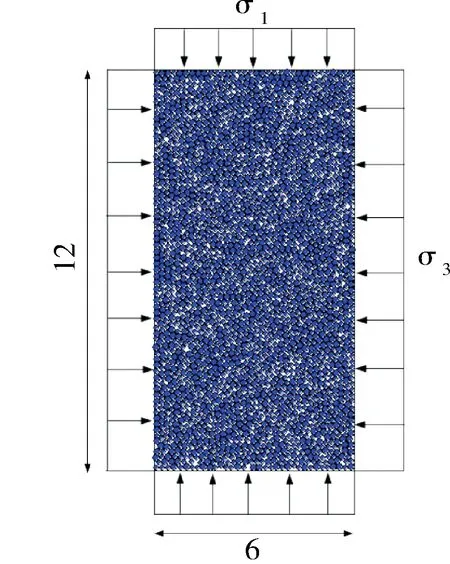
图1 双轴试验的“试样模型”示意(单位：mm)

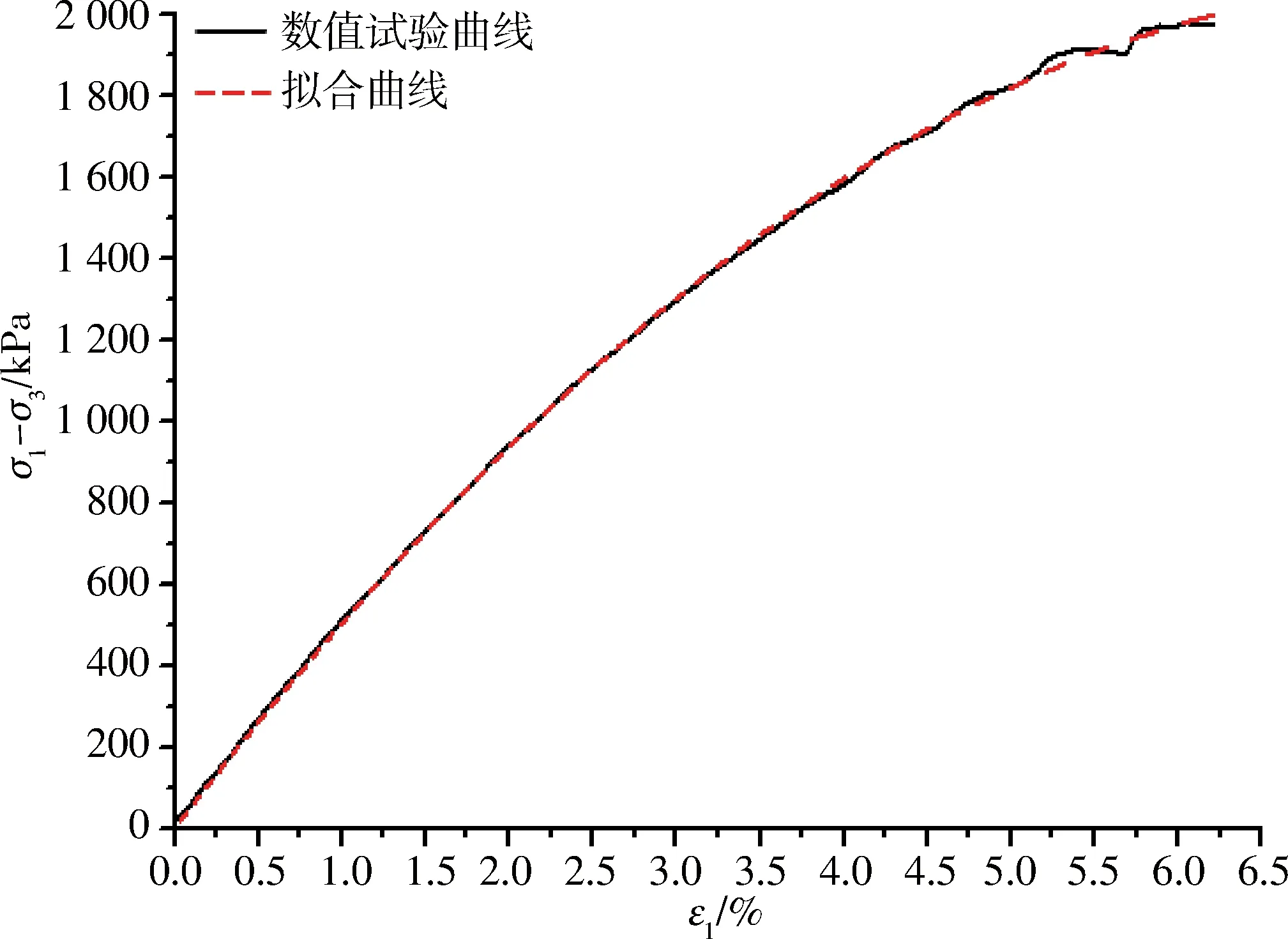
a σ1-σ3与ε1的关系曲线

b σ1-σ3与-ε3的关系曲线

因此，屈服面型加卸载准则作为单一的分段条件，较难全面地反映土体的状态方程的分段情况，用于广义位势理论的本构模型有一定的局限。

3 分段型加卸载准则建立步骤示例

3.1 示例模型介绍

采用平面双轴试验来说明分段型加卸载准则的建立步骤。该双轴试验采用二维颗粒流程序PFC2D模拟，PFC2D通过生成微小的颗粒单元并定义单元的微观参数，从而生成由大量颗粒组成的宏观模型，通过分析宏观模型的受力和变形，就能得到宏观参数。

本示例的试样模型如图1所示，“试样”宽为6.0 mm，高为12.0 mm，设置颗粒的最小半径为0.075 mm，最大半径为0.1 mm，由PFC2D随机生成的2 574个颗粒组成。“试样”的初始围压为1 200 kPa，在初始围压作用下，初始孔隙率达到了0.14。模型四周采用墙体单元包围，四周压力作用在“墙体”上，颗粒单元和墙体单元的计算参数见表1所示。

表1 双轴数值试验的计算参数

本示例采用的状态方程为式(5a)，分段型加卸载准则采用式(7)。

3.2 σ1=σ1max,σ3=σ3max时的状态方程

σ1=σ1max,σ3=σ3max是指σ1、σ3都处于加载条件，其增量形式为dσ1>0，dσ3>0，此时可以通过以下应力路径确定状态方程：① 保持σ3不变，增加σ1，以此确定状态方程的A、C；② 保持σ1不变，增加σ3，以此确定状态方程的B、D。

3.2.1保持σ3不变，增加σ1

当保持σ3不变，增加σ1时，PFC2D得出的应力应变曲线和拟合曲线如图2所示。

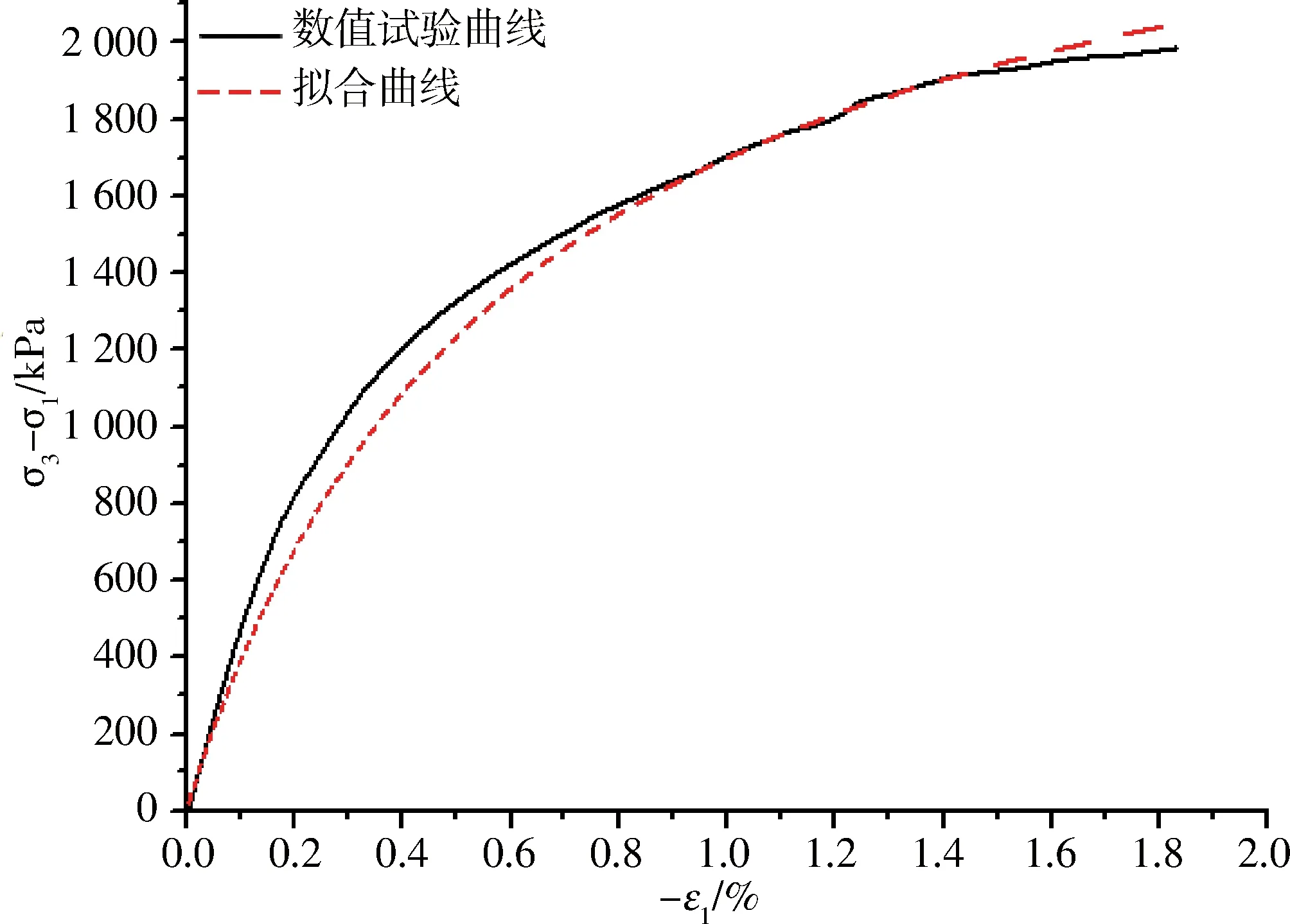
a σ3-σ1与-ε11

b σ3-σ1与ε3的关系曲线

3.2.2保持σ1不变，增加σ3

当保持σ1不变，增加σ3时，PFC2D得出的应力应变曲线和拟合曲线如图3所示。

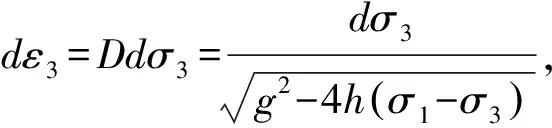
σ1=σ1max,σ3=σ3max时的状态方程可以通过上述2个拟合结果进行叠加，即：

3.3 σ1<σ1max,σ3=σ3max时的状态方程

σ1<σ1max,σ3=σ3max是指σ1处于卸载条件、σ3处于加载条件，其增量形式为dσ1≤0，dσ3≥0，此时可以通过以下两种应力路径的试验结果进行叠加确定状态方程：①保持σ1不变，增加σ3，即dσ1=0，dσ3>0；②保持σ3不变，减少σ1，即dσ1<0，dσ3=0。应力路径①的结果见3.2.2节；按应力路径②进行试验时，PFC2D得出的应力应变曲线如图4所示。

a σ1-σ3与ε1的关系曲线

b σ3-σ1与ε3的关系曲线

与3.2.2节的拟合结果进行叠加，可得σ1<σ1max,σ3=σ3max时的状态方程为：

3.4 σ1=σ1max,σ3<σ3max时的状态方程

σ1=σ1max,σ3<σ3max是指σ1处于加载条件、σ3处于卸载条件，其增量形式为dσ1≥0，dσ3≤0，此时可以通过以下两种应力路径的试验结果进行叠加确定状态方程：① 保持σ3不变，增加σ1，即dσ1>0，dσ3=0；② 保持σ1不变，减少σ3，即dσ1=0，dσ3<0。应力路径①的结果见3.2.1节；按应力路径②进行试验时，PFC2D得出的应力应变曲线如图5所示。

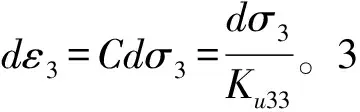
a σ3-σ1与-ε1的关系曲线

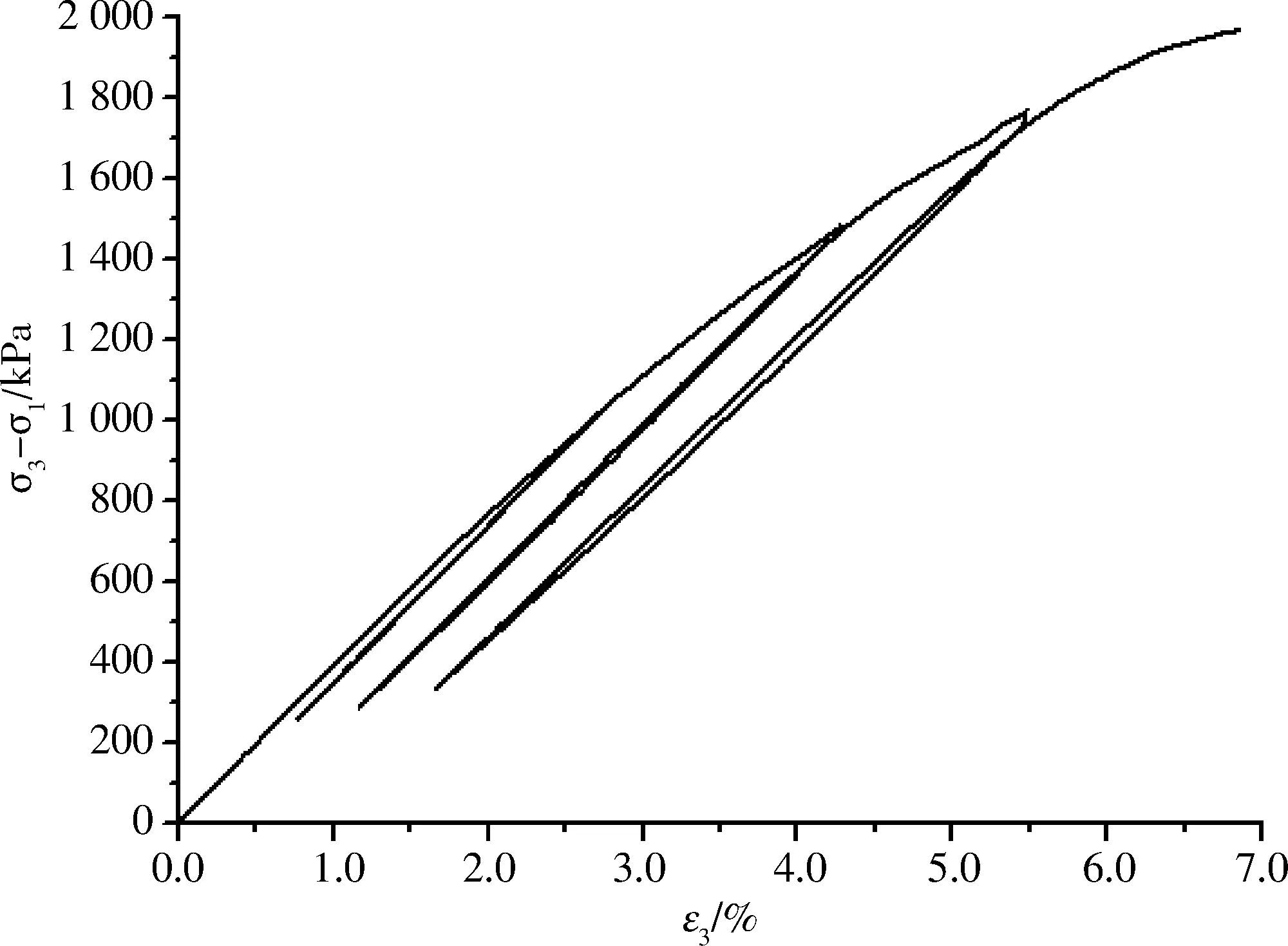
b σ3-σ1与ε3的关系曲线

图6 三轴试验的试样模型示意(单位：mm)

图7 验证试验的应力路径示意

与3.2.1节的拟合结果进行叠加，可得σ1=σ1max,σ3<σ3max时的状态方程为：

3.5 σ1<σ1max,σ3<σ3max时的状态方程

σ1<σ1max,σ3<σ3max是指σ1、σ3都处于卸载条件，此时的状态方程可通过3.3节、3.4节的试验拟合结果进行叠加，即：

综上所述，不同分段条件下的状态方程是不一样的，应采用不同的应力路径确定。对于复杂的本构关系，分段条件应适当增加。

4 分段型加卸载准则应用实例—类剑桥模型

4.1 类剑桥模型简介

广义位势理论中的p-q型二重势面模型[7]，其状态方程按式(6b)表示。2个塑性势函数取为φ1=p，φ2=q，此时式(3b)变为：

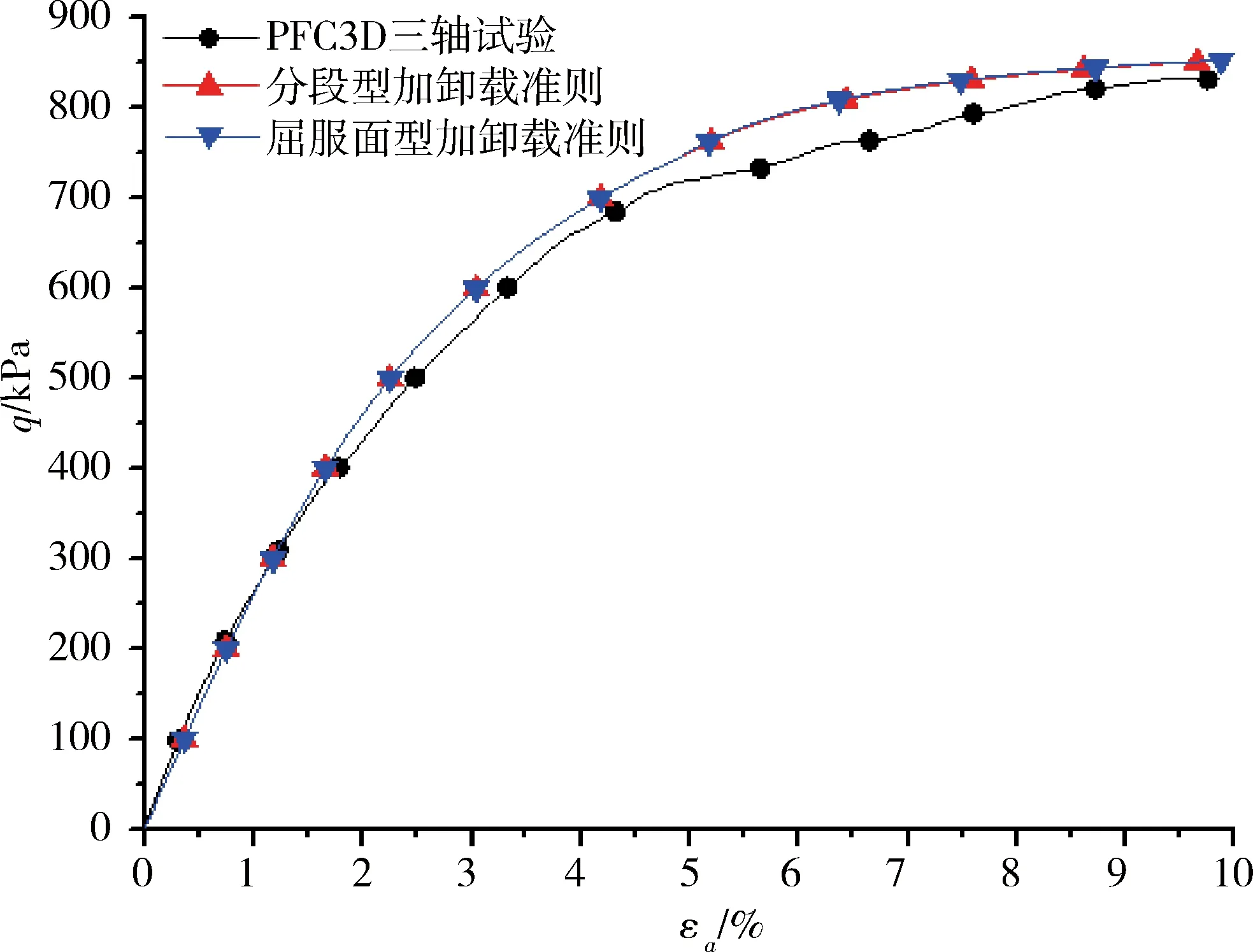
a 轴向应变—偏差应力关系曲线

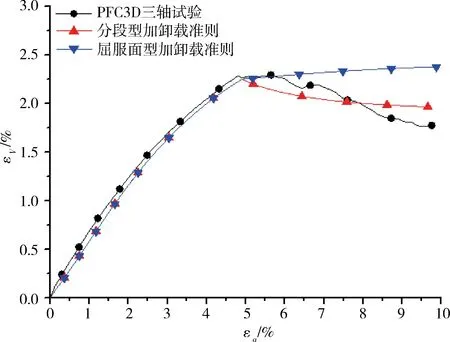
b 轴向应变—体应变关系曲线

a 轴向应变—偏差应力关系曲线

b 轴向应变—体应变关系曲线

a 轴向应变—偏差应力关系曲线

b 轴向应变—体应变关系曲线

(9)

由式(9)可得：

(10)

式(10)代入式(6)得：

(11)

又因为：

(12)

将式(11)和(12)代入式(9)得：

(13)

式(13)即为塑性本构方程，加上弹性应变，即可得数值计算用的弹塑性本构方程。

针对正常固结粘土加载条件下的变形特点，并借鉴剑桥模型，杨光华基于广义位势理论提出了一个类剑桥模型[16]，其状态方程的表达形式为：

(14)

其中：

(15)

(16)

(17)

式中 参数M、λ、κ分别为极限应力比、压缩指数、回弹指数；参数n为拟合参数；e为孔隙比。

4.2 类剑桥模型的屈服面型加卸载准则

传统的加卸载准则一般通过屈服面确定。由于式(14)满足关联流动法则的条件，因此可将塑性势面代替屈服面，从而可以推导出基于屈服面的加卸载准则。根据式(14)，塑性应变增量方向为：

(18)

设屈服轨迹为f(p,q,H)=0，由一致性条件可得：

(19)

根据关联流动法则：

(20)

联立式(18)(19)和(20)解得：

(21)

解微分方程(21)得出屈服函数为：

(22)

式中p0为等向固结压力，可视为该屈服面的硬化参数。

当f<0时，为弹性状态，状态方程为：

(23)

4.3 类剑桥模型的分段型加卸载准则

式(14)是在加载的条件下才成立的，即p=pmax，q=qmax，但此状态方程并不包含部分卸载和完全卸载的情况。根据2.3节的式(8)，本文初步提出类剑桥模型的分段型加卸载准则及对应的状态方程如下：

1)p=pmax，q=qmax时，为式(14)。

2)p

(24)

3)p=pmax，q

(25)

4)p

(26)

应当指出，类剑桥模型隐含着一个剪切破坏条件，即η=M。

4.4 两种加卸载准则的对比分析

验证思路：① 通过三轴试验确定试样的类剑桥模型的参数，本节采用PFC3D构建三轴试验的“试样”，并模拟“试样”的三轴试验；② 采用PFC3D模拟“试样”在不同应力路径的三轴试验，通过对比不同应力路径的试验数据与两种加卸载准则的计算数据，以说明哪种加卸载准则更为合理。

首先，在PFC3D中建立的“试样模型”如图6所示，“试样模型”直径为3.0 mm，高度为6.0 mm，由2 492个球体颗粒组成，颗粒最小半径为0.075 mm，最大半径为0.2 mm。“试样模型”四周采用“墙体”单元包围，外部压力直接作用在“墙体”上。“试样模型”颗粒的计算参数见表2所示。

表2 数值试验的计算参数

采用PFC3D对“试样”进行三轴试验模拟，得出“试样”宏观上的应力应变数据，由应力应变数据计算得出类剑桥模型的参数见表3所示。

表3 类剑桥模型的计算参数

验证类剑桥模型及两种加卸载准则的计算精度，验证的应力路径如图7所示(σa为轴压，σc为围压)，首先各向等压固结到A点(此时围压为1 200 kPa)，然后进行三轴压缩试验(应力路径AB)，最后分别进入3种应力路径：① 路径BC，此时p减少，q增加；② 路径BD，此时p增加，q减少；③ 路径BE，此时p不变，q减少。

分段型加卸载准则和屈服面型加卸载准则的预测结果见图8～10，可见两者得出的εa～q曲线与试验结果的吻合程度较高，而εa～εv曲线的吻合程度相对较低。

总体而言， 分段型加卸载准则的计算结果与数值试验结果较为接近，而屈服面型加卸载准则的预测精度相对较差，由此可见，采用分段型加卸载准则更为合理。

5 结语

本文探讨了基于广义位势理论的本构模型的加卸载准则的数学实质，说明了加卸载准则在本质上是状态方程的分段条件，并提出了分段型加卸载准则。最后，以一个二重势面模型——类剑桥模型为例，论述了其分段型加卸载准则和屈服面型加卸载准则的建立步骤，并比较两个加卸载准则在不同应力路径下的计算结果，结果表明分段型加卸载准则的计算精度相对较高，更加适用于广义位势理论的本构模型。