气-液耦合双作用行波热声制冷系统数值模拟研究

迟佳欣 徐静远 张丽敏 李 萍 罗二仓

(1 中国科学院理化技术研究所低温工程学重点实验室 北京 100190；2 中国科学院大学 北京 100049；3 帝国理工学院化学工程系 英国 SW7 2AZ)

社会的生产离不开能源的利用，传统化石能源的大规模开发，导致环境污染、能源短缺等问题日益严峻。据调查，我国工业能耗高达全国总能耗的70%以上，而其中60%的工业能耗以中低温余热形式流失，造成环境的热污染并大幅降低了系统的能源利用率[1]。因此，能源的高效利用技术成为我国急需解决的重大问题。热声技术是一门新兴的能量转换技术，可以利用可压缩流体往复振荡过程中的热相互作用进行制冷[2-3]、泵热[4-5]或发电[6-7]。系统使用氦气等惰性气体或氮气等环保气体为工质，具有无机械运动部件、寿命长、节能环保等优点。

1991年，R.Radebaugh等[8]首次提出热声驱动脉管制冷机，利用热声发动机驱动脉管制冷机代替了传统的机械压缩机，彻底消除了系统内机械运动部件。1996年，Chen Guobang等[9]提出了国内首台双驻波型热声发动机，工质为氮气时最高可获得1.12的压比，运行频率仅为25 Hz。由于双驻波型热声热机的回热器和谐振管均由驻波声场控制，具有固有的不可逆性而效率较低，2004年，Luo Ercang等[10]首次提出双环路行驻波混合型热驱动室温热声制冷机，系统在压力为3 MPa，制冷温度为250.9 K下，获得了250 W的制冷量，最低制冷温度达到208.6 K，实验结果表明，热驱动热声制冷系统在家用制冷方面具有较大的应用潜力。随后，其团队又在此基础上设计了一台同轴行驻波混合型热驱动室温热声制冷机，在253 K的制冷温度下，将制冷量提升至340 W[11]。但由于热声制冷机入口处于驻波声场，声功存在一定损失，限制了其效率的提升。2010年，K.De Blok[12]提出了四级双行波型热声发动机，当采用氦气为工质时，系统最低起振温度为315 K，该结果表明，环路型热声热机在低品位热能利用领域具有巨大的应用潜力。2017年，Jin Tao等[13]提出了非对称结构的双行波型行波热声发动机,采用二氧化碳为工质时，系统的起振温度为 302 K。2019年，王慧志等[14]提出直连型热驱动室温热声制冷机，在加热温度为573 K，制冷温度为263 K，环境温度为323 K下，整机热效率达到0.44，获得了4.54 kW的制冷量，结果表明该研究在制冷卡车及渔船等方向具有一定的应用前景。双行波环路型热驱动热声制冷机的回热器和谐振管均由行波声场控制，理论和实验均表明其具有更高的热制冷系数和功率密度。但由于传统热声系统中采用气体谐振结构，气体工质的密度较小，使其具有较低的声学惰性，系统效率难以提升且整机系统过于庞大，限制了热声制冷系统的进一步发展。2013年，李东辉等[15]提出了热声驱动气-液双作用行波热声发动机，采用U型气液谐振器代替传统气体谐振管，有效利用了液体谐振器的高质量惯性声感和气体谐振器的高可压缩性声容，在平均压力为1.5 MPa，加热量为1.2 kW时，获得了1.4的压比。2020年，Xu Jingyuan等[16]提出了气液耦合型热声制冷系统，计算结果显示，相比传统气体谐振器，采用气液耦合谐振器的系统频率可从53.3 Hz降至12.3 Hz，压比从1.06增至1.32，从而使系统起振温差从144.1 K降至35.5 K，表明气液耦合型热声制冷系统可以显著提高系统效率及降低系统起振温度，从而有效利用低品位能源，具有广阔的应用前景。

基于此，本文提出一种气-液耦合型双作用行波环路热声制冷系统，采用数值模拟分析了系统的工作特性。对三级气-液耦合双作用行波热声制冷系统的重要参数的沿程分布进行了研究，分析了不同级数下系统的声功、热声转换效率等特性参数，对比了不同单元级数在发动机不同加热温度下，制冷机的制冷量及整机系统的相对卡诺效率变化。

1 系统流程及结构参数

图1所示为本文提出的气-液耦合双作用行波环路热声制冷系统，系统包括三个基本单元，每个基本单元依次包括热声发动机、热声制冷机和U型气液耦合谐振器。热声发动机由室温换热器、回热器、高温换热器组成；热声制冷机由室温换热器、回热器、冷端换热器、热缓冲管组成。其中热声发动机和热声制冷机的连接形式采用直连型，即直接通过热缓冲管相连，取消了传统发动机和制冷机之间的调相器，使系统结构更加紧凑，同时有利于减少声功损失。U型气液耦合谐振器的上方为气体工质，下方为液体工质，中间采用弹性橡胶膜进行气液分离及抑制声直流现象。系统运行时，当回热器轴向温度梯度超过临界值时，自激热声振荡开始，热声发动机产生的声功传递到热声制冷机中产生制冷效应，剩余声功通过U型气液耦合谐振器进行调相。为避免系统运行过程中出现压缩腔和膨胀腔因温度不同造成压力差异，导致弹性膜始终处于拉伸状态、系统效率降低的情况，系统特别增设了气压平衡机构，分别从三台热声发动机的入口处引出一长管段并汇聚于三相平衡阀处，使系统各基本单元间的平均压力保持一致，系统具体结构参数如表1所示。

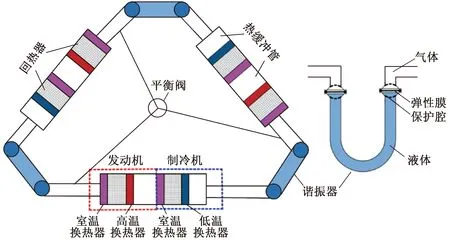
图1 气-液耦合双作用行波环路热声制冷系统Fig.1 Gas-liquid coupled double-acting thermoacoustic refrigeration system

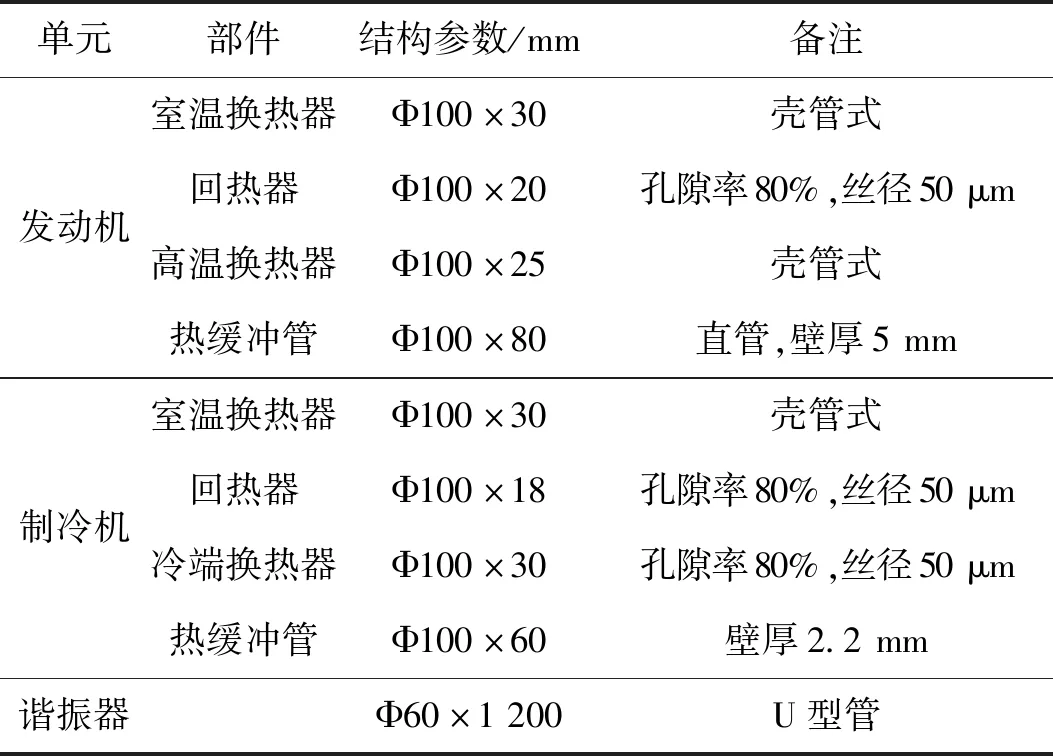
表1 热声核心单元主要结构参数Tab.1 Main geometric dimensions of the components in each subunit

2 系统模拟分析

2.1 计算模型

根据经典热声学理论，本文采用SAGE软件对气-液耦合双作用行波热声制冷系统进行了数值模拟。SAGE软件是由Gedeon Associates提出的一款针对回热式热机的模拟软件，此软件由用户在可视化界面上定义与实际系统相对应的数据块，并给出其对应的进出口参数、边界条件后，依据一维的基本热声学方程进行迭代计算并优化，广泛应用于热声热机、脉管制冷机和自由活塞斯特林系统[17]。

对于气体工质，控制方程如下：

(1)

(2)

(3)

式中：ρ为气体工质的密度，kg/m3；A为流道截面积，m2；t为时间，s；u为速度，m/s；x为声传播方向的位移，m；pl为压力波动幅值，Pa；F为黏性张力项；e为单位质量气体能量，J/kg；q为轴向上瞬时热流密度，W/m2；Qw为轴向上单位长度的热流，W。

对于U型谐振器中的液体，将其视为不可压缩流体，采用SAGE软件中的RECIPROCATOR模块进行模拟，将其看作液体弹簧，通过弹簧常数K和阻尼系数R表征其特性：

(4)

(5)

式中：g为重力加速度，m/s2；D和l分别为液柱的直径及长度，m；ρl、μl、Xl、rt分别为液体的密度(kg/m3)、动力黏度(kg/(m·s))、位移(m)、管半径(m)；E与U型管中的能量损失相关；f为频率，Hz。

在模拟过程中，为了合理评估系统的性能，引入相关变量如下：

对于热声发动机、热声制冷机内声功，定义为：

(6)

式中：Ul为体积流率，m3/s；θp-U为压力波动超前体积流率的相位角，(°)。

对于热声发动机，热声转换效率的定义为：

η=ΔWe/Qh

(7)

式中：ΔWe为热声发动机净产生声功，W；Qh为热声发动机输入热量，W。

对于热声制冷机，系统热制冷系数的定义为：

COP=Qc/Qh

(8)

式中：Qc为热声制冷机的制冷量，W。

由于系统为对称结构，各基本单元的进出口相位差和沿程的参数分布一致，故本文仅模拟了其中一个基本单元，通过调整进出口相位差改变模拟的单元级数。

2.2 模型验证

为确保模型准确性，采用SAGE软件搭建了一个三级环路气液耦合热声发动机模型与实验结果[18]进行验证。系统包括三个基本单元，每个基本单元依次包括热声发动机和U型气液耦合谐振器，热声发动机由室温换热器、回热器、高温换热器和次级室温换热器组成组成。其中，后文计算模型所含部件均可在此系统中得到验证。

图2所示为不同平均压力下系统加热量和运行频率的模拟与李东辉[18]实验结果的对比。系统加热温度为440 K。由图2可知，模拟结果与实验结果较为吻合，误差在25%以内，表明该模型可有效预测类似的实验结果，验证了模型的有效性。

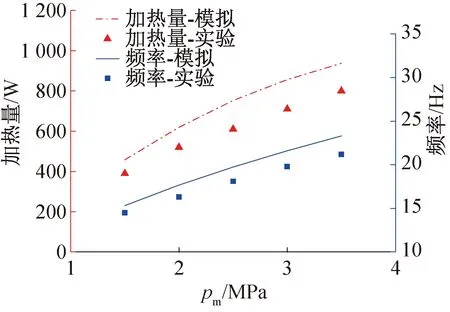
图2 系统加热量和运行频率的模拟与实验结果[18]对比Fig.2 Comparison of simulation and experimental results[18] of heating power and frequency

2.3 系统性能模拟

与传统热声制冷系统相比，气-液耦合双作用行波热声制冷系统采用U型气液谐振器替代了传统的气体谐振管，利用液体的高质量惯性声感和气体的高可压缩性声容形成气液耦合振荡。对于传统的气体谐振管，由于气体工质的密度较低，声感较小，导致系统的工作频率较高、压比较小，不可逆损失较大，从而导致系统的制冷功率和效率较低。U型气液谐振器中由于液体工质相对于气体工质具有较高的密度和较大的声学惰性，故U型气液谐振器相比传统气体谐振管具有较高的压力振幅和较低的工作频率。因此，气-液耦合双作用行波热声制冷系统具有起振温度低、运行频率低、压比大、效率高等优势，适用于对低品位热能的利用。

基于此，本节模拟了三级气-液耦合双作用行波热声制冷系统的性能参数变化，系统运行频率为13 Hz，如图3～图5所示。给定热声发动机热端温度为400 K，热声制冷机冷端温度为270 K，环境温度为293 K，系统平均压力为1 MPa。

图3所示为三级气-液耦合热声制冷系统的声功及压力波和体积流率相位差的沿程分布。由图3可知，基本单元的进出口声功大致相同，约为247 W，声功在热声发动机处由于回热器中的热致声效应被放大，在热声制冷机处因声致冷效应而降低，剩余声功传递到U型气液谐振器处进行调相，由于液体振子阻尼的存在，声功略有降低。由于水冷器的流道与空管段存在突变截面，声功存在部分损失。压力波和体积流率的相位差从入口的-35°变为气液谐振器前的55°，经过谐振管和后连接管又逐渐变回-35°在发动机和制冷机的回热器中，相位差均处在较好的行波声场，有利于系统实现高效的热声转换。

图3 三级气-液耦合热声制冷系统声功和相位差沿程分布Fig.3 Acoustical power and phase distributions of three-unit system

图4和图5所示分别为系统的压力波幅值和压力波相位以及体积流幅值和体积流相位的沿程分布。由图可知，系统的压力波幅值由于回热器阻力产生的压降损失较大，在发动机、制冷机的回热器中明显下降；经过气液谐振器时由于液体振子的作用增大，最终在谐振器末端变径管处增大为入口值。而压力波的相位只是在气液谐振器处减小了约 120°，流经其他部件基本不变。系统的体积流幅值在发动机的回热器中增加，而在制冷机回热器中减小。发动机和制冷机的进出口的体积流幅值大致相同，而系统体积流的相位角在系统中沿程逐渐减小，进出口相差为 120°。

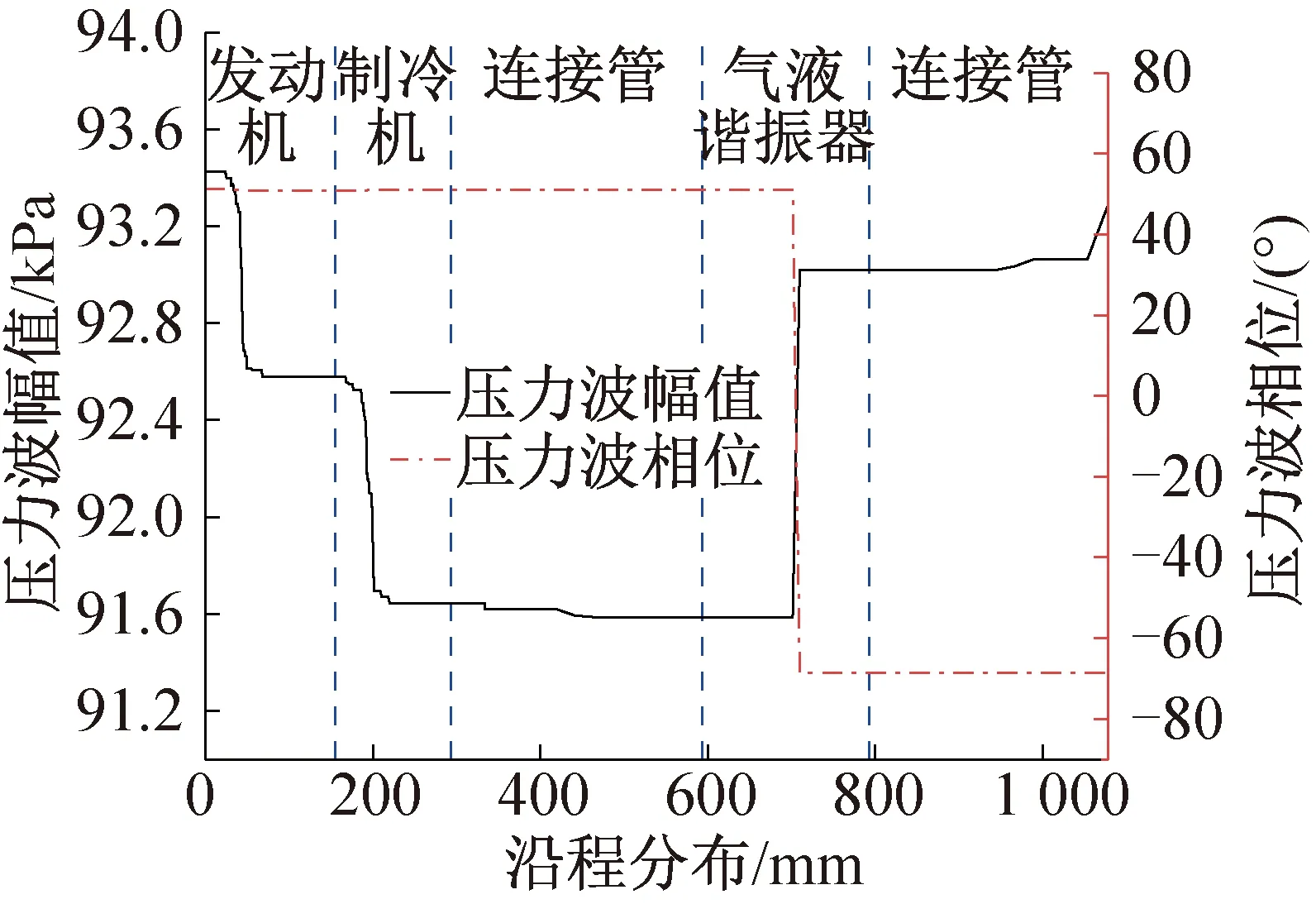
图4 系统压力波幅值和相位的沿程分布Fig.4 Distributions of oscillating pressure and phase

图5 系统体积流幅值和相位的沿程分布Fig.5 Distributions of oscillating flow and phase

2.4 多级系统性能模拟

2.4.1 定压多级热声制冷系统性能模拟

为了全面考察不同级数连成环路时系统的性能，本节分别模拟了三级、四级、五级和六级热声制冷系统，各级系统的基本单元尺寸不变，仅进出口的压力波和体积流率的相位分别相差120°、90°、72°及 60°。模拟中平均压力为1 MPa，热端温度为400 K，冷端温度为270 K，环境温度为293 K。

图6和图7所示为发动机和制冷机回热器进出口的相位差随环路级数的变化。由图可知，随着环路级数的增加，热声发动机回热器入口的相位差从-35°变为-25°，而回热器出口的相位差由-27°变为-21°。热声制冷机随着级数的增加，其进出口压力波和体积流的相位差呈下降趋势。当回热器中的相位差接近 0°时，更接近纯行波声场，回热器中的热力循环更接近可逆的斯特林循环，系统效率更高[18]。故当环路中级数较多时，热声发动机的回热器出口处相位差更接近0°，性能有所提升。

图6 不同级数发动机回热器的压力波和体积流的相位差Fig.6 Phase difference between pressure wave and volume flow of engine regenerators of different stages

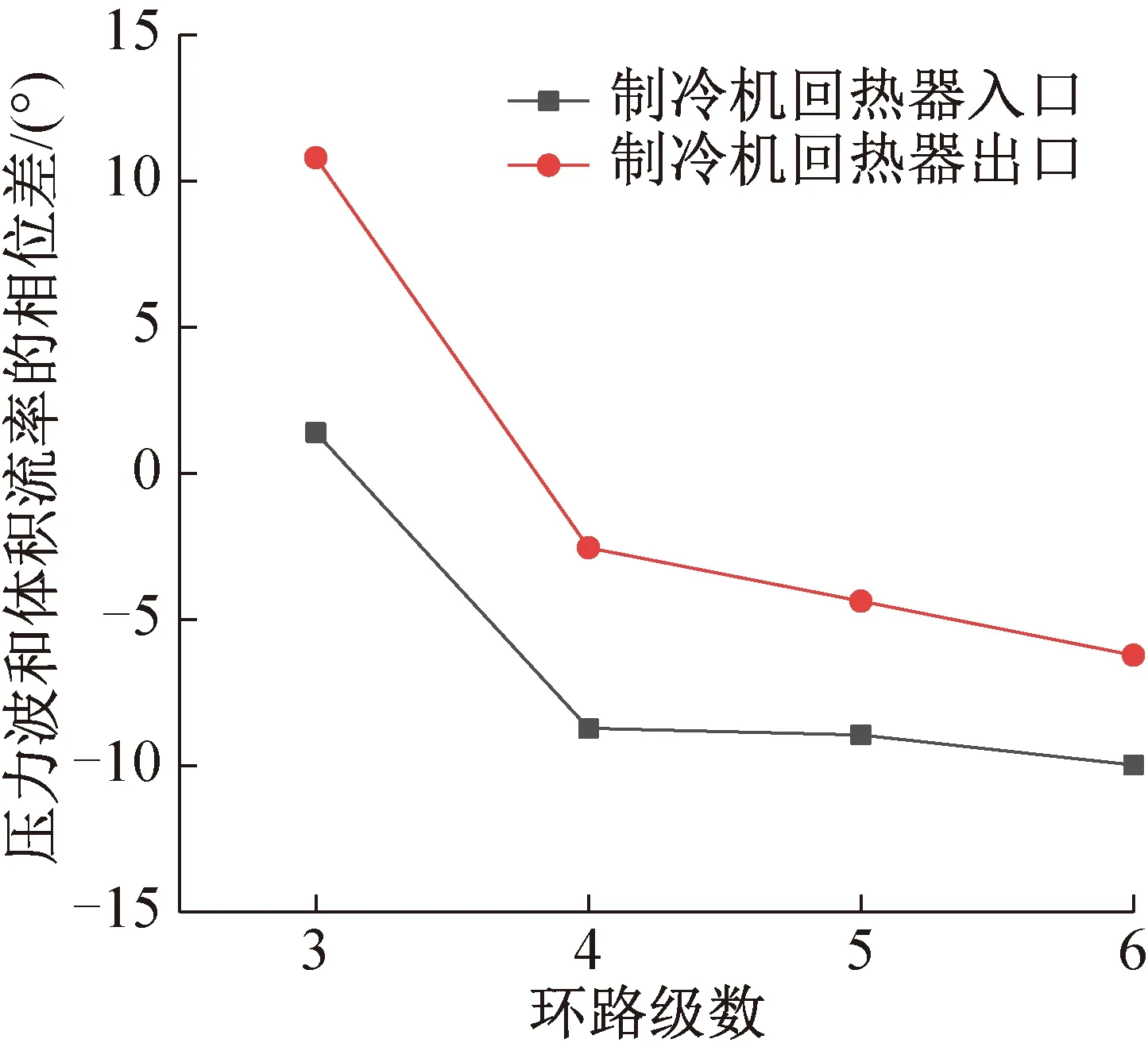
图7 不同级数制冷机回热器的压力波和体积流的相位差Fig.7 Phase difference between pressure wave and volume flow of refrigerator regenerator of different stages

图8所示为发动机回热器放大声功和热声转换效率随环路中级数的变化。由图8可知，随着级数的增加，回热器放大的声功不断增加，在级数为六级时达到最大值，说明在相同的温度梯度下，回热器放大声功的能力增强。而热声转换效率是指回热器放大的声功与加热量的比值，可综合性地反映发动机的性能[18]。热声转换效率随着级数的增加总体呈下降趋势，从23%降至 19%，单台发动机的性能整体呈下降趋势。

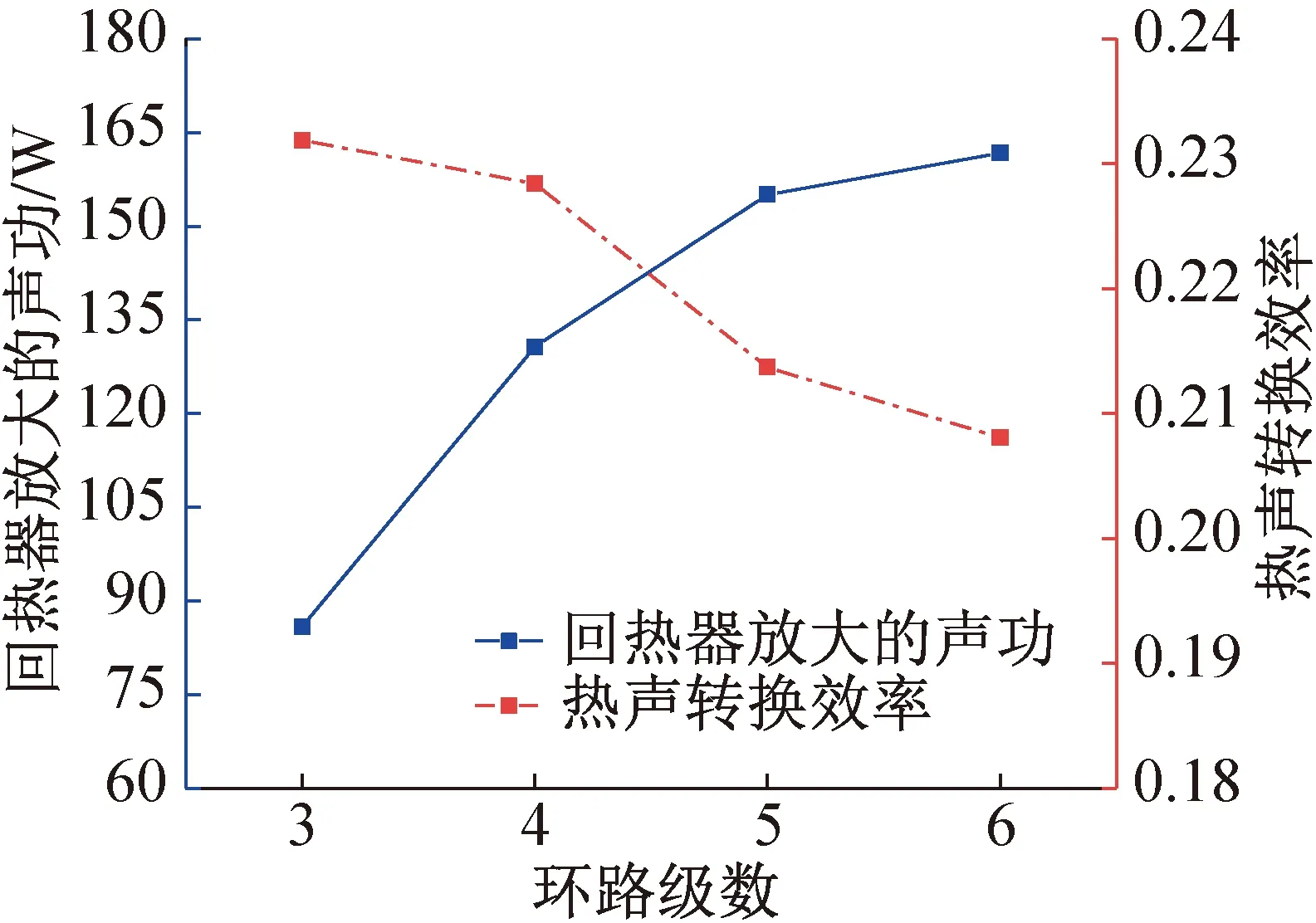
图8 回热器放大声功和热声转换效率随环路级数的变化Fig.8 Acoustic power and thermoacoustic conversion efficiency of the regenerator varies with the number of loop stages

图9所示为基本单元进出口压力波和体积流的幅值随环路级数的变化。由图9可知，由于每个基本单元参数分布均一致，所以进口与出口的压力波或体积流的数值是相同的。随着级数的增加，进出口压力波幅值从94 kPa升至113 kPa，体积流幅值从0.006 5 m3/s升至0.010 7 m3/s，二者的上升使发动机的声功及功率密度提高，整机功率密度提升。

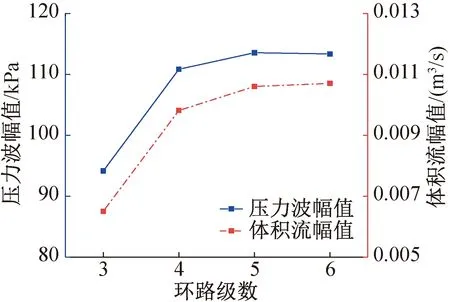
图9 压力波和体积流的幅值随环路级数的变化Fig.9 The amplitude of pressure wave and volume flow varies with the number of loop stages

2.4.2 平均压力对多级热声制冷系统的影响

热声制冷机中的功率密度与平均压力成正比。但平均压力越高，容器的刚度要求越高，成本更高。同时，系统平均压力越高，热渗透距离越小，对回热器的要求也更高。为了全面考察不同级数系统在不同压力下的运行情况，本节将通过改变系统的平均压力来模拟不同级数系统的性能参数。

图10所示为平均压力对多级系统热力性能的影响。由图10可知，增加平均压力可使系统的加热量显著增加。当平均压力低于5 MPa时，压力对制冷量的影响较大，而对COP的影响较小，始终保持在0.5～0.7的范围内。当平均压力较高时，系统制冷量随平均压力的增加而缓慢上升，COP受压力的影响显著下降。此外，系统级数越高，声功利用率越高，使系统制冷量增大，COP降低。当系统平均压力达到10 MPa时，六级系统的制冷量达到最大值16.1 kW，COP为0.38。该结果表明气-液耦合热声制冷系统在大功率制冷方面有良好的应用潜力。

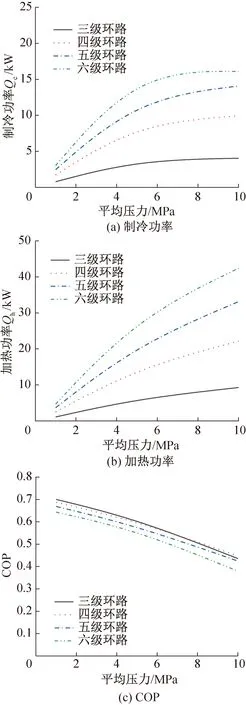
图10 平均压力对多级系统热力性能的影响Fig.10 The effect of average pressure on the thermal performance of a multi-stage system

3 结论

本文提出一种新型气-液耦合双作用行波热声制冷系统，并进行了数值模拟，研究系统的重要性能参数，得到如下结论：

1)三级气-液耦合双作用行波热声制冷系统的声功沿程分布较为理想，压力波和体积流率的相位差处于良好的行波相位。在平均压力为1 MPa，加热温度为400 K，制冷温度为270 K，环境温度为293 K时，系统运行频率为13 Hz，制冷量为0.78 kW，COP为0.7，系统相对卡诺效率达到22.3%。

2)对于不同级数的气-液耦合双作用行波热声制冷系统，随着级数的增加，系统发动机回热器的出口处相位差更接近0°，热力循环更接近理想的热声转换循环；发动机进出口压力波幅值从94 kPa升至113 kPa，体积流幅值从 0.006 5 m3/s 升至 0.010 7 m3/s，使声功及功率密度提高，系统整体性能提升。但系统级数增加，热声转换效率总体呈下降趋势，从23%降至 19%，单台发动机性能下降。

3)系统的平均压力越高，制冷量显著增加，但平均压力对COP的影响较小。系统级数越高，制冷量的增幅越大。平均压力为10 MPa时，六级系统的制冷量达到最大值16.1 kW，COP为0.38。