不同解算策略对PPP的影响研究

常 晶

（华北理工大学矿业工程学院，河北 唐山 063210）

王涛涛等[1]根据精密单点定位原理，对4种不同时长（30 min、1 h、2 h、24 h）的GNSS观测数据进行了RTKLIB精密单点定位测试，分析了RTKLIB单点定位精度与时长的量化关系，并给出了实用性高的参数组合。管真等[2]分析了GNSS卫星星历几种类型的精度，并对精密星历进行了详细分析，将超快星历、快速星历和最终星历对比后得出，快速星历在精度上比较接近最终星历，通过对比常用的几种卫星坐标插值拟合方法，认为采用Chebyshev多项式拟合方法对精密星历进行拟合插值，拟合效果比较好。何一辛等[3]利用IGS不同分析中心提供的精密轨道和钟差产品，对全球分布的15个跟踪站进行精密单点定位解算得到了德国地学研究中心（GFZ）、欧洲航天局（ESA）及欧洲定轨中心（CODE）的产品较为优秀而且在实际PPP解算时应注意提高轨道产品精度。程贇等[4]利用ICS提供的综合精密产品和不同分析中心的精密产品，比较分析了不同分析中心精密轨道和精密钟差产品的区别，并基于RTKLIB比较不同分析中心精密产品PPP单天解相对于IGSPPP单天解的点位分量误差，得出尽管不同分析中心的精密轨道和精密钟差产品存在差异，但采用同一分析中心精密产品进行精密单点定位时，其X、Y、Z坐标分量偏差均在mm级，其点位定位误差在2 mm～8 mm之间波动，而且同一分析中心的轨道和钟差产品具有自洽性和一致性。

1 RTKLIB精密单点定位算法分析

1.1 RTKLIB介绍

RTKLIB软件选择精密单点定位算法的情况下，解算步骤包含资料提取和处理、信息预处理、观测建模以及误差修复等。

在全球导航卫星系统GNSS中，RTKLIB属于重要标准，其来源于日本东京海洋大学，关键的功能如下。

1）允许各类GNSS系统的基础以及精密定位算法，尤其是GPS、GLONASS等。

2）允许各类GNSS实时以及后处理模式，具体有单点定位、DGPS/DGNSS等。

3）允许各类GNSS标准格式以及协议：RINEX2.10、RINEX2.11等。

4）允许各类GNSS接收装置专用数据协议模式：OEMStar、NVS等。

1.2 RTKLIB精密单点定位解算流程

RTKLIB内部借助GPST（GPST时间）应用到GNSS的数据处置以及定位算法方面。数据从RTKLIB内展开处置前，应当调整成GPST时间。选择GPST的主要因素在于防范处理润秒。接收装置以及卫星的方位从RTKLIB内体现成ECEF坐标体系里的X、Y、Z轴。但是，能够评估精密单点定位准确性的坐标属于接收装置方位的本地坐标，即ENU坐标，这一坐标基本从GNSS导航处理。基于此，ECEF坐标至本地ENU坐标存在转换的问题，其转换能够借助旋转矩阵解决。

RTKLIB的算法完善，导航以及定位能力卓越，能够解决各类GNSS定位解算。从该软件内执行精密单点定位需要依赖于RTKPOST功能组，其中涉及六个方面，能够实现资料提取和处理、模糊度运算等功能。RTKLIB精密单点定位的算法流程如图1所示。

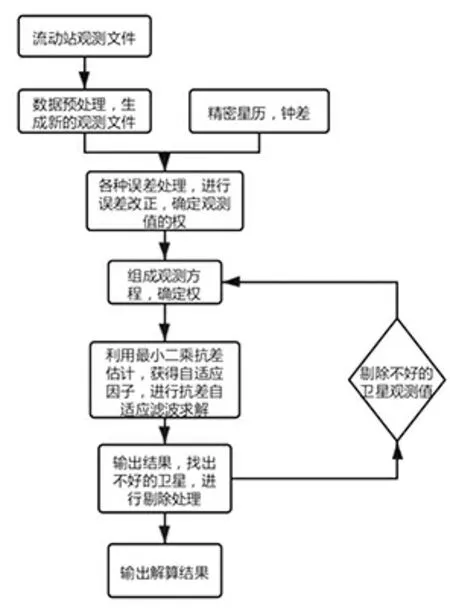
图1 RTKLIB精密单点定位算法流程图

2 不同解算策略对精密单点定位性能的影响分析

本实验采用2015年1月1日JFNG站的观测数据。试验的具体策略如下。

1）先后借助向前、向后滤波展开了GPS-PPP静态定位。

2）分别选取了15°、20°、30°和45°四个值进行GPSPPP静态定位。

3）分别使用精密单点定位静态解算模式（PPP Static）、精密单点定位动态模式（PPPKinematic）进行比较。

4）不同对流层模型GPS-PPP静态定位。

2.1 不同滤波方法对PPP收敛速度和定位精度的影响

为研究各种滤波方式在PPP收敛效率以及定位准确性上的作用，图2提到测站前/后向滤波GPS-PPP的定位情况。具体来看，E、N、U三种路径当中，前向滤波方式收敛效果优于后向滤波，但是从稳定性以及精度两个层面的差异不明显，对于RMS值，在测站前向滤波GPS-PPP当中，RMS数据均低于后向滤波，并且，两种测站RMS数据也没有超过3 cm。所以，前向滤波法有利于增强收敛效率。在RMS数据来看，E路径中，前向滤波法可以实现更低的RMS值，由此让PPP精度有所提高，然而，N和U方向前向滤波法对PPP精度改善略差于E方向。所以，从展开PPP数据处理的阶段借助前向滤波法能够提升PPP收敛效率，降低收敛的时间损耗，并且在精度方面起到了优化作用。

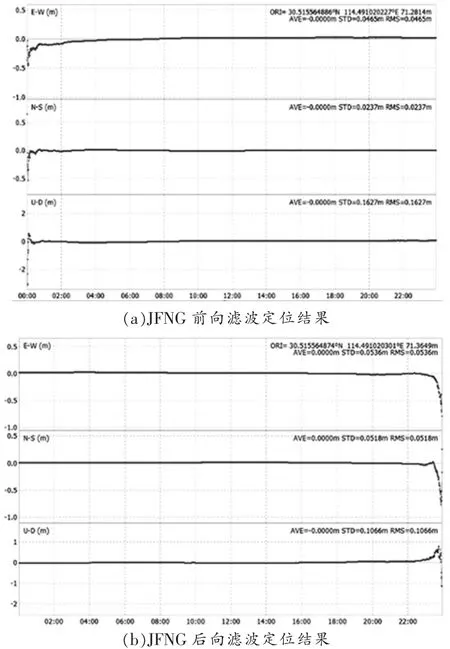
图2 前/后向滤波PPP定位解算精度对比分析

2.2 不同卫星截止高度角对PPP收敛速度和定位精度的影响

卫星截止高度角主要作用在于限制遮挡物，或者多线路效应下建立的蔽遮高度角，没有达到这一角视空域的卫星无需追踪。

从展开精密单点定位静态运算阶段，卫星截止高度角能够干预测站关于卫星的观察时间，并且还能影响观测信息，而观测信息属于精密单点定位的重要参考依据。另一方面，卫星截止高度角有差异的情况下，精密单点定位阶段各方面误差也会有一定的区别，其共同干预精密单点定位最后的运算精确性。

本实验选择2015年1月1日JFNG站的观测值，展开PPP静态解算，确定15°、20°、30°、45°四个高度角，FNG测站的不同卫星截止高度角下PPP定位解算精度对比分析如图3所示。

图3 JFNG测站不同卫星截止高度角下PPP定位解算精度对比分析

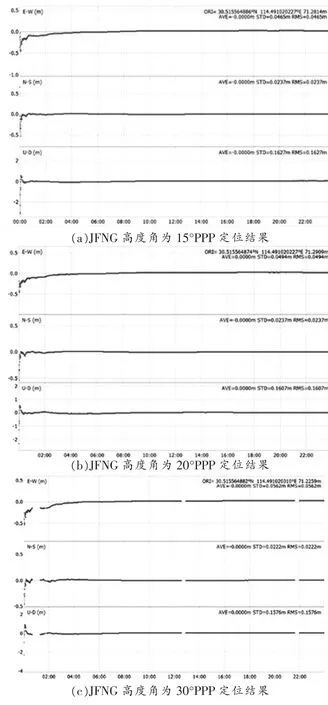
根据上图能够得知，在各种截止高度角中，PPP收敛时间有一定的拉长，15°、20°的收敛时间较为相同，在0.5 h左右，如果高度角设定成30°的情况下，收敛时间拉长，基本处在1 h，如果高度角在45°情况下，解算缺乏稳定性，定位同样也面临干预。

2.3 不同解算模式对PPP收敛速度和定位精度的影响

RTKLIB中有三类PPP解算方式，具体为静态解算模式、动态模式和固定模式。

1）静态精密单点定位属于目前最为普遍的一种定位模式，借助各个频率观测数据的相互结合，产生组合观测值，应对其中误差，增强定位精度，不过考虑到参数估算方式难以解决高动态数据，从实践上存在局限。

2）动态精密单点定位模式。主要的原理在于借助MGEX精密星历等，基于接收装置的观测信息展开动态非差处置，实现精度要求。因为在独立性、动态性等方面的优势，该技术从高精度动态应用方面体现了不可替代的作用。

实验纳入了JFNG站2015年1月1日的测量信息，精密星历主要选择IGS提到的15 min间距的轨道以及钟差产品，具体名为igs18775.sp3。

本实验依托于GPS单系统实施，而最后的结果储存于格式为.pos的文件内，结合RTKPLOT系统表现详细的定位结果，FNG测站的不同定位模式下PPP定位结果精度分析如图4所示。

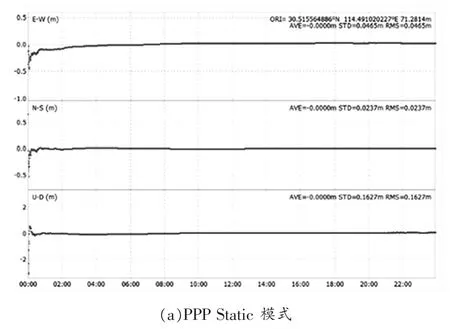
图4 JFNG测站的不同定位模式下PPP定位结果精度分析

根据上图能够发现，两类定位模式均可以实施PPP解算，不过，E、N、U三种路径当中的误差图显示，基于PPPStatic模式，输出结果相对PPPKinematic更平稳。在误差程度上展开对比，PPPKinematic仅可以满足亚米级精度要求，不过PPPStatic可以达成厘米级精度需求。

2.4 不同对流层模型对PPP收敛速度和定位精度的影响

涉及对流层干延迟误差的问题，一般应用ztd-est等模型，而对流层湿延迟误差更加适用于随机游走。

图5先后体现了JFNG测站不同模型的GPS-PPP静态定位误差情况。基于图5，选择Saastamoinen模型的情况下，表现在PPP收敛速度以及精度方面的作用明显，误差和其余模型对比之下更差，尤其是U路径中的误差和其余两条路径对比更大，而选择Estimate ZTD、Estimate ZTD+Grad的情况下，误差更加可控，收敛效率更高，同时，两个对流层模型收敛周期以及精度基本一致，Estimate ZTD+Grad表现出轻微的优势，且两个模型的RMS数据都不超过2 cm，而Saastamoinen模型无法控制到3 cm内。

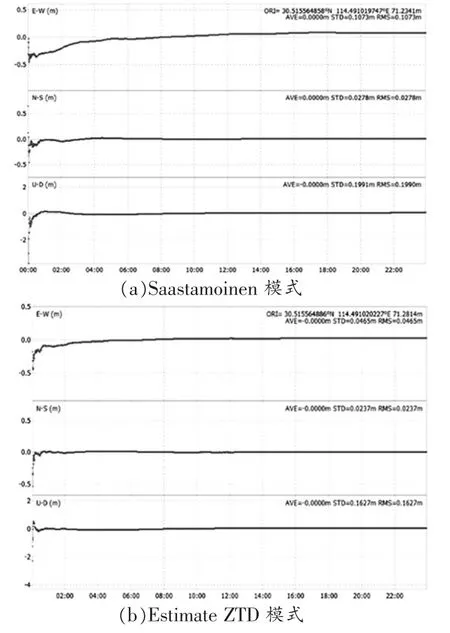
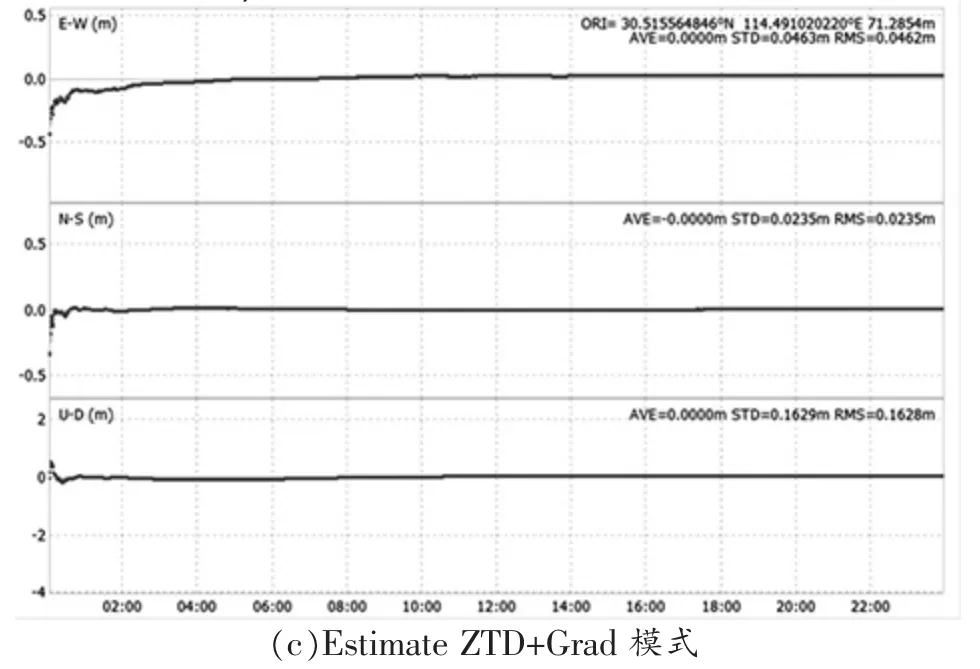
图5 JFNG测站的不同对流层改正模型下PPP定位结果

3 结论

通过不同解算策略对精密单点定位功能的影响探究，发现在实施PPP数据处理的阶段，借助前向滤波法能够增强PPP收敛能力，并且在定位精度方面存在优化作用；卫星截止高度角在30°范围内几乎不考虑PPP收敛方面的影响，若大于30°，则收敛速度和高度角反向变动；在PPP解算中，如果与Kinematic模式对比，Static模式定位存在一定的精度优势；选择Saastamoinen模型的情况下，PPP收敛速度、精度将面临显著的影响。从RTKLIB软件来看，主要对周跳展开测量，但不展开修正，其算法的优化有待探究。