基于导引图像滤波和截断全变分的CT重建算法

时鸿雁， 吴爱弟， 冀东江

(天津职业技术师范大学 理学院， 天津 300222)

0 引言

根据采集到的投影数据，利用重建算法重建出待检测样品的内部结构，这项技术称为计算机断层成像技术(Computed Tomography，CT)[1]。解析重建算法和迭代重建算法是两种常用的图像重建算法。其中滤波反投影重建算法(Filtered Back Projection, FBP)[1]属于解析重建算法，代数重建算法(Algebraic Reconstruction Technique, ART)[3]和联合代数重建算法(Simultaneous Algebraic Reconstruction Technique, SART)[4]属于两种常见的迭代重建算法。在投影数据不完整或噪声较大的情况下，与解析重建算法相比，迭代重建方法可以重建出更好的结果。迭代重建算法的优势是可以将先验信息融合到重建图像过程当中，在实际应用过程中，常常采用正则化技术来引入先验信息以提高重建图像的质量。潘晓川[6]等将TV作为正则项引入到ART算法中，重建后得到的图像质量更好，但是对于具有更多图像纹理细节和复杂边缘结构的图像，将导致重建的图像过度平滑。后来Dou[7]等提出了截断全变分用于图像平滑，截断TV去除不重要的细节的同时还可以保留显著的边缘，而且它仅对图像的部分梯度进行惩罚，由此可以解决TV对较大的梯度幅度进行惩罚而导致的过度平滑的问题。因此，我们可以将截断TV作为正则项用于图像重建。

何凯明等[8]提出了导引图像滤波，它能更好的利用导引图像的结构，把导引图像含有的重要特征转移到输入的图像中，并让滤波后的图像保留输入图像的部分信息。冀东江等[9]提出了基于导引图像滤波的联合代数重建算法，在图像重建过程中更新先验指导图像，迭代地合并信息，提高了重建图像的质量。余维等[10]提出了一种稀疏性诱导的动态引导图像滤波算法。该算法利用引导图像滤波，把SART算法重建的图像作为输入图像，TDM-STF算法重建的图像作为导引图像，以解决有限稀疏角CT图像重建问题。

受上述研究的启发，我们提出了一种基于导引图像滤波和截断全变分的CT重建算法。我们把SART算法重建的图像当作输入图像，基于截断TV最小化后的图像当作导引图像，采用导引图像滤波来处理稀疏角CT重建问题。这样既利用了基于截断TV的图像重建算法具有保护强边缘的作用，又发挥了具有保护边缘和平滑图像作用的导引图像滤波能传递图像特征的优势。本文使用SART算法、SART-TV算法、SART-TTV算法、SART-TV-GIF算法和SART-TTV-GIF算法分别在30个投影、45个投影、和90个投影下重建高分辨率的头部模型。SART-TTV-GIF算法可以有效地抑制噪声，减少伪影并更好地还原图像的边缘细节。

1 算法

SART算法

CT图像重建是一个典型的逆问题，实质上是求解线性方程组:

Af=p

(1)

式中,A=(aij)M×N为系统投影矩阵；aij为第j个像素对第i条射线对应投影值贡献的权系数；f=(f1,f2,…,fN)Τ为待重建图像；p=(p1,p2,…，pM)Τ,pi为第i条射线所对应的投影值;N为图像像素的个数。

SART重建算法的基本思想如下:在迭代更新的过程中，先计算每个扫描旋转角度下经过某一像素点的全部射线的误差值，再对这些误差值进行加权平均。该算法的迭代公式可以表示如下[4]:

(2)

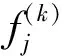
1.2 截断TV

Dou等提出了一种新的正则化方法，称为截断TV[7]。它可以有效的减少不重要的细节，保留显著的边缘，且不会造成图像过于平滑。

截断TV表示为[7]:

(3)

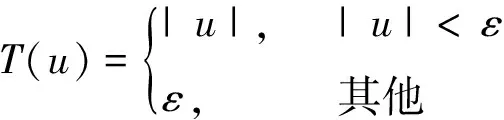
(4)

式中，u为平滑的结果图；(ux,uy)为u的梯度。截断TV只会惩罚幅度小于阈值ε的梯度，而对于大于阈值ε的梯度不会进行惩罚。

1.3 导引图像滤波

导引图像滤波已被广泛用于噪声减少、伪影去除、图像增强和图像重建。它是一种自适应权重过滤器，可以平滑图像并同时保持边缘。GIF中的重要假设是滤波器输出的图像fout能在一个正方形窗口i内被导引图像Iguide线性表示。即导引图像滤波的输出图像fout如下所示[8]：

(5)

式中，ak和bk在以像素点k为中心且半径为r的正方形窗口wk中是常数。另外，ak和bk系数是通过最小化下面的能量函数来求解的：

(6)

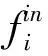
1.4 SART-TTV-GIF算法

SART-TTV-GIF算法的求解步骤如下。

(1)SART步骤

SART-TTV-GIF算法的第一个步骤是使用SART算法进行投影与反投影运算来迭代更新图像：

fn=SART(fn-1)

(7)

(2)TTV步骤

SART-TTV-GIF算法第二个步骤是求解截断TV的最小值问题。目标函数如下所示:

(8)

式(8)的左边第一项是数据保真项，第二项是截断TV。其中截断TV是非凸面的，并且由于其“截断的”形状而难以优化。但是可以使用L0正则化来重新表达。以ε为参数，在(4)中定义的T(u)等价于

φ(u,l)=min{ε|l|0+|u-l|}

(9)

式中，|·|0为零次幂运算符，即如果l≠0则|l|0=1，否则|l|0=0。

式(9)又等价于

(10)

(11)

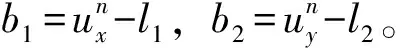
用拉格朗日乘数并引入布雷格曼距离，式(11)转化为：

(12)

上述联合最小化问题可以通过将其分解为几个子问题来交替解决，如下所述：

①固定l1,l2,b1,b2,t1,t2来计算un

(13)

得出欧拉-拉格朗日方程:

fn-un+

(14)

式中，Δ为拉普拉斯算子，式(12)可用高斯-赛德尔迭代算法或者FFT算子快速求解。

由图8可见，随着聚乙烯靶高度的增加，中子探测效率增加，中子能量分辨率变化不大。因此，在聚乙烯靶高度方向(图1中y方向)，应尽量选择尺寸大的聚乙烯靶，这样可以在保持能量分辨率的条件下，提高中子探测效率。

②固定un,l1,l2,t1,t2来计算b1,b2

应用收缩算子获得该子问题的唯一极小值：

(15)

(16)

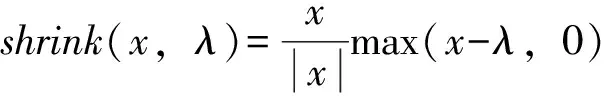
③固定un,l1,l2,b1,b2来更新t1,t2

(17)

(18)

④固定un,t1,t2,b1,b2来更新l1,l2

(19)

这个子问题的解决方案是

(20)

(21)

(3)GIF步骤

(22)

(23)

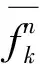
(24)

表1 SART-TTV-GIF算法的主要步骤

2 图像结果的评价

本文是对重建的图像进行客观评价，就是通过选取峰值信噪比(PSNR)[11]和均方误差(MSE)[11]来对重建图像的降噪能力和精度等方面进行分析。其中，PSNR的值越大，MSE的值越小，重建图像的质量越高。其计算公式如下[11]:

(25)

(26)

式中，ti,j,ri,j分别为原图和重建图像在像素处的像素值；MAX1为原图的最大像素值。

3 实验与分析

本文对高分辨率的头部模型[12-13]进行了仿真模拟,实验需要在如下环境下进行：Windows10操作系统，处理器为AMD RyZen 5 2500U with Radeon Vega Mobile Gfx 2.00 GHz，8.00 GB内存，Matlab R2018b，对大小为243×243的图像进行重建。

3.1 无噪声实验

本文在180°范围内等间隔采样了90个投影、45个投影和30个投影，分别对SART算法、SART-TV算法、SART-TTV算法、SART-TV-GIF算法和SART-TTV-GIF算法来进行实验。为了让不同算法之间的比较更为公平，这五种算法的最优参数和迭代步数都是通过评价指标和视觉效果的最优来选取的。表2所示为这五种算法分别在30个投影、45个投影和90个投影下的参数值的选择。

表2 参数值的选择

续表

如图1～图4所示，橘色箭头指出的重建图像的区域有明显的伪影。图1为头部肿瘤模型，原始模型中自带有高斯噪声[12]。在90个投影采样下，五种算法重建得到的图像都相对较好，但SART算法重建得到的图像边界模糊，SART-TV算法和SART-TV-GIF算法重建得到的图像边界较为清晰，SART-TTV算法和SART-TTV-GIF算法重建得到的图像边界最为清晰。在45个投影采样下，SART算法重建得到的图像有明显的噪声，重建得到的图像质量不好；SART-TV算法和SART-TV-GIF算法重建得到的图像有多处边缘伪影；SART-TTV算法重建得到的图像存在相对较少的伪影；SART-TTV-GIF算法重建得到的图像几乎没有伪影，质量更好。在30个投影采样下，SART算法重建得到的图像有严重的噪声；SART-TV和SART-TV-GIF算法重建得到的图像有很多伪影；SART-TTV算法重建得到的图像有较多的伪影；SART-TTV-GIF算法重建得到的图像几乎没有伪影，重建结果更好。在多个稀疏角度下，通过SART-TTV-GIF算法重建的图像质量更高，边缘伪影更少，能更好地保护边界结构。

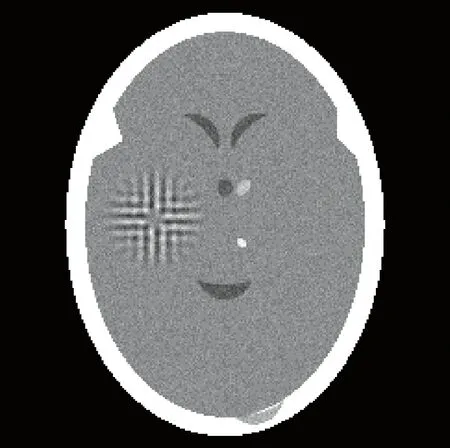
图1 参考图像

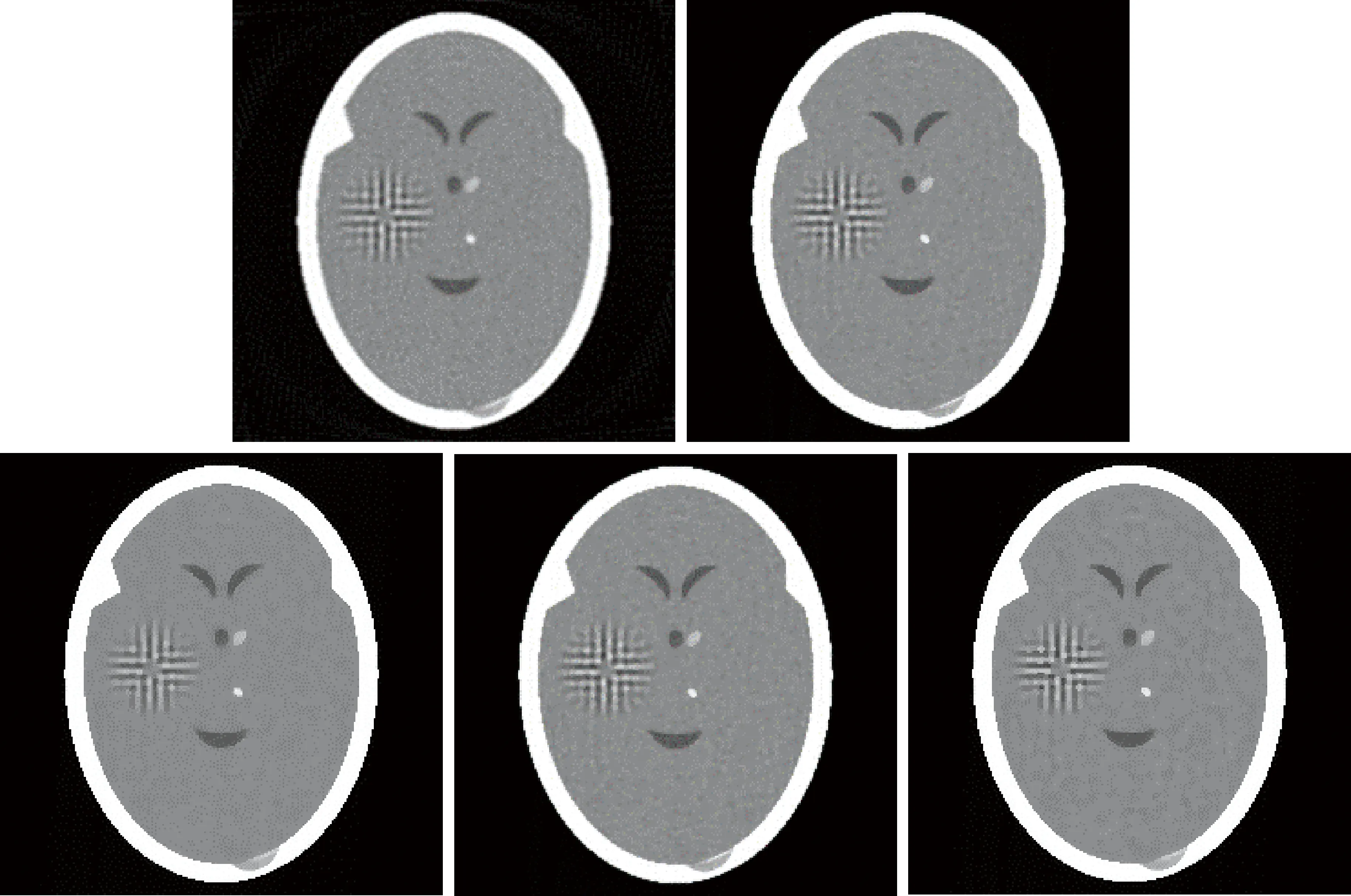
图2 90个投影(SART、SART-TV、SART-TTV、SART-TV-GIF、SART-TTV-GIF)

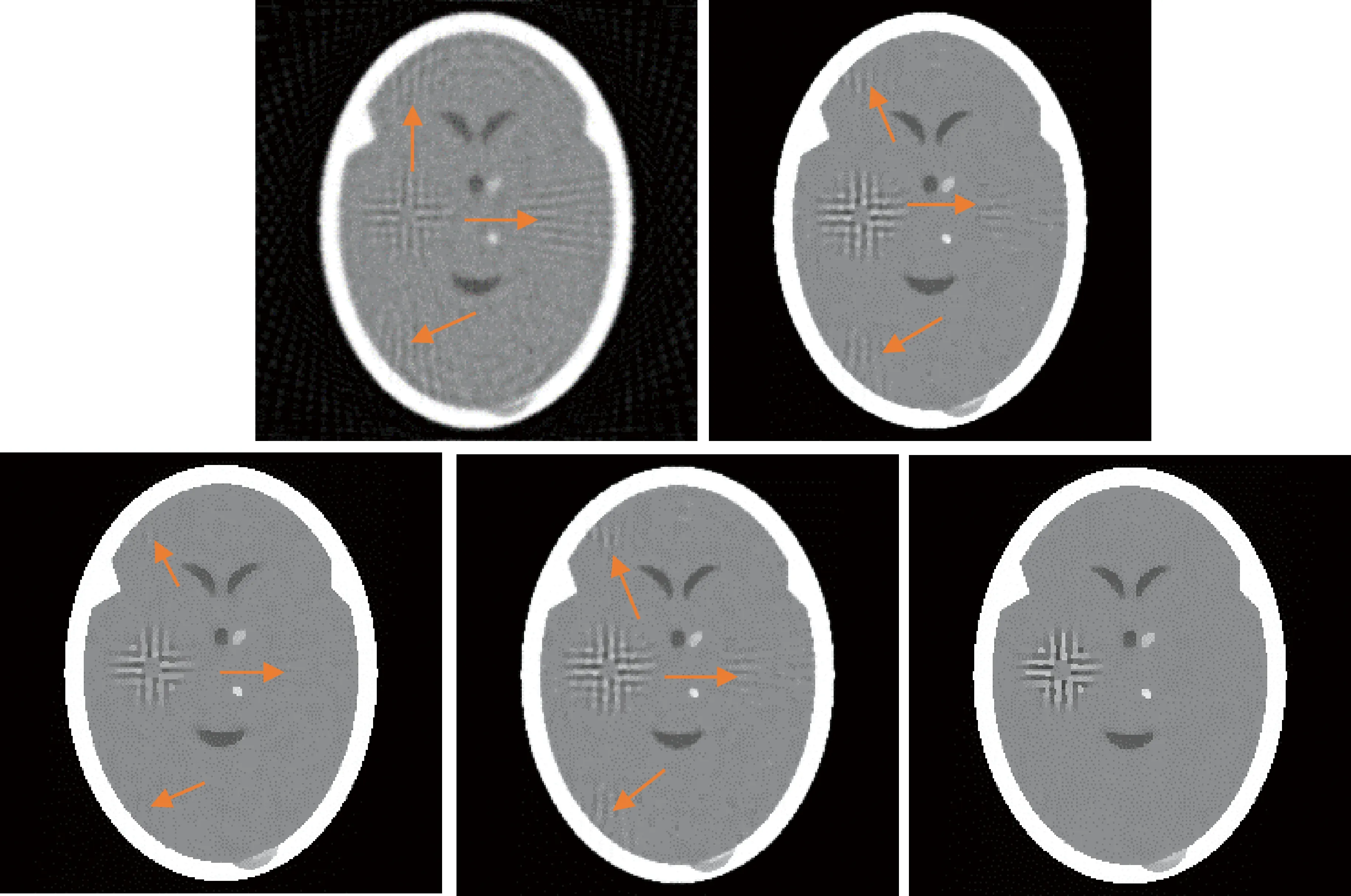
图3 45个投影(SART、SART-TV、SART-TTV、SART-TV-GIF、SART-TTV-GIF)

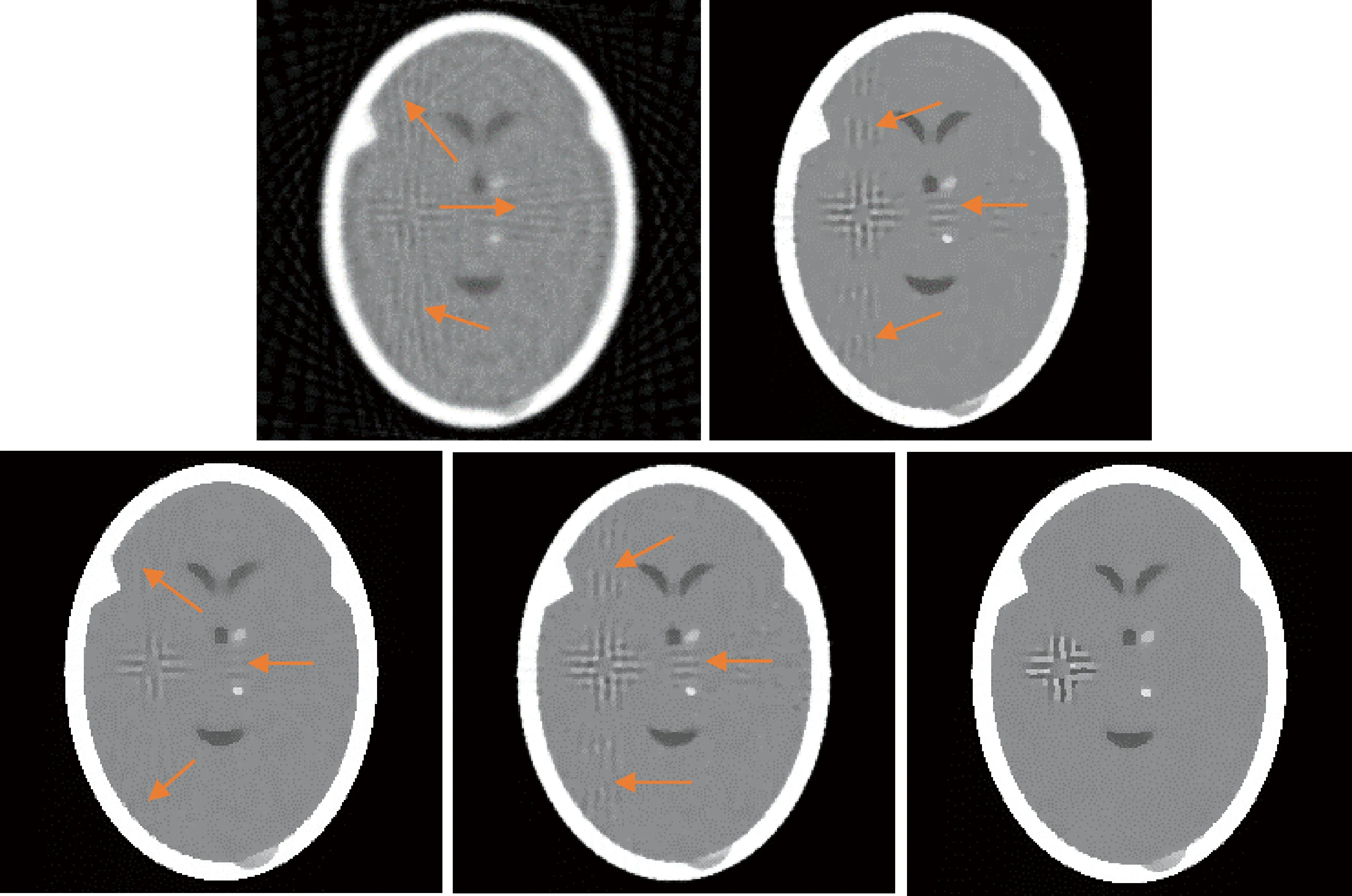
图4 30个投影(SART、SART-TV、SART-TTV、SART-TV-GIF、SART-TTV-GIF)

表3所示为对高分辨率的头部模型重建结果的评价。

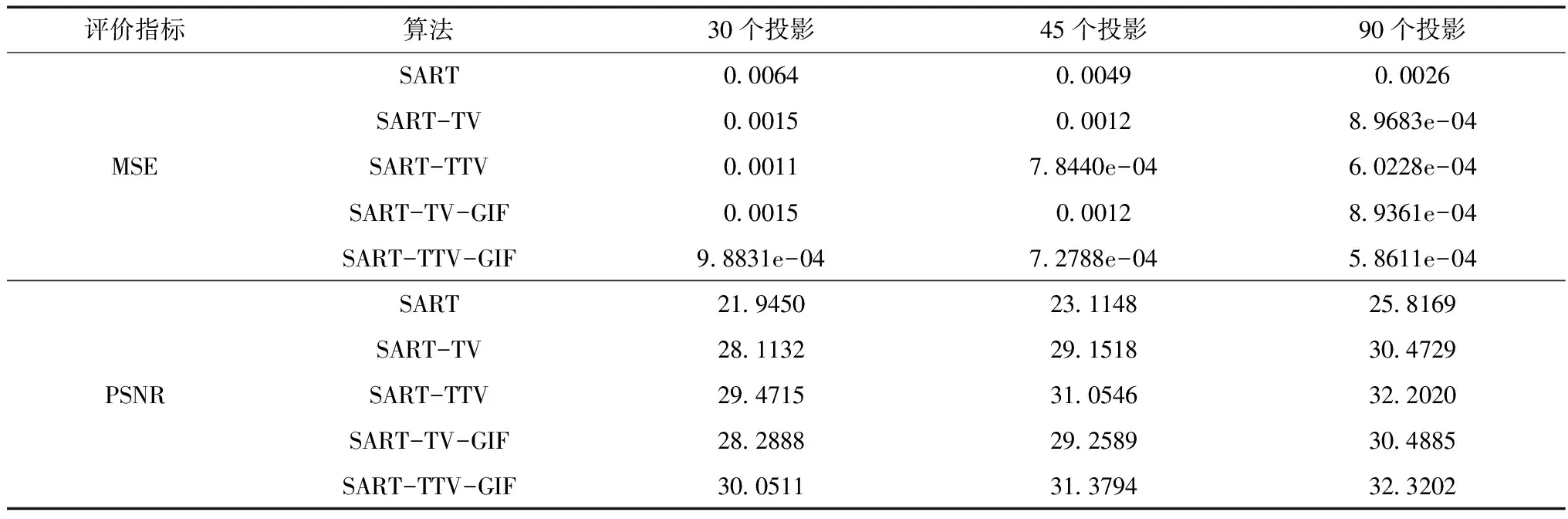
表3 图像重建结果的评价

从表3可以清楚地看到，SART-TTV-GIF算法的MSE值最小，而PSNR值最大。所以，在这五种算法中，SART-TTV-GIF算法的重建效果最好。

3.2 加噪声实验

在实际的应用中，探测器采集到的投影数据通常是含有噪声的。因此，我们向模拟的投影数据中添加了泊松噪声，入射的X射线光子个数为1.0×103，添加泊松噪声的均值为0。添加噪声后各个算法的参数值的选择如表2所示。

如图5～图7所示，随着向模拟投影数据中添加泊松噪声，不同算法重建图像的质量都有所降低。在90个投影采样下，五种算法重建得到的图像都相对较好，但SART算法重建得到的图像边界模糊，SART-TV算法和SART-TV-GIF算法重建得到的图像边界较为清晰，SART-TTV算法和SART-TTV-GIF算法重建得到的图像边界最为清晰。在45个投影采样下，SART算法重建得到的图像有明显的噪声和伪影，重建得到的图像质量不好；SART-TV算法和SART-TV-GIF算法重建得到的图像有很多伪影，SART-TTV算法重建得到的图像有较多的边缘伪影；SART-TTV-GIF算法重建得到的图像几乎没有伪影，质量更好。在30个投影采样下，SART算法重建得到的图像有严重的噪声和伪影；SART-TV算法和SART-TV-GIF算法重建得到的图像有较为严重的伪影，SART-TTV算法重建得到的图像有相对较少的伪影；SART-TTV-GIF算法重建得到的图像则存在少量伪影。在多个稀疏角度下，通过SART-TTV-GIF算法重建的图像质量最高，伪影更少,能更好的保留边界结构。

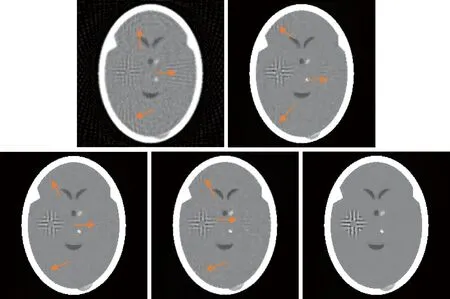
图5 90个投影(SART、SART-TV、SART-TTV、SART-TV-GIF、SART-TTV-GIF)(含噪声)

图6 45个投影(SART、SART-TV、SART-TTV、SART-TV-GIF、SART-TTV-GIF)(含噪声)

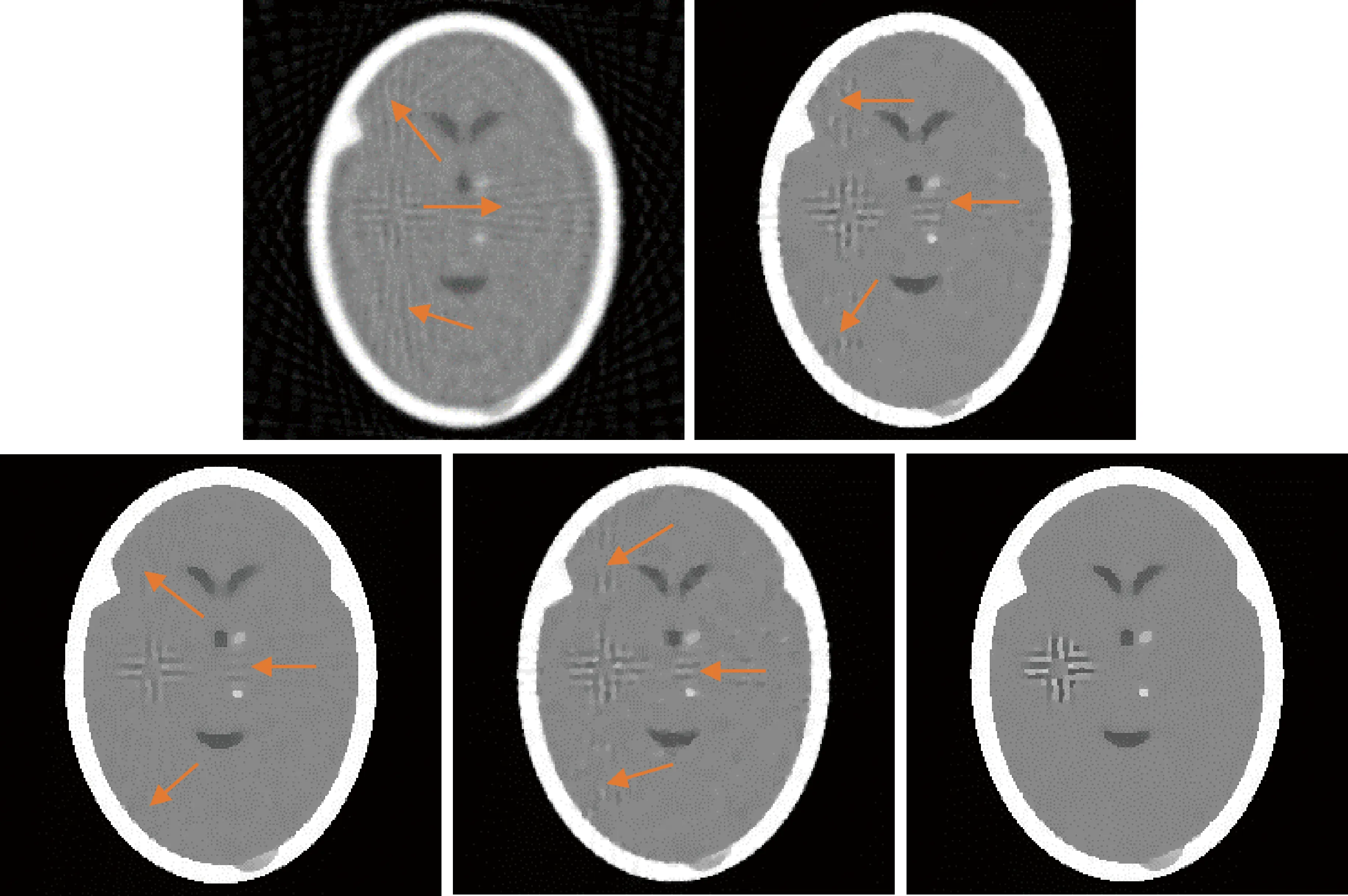
图7 30个投影(SART、SART-TV、SART-TTV、SART-TV-GIF、SART-TTV-GIF)(含噪声)

表4所示为对添加泊松噪声的高分辨率的头部模型重建结果的评价。表4与表3相比，MSE的值全都变大，PSNR的值全都变小，可以得出对图像添加噪声后，各个算法的重建图像质量普遍偏低。

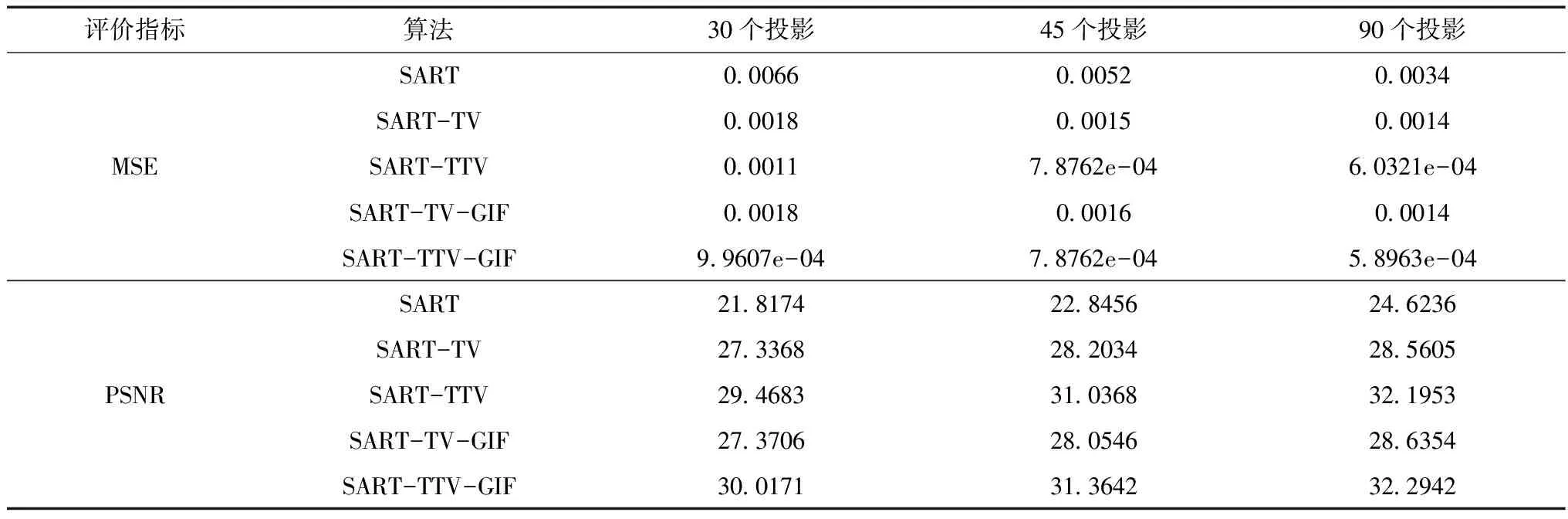
表4 含噪图像重建结果的评价

从表4可以清楚地看到，SART-TTV-GIF算法的MSE值最小，而PSNR值最大。所以，在这五种算法中，SART-TTV-GIF算法的重建效果最好。

4 结论

本文利用五种图像重建算法对高分辨率的头部模型进行了仿真实验，对稀疏角投影数据进行了图像重建，并对各种算法的重建结果进行了比较。实验结果表明，SART-TTV-GIF算法得到的重建图像质量更高，可以有效抑制噪声，减少伪影，并能更好地保留边界结构，并且运行速度很快。但是，SART-TTV-GIF算法包含许多参数，调试起来很耗时。本文的参数都是通过反复的实验来选取的，而且本文仅对高分辨率的头部模型进行了测试。在未来的工作中，将进一步讨论参数的最优选取方式并测试各种模型以测试算法的有效性，同时也会研究将该算法应用到有限角CT重建领域当中。