农业机械化对中国种植业贡献率研究

吕雍琪，张宗毅，张萌

（农业农村部南京农业机械化研究所，江苏 南京 210014）

改革开放以来，第二产业和第三产业迅速发展，非农实际工资不断增加，农村人口向城市转移，农业劳动力老龄化、减量化问题严重，农业生产耕种收各阶段都需要大量的劳动力，人力的缺乏导致产量低下，且限制农民的生产规模。农业机械的使用提高了劳动生产率和资源利用率，大大减少了农业生产过程中劳动力的需求量[1-2]。农业机械替代人力劳动力，大幅降低了劳动力成本，释放的资金可以用于购买优质种子、化肥、农业机械以及学习其他农业生产技术，从多方面促进农业产出的增长[3]。中国农业机械总动力由1949年的8.1万kW增加到2018年的10.04亿kW，年均增长率为13.08%。种植业总产值由1949年的255.78亿元增加至2018年的4 711.15亿元（以1952年为基期）。1949—2018年中国种植业总产值与农业机械总动力均呈现递增趋势。为衡量农业机械化对种植业增长的贡献，把握我国种植业农业机械化发展效益，有必要定量测算农业机械化对种植业的贡献率。

农业机械化对种植业的贡献率即，将农业机械引入生产过程后创造的种植业产值增长率占种植业总产值增长率的比重[4]。常用的测算生产要素贡献率的主要方法可以归类为：主观指标法、贡献有无法和数学模型法[5-6]。主观指标法主要是特尔斐法和专家调查法，其算法简单，数据量小，但不确定因素、人为因素多，主观性强，使用较少。贡献有无法是项目评价方法的应用，测算有农业机械与无农业机械两种情况下农业总利润的差额，工作量大，难以精确估算农业机械在各个方面作用的产值增加量，适合范围较小地区的农业机械化贡献率测算[7]。数学模型法通过构建具体的生产函数对统计数据进行分析得出结论。常用于计算生产要素贡献率的生产函数主要有C-D生产函数[8]、索罗余值[9]和超越对数生产函数[10-11]等。C-D生产函数法无法确定劳动力与农业机械的投入比率，且受限于回归技术，适用于时间跨度较长的农业机械化贡献率测算[12-13]。索洛余值是生产函数的具体形式，采用一般表达式，通过数学推导，最终得出增长速度方程，因而测算结果更符合客观实际[14]。索洛余值法避开了具体生产函数形式的约束，但需要“希克斯中性”、“规模收益不变”的假设前提，条件苛刻。超越对数生产函数是对C-D生产函数的扩展，除了包含中性技术进步项、要素进步项以外，还包含要素交互项[15-16]。除以上方法外，孙福田和王福林[17]研究用数据包络分析法[18]的两种方法：C2R与C2GS2模型测算农业机械化对农业产出的贡献率，在考虑科技进步的情况下进行测算，使测算结果更趋于合理；王福林等[19]提出了一种基于增长速度方程的有约束农业机械化贡献率的测算方法。

已有关于农业机械化贡献率的测算，对象是中国整体或某一省份，时间为1～5年，缺乏农业机械发展进程中时间和空间上对比分析。中国幅员辽阔，各省之间地理情况、气候特征、经济条件有着较大差异，农机装备的分布、农业机械利用率、农机化发展质量不同[20]，改革开放至今，农业政策变化较大，用时间序列数据测算近几年某一省份的贡献率，不能体现变革对农业机械发展的影响。因此，本文利用省际面板数据，采用C-D生产函数法，运用变系数固定效应模型，测算各省和全国1979—2018年总体农业机械化对中国种植业贡献率，相对时间序列数据省际面板数据包含更多的个体行为信息，能够更精确测量各省份之间的差距，更能体现各省份不同时期贡献率变动情况。

1 研究方法

1.1 方法选择

本文运用C-D生产函数法测算农业机械化贡献率。C-D生产函数法是一种间接测算贡献率的方法，假设生产函数为柯布道格拉斯生产函数，通过取自然对数、回归求得各生产要素弹性，用弹性求解贡献率[21-22]。C-D生产函数法形式简单、便于计算，所以被广泛运用，并常用于测量科技进步率。

C-D生产函数在近年来遭受不少批评，认为该方法是一种“专横”的方法，且在测算农业机械化贡献率时，农机总动力构成复杂，无法分割，会产生误差[1]。但是，该方法的理论性质基本正确，因而是可以接受的[23]。另一方面，我国各省统计数据缺乏，其他模型需要的统计数据没有可靠的来源，所以用该方法测算农业机械化贡献率是合理的。

1.2 模型设置

影响种植业产出（Y）的生产要素主要有劳动力投入（L）、资本投入（K）、土地投入（D）等，其中资本投入用化肥施用量（F）与农业机械总动力（M）表示，则产出函数可以表示为：

式中：A为未体现在其他投入要素的综合技术水平，α、β、θ、γ分别为劳动力投入、化肥施用量（折纯量）、农业机械总动力、土地投入的产出弹性系数。μi和λt分别为个体效应与时点效应，εit为随机误差项。对生产函数两边取对数得：

通过线性回归可以求出各投入要素的产出弹性系数，其中第i省份农业机械化产出弹性系数为θi。若使用全国汇总数据进行回归，可以去掉时间效应和个体效应直接回归。

第i省份农业机械化对该省种植业的平均贡献率（δi）为：

式中：mi代表农业机械总动力年均相对增长，yi代表种植业总产出年均相对增长。年均相对增长用几何平均法得到。

全国农业机械化对种植业的总贡献率为：

其中，Yi(t-1)为t-1年第i省份种植业总产出，Mi(t-1)为t-1年第i省份农业机械总动力，ΔYit为t年第i省份种植业总产出与t-1年数值之差，ΔMit为t年第i省份农业机械总动力与t-1年数值之差。若要计算一段时间的贡献率，则将t-1中的1改为这一段时间的总年数，如计算1979—2018年这一段时间累计的贡献率，则t=2018，1改为39即算得1979—2018年累计的农业机械化贡献率。其他要素贡献率计算方法同。

1.3 变量选择与计算方法

根据以往研究，选取下列指标作为模型变量。

1）种植业总产出（Y）：设置种植业总产出为被解释变量，本文种植业产出用农业总产值（不含林业、牧业、渔业）来衡量。为使数据具有可比性，以 1978年为基期，通过农业总产值指数计算农业总产值。

2）资本投入：资本投入通常用物质消耗来表示，但是各省种植业物质消耗的统计数据较少，根据已有的研究以及数据的可得性，本文用化肥施用量（折纯量）（F）、农业机械总动力（M）作为资本投入的量化指标[24]。

其中农业机械总动力为关键解释变量。农机总动力在2016年统计口径发生调整，农用运输车不再作为农业机械纳入统计范围，为保证数据内涵同一，对2016、2017和2018年农机总动力做了修正，MTR表示农用运输车动力。MF表示未统计农用运输车动力的农机总动力。

3）劳动力投入（L）：各省种植业劳动力投入用各省第一产业从业人员表示，部分省份统计数据存在缺失，需进行处理：上海市2018年第一产业从业人员数据缺失，用趋势递推法进行处理；黑龙江省在2011—2013年第一产业从业人员数据存在缺失，使用线性插值法进行处理。其他省份、年份缺失值用上述同样方法处理[25]。

4）土地投入（D）：土地投入指标用农作物播种面积（DA）表示。土地投入还要考虑受气候条件以及其他资源的影响导致的质量差异[26]，因此本文考虑用有效灌溉面积（IA）、成灾面积（CA）对农作物播种面积加权。成灾面积的20%左右为绝产，因此播种面积要扣掉成灾面积的20%；同时考虑有效灌溉的土地产量要高于不具备灌溉条件的土地，因此给与1∶1的权重将有效灌溉重复计算一次，则土地投入（D）计算方法为：

1.4 模型选择

面板数据的处理方法一般有混合模型、固定效应模型和随机效应模型。根据似然比检验，固定效应模型比混合模型效果更好，且常数为索洛余值，显然不是随机数，故选用固定效应模型对数据进行回归，测算各生产要素的生产弹性。

固定效应模型根据其系数的变化有可分为变截距固定效应模型与变系数固定效应模型，即截距与系数可随个体或时点变化。本文研究时间跨度较长，技术进步率在这段时间内可能发生较大变化，各省之间个体差异较大，采用变截距、变系数固定效应模型是可行的。根据索洛余值是否随时点变化、土地投入是否随个体变系数、农机总动力是否随个体、时点变系数，建立模型。

通过似然比检验得：索洛余值随时点变、土地投入个体变系数、农机投入个体变系数的固定效应模型，更适合用于省际面板数据测算中国种植业贡献率。也即是，全要素生产率随着时间变化而进步，而非定值；同时，土地和农机两种要素的产出率在各省之间存在较大差异。

1.5 数据来源

本文数据来源为历年各省统计年鉴、《中国统计年鉴》《新中国60年统计资料汇编》《新中国农业60年统计资料》《中国农业机械工业年鉴》和国家统计局网站收集28个省份（西藏自治区统计数据不全，港澳台地区数据口径不统一，舍去。1988 —2018年海南省数据归入广东省， 1997—2018年重庆市数据归入四川省计算，以保证截面数据前后一致）。通过各渠道数据整理，获得了1979—2018年模型需要的全国及各省农业总产出、农机总动力、第一产业从业人员、化肥施用量、耕地面积、有效灌溉面积、主要农作物播种面积、成灾面积等指标的面板数据。

表1为相关省级数据的描述性统计。

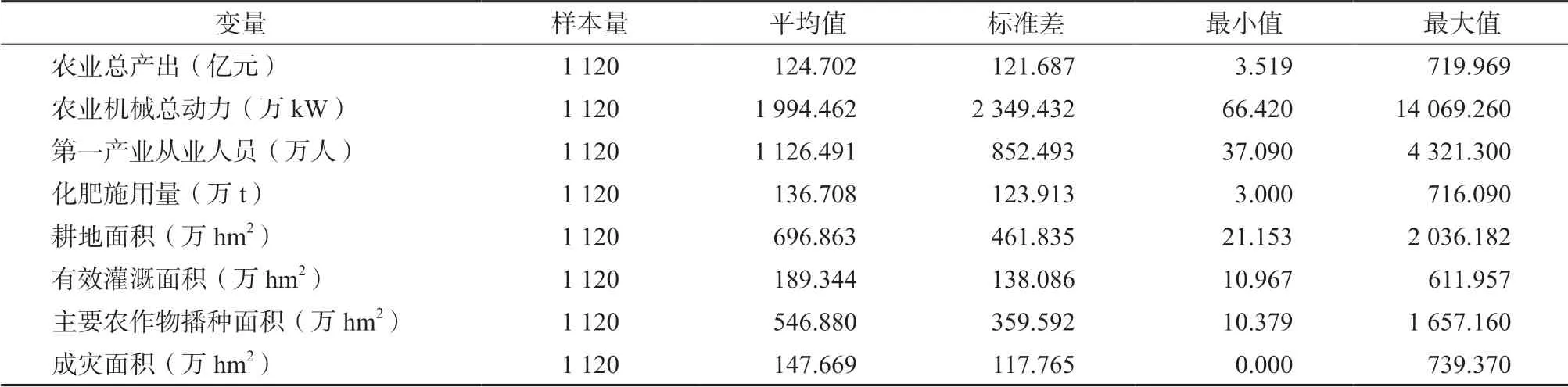
表1 相关数据描述性统计Table 1 Descriptive statistics

2 结果与分析

2.1 农业机械化发展状况分析

1979—2018年农作物耕种收综合机械化水平与种植业总产值总体均为上升趋势（图1）。1978年以安徽小岗村“大包干”为序幕的农村改革开始后，农村迅速实行了家庭联产承包制，从集体公社大面积共同作业转化为家庭联产承包的小规模作业，1984年年底，包产到户的生产责任制基本普及开来[27]。农户家庭联产承包责任制规模细小，土地零碎，原有的大型农机还没有适应经营规模的变化，1979—1985年耕种收综合机械化率稍有下降，而家庭联产承包责任制解放和发展了生产力，破除高度集中的计划管理体制的束缚，在这期间种植业总产值保持上涨。1985年随着农业机械逐渐适应小规模作业状况，农机社会化服务、跨区服务体系兴起，耕种收综合机械化率停止下降[28]。而同时农村非农产业发展，农民有更多的就业选择，农业生产产量不稳定，收益率较低，农业机械投资较大，退出农业经营的农户逐渐增多，在这一阶段农业机械化的发展主要依靠小型农机，耕种收综合机械化水平增长缓慢[29]。随着国家对农业的重视以及对农业机械补贴力度的增大，2004年以后耕种收综合机械化水平加速上升。

1980—2018年全国种植业总产值增长率与农业机械总动率增长率关系见图2，可以看出：1980—1985年期间，种植业总产值增长率较大，最高达到11.5%，显然土地分包到户极大释放了农户的生产热情，劳动生产率和土地产出率都出现了大幅度提升导致种植业总产值快速增长。但在1985开始出现了增速放缓并趋于4%上下波动的情况。农业机械总动力增长率在1990年之前整体处于下降趋势，农机发展呈现低迷状态，增长率最低曾经仅为2.28%。但之后开始恢复，到1997年最高达9%，后面开始下降但也维持在5%左右波动。整体来看，农业机械总动力增长率和种植业总产值增长率之间呈现出一定相关性，比如1991—1995年期间，农业机械总动力增长率呈上升趋势，而种植业总产值增长率趋势相同；1996—2003年之间农业机械总动力增长率整体呈下降趋势，同期种植业总产值增长率也呈下降趋势。当然，是否真的有显著关联，还需要在下一节内容中进行进一步的定量研究。

2.2 各省平均贡献率分析

运用stata15软件对模型进行估计，面板数据存在异方差和自相关，所以这里使用聚类稳健标准误修正后的t值。拟合优度为0.99，拟合效果较好。再根据公式（3），算得农业机械化对各地区种植业的贡献率，结果见表2。

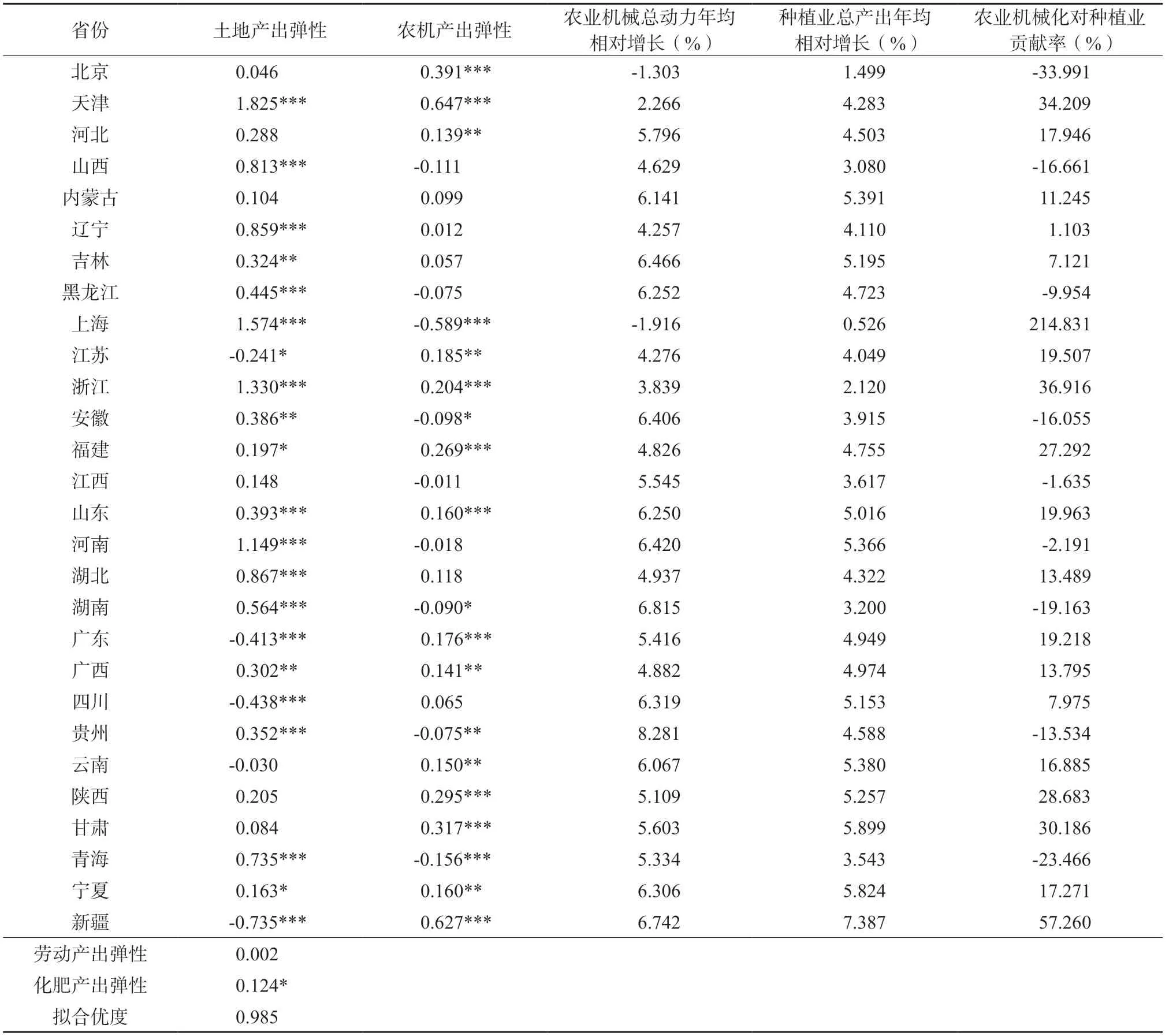
表2 1979—2018年系数估计量及农机化贡献率Table 2 Coefficient estimation and agricultural mechanization contribution rates in 1979-2018

从关键解释变量农机贡献率看，1979—2018年间农业机械化在中国大部分地区的农业生产中发挥着较大的作用，继续增加农业机械的投入仍旧可以推动种植业的发展。其中，贡献率超过30%的有天津、上海、浙江、甘肃和新疆。特别是新疆，农业机械总动力对种植业总产值的弹性系数为0.63，贡献率为57.26%。贵州、湖南和青海等省份农机总动力对种植业总产值的影响均在10%水平下显著为负，可能原因是贵州、湖南和青海等省耕地中丘陵山区占比较高的省份由于地貌限制，无法使用大中型农机作业而只能使用微耕机等小型农业机械，而这些机械的效率远远低于大中型农业机械，因此存在投入增速高但对应产出增速水平却偏低，使得弹性为负。此外，还看到安徽和上海等平原省份贡献率也为负，表明这些省份存在这可能存在农机保有量过剩的情况，但考虑到跨区作业的溢出效益[30]，并不能直接证明这些农机在全国范围内就一定算过剩的。

从土地投入的弹性看，由于1979—2018年各省土地投入面积变动不大或有减少，同时其他如种子、化肥等土地替代性要素的广泛使用使得土地产出率不断提升，低产土地即使大幅度退出亦不会影响种植业产出，导致土地资源变动对种植业的影响相对较小，甚至个别省份弹性为负（此处涉及另一问题，“占补平衡”的严格土地政策，是否让各省将优质耕地转化为建设用地而用劣质的荒地复垦，进而导致了这一现象？本处不做深入讨论）。天津、浙江、上海和河南土地投入对种植业总产值的弹性系数大于1，即土地投入增加1%则种植业总产出增加1%以上，土地资源在这些地区尤为重要。可能解释是，这些省市优质的水浇地占比和增速较高。

从劳动投入要素看，第一产业从业人员对种植业产出弹性为0.002，在10%水平下不显著（表2），表明第一产业从业人员对种植业的影响很小。其原因在于，农业劳动力虽然在大幅度下降，但替代农业劳动力的农业机械也在快速增长，所以表现为农业劳动力下降对农业产出的影响并不显著。若参照美国等主要农业出口国的劳动生产效率，我国农业劳动力还有非常大的下降空间。

从化肥投入要素看，化肥施用量对种植业产出弹性为0.124，在10%水平下显著（表2），对种植业总产值有着正向的影响，化肥施用量每增加1%，种植业总产值增加0.12%，化肥在1979—2018年之间，对种植业总产值有明显的正向推动作用。

图3为模型计算得到的1979—2018年每年的综合技术水平，代表了该年种植业总产值增长中不能归因于模型中其他生产要素的增长的部分，包括劳动力素质、引进先进技术等。1979—2018年间，综合技术水平逐年增长，增长了近3倍，表明产出增长中，由技术进步带来的增长不断上升。

2.3 全国农业机械化贡献率分析

全国历年农业机械化贡献率的计算有两种方式：第一种是运用表2分省计算的农机产出弹性数据，根据公式（4）进行加总计算得到全国历年农机化贡献率（图4：分省加总）。但如前述模型结果分析中提到那样，由于未考虑跨区作业的溢出效应，因此计算出的各省农机装备贡献率可能有所误差。因此，本研究同时采用了第二种方法，即直接运用全国年度数据，在控制随时间变化的技术进步基础上，运用C-D生产函数进行估计各要素的产出弹性（表3）并按照公式（3）计算出全国农机化贡献率（图4：全国数据计算）。图4展示了两种方法计算出的1979—2018年分年度的全国农业机械化贡献率结果。加上技术进步贡献率，各要素贡献率之和应当为100%，用一个固定弹性估计所有时期的贡献率，存在一定误差，故将总贡献率超过200%的年份结果视为异常值，1980年分省加总结果与1980年、1985年、1988年和1991年全国数据计算结果在图4中不再展示。1986年种植业总产值增长率为负。根据贡献率公式可知：如果处于分母位置的产出增长率为负，那么处于分子位置的两项因子：投入要素的产出弹性为正、要素增长率即使为正，得出来的贡献率也一定是负的。一般认为种植业总产值增长率为负时，计算出的贡献率无效，因此对1986年结果不做展示。

从图4可以看出：1）无论是分省加总结果还是全国数据计算结果，整体趋势是一致的。全国数据回归结果波动较大，所有年份贡献率均大于分省加总结果，是由于在分省计算时，未考虑跨区作业的溢出效应，因此低估了各省农机装备的贡献率。2）1979—2018年农机贡献率总体表现为先增后减，今后应注重农业机械化的效率，对动力机械、谷物收获机械等存在保有量过剩的农业机械降低补贴额度，并鼓励社会化服务。

与1979年相比，2018年累计的农业机械贡献率是多少？表4分别展示了分省加总和全国数据计算得到的各投入要素累计贡献率。可以看出，与1979年相比，无论是哪种方法计算出的结果，都表明农机是贡献最大的要素。由于分省加总结果未考虑跨区作业的溢出效应，因此我们采用全国合计数据计算结果，即与1979年相比，2018年的种植业产出增加部分农机贡献了其中54.196%。换句话说，如果没有农业机械化，在保持1979年的劳动生产率条件下，2018年的种植业产出将下降54.196%。

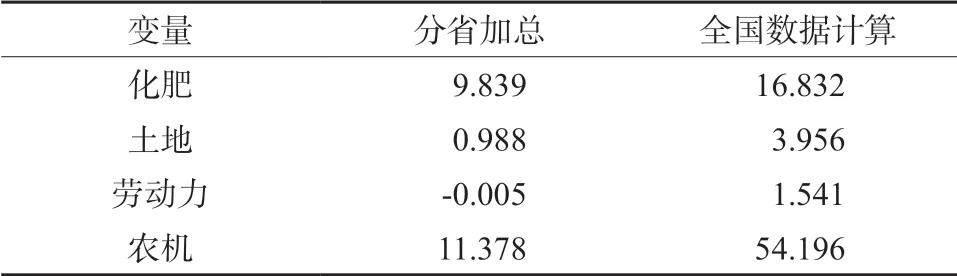
表4 1979—2018年各投入要素对中国种植业增长的 累计贡献率（%）Table 4 Cumulative contribution rates of input factors to the growth of China’s crop industry between 1978 and 2018

3 结论与建议

3.1 结论

研究表明，1979—2018年耕种收综合机械化水平与种植业总产值总体均为上升趋势。农业机械化对种植业产值具有较高的贡献率，分省面板数据表明绝大部分省份农业机械对种植业产值的贡献率都是正的。同时，分省加总计算出的农机贡献率和用全国数据回归计算出的农机贡献率，除了1986年消除物价指数的种植业总产值负增长导致农机贡献率为负数以外，其他年份都是正的，且所有要素中无论哪种算法农机的贡献率都远高于化肥、劳动力和土地等其他要素。

但注意到，近年来农业机械化对种植业总产值的贡献率不断降低，农机总动力增加对种植业总产值增加的贡献在降低。现阶段平原地区耕、种、收阶段机械化已经到达较高水平，但丘陵地区的农业机械化发展受到地形等多因素的限制，丘陵山区县农作物综合机械化水平远低于全国平均水平。丘陵地区农业机械化发展具有较大的潜力。农业机械化在经济作物、林果业、畜禽养殖、水产养殖和设施农业等领域还有诸多不足，未来应当更加重视农业机械化在这些领域的发展，推动农业全程、全面机械化。

3.2 建议

1）继续加大农业机械化支持力度，丰富支持政策。中国农业要参与国际竞争、要保障农产品供给安全，那么必然要依靠农业机械化，传统的生产方式支撑不起农业农村现代化。目前农业机械化支持政策过于单一，主要依靠购机补贴政策，而欧美、日韩等国家和地区的燃油补贴或退税政策、贷款贴息政策等组合政策，我们应借鉴和丰富农业机械化支持政策。

2）提高农业机械化效率，补短板强弱项。当前拖拉机、谷物收割机等传统农业机械处于过剩状态，而经济作物、林果业、畜禽养殖、水产养殖、设施农业等领域和丘陵山区农业机械化水平还较低，因此应将主要资源向薄弱领域和地区倾斜，降低保有量过剩的农机支持力度。

3）加强农田和机耕道等基础设施建设，促进丘陵山区农业机械化的发展。我国丘陵地区耕地面积、播种面积均占全国三成左右，但由于农田分散、零碎、不平整、缺乏机耕道等原因不适合使用大中型机械，极大的限制了丘陵地区的劳动生产率。应大力推动以地块“小并大、短并长、坡改平、弯改顺、互联互通”为主要内容的农田宜机化改造工作，为农业机械作业提供基础条件。