用问题提升素养 以引导发展能力——“同角三角函数关系式”课堂实录与反思

张炳峰 钱建良 (江苏省宜兴市和桥高级中学 214211)

古人云：“授人以鱼不如授人以渔．”学生解决数学问题能力的提升依赖于对其数学学科核心素养以及数学探究能力的培养．而这两者的培养都离不开教师科学、合理的引导与启发．概念课的教学正是做好“引导与启发”的关键环节．如果教师能让学生充分感知到新知识的由来、生成与发展，那么学生在能力上就能得到升华，数学核心素养的培养与探究能力的提升就能真正落到实处．

2020年12月2日笔者受邀参加了宜兴市丁蜀高级中学开展的“钱建良名师工作室走进丁蜀高中”的活动，并开设了一节题为“同角三角函数的基本关系”展示课，得到了同行的肯定与好评．笔者在磨课、授课后，从各位观课老师的评议中深受启发，现将这堂课的课堂实录与反思整理如下．

1 创设情境——激发问题意识

师：时光荏苒，岁月如梭，一转眼我们都已经是高一的学生了，那么大家对自己上幼儿园还有印象吗？

生：有(没有)．

师：有些同学有印象，有些同学没印象，那大家读幼儿园时，对幼儿园的什么玩具器材最有印象呢？

生：滑滑梯，跷跷板，荡秋千……

师：那老师今天就有一个问题与滑滑梯有关：

图1

师：很好！通过联立方程组解决问题．本题是否还有其他方法呢？(分析)已知斜边AC，要求直角边BC，最好是知道角θ的哪个三角函数值？

生：sinθ．

师：那已知tanθ，能否求出sinθ呢？他们之间是否有关系呢？

师：大家都听过一句话：南美洲亚马逊河雨林中的一只蝴蝶，偶尔扇动几下翅膀，可能引起两周后美国德克萨斯州的一场龙卷风．这就是著名的“蝴蝶效应”，其本意是说事物初始条件的微弱变化可能引起结果的巨大变化，两个看似毫不相干的事物，却会有着千丝万缕的联系，那么“同一个角”的三角函数也一定会有非常密切的联系！到底是什么关系呢？这就是本节课所研究的问题：同角三角函数关系式．

设计意图新的课程理念给我们指明：数学源于生活，又服务于生活．新课改也正全力构建生活化的课程结构，数学课堂更应该如此．若能将融科学性、趣味性、探究性和发展性为一体的问题情境设计成导入环节，则学生的求知欲将会更浓厚，对数学学习的热情也将更高．

2 归纳猜想——促发探知欲望

师：在探究本节课的问题之前，我们一起来完成下面的问题.

问题2写出下列角的三角函数值，观察其间的关系并猜想之间的联系．

sin αcos αtan αsin2 α+cos2 αsin αcos α30°45°60°

生：探究发现，① sin230°+cos230°=1,sin245°+cos245°=1,sin260°+cos260°=1；

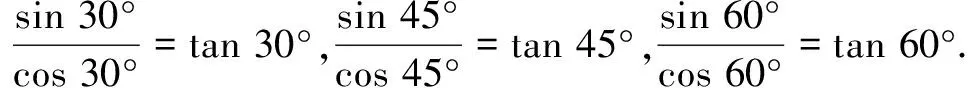
问题3从以上结果中，你能发现什么一般规律？你能否用代数式表示这两个规律？

师：非常好！那么，这个规律是对问题2中的锐角成立，还是对任意角均成立呢？能否证明？

设计意图运用深度学习的理论，通过创设学生主动探究问题的情境，再鼓励学生从特殊到一般，归纳猜想同角三角函数的基本关系，进而发展与提升学生的数学抽象素养．

3 猜想证明——活化数学思维

师：证明之前，我们复习一下书本中任意角三角函数的定义(图2)．

图2

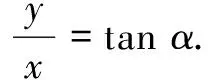
师：下面，请同学们分小组讨论完成证明．(分小组讨论)

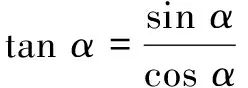
设计意图运用最近发展区理论，启迪学生要关注新旧知识之间的各种关联性，探究旧知如何生成新知，并在已有知识体系中纳入所学知识，使得学生的数学认知结构能够不断地得到优化与提升，从而发展学生的逻辑推理素养．

4 完善自我——严谨数学思维

问题4那这两个公式是对任意角均成立吗？是否有限制条件呢？

(学生小组讨论)

师：同角三角函数的基本关系总结如下：①平方关系：sin2α+cos2α=1，②商数关系：tanα=

设计意图严谨性是数学学科的基本特点，数学结论的叙述必须精炼、准确．该环节的设计主要是想让学生透过分组讨论与合作交流来挖掘限制条件，感受数学的严谨，也更想让学生体会无限与有限、变与不变在数学学科中所呈现出的那层唯美辩证关系，充分感受数学之美．

5 公式运用——升华数学素养

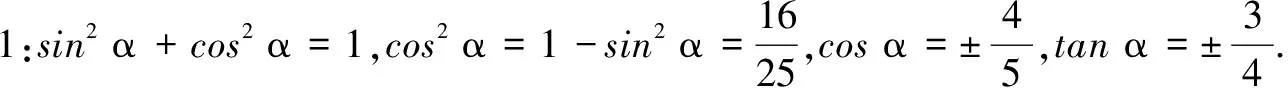
师：哪位同学有不同意见？

师：那应该有几种对应？为何？

师：非常好！那本题该如何书写？

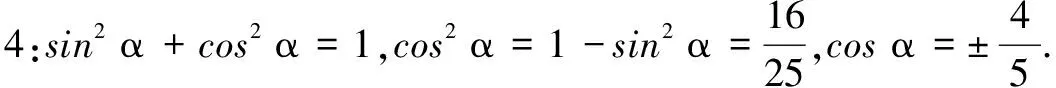
师：很好！解决本题时，我们要时刻关注 sinα,cosα,tanα三者之间的符号问题，要学会分类讨论．

设计意图设计问题5的目的是深化学生对新知的理解与运用．本题紧紧围绕同角三角函数基本关系，以方程思想为核心，真正用意在于从方程角度解释同角三角函数基本关系，帮助学生明确“知一求二”的基本手段，同时渗透分类讨论的基本思想在数学解题中的运用，培养学生的数学运算素养．

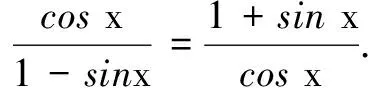
师：这位同学采用作差的方法，通分后利用等式变形cos2x=1-sin2x完成证明.还有其他方法吗？

师：很好！但是否有些条件需要讲清楚呢？

生3：上下同乘以1+sinx，最后又约去 cosx，需要说明由题知1+sinx≠0，cosx≠0．

师：这位同学思维很清晰，数学解题必须要严谨．

师：请同学们找出本题三种解法的本质．

生：主要抓住公式sin2α+cos2α=1的变形运用．

设计意图问题6的设计充分抓住“1”的不变性，从证明手段的三种角度诠释该题，用意主要有三点：(1)深层次、多维度地运用公式，帮助学生灵活掌握公式；(2)旨在让学生感受数学的解题手段是多面的，更多的是需要寻找数学问题和方法中的本质属性，这样难题才能迎刃而解，最终培养学生的逻辑推理和数学运算素养；(3)为下一环节“发挥想象”埋下伏笔．

6 发挥想象——激发数学兴趣

问题7同学们能根据本题，自己当回老师，出题给其他同学做吗？分小组讨论．

(小组讨论出两组题目，并分别请学生上黑板板演)

生1：求证：sin4α+cos2αsin2α+cos2α=1．

(投影)生2：左边=sin2α(sin2α+cos2α)+ cos2α=sin2α+cos2α=1=右边．

师：有不同看法吗？

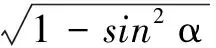
师：很好！那能不能对这题改进一下？

生：加个条件，α在第一、四象限．

师：那不加条件是否可以呢？如何操作？

生：可以，运用分类讨论思想．

师：感兴趣的同学请在下课后完成解答，我们再一起探讨！

设计意图学生是课堂的主体，让学生参与编题、做题、评题，这样不仅能让学生从教师的角度思考所学内容，而且更有利于学生开展深度学习，对知识与知识之间的内在联系也将体会得更深刻，知识的内化效果更理想，学习成功的体验更丰富．

7 归纳总结——建构知识体系

师：通过本堂课的学习，你有哪些收获或疑问？

生1：学到了同角三角函数关系式．

师：这是知识点，那你还有学到哪些数学思想吗？

生2：在遇到符号问题时要学会分类讨论．

师：通过本节课的学习，你对以后的数学学习有哪些体会？

生3：我对数学更有兴趣了，也有点理解了数学源于生活，另外，学习数学需要严谨的态度！

8 反思

著名教育家叶圣陶说过：“凡为教者必期于达到不须教”“教是手段，不须教是目标，达到是过程．”如何达到不须教？作为教师，就应该注重培养学生的数学学科核心素养以及数学探究能力．新课标指出：“高中数学课程应提高学生的思维能力．”如何有效培养学生的核心素养和探究能力？教师在设计教学环节时应充分考虑学生的立场、学生的数学认知水平等问题．好的教学能充分激发学生的求知欲望．如本节课的第一个环节“创设情境—激发问题意识”以及第六个环节“发挥想象—激发数学兴趣”，在磨课环节有教师提出不同意见，认为这两个环节可能会浪费本节课的整体时间，导致完成不了教学任务，但笔者认为正是这两个环节值得教师去“浪费时间”．因为兴趣是学习的动力，是学习的源泉，学生只有对数学感兴趣，才愿意去想、去学，如此，才谈得上培养核心素养．

高中数学新课标提出了发现问题、提出问题、分析问题和解决问题的能力，如何能发现、提出问题？这需要教师科学、合理地引导与启发，这种引导与启发不是高谈阔论，而是要结合学生的最近发展区，让他们产生“跳一跳，也许我能摘得到”的感觉．如在本节课的第三环节“猜想证明—活化数学思维”中，笔者在最初上课时，没有提供复习三角函数定义这一环节，这引起听课教师的质疑，学生是否有能力想到从定义角度证明同角三角函数关系式？直接要学生证明，是否已经跳出了学生的最近发展区？最终笔者听取了意见，保证了上课的效果是满意的，学生的收获也是充实的．在第四环节“完善自我—严谨数学思维”中，笔者初始上课时直接投影同角三角函数关系式的限制条件，被建议第三环节已经复习了三角函数的定义，而限制条件也是基于定义找到的，可否尝试让学生自己得出限制条件呢？于是笔者也听取意见，增加了这一环节．

综上，设计科学、合理的引导与启发环节能充分激发学生的灵感火花，也更能让学生主动融入数学的学习.