m法和有限元法对桥梁桩基的计算探讨
高能祥,方 健
[同济大学建筑设计院(集团)有限公司,上海市 200092]
0 引言
桩基是指设置在地面以下一定深度的圆柱状或管状的基础构件,是桥梁等其他各种构筑物中最常用的基础形式。桩基对地质条件广泛适用,基础承载力高,不均匀沉降较小;且当地震发生时,桩基整体破坏的概率小,能够防止构筑物倒塌,减少人员伤亡和财产损失。随着施工机械化和检测技术的发展,桩基的施工速度和施工质量得到大幅提升,桩应用愈加广泛。
在承受水平荷载作用下,桩基的工作原理是桩-土的相互作用问题[1]。此时,桩基依靠桩基周围土的抗力来承担其所受的水平荷载。桩基承受水平力作用下,导致桩基发生水平位移,此时桩基压迫桩周土产生相同方向的变形,迫使桩周土产生反向抵抗力,此反向抗力会阻止桩基位移的继续发展。
1 m 法计算简介
桩基在水平力作用下,最常用的计算方法是地基反力系数法。地基反力系数指的是地基反应模量,即土对桩基产生的反向抗力与土的位移的比值。地基反力系数采用的是Winkler 地基模型[2]。它将桩侧土离散为一个个相互独立的弹簧,且弹簧所产生的抗力与其发生的位移成正比例关系。

式中:p 为桩基所承受的单位压力;Cz为地基反力系数;yz为相应的土体位移。
根据式(1)建立Winkler 弹性地基梁模型如下:
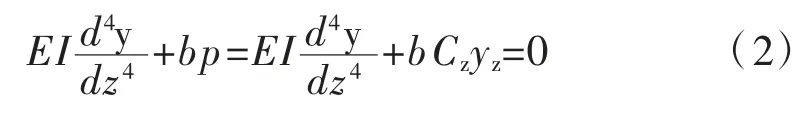
式中:EI 为桩基抗弯刚度;y 为桩基轴线挠曲位移;z为桩基对应深度;b 为桩基计算宽度。
根据地基反力系数Cz沿桩基深度不同的分布图示,形成了Cz不同的几种求解方法。

式中:k 比例系数;n 为指数。
如图1(b)所示,n=0 时,Cz=k,此方法被称为张(有龄)氏法。该方法认为地基反力系数为常数,不随桩的深度变化。
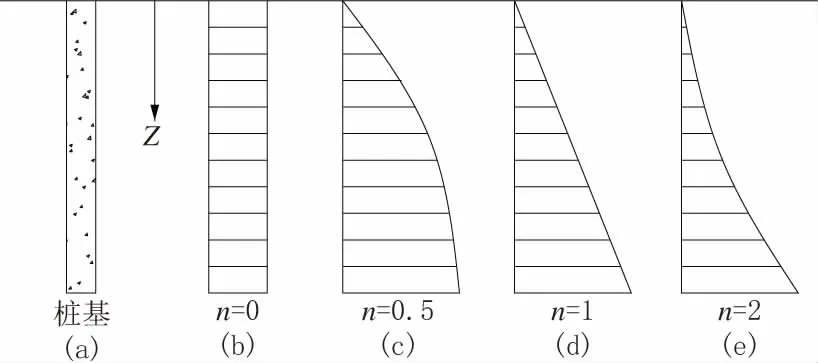
图1 地基反力系数沿桩基深度的分布图示
如图1(c)所示,n=0.5 时,Cz=kz0.5,此方法被称为C 法。该方法认为地基反力系数沿桩的深度成凸形抛物线变化。
如图1(d)所示,n=1.0 时,Cz=kz,此方法被称为m 法。该方法认为地基反力系数沿桩的深度成线性变化,令k=m,则Cz=mz。
如图1(e)所示,n=2.0 时,Cz=kz2,此方法被称为k 法。该方法认为地基反力系数沿桩的深度成凹形抛物线变化。此方法由于计算出的桩身弯矩结果比实际偏大较多,故较少采用。
上述中的m 法是我国计算桩基在水平荷载作用下的常用方法,也是《公路桥涵地基与基础设计规范》(JTG 3363—2019)[3]中计算桩基的水平位移和作用效应的指导方法。根据Cz=mz,重新建立Winkler弹性地基梁模型公式如下:
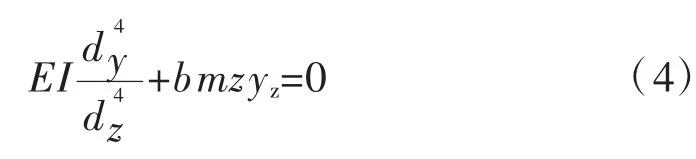
式中:m 为地基反力系数的比例系数;z 为桩基对应深度。
上述公式可写为:
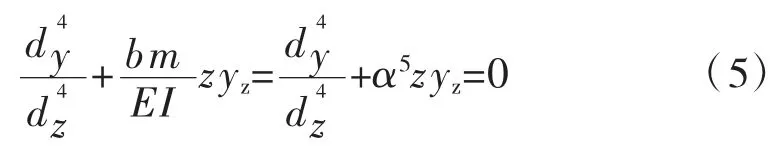
式中:α 为桩基的变形系数,其值为:

当桩基桩头承受水平推力H0和水平弯矩M0的情况下,根据式(5)可推导出弹性桩的内力和位移公式,如下:
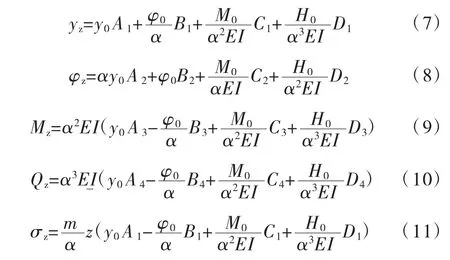
式中:yz为桩的水平变形位移;φz为桩的转角位移;Mz为桩截面的弯矩;Qz为桩截面的剪力;σz为桩周围的土压力;A、B、C、D 为无量纲系数,可通过查询《公路桥涵地基与基础设计规范》(JTG 3363—2019)[3]表L.0.8 取用。
2 桩基有限元法模拟简介
有限元分析是目前结构设计计算的常用方法。它利用结构材料本身的本构关系和结构自身的边界条件建立结构受力与位移的变形协调方程[4],求解结构的内力和位移。有限元分析同样适用于桩基计算分析,采用弹性地基梁理论建立桩基有限元模型,将桩基用梁单元模拟,采用土弹簧模拟土对桩基的约束作用。在桩基的有限元建模中,需遵循如下假设条件:
(1)将土体视为线弹性体,土弹簧刚度随深度线性增加。
(2)同一深度的弹簧刚度为定值,不随桩基位移变化[5]。
(3)忽略土体对桩基的摩擦力和黏结力等作用。
根据以上假设,土弹簧刚度计算公式如下:

式中:Kz为深度z 处的土弹簧刚度;b 为桩基计算宽度;m 为地基反力比例系数;hz为深度z 处的土层厚度。
3 算例简介
本文采用两个算例进行分析对比,分别为单桩模型和群桩模型。算例简介如下:
3.1 算例一
算例一为单桩模型,如图2 所示。采用桩径为1.0 m 的摩擦钻孔灌注桩基,桩长20 m。桩端处土性为可塑性黏土,取地基反力系数m=5 000 kN/m4。桩基的计算宽度b 按《公路桥涵地基与基础设计规范》(JTG 3363—2019)[3]L.0.1 条计算。经计算,b=1.8 m。则由式(12)可计算出桩基各深度处的土弹簧刚度。
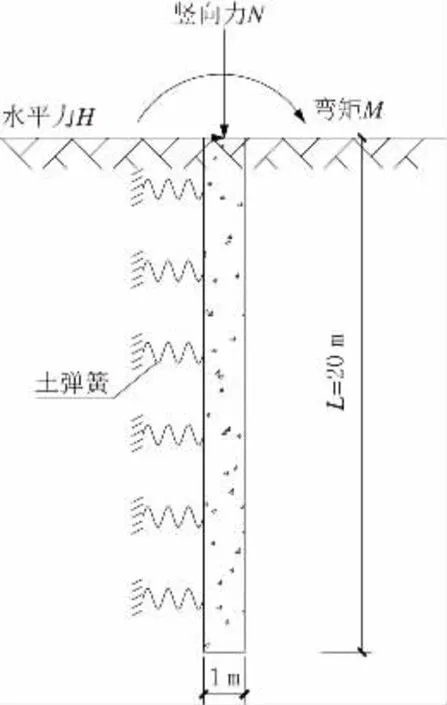
图2 算例一单桩模型图示
桩顶施加竖向力N、水平力H 和弯矩M,分别为N=1 000 kN,H=500 kN,M=1 000 kN·m。其中,弯矩与水平力产生的位移效应同向。
3.2 算例二
算例二为群桩模型,如图3 所示。承台为2 m高,承台下设置12 根桩径为1.2 m 的摩擦钻孔灌注桩基,桩间距均取3.0 m,桩长20 m。桩端处土性为可塑性黏土,取地基反力系数m=5 000 kN/m4。桩基的计算宽度b 按《公路桥涵地基与基础设计规范》(JTG 3363—2019)[3]L.0.1 条计算。经计算,b=1.386 m。则由式(12)可计算出桩基各深度处的土弹簧刚度。

图3 算例二群桩模型桩基平面(单位:cm)
在承台中心施加竖向力N、水平力H 和弯矩M,分别为N=20 000 kN,H=1 000 kN,M=10 000 kN·m。其中,弯矩与水平力产生的位移效应同向。
4 算例结果对比
采用上节的两个算例进行分析对比,分别采用m 法和Midas Civil 有限元模型计算桩身的各反应结果,包括桩基水平位移、桩身弯矩、桩身剪力和桩周土应力。
4.1 算例一
单桩模型采用m 法计算的桩身各反应结果见表1。
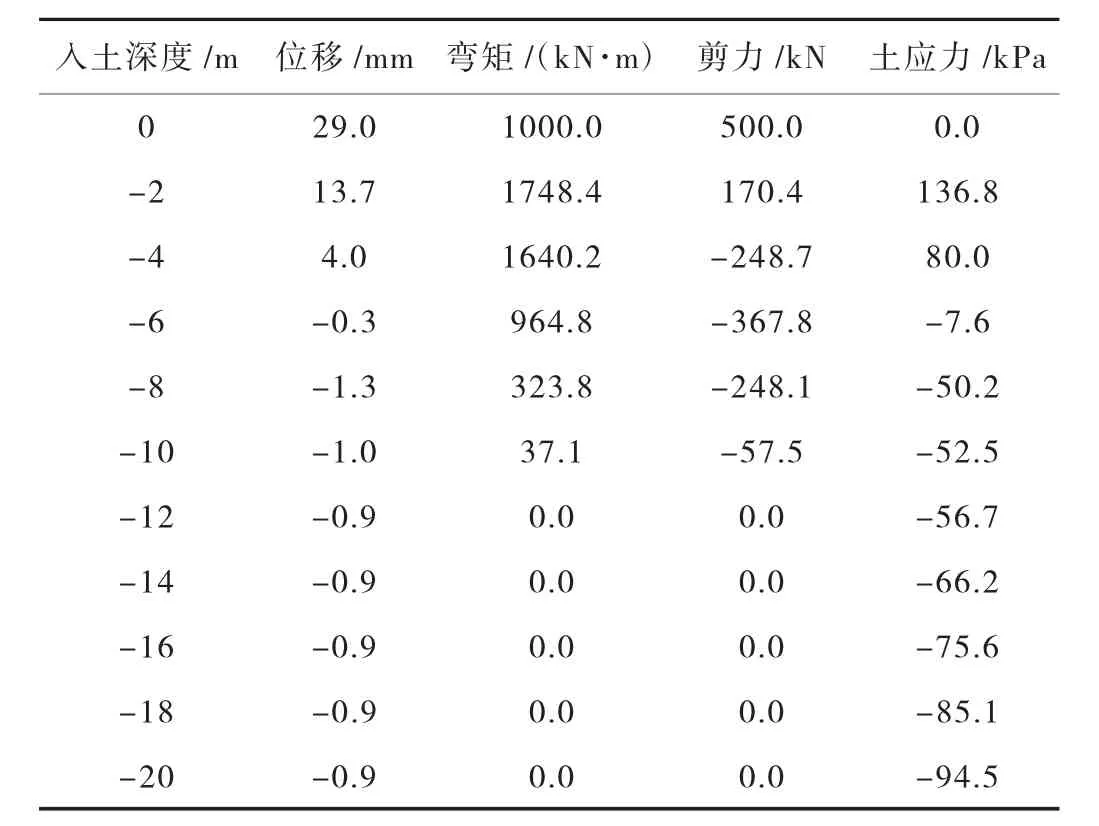
表1 单桩模型m 法计算结果
单桩模型采用有限元法计算的桩身各反应结果见表2。
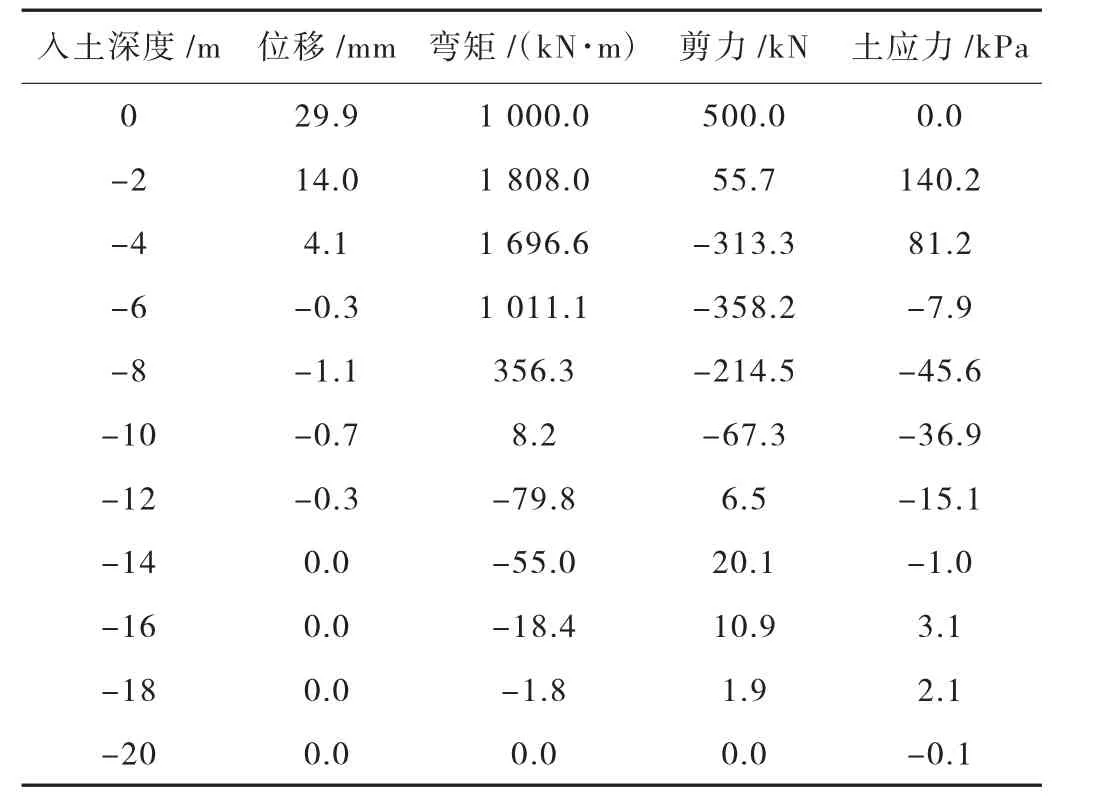
表2 单桩模型有限元法计算结果
单桩模型采用m 法和有限元法计算的桩身各反应结果对比如图4~图7 所示,最大值差距见表3。

表3 单桩模型桩身结果差距分析
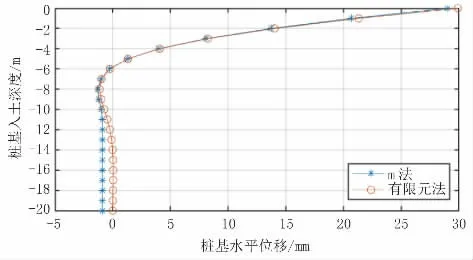
图4 单桩模型桩基位移结果对比(单位:mm)
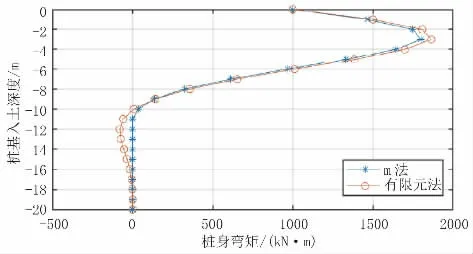
图5 单桩模型桩身弯矩结果对比(单位:kN·m)
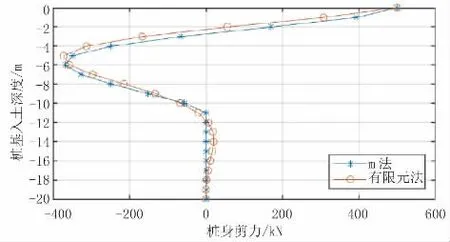
图6 单桩模型桩身剪力结果对比(单位:kN)
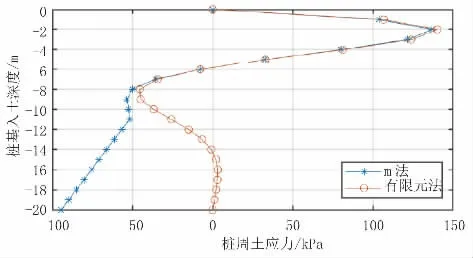
图7 单桩模型桩周土应力结果对比(单位:kP a)
根据以上计算结果,单桩模型中两种方法计算出的桩身各反应结果最大值差距均小于5.0%,且除桩周土应力结果外,其他反应结果趋势较一致。
4.2 算例二
群桩模型采用m 法计算的桩身各反应结果见表4。

表4 群桩模型m 法计算结果
群桩模型采用有限元法计算的桩身各反应结果见表5。
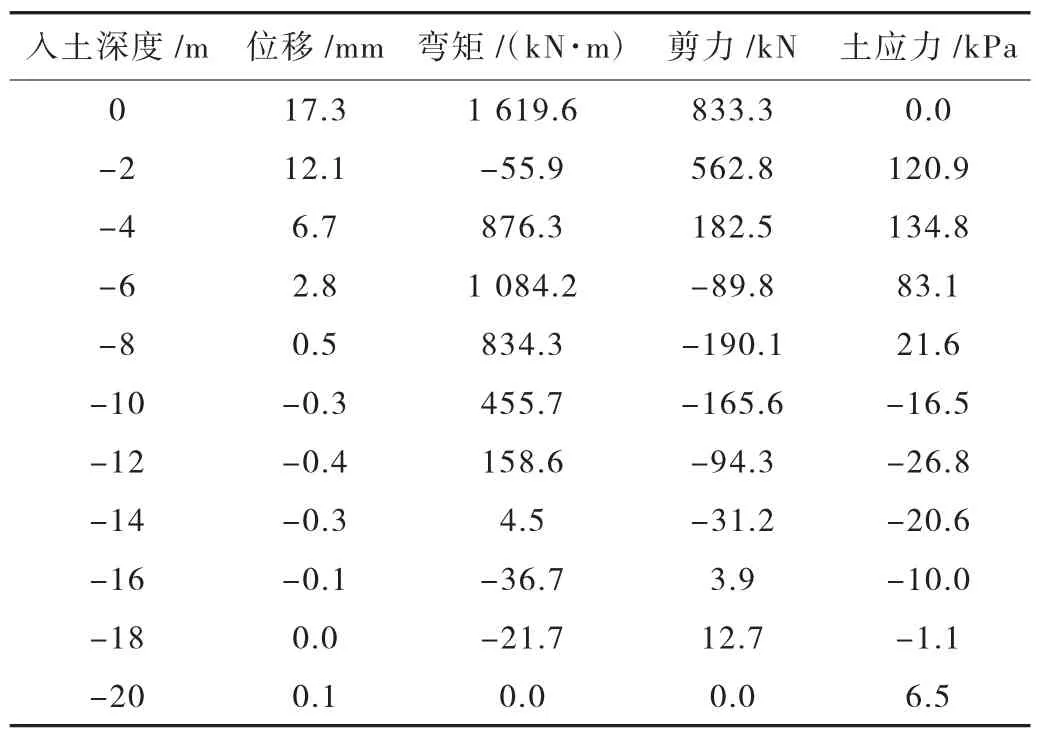
表5 群桩模型有限元法计算结果
群桩模型采用m 法和有限元法计算的桩身各反应结果对比如图8~图11 所示,最大值差距见表6。
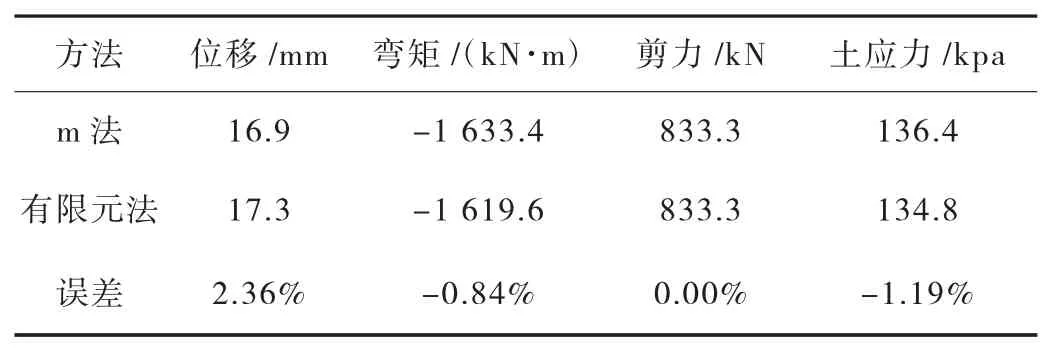
表6 群桩模型桩身结果差距分析
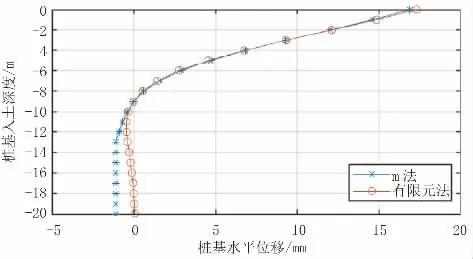
图8 群桩模型桩基位移结果对比(单位:mm)
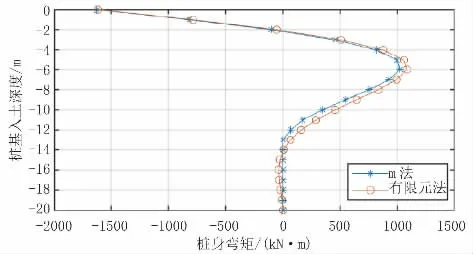
图9 群桩模型桩身弯矩结果对比(单位:kN·m)
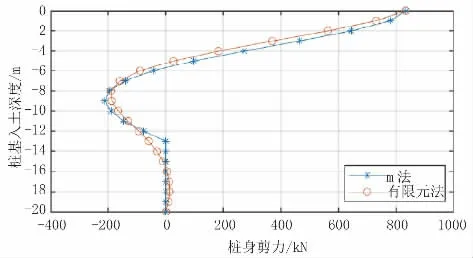
图10 群桩模型桩身剪力结果对比(单位:kN)
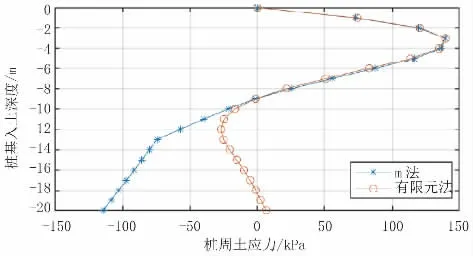
图11 群桩模型桩周土应力结果对比(单位:kP a)
根据以上计算结果,群桩模型中两种方法计算出的桩身各反应结果最大值差距均小于3.0%,且除桩周土应力结果外,其他反应结果趋势较一致。
5 结论
(1)m 法和有限元法在计算的桩身各反应结果差距均较小,且除桩周土应力外,其他反应结果趋势基本一致,说明两种方法计算桩身效应均较准确、可靠。
(2)对于桩基水平位移和桩周土应力两项反应结果,在桩基入土深度较大时,m 法和有限元法计算出的差距较大,且趋势不太一致。这主要是因为m 法在计算过程中未准确计算深度z≥4.0/α(对于单桩模型z≥10.61 m,群桩模型z≥12.94 m)的桩基位移,导致桩基位移计算结果失真;由于桩周土应力σz=mzyz,进而m 法桩周土应力计算结果失真。所以,在桩基深度z≥4.0/α 的桩基位移和桩周土应力计算结果应以有限元法计算为准。
(3)在桩基计算有限元建模过程中,应注意需将桩基梁单元划分较细,一般桩基梁单元长度应小于等于1.0 m 为宜;否则会因为桩头弹簧刚度的模拟不准确导致计算结果与m 法相差较大,导致有限元计算结果失真。

