海底大地基准点圆走航模式定位模型及分析
曾安敏,杨元喜,明 锋,马越原
1.地理信息工程国家重点实验室,陕西 西安 710054;2.西安测绘研究所,陕西 西安 710054;3.信息工程大学,河南 郑州 450001
海底大地基准网是水下导航定位、海底板块运动、海洋环境调查的基础,是海洋地质研究与海底资源勘探的重要支撑[1-3]。美国、加拿大、俄罗斯和日本等发达国家早已开启了海底大地基准网相关研究,并已基本掌握海底大地基准建立与维护技术[4-10]。虽然我国经过几代大地测量工作者的努力,建立了相对完善的陆地大地基准网[11-13],但海底大地基准网建设仍处于起步阶段。
精确测定海底大地基准点坐标是海底大地基准网建设的核心目标。确定海底大地基准点坐标最常用的方法是海面GNSS测量与水声声学测距相结合的方法[4,10]。通过GNSS测量得到载体GNSS天线位置,利用姿态测量数据和GNSS天线到换能器的偏差数据,将GNSS天线位置归算到声学换能器的位置,再利用声学测距数据经处理得到海底大地基准点的位置[14-15]。这种方法测定的海底大地基准点的位置精度主要受GNSS观测误差和声速的不确定性所引起的测距误差的影响[6,16]。利用GNSS事后差分、精密单点定位可获得测量船轨迹厘米级的三维坐标[17],相对于水声声学测距的分米级误差而言,测量船轨迹厘米级误差不是主要误差源。众所周知,水声声学测量中存在声线弯曲和声速变化误差[18],声线弯曲误差与复杂的海洋环境和测量入射角有关[19],声速变化误差与波场、发射和接收换能器之间的距离以及共振频率有关[20]。声线弯曲误差的影响可采用声学信号延迟修正模型来改正,如应用测量区域中的加权声速参数改正[21]、等效声速剖面[22-23]、有效声速模型[24]等可补偿声线弯曲误差,也可通过声线跟踪或自适应分层来进行声线弯曲校正[25-28]。无论是通过测量标定还是模型修正进行补偿,都需要获得测量时间和测量区域内的声速剖面信息,然而声速剖面测量本身具有明显的不确定性和时空变化特性。此外,对声速测距误差可进行参数化建模,将测距误差模型参数与基准点坐标作为待估参数同时解算,通过模型参数吸收测距系统误差的影响[2,29-30]。有学者认为测距系统误差是由水声声速偏差引起的,将声速偏差作为待估参数同位置参数一并解算[11,30],也有学者将每个历元的测距误差作为待估参数,利用半参数平差模型来控制声速变化引起的测距误差的影响[31];如有先验声速或者声线弯曲参数可用,可将它们引入观测模型[32]。考虑到相邻历元的观测环境基本一致,声速测距误差变化也应不大,借鉴GNSS差分思想,可对水声测距时延观测量进行历元间差分,削弱测距系统误差的影响,进而提高海底大地基准点水平位置估计精度[30,33]。由于GNSS测量加水声声学测距的方法仅能在海底大地基准点上方的水面进行观测,因而具有天然的观测不对称性[14,34],以此估计的位置参数的垂直分量的精度往往偏低。为改善基准点垂直分量的精度,有学者提出了顾及波浪影响和深度约束的水下基准点位置确定模型[35-36],附加深度差和水平距离约束的差分定位算法也得以研究[37]。差分算法得以有效应用的前提是相邻路径上的误差基本一致,声线传播路径上的共同误差通过差分得以削弱。观测模式直接决定了海底基准点定位确定的几何观测强度,也是影响基准点坐标精度的一项主要因素。日本学者提出的船痕漂流测量网型[7-8],直线方式[38-39]和圆走航方式[6,11,40]也是测量模式的较好选择。圆走航方式具有近似平面观测对称性,过顶的十字直线走航方式,同样具有良好的观测对称性,均有利于削弱归心参数误差、声速误差、声线弯曲等系统误差的影响[3]。圆走航模式下的差分算法虽然削弱了大部分共同误差的影响,但明显弱化了观测设计矩阵结构。
本文针对圆走航模式下水下大地基准点的定位效能进行系统分析。首先依据声速剖面的变化规律,讨论声学测距非差定位模型和削弱系统误差影响的历元间差分定位模型;然后分析圆走航模式下非差、差分定位模型对参数分量的可估性;从精度最优条件出发,分别推导确保平面位置、深度以及三维位置精度的最佳测量半径;从系统误差角度分析测距系统误差对定位结果的影响;最后利用仿真和深海实测数据验证了定位效能。
1 声学测距观测方程
水声时延测距的观测方程[33]为
ρi,j=f(xi,xj)+δρvd,i+δρvb,i+δρvl,i+δρvs,i+εi,j
(1)
式中,ρi,j表示第i次测量载体换能器与海底应答器j间的水声时延测距观测量;f(xi,xj)表示第i次测量载体换能器与海底应答器j间的直线距离;xi表示第i次测量载体换能器的位置;xj表示海底应答器j的位置;δρvd,i表示海底应答器固有测距误差;δρvb,i表示由背景声速剖面测量不确定性引起的测距误差;δρvl,i表示由潮汐、温度等日变化引起的长周期项测距误差;δρvs,i表示由内波引起的短周期项测距误差;εi,j表示随机误差。
式(1)中系统误差参数δρvd,i、δρvb,i、δρvl,i和δρvs,i的系数均为1。如果没有附加先验信息,这些不同类型的系统误差参数将无法分离,即无法同时解算。通常,采用一个综合性误差来统一表达这些误差参数,即
δρd,i=δρvd,i+δρvb,i+δρvl,i+δρvs,i
(2)
这样,水声时延测距的观测方程可简化为
ρi,j=f(xi,xj)+δρd,i+εi,j
(3)
1.1 非差观测定位模型
水声时延测距观测数据处理中,采用当地水平坐标系ENU有助于分析系统误差对坐标分量的影响,为方便描述,后文均采用当地水平坐标系。其中,n和e分别表示北分量和东分量,u表示天顶分量。
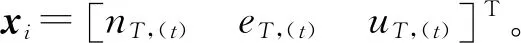
xj=xj,0+dxj
(4)

在xj=xj,0处对式(3)展开,有

δρd+εi,j
(5)

ai,j
(6)
f(xi,xj,0)表示换能器i到应答器j近似位置之间的直线距离,即
f(xi,xj,0)=
(7)
如果预先通过外部校准或经验模型校正了系统误差项,可利用先验系统误差δρd改正实际观测量,则定位模型式(3)的误差方程为
(8)
式中,li,j=ρi,j-f(xi,xj,0)-δρd。
但是在实际应用中,特别是在复杂的海洋环境中,一般无法精确得到系统误差,可将综合系统误差δρd作为待估参数,与海底应答器位置一同估计。式(3)对待估参数xj、δρd,i求偏导,则其误差方程为
(9)
式中,li,j=ρi,j-f(xi,xj,0)。
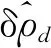
1.2 历元差分观测模型
在复杂的海洋环境中,无法得到精确的系统误差值,建立差分观测方程通常是削弱系统误差影响的一种较合理的方法。通过历元差分可大大减小相邻历元观测模型中的同类系统误差[33]。一般情况下,第i、i+1次测量的时间相近,并且测量母船的位置变化也不大,前后历元的水声测距的各项系统误差也基本相同,即有
(10)
前后历元的综合性系统误差也基本相等,则近似有
δρd,i≈δρd,i+1
(11)
借鉴GNSS差分思想,对水声测距误差方程进行历元差分[33],则式(1)组成的单差观测方程为
Δρi,j=ρi+1,j-ρi,j=(f(xi+1,xj)-f(xi,xj))+
(εi+1,j-εi,j)
(12)
类似前述推导,历元间差分误差方程可整理为
Δvi,j=Δai,jdxj-Δli,j
(13)
式中
(14)
Δli+1,j=(ρi+1,j-f(xi+1,xj,0)-δρd,i+1)-
(ρi,j-f(xi,xj,0)-δρd,i)≈
(ρi+1,j-f(xi+1,xj,0))-(ρi,j-
f(xi,xj,0))
(15)
显然,前后历元的系统误差项δρd,i、δρd,i+1大部分值被差分消除了,系统误差对参数估计的影响得到显著减弱。同时,由于连续两次测量时间非常接近,声学换能器的位置变化小,会有ai+1,j≈ai,j,即历元差分后Δai,j≈0,如此可能会导致式(13)的设计矩阵病态。特别是圆走航时,前后历元声学换能器的垂直分量小,差分后设计矩阵Δai,j的u分量几乎被差掉了,会导致u分量不可估。
将每个观测历元的综合系统误差δρd作为待估参数,非差误差方程式(9)进行历元间差分,其误差方程为
(16)

(17)
可以看出,差分后误差方程式(16)、式(17)的设计矩阵病态。同样,综合系统误差的设计矩阵系数近似为零,系统误差参数也不可估,即式(16)、式(17)无法解出正常解。
2 圆走航观测模式分析
无论采用非差观测定位模型,还是历元间差分观测模型,其所有声学测距数据所组成的误差方程可简写为
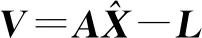
(18)
式中,V为残差;A为设计矩阵;L为观测向量。
2.1 圆走航模式下几何强度分析
在圆走航模式下,以声学应答器为圆心进行测量(图1)。设γ为第i次测量声学测距与垂线方向的夹角,βi为测量半径方向与水平坐标系E轴的夹角,则非差定位模型式(9)的设计矩阵可写为
(19)
圆走航模式下,水声测距观测可近似认为是等权观测,则非差观测定位模型的法矩阵N为
(20)

(21)

非差观测定位模型的精度衰减因子DOP为
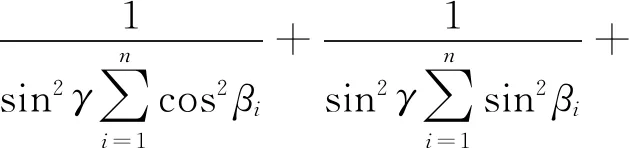
(22)
在圆走航模式下,相邻历元声学测距与垂线方向的夹角没有变化,即γi=γi+1,对前后历元进行差分,其总误差方程的设计矩阵变为

(23)
在不考虑观测量之间相关性的前提下,历元间单差观测定位模型的N矩阵为
N=ATPA≈
(24)
(25)
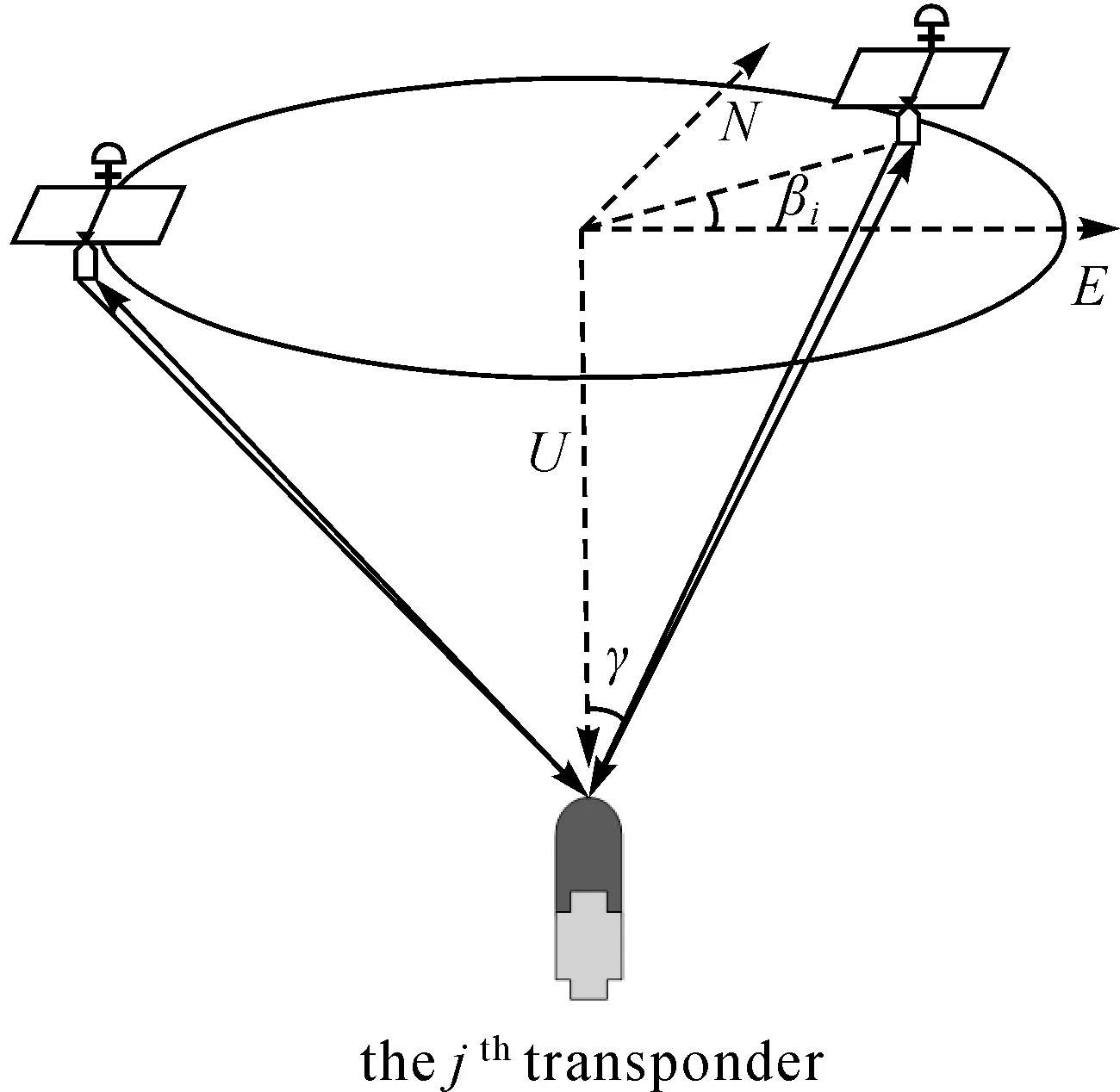
图1 测距示意Fig.1 Ranging diagram
单差观测定位模型其平面精度衰减因子HDOP为
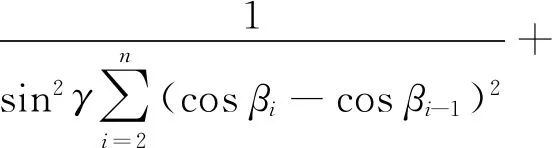
(26)
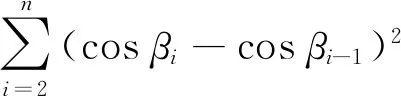
2.2 圆走航模式下最佳观测半径
在单位权方差因子一定情况下,位置精度衰减因子PDOP越小,表明点位精度越高。圆走航模式下非差观测的a、b、c间的关系[15,35]为
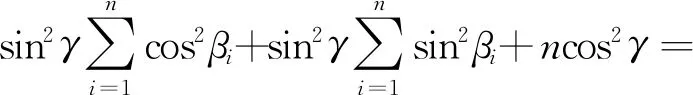
nsin2γ+ncos2γ=n
(27)
可构造如下拉格朗日函数
(28)
求偏导,并令
(29)
将式(29)代入式(27),解得
(30)
设r是走航半径,则有
(31)
则圆走航模式最佳测量走航半径为
(32)
(33)
式中,σ0为水声测距精度。
如果仅考虑平面位置精度最高,即要求[14]

(34)
采样率一定情况下,要使HDOP2最小,即要求sin2γ取值最大,则有
(35)
由于水深u是一固定值,即要求最佳走航半径为
r=u
(36)
平面位置理论精度为

(37)
(38)
即要求最佳走航半径为
r=0
(39)
式(39)表明,要使垂直分量精度最高,应在水声应答器过顶方向进行重复观测,其理论精度为
(40)
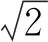
从前文推导可以看出,不同的测量半径对定位误差各分量的影响存在明显差异,实际测量时,航迹设计为半径等于水深的圆形航迹加过顶十字交叉航迹。这种测量轨迹的组合既满足了水平方向精度最佳,也满足了深度分量精度的要求,不仅有利于测量轨迹控制,也有利于提高测量效率。
2.3 圆走航模式下测距系统误差的影响
在式(6)中,通常将综合性误差δρ纳入随机误差考虑。事实上,综合性误差δρ是系统性误差,并不完全具备随机误差[4,6]。由式(10)可知,综合性误差对海底大地基准点坐标影响为
(41)
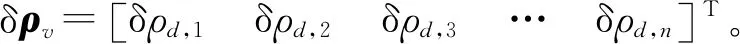
圆走航观测可认为是等权观测,由式(19)、式(21)、式(41)得测距综合性误差对定位结果的影响为
(42)

(43)
即圆走航下测距系统误差是近似常数δρv0,对定位结果的影响为
(44)
可以看出,测距系统误差对水平方向坐标的影响几乎为0,而对垂直分量的影响较大,垂直分量的误差取决于开角γ和测距误差δρv0的大小。开角γ越大,测距误差δρv0也越大,对垂直分量影响越大;开角γ越小,测距误差δρv0也越小,对垂直分量影响也越小。
3 算例与分析
本文分别用模拟仿真数据和深海实测数据进行分析。
3.1 模拟算例分析
水声测距误差通常采用式(45)[33]表示
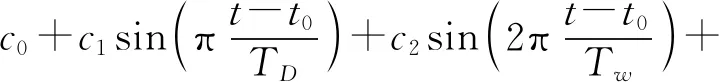
(45)
测距误差主要包括:第1项是常数误差,通常由声速未标定误差引起;第2项和第3项是声速变化引起的长周期项和短周期项误差,参照文献[4]在北太平洋的试验和文献[6]在夏威夷岛附近的试验,测距误差中的长周期项与潮汐变化规律近似,周期为12 h,振幅约20 cm,测距误差短周期项一般由内波引起,周期从几十分钟到几个小时不等,t0是初始时刻,t是任意时刻,其中TD是指长周期项,Tw是指短周期项;第4项是测区相关性误差,与距离变化有关,x是t时刻声学换能器的三维坐标,x′是海底应答器的三维坐标;第5项为随机性误差。
本文进行如下仿真试验,测量船以应答器的垂直投影为中心进行圆走航测量一周。水下应答器的深度为5000 m,为使水平位置精度最高,圆走航模型的最佳走航半径应等于水深,即测量半径为5000 m,每20 s进行一次测距,共获得4320个水声测距观测数据。测距误差模拟采用式(45)计算,随机性误差为方差2 cm的正态分布,其他参数配置见表1。模拟中除考虑测距误差外,还考虑测量船定位误差,水平方向的定位精度为5 cm,垂直方向定位精度为10 cm。

表1 模拟观测系统参数设置Tab.1 Parameter setting of simulated observation system
图2给出了内波引起的短周期误差、日月潮测距误差、测区相关性误差以及总的误差大小;由于考虑内波误差和不考虑内波误差对非差定位模型设计矩阵系数的值影响非常小,对差分定位模型设计矩阵系数的值影响也小,图3仅给出考虑内波误差较小情形下的非差、差分模型在N、E、U方向的设计矩阵系数,表2给出了非差定位模型和差分模型确定的N、N-1;图4给出了考虑内波误差和不考虑内波误差情形下的非差和差分定位模型确定的残差,表3给出了不同方案计算的残差统计;表4给出了测距误差考虑内波误差的非差和差分计算模型的结果精度统计,测距误差不考虑内波误差的非差和差分计算模型的结果精度统计也在表4中。
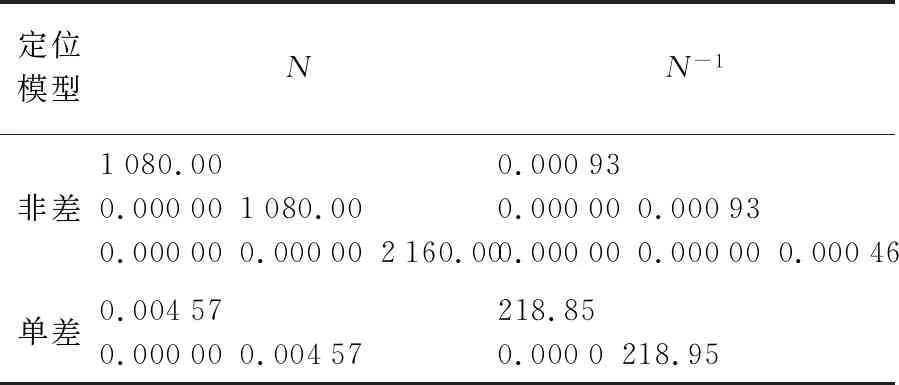
表2 不同定位模型下计算的矩阵N、N-1Tab.2 N、N-1by different positioning models
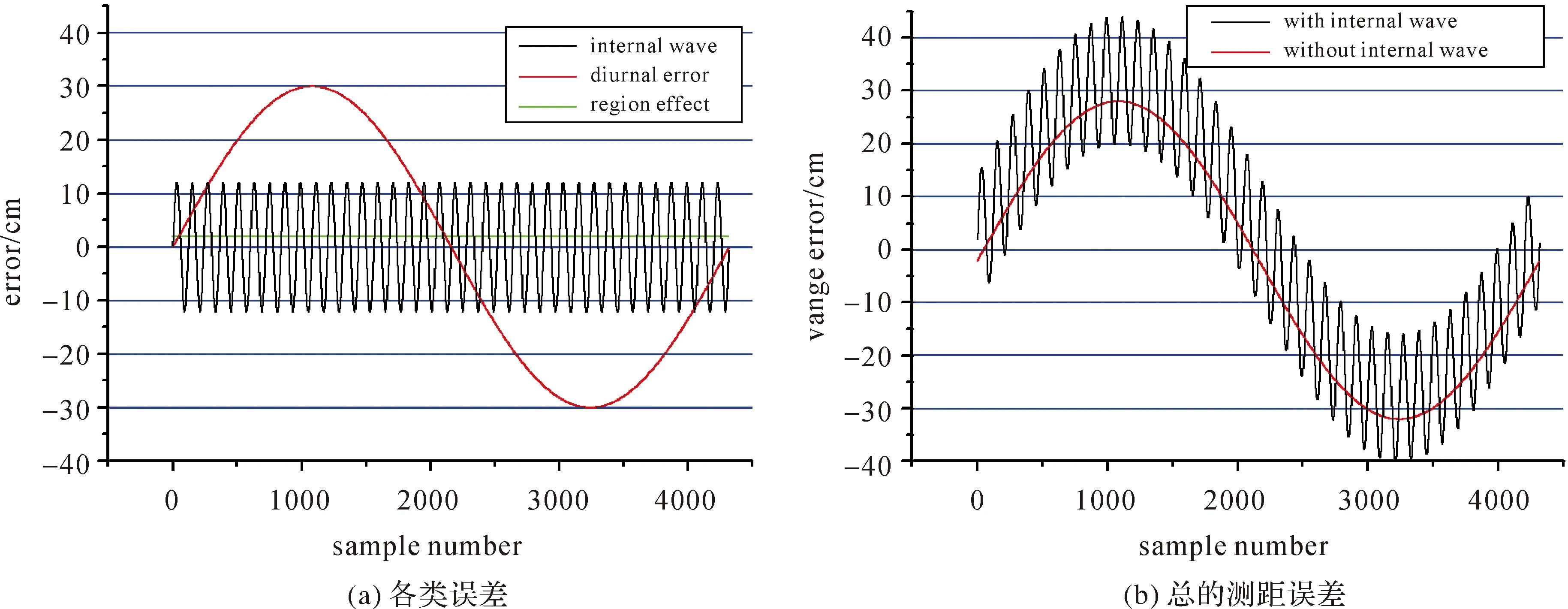
图2 测距误差大小Fig.2 Ranging errors
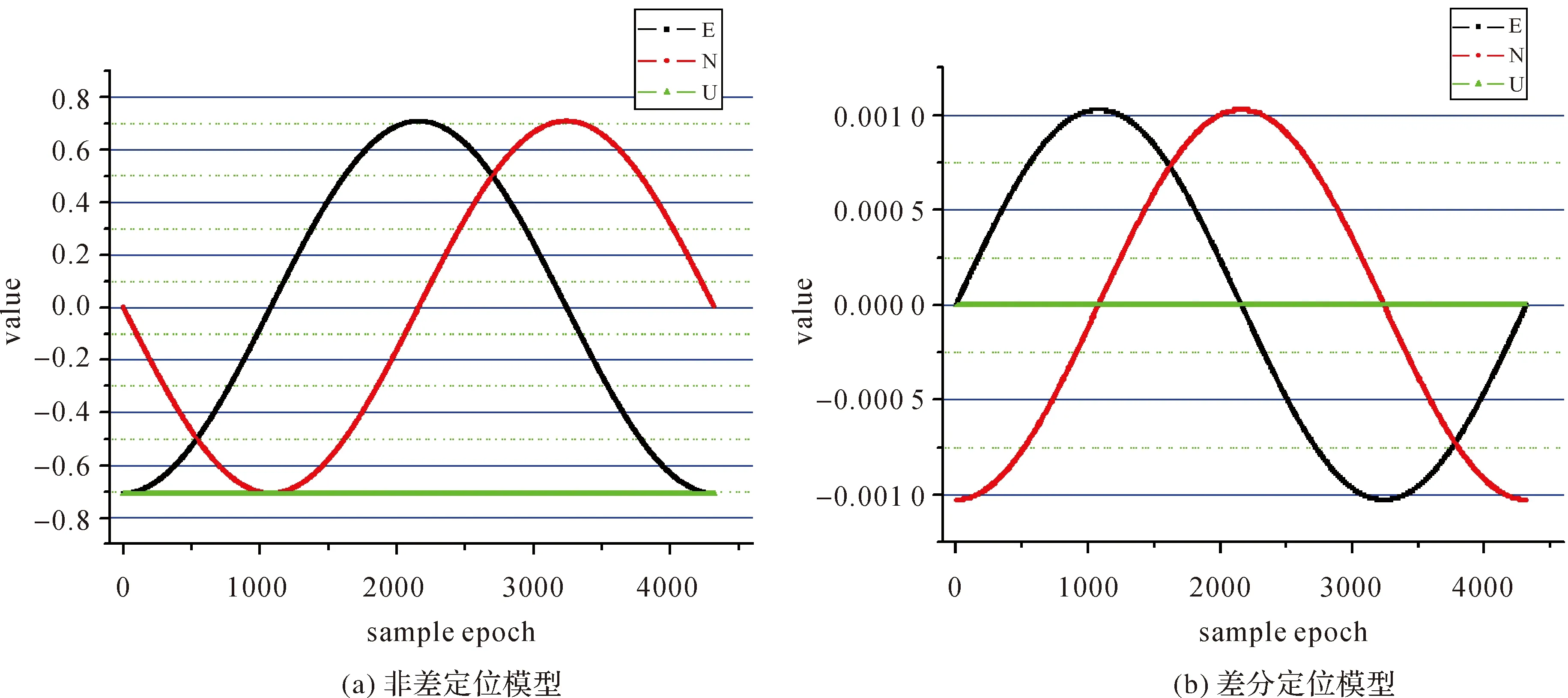
图3 设计矩阵Fig.3 Design matrix
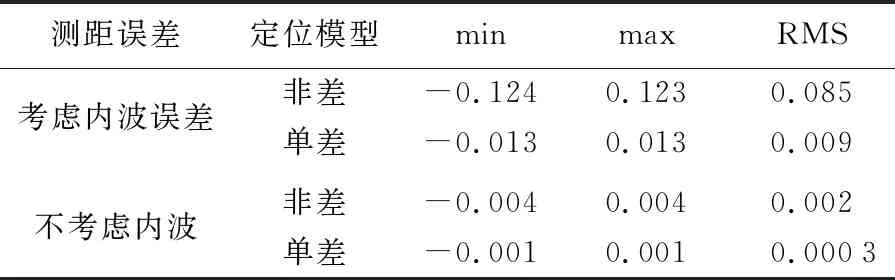
表3 不同定位模型下的残差统计Tab.3 Residual statistics by different positioning models m
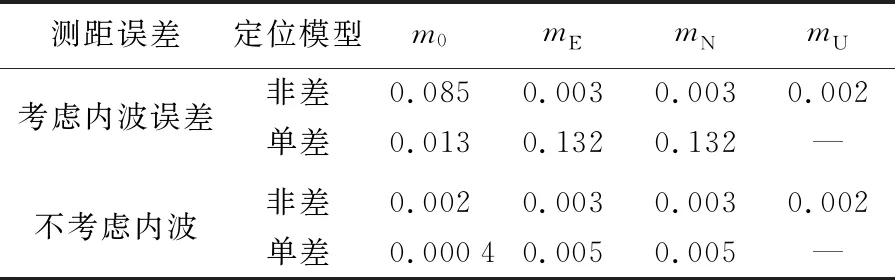
表4 不同定位模型下的定位精度统计Tab.4 Statistics of positioning accuracy by different positioning models m
可以看出:
(1)从观测几何结构看,非差定位模型设计矩阵N、E方向元素值呈正弦变化,振幅达到约0.7,而U方向元素的值几乎为一常值约0.67,计算得到的法方程阵N的主对角线元素的值较大,达到1080、1080与2160,其协因数阵N-1的主对角线元素的值非常小,仅0.000 93、0.000 93和0.000 46,这说明其观测几何结构较好,对参数的求解非常有利;历元间单差模型下设计矩阵N、E方向元素的值也呈正弦变化,但振幅非常小,仅达到0.001,而U方向元素的值接近零,计算得到的法方程阵N的主对角线元素的值相对较小,仅为0.004 5、0.004 5,其协因数阵N-1的主对角线元素非常大,达到218.85、218.95,这说明历元间差分后观测几何结构变差了,参数的求解易受观测异常的干扰。
(2)从计算残差看,测距误差考虑内波的定位模型计算的残差大于测距误差不考虑内波的定位模型。测距误差考虑内波时,非差模式计算得到的残差最大达到0.12 m,其单位权中误差为0.085 m,而差分模式下计算得到的残差最大约0.013 m,单位权中误差仅为0.009 m;测距误差不考虑内波时,非差模式计算的单位权中误差为0.002 m,而差分模式的单位权中误差仅为0.000 3 m。这说明差分模式计算得到的残差较非差模式要小得多,主要是因为差分将绝大部分测距误差消除掉了,即差分消除了常数误差和声速变化引起的长周期项,短周期项误差大部分也被消除,仅保留了残余测距误差。
(3)从定位参数精度看,差分模式将绝大部分测距误差消除掉了,残余测距误差较小,估计的位置结果精度应该高,但计算结果发现,差分模型定位结果的精度比非差模型精度低一个数量级。测距误差考虑内波时,非差模式下平面位置各分量精度为0.003 m、0.003 m,而差分模式下位置精度为0.132 m、0.132 m;测距误差不考虑内波时差分模式下位置精度为0.005 m、0.005 m。这主要是因为差分后设计矩阵结构变差了,使得差分模型的N-1对角线元素的值明显变大,观测误差的影响被放大了。
(4)试验中也进行了圆走航半径为1.5倍水深的模拟试验,由于篇幅所限没有给出详细的图表,但与圆走航半径等于水深的结论分析相同,只是各类数值不一样。同样,也进行了基准点顶部观测的数据模拟,基准点水深估计值受各类误差累计影响,测距误差越大,对垂直分量影响就越大。
3.2 实测算例分析
为检验分析,采用一次深海试验数据进行分析。试验水域水深约3000 m,水下地形平坦,在海底布设1个水声应答器作为水下大地基准点,测量船以应答器为圆心、半径约为水深进行圆走航方式测量一周,但由于测量船控制等原因,实际测量并不是标准圆(图5)。测量时船速约4 n mile/h,测量耗时约1.5 h,每8 s进行一次水声测距,共获得683个水声测距时延数据。利用GNSS星基差分接收机,测量获得测量船GNSS天线的位置,采样率为1 Hz;同时,利用姿态测量设备获得测量船姿态,采样率为5 Hz。测量前,严格测定船载水声换能器、GNSS天线、姿态设备在船体坐标系下的坐标。如此,利用测得的载体GNSS天线位置、姿态数据和标定的GNSS天线到换能器偏差数据,通过姿态转换非常容易得到声学换能器的位置。此外,测量期间还进行了声速剖面测量,以获得水声声速剖面(图6),利用测得的声速剖面数据采用声线跟踪算法以计算换能器到水下大地基准点之间的距离。
表5给出了非差定位模型和差分模型确定的N、N-1;表6给出了非差和差分定位模型的定位结果;表7给出了不同定位模型下的残差统计;图7给出了设计矩阵系数;图8给出了计算残差。
(1)从图6可以看出,声速剖面在100 m内的浅层变化较大,100 m以深呈明显的抛物面变化。在100 m处声速约1548 m/s,1000 m处约1485 m/s,3000 m处约1510 m/s,即1000 m以浅声速变化呈负梯度变化,而1000 m以深声速变化呈正梯度变化。
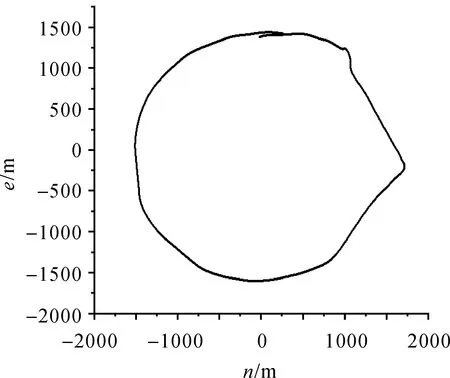
图5 测量航迹图Fig.5 Survey ship track
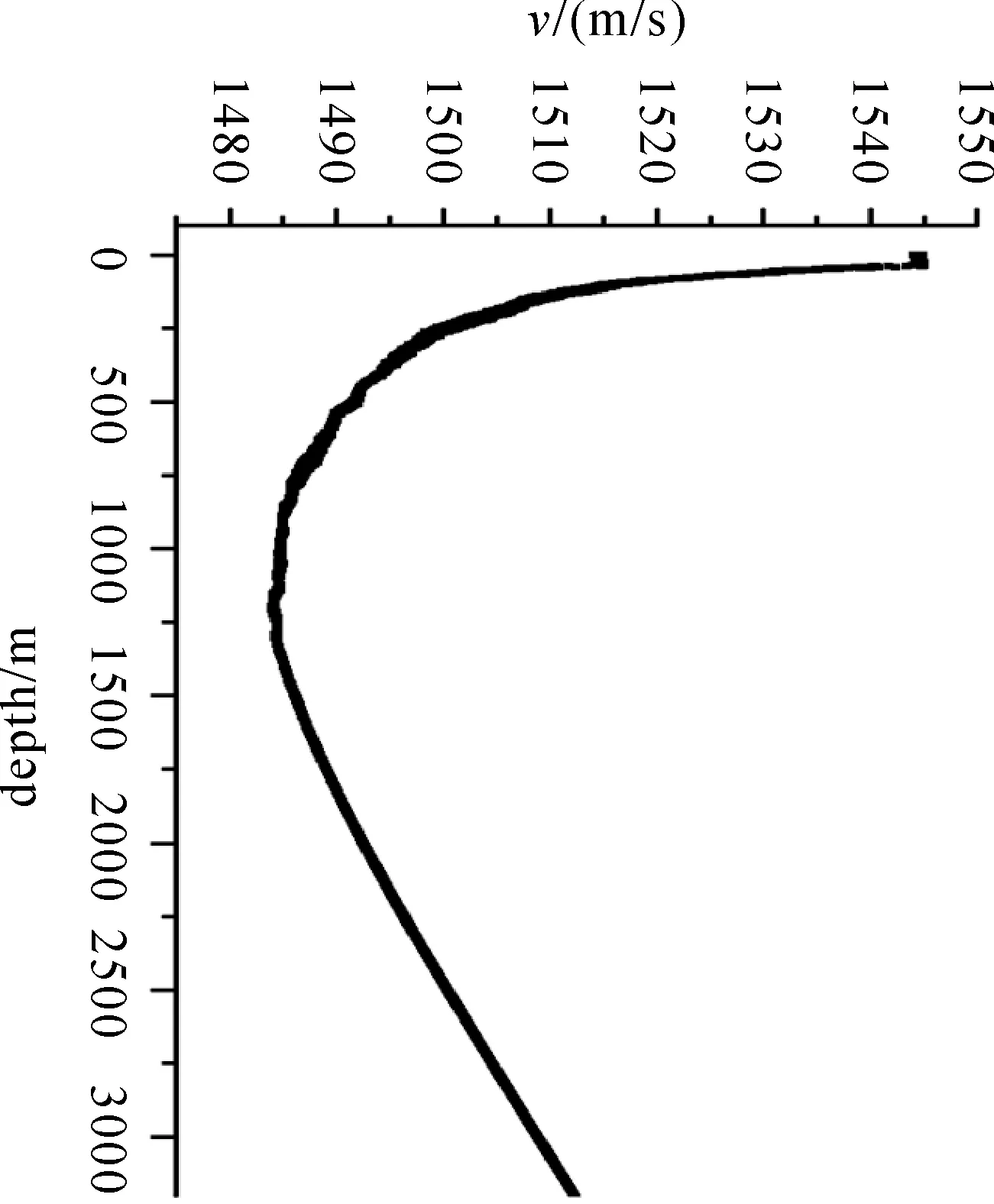
图6 测量声速剖面Fig.6 Sound velocity profile

表5 不同定位模型下计算的矩阵N、N-1Tab.5 N、N-1 by different positioning models

表6 不同定位模型下的定位精度统计Tab.6 Statistics of positioning accuracy of different positioning models m

表7 不同定位模型下的残差Tab.7 Residuals by different positioning models m
(2)从图7可以看出,非差模型计算的设计矩阵N、E方向元素值基本呈正弦分布,振幅达到约0.5,而U方向元素有轻微变化,但基本为一条直线,其值约为0.9;差分模型的设计矩阵N、E方向元素也具有正弦趋势特性,振幅较小仅有0.005,U方向元素也基本为一条直线,但有轻微浮动。设计矩阵系数直接反映了观测几何强度,即非差观测模型的观测几何强度明显优于差分观测模型。
(3)对比实测数据的图7和仿真数据的图4,它们计算的设计矩阵的变化趋势基本一致,但在数值上有明显差异。实测数据差分模型的设计矩阵元素具有明显的抖动,而仿真数据确定的设计矩阵元素数值较小,但图形非常平滑。这主要是由于测量船控制原因,其测量航迹为近似圆,而模拟数据的测量轨迹为标准圆。
(4)对比表5中不同定位模型的法矩阵N,非差定位模型的法矩阵N的主对角元素较大,在E、N、U方向的数值分别达到67.8、68.4、547.7,其协因素矩阵N-1的主对角线元素的值较小,仅为0.015、0.015和0.002;差分定位模型的法矩阵N的主对角元素的值非差小,仅为0.012、0.014和0.000 2,而其协因素阵主对角线元素的值较大,达到87.79、77.5和6 553.2。这也说明,非差观测模型的观测几何强度明显优于差分观测模型。
(5)从结果看,非差定位模型、差分定位模型的单位权中误差为0.21 m、0.28 m,其差异并不大,差分模型虽然削弱了系统误差的影响,但随机误差却增大了;非差定位模型点位坐标的内符精度为0.026 m、0.026 m和0.009 m,差分定位模型的内符精度却达到2.6 m、2.6 m和22.68 m,这说明非差观测模型的定位结果精度优于差分观测模型结果。
(6)从图8可以看出,无论非差定位模型还是差分定位模型,其残差均存在一定周期现象,可能与海洋内波等系统误差的影响有关。非差定位模型的残差的最小值、最大值和RMS分别为-0.748 m、0.731 m和0.210 m,差分定位模型分别为-0.856 m、0.834 m和0.198 m,这两种模型的残差的统计差异并不大。这点与仿真数据的结论明显不同,这说明实测数据的影响因素较模拟数据所考虑的因素要复杂得多。
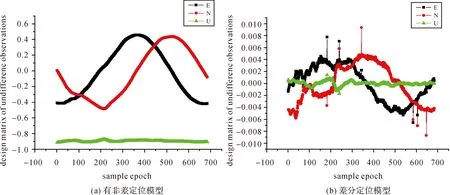
图7 设计矩阵Fig.7 Design matrix

图8 非差和差分定位模型计算的残差Fig.8 Residuals calculated by the undifference and difference positioning model
4 结束语
本文对圆走航模式下水下基准点的定位效能进行了系统分析。分析了声速剖面变化等系统误差对定位结果的影响,详细讨论了声学测距非差定位模型和削弱系统误差影响的历元间差分定位模型,并对圆走航模式下非差、差分对位置参数的可测性、不同分量位置精度的最佳测量半径、测距误差的影响等进行了系统分析,给出了其适用性条件,利用仿真和深海实测数据进行了详细验证。
(1)从参数可估计性看,非差定位模型对三维位置参数均可估,如要同时估计位置参数和系统误差参数,垂直分量与系统误差参数往往不可分;历元差分定位模型消除了大部分系统误差,仅能够估计平面位置参数,而垂直分量参数不可估。在非标准圆观测模式下,非差、差分模型均可估计三维位置参数,但历元差分定位模型估计的垂直分量参数的精度一般会较低。
(3)圆走航模式下测距系统误差对位置水平分量的影响较小,几乎为零,而对垂直分量有影响与测量开角(即测量半径)大小有关,与测距误差的大小成正比,开角越大,测距误差也越大,对垂直分量影响越大;开角越小,测距误差也越小,对垂直分量影响也越小。为削弱测距系统误差的影响,测量模式采用对称观测,提高垂直分量精度,建议采用多次过顶观测并辅以多源手段消除单一手段的系统误差。

