利用南山数据对PSR B0329+54的长时标轮廓稳定性的研究∗

陈建玲 王洪光 温志刚 王 娜 吕成冰 闫文明

(1 运城学院物理与电子工程系运城 044000)

(2 中国科学院新疆天文台乌鲁木齐 830011)

(3 广州大学天体物理中心广州 510006)

1 引言

脉冲星是高速旋转且具有强磁场和强引力的致密天体.当脉冲星的辐射束扫过地球时,我们就会接收到周期性的脉冲信号.观测发现,脉冲星的单脉冲无论是形状还是强度都是极不稳定的,但是如果将足够多的单脉冲按照周期进行同步叠加,大多数脉冲星就可以得到很稳定的累积脉冲轮廓[1].对于少数脉冲星,其累积脉冲轮廓在两种或者多种形状之间切换,这就是脉冲星的模式变化现象,如对于PSR B0329+54、PSR B1237+25和PSR B1822−09等源都探测到了模式变化现象[2–4].一般认为,持续时间较长的模式是正常模式,而持续时间较短的模式为反常模式.目前发现有模式变化的源大约有60多颗[5].PSR B0329+54是一颗典型的模式变化脉冲星,它流量很强,且模式变化频繁.前人工作表明,这颗源的累积脉冲轮廓大约有85%的时间处于正常模式,而其余15%的时间处于反常模式,正常模式和反常模式的主要区别表现在轮廓不同成分之间相对强度的变化[6–7](如图1所示,文献[7]中图4).

Helfand等人在1975年(以下简称HMT75)研究了12颗轮廓形状较复杂脉冲星的轮廓稳定性时标,他们发现每颗星都有典型的特征时标,在积分时间达到这个特征时标后,就可以得到稳定的累积脉冲轮廓,并且每颗脉冲星的特征时标和其他辐射特性之间存在着一定的相关性.例如,有子脉冲漂移现象的脉冲星具有较短的特征时标,而轮廓中有多峰成分的脉冲星特征时标较长[8].Rathnasree等人分析了28颗脉冲星的平均轮廓,其中有部分源和HMT75是重复的,得到了和HMT75相似的结论[9].这些工作表明,对于正常脉冲星,一般最多叠加10000个单脉冲就可以得到非常稳定的累积脉冲轮廓.而对于毫秒脉冲星,Kramer等人研究了毫秒脉冲星PSR J1022+1001,发现这个源的稳定性时标要比正常脉冲星长得多,大约需要叠加几十万个单脉冲[10].Shao等人也研究了这颗毫秒脉冲星轮廓的稳定性,发现这颗脉冲星轮廓有两个成分峰值的比例随时间发生变化[11–12].

HMT75的工作包括了PSR B0329+54这颗源,他们得到的结论是,这颗星在1.4 GHz上正常模式的稳定性时标大约是500个单脉冲,对应时间大约为6 min,而反常模式的稳定性时标约为3000个单脉冲,大约36 min.他们的结果揭示了一个更为有趣的现象:当积分时间达到大约1 min时,积分轮廓趋于稳定的速率发生转折,正常模式变快,反常模式变缓,延续到积分时间10 min左右.但是他们的数据时长较短,无法回答这种差别是否会延续到更长的积分时间上.

2003年以来,新疆天文台南山25 m射电望远镜对PSR B0329+54进行了长期监测,积累了丰富的观测数据,其中2004年3月将近20 d的准连续观测大约持续了360.2 h,是目前同类研究中时间最长的.利用2003到2009年共约521 h的数据,Chen等人成功地得到了正常模式和反常模式持续时标的分布[7].HMT75所用的9段数据时长只有小时量级,相比之下,新疆天文台的观测为研究这颗源在更长时标上的轮廓稳定性提供了宝贵的数据.本文的目的是利用2003至2009年的观测数据来研究正常模式和反常模式脉冲轮廓的稳定性时标,并对HMT75的结论进行检验.本文第2节介绍了观测数据,第3节给出了正常和反常模式轮廓稳定性时标的分析方法和结果,并与HMT75的结果进行了对比,第4节探讨了轮廓趋稳速率在不同时标上有差异的原因,第5节进行了总结.

2 观测数据

PSR B0329+54是新疆天文台南山25 m射电望远镜脉冲星到达时间长期监测项目的目标之一.我们选取了2003–2009年中90次0.5 h以上的观测数据(单次最长为3 h),共160.8 h,以及2004年3月12日至31日的将近20 d的准连续数据,共360.2 h,数据列表详见文献[7].准连续观测分为两段,每一段持续8 d,中间有2.3 d的间断,前8 d和后8 d的持续时间分别为182.0 h和178.2 h.消色散系统采用了2×128×2.5 MHz的滤波系统,观测中心频率为1540 MHz,总带宽为320 MHz.每个脉冲周期有256个采样点.对于观测系统更详细的介绍可见Wang等人2001年的文章[13].为了提高信噪比,观测时对80个脉冲周期进行叠加后得到一个子积分轮廓,子积分时间约为57 s.

PSR B0329+54的轮廓形状比较复杂,Rankin把这颗源的累积脉冲轮廓分类为3峰或者可能的多峰类型[14],利用高斯分离的方法,它可以被划分为5个成分[15]甚至9个成分[16].考虑新疆天文台的观测采样点较少,在我们2011年研究模式变换时标的工作中[7],将累积脉冲轮廓划分为3个成分:成分I (前导成分)、II (中心成分)和III (后随成分),如图1所示,本文沿用了这种成分划分方法.由于轮廓形状的变化主要表现在成分I和成分III之间的相对强度的变化,所以我们用比例R=I1/I2来表示轮廓形状的变化,其中I1和I2分别表示成分I和成分III的积分强度,计算方法详见文献[7].正常模式的比值R绝大多数在0.35–0.8范围内变化,而对于反常模式,绝大多数的R在0.7–1.8范围内变化.我们检查了正常模式和反常模式的比值随时间变化的时序图,发现20 d的准连续观测中前66 h的数据,正常模式比值的时间序列呈现出明显的弓形,经核查,这是由于累积脉冲轮廓的基线不平造成的,因此我们删除了这一段数据.这样20 d的观测数据留下了约250 h (16089个子积分轮廓脉冲)的正常模式和42.3 h (2719个子积分轮廓)的反常模式的轮廓.90次观测的数据总共大约有133.3 h (8049个子积分轮廓)的正常模式和27.7 h(1676个子积分轮廓)的反常模式轮廓.下面我们分别利用两种不同的方法对20 d的准连续观测数据和90次的观测这两部分数据进行详细分析.

3 两种模式的稳定性时标分析

HMT75分析累积脉冲轮廓稳定性时标的方法是基于相关系数的.为了和HMT75的工作进行比较,本文也首先采用了相关系数的方法.但我们也注意到一点,相关系数的值来自于轮廓中所有成分的贡献,理论上,不排除不同成分的强度和形状的涨落特征不同,这样的话,仅凭相关系数可能不能有效地反映这种差别对轮廓稳定性的影响.前人的观测表明在2 GHz以下,在两种模式中成分II都强于其他两个成分,它对相关系数值的贡献可能会比较大[6].已有观测表明,这3个成分的辐射特征有差别,例如,成分I和II的谱指数相近,但成分III与它们有一定差别[17],又如,成分II和其他两个成分的偏振特征有明显差别[18].尽管文献中尚无关于3者在强度和形状上涨落的研究结果,但它们有可能是不同的.

根据如上考虑,为了研究不同成分相对强度的涨落对轮廓不稳定性的影响如何,我们还采用了另一种直接的方法,即考察成分I对II的强度比值R12、I对III强度比值R13、以及III对II的强度比值R32的涨落水平随积分时间的变化.其基本原理是,对同一种模式,我们将所有的数据按照设定的积分时间分成若干段,对各段分别叠加得到相应的积分轮廓,并计算这些轮廓的比值R,再计算这些比值的标准方差σR,以此表征比值的涨落水平.显然,如果轮廓随积分时间增加趋向于稳定,那么σR值就不断减小;如果趋于稳定的方式发生变化,那么σR减小的速率就会发生变化.因此,σR随积分时间的变化曲线可以用来考察累积脉冲轮廓中不同成分趋向于稳定的行为,并帮助确定特征时标.

3.1 基于相关系数的方法

HMT75的方法是对每一种模式首先叠加所有的单脉冲产生参考累积脉冲轮廓,然后变化子积分时间,依次叠加N=2n个单脉冲,形成一系列的子积分轮廓,其中n取0或正整数,但是N的最大值要小于单脉冲总数的一半,以保证至少有两个独立的子积分.将每一个子积分轮廓和参考轮廓做交叉相关,得到所有子积分相关系数的平均值ρ.HMT75用1−ρ随积分时间的变化来衡量轮廓的稳定性,如果轮廓随积分时间增加而更趋于稳定,那么相关系数就趋向于1;如果在不同时间尺度上趋于稳定的方式不同,那么相关系数—积分时间曲线就会出现拐折.他们认为当ρ0的值为0.9995时,对应的N值即为达到稳定的轮廓时所需要叠加的数目[8].

由于我们没有单脉冲的数据,而是经过1 min左右叠加的子积分脉冲轮廓,所以不能照搬HMT75的方法;另外,按照2的倍数递增积分时间,会带来数据点过于稀疏的问题,不利于观察相关系数曲线是如何拐折的.我们采取以下步骤:首先叠加所有同种模式的子积分轮廓,分别得到正常模式和反常模式的参考轮廓,然后设定一个积分时间,例如m整数倍的子积分时长,得到一系列积分轮廓,再将它们与参考轮廓做相关,得到Int(Mtot/m)个相关系数,其中Mtot为子积分总数,Int为取整运算.取这些相关系数的平均值ρ,作出1−ρ与积分时间τ的关系图,如图2所示.图中红色的实线表示90次非连续观测,蓝色的实线表示20 d准连续观测;为了对比,同时也复制了HMT75的数据在1400 MHz上的正常模式和反常模式的结果(黑色的实线).

在图2中可以看出,无论是正常还是反常模式,我们的1−ρ曲线的斜率整体上发生两次拐折,因此可近似看作3段幂律函数.对于正常模式,拐折的积分时间约为3–5 min和80–200 min,在前一个拐折区域斜率由陡变平,在后一个区域由平变陡,这意味着随着积分时间增加,脉冲轮廓形状趋于稳定的速度由快变慢,而后再变快.反常模式的1−ρ曲线也表现出类似的特征,但是拐折时段略有不同,分别约为3–5 min和50–80 min,这两组时标在表1中表示为τk1和τk2.

HMT75指出,如果脉冲轮廓形状的不稳定性是完全独立的随机涨落造成的,应该有(1−ρ)∝τ−0.5.我们对20 d观测数据的正常模式和反常模式的曲线进行了分段线性拟合,即lg(1−ρ)∝klgτ.用于拟合的3个时间段避开了拐折区域,正常模式的分别为1–2 min (只有两点,直接计算)、7–70 min和250–5000 min,反常模式的分别为1–2 min、7–40 min和100–1000 min,得到的斜率k如表1所示.下标“1、2、3”分别表示上述3段拟合分区,作为对比,表中k0列出了HTM75得到的1−ρ曲线在1个脉冲周期到大约1 min时间段内的斜率.结果表明,除了20 d观测数据中第1时间段,即积分时间在1–2 min内,斜率接近−0.5,其他各段都显著偏离−0.5 (包括HTM75在短时标上的斜率),表明在绝大多数积分时间段内轮廓形状的不稳定性都不是完全独立的随机涨落过程,而是存在着一定程度的相关性.

表1 基于20 d数据的lg(1−ρ)−lg τ关系的分段拟合参数.其中τk1和τk2表示曲线的拐点时标, k0表示HMT75得到的曲线的斜率, k1、k2和k3表示对曲线的3段时间区间分别拟合得到的斜率Table 1 The best-fit slope rates for the lg(1−ρ)−lg τ curves based on the 20-day observation. τk1 and τk2 are the turning points of the curves. k0 is the slope rates obtained by HMT75. k1, k2 and k3 are the slope rates for the curves in three time segments

我们将本文和HMT75的结果进行了对比.因为我们的数据子积分时间约为57 s,所以我们无法比较低于这个时间尺度的1−ρ的变化.从图2可以看出,在本文和HMT75重合的积分时间上,本文得到的1−ρ的数值要更大,这表明基于新疆天文台数据的轮廓相关性没有HMT75的高.对于正常模式,在两部分数据重合的时间区域上(1–10 min),我们的数据和HMT75中的1−ρ的数值都呈现下降的趋势.但是HMT75的下降更快,而我们的数据下降得更平缓,而且整体的下降趋势可以分成两段,在1–2 min左右下降趋势更陡一些,后面的下降趋势要平缓一些.对于反常模式,在两部分数据重合的时间区域上(1–8 min),我们的数据和HMT75的结果趋势基本一致,但我们的数据在2 min左右有一个拐折,在2 min之后下降的趋势要比1–2 min更加平缓一些,这从表1中两种模式的斜率参数k0、k1和k2的数值也可以看出.

造成本文和HMT75结果有一定差异的原因有:(1)数据采样点数bin,我们的数据用的是南山25 m射电望远镜,采样点数是256,HMT75在1400 MHz所用的数据是国家射电天文台(National Radio Astronomy Observatory,NRAO)的42 m口径射电望远镜,采样点数为512.(2)我们没有单脉冲的数据,得到的原始数据是1 min的积分轮廓,所以对应数据点的横坐标只能是1 min的倍数.而HMT75有单脉冲的数据,所以对应数据点的横坐标为单脉冲周期(0.714 s)的倍数,所以在较短的时标上和HMT75的结果有一定的差异.(3)我们用的是2003–2009年的数据,而HMT75所用的是1971年和1972年的数据,两者时间间隔30多年,所以1−ρ的数值有系统性的差异.但是我们的数据优势在于总时间更长,覆盖了更长的时标和更长的积分,弥补了HMT75在10 min以上时间区域的空白.

正如HTM75自己指出的那样,选择交叉相关系数0.9995作为稳定时标的判据是有任意性的.由于我们得到的相关系数明显低于HTM75的数值,如果仍沿用此标准,得到的时标将远大于HTM75的结果.综合HTM75和我们的结果,两种模式的1−ρ曲线均只有一个较平缓的区域,因此我们认为,选择轮廓形状稳定速度由快变慢的转折期τk1的终点,即将轮廓开始进入慢速趋稳阶段所需的积分时间作为稳定时标的判据更为合理.以此判据,根据上述结果,可以定出正常模式和反常模式轮廓的稳定时标都近似为5 min.

3.2 基于比值R的标准方差的方法

对90次非连续观测,我们首先删掉信噪比较低的轮廓,之后根据比值R将正常和反常模式的子积分序列分开.由于不同时间段观测的脉冲轮廓有相对相位差,所以我们采用将各时段的积分轮廓与一个高信噪比的参考轮廓进行相关的方法,将各时段的轮廓进行了对齐,修正了相对相位差;然后按时间顺序,分别将所有的正常模式和反常模式的子积分数据相连,得到了两个模式的子积分数据长链,分别包含8049个正常模式和1676个反常模式子积分轮廓,相应时长分别为133 h和27.8 h.接下来进行轮廓叠加,按照给定的积分时间,将正常模式的数据长链切分成若干段,对每一段数据进行叠加,得到若干个累积脉冲轮廓.然后对每一个轮廓都计算出比值R,再求出这些轮廓R值的标准方差σR.积分时间依次选择为2、3、···、N倍的子积分时间(每个子积分约为57 s).这里应当保证叠加后得到的积分轮廓数目不少于3个,求出的标准差才有意义,即Ntot/N≥3,其中Ntot为数据长链中子积分轮廓总数.

对于20 d的准连续数据,采用相同的方法得到了两种模式子积分数据长链,分别有16089个正常模式和2719个反常模式的子积分轮廓,时间长度约为90次不连续观测的两倍.我们并没有把90次和20 d的数据进一步合并,而是独立使用,因为他们的时间跨度不同,前者跨越7 yr,后者延续20 d,基于这两组数据的σR−τ曲线可以进行比较.

图3给出了成分I和III强度比R13的σR13−τ曲线(黑色),成分I和II强度比R12的σR12−τ曲线(蓝色)以及成分III和II强度比R32的σR32−τ曲线(红色),左图为正常模式,右图为反常模式,实线为20 d准连续观测数据,虚线为90次非连续观测数据.从图3中可以看出,无论是正常模式(图3左图)还是反常模式(图3右图),同种颜色的线在纵向维度上有明显的平移,这反映了不同时段的观测之间有系统性的偏差.另外,即使是对于同一组观测数据(20 d的准连续或90次观测数据),正常模式和反常模式的σR13曲线都有明显的偏移,这反映了正反模式之间有系统性偏差.尽管90次和20 d的数据在时间跨度方面差别很大,但它们的σR−τ曲线在形状上表现出高度的一致性.将这3种曲线和1−ρ曲线进行综合比较,主要特征可以归纳如下:

(1)对于3种比例,在双对数图上正常模式的σR−τ曲线都呈现出3段拐折的特征:先是快速的下降,而后进入较缓慢下降的阶段,再进入快速下降阶段.但3种曲线斜率转折的时间段不同,表2中τb1和τb2分别是斜率由陡变缓和由缓变陡的拐折时段(根据20 d数据得到),可以看出σR32曲线的两个拐折时标要短于其他两种曲线,和1−ρ曲线的非常接近.此外斜率也有不同,σR32曲线和其他两种曲线的差别主要体现在τ >τb2的长时标上斜率要缓一些.作为参考,我们对20 d数据的σR−τ曲线扣除拐折时段后,用lgσR13∝algτ关系做了分段拟合,短、中、长3个积分时标上的斜率a1、a2和a3在表2中给出,从数值上看σR32曲线3段斜率的对比和1−ρ曲线的更接近些;

(2)反常模式的σR−τ曲线整体上也表现出和正常模式类似的行为,表2中给出了20 d数据3种曲线相应的拐折时标以及分段斜率,时标后面标注“?”号的表示曲线中有拐折的迹象,但不十分肯定.显然,σR12曲线的拐折时标和曲线形状都和1−ρ曲线更加接近,而σR13和σR23曲线在长时标上与中等时标的斜率差别不大;

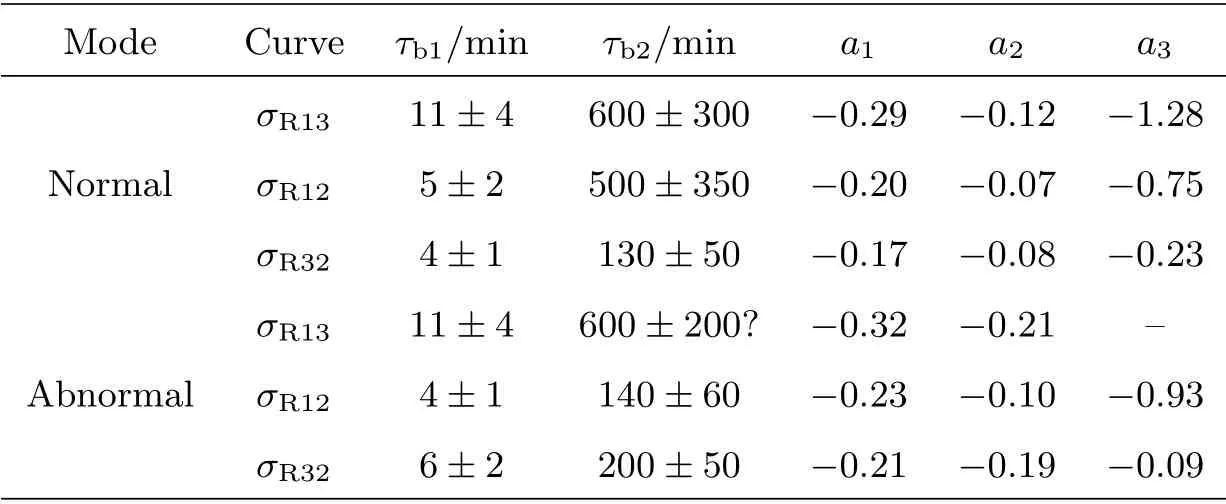
表2 基于20 d数据的lg σR−lg t曲线的分段线性回归参数.其中τb1和τb2表示曲线的拐点时标, a1、a2和a3表示曲线在3段时间区域上拟合得到的斜率. σR13、σR12和σR32的定义见正文.Table 2 The best-fit coefficients of linear regression for the lg σR−lg τ curves based on the 20-day observation. τb1 and τb2 are the turning time intervals of curves. a1, a2 and a3 are the slope rates fitted by the curves in three time segments.See text for the definition of σR13, σR12 and σR32.

为了对σR−τ的误差进行分析,我们从20 d的准连续数据中挑选出连续观测时间较长的4段正常模式(持续时间分别为15、9.2、9、9 h)和3段反常模式的数据(持续时间分别为3、2.5、2 h),用了和上面相同的方法对这些分段的数据进行处理,得到了分段数据的σR−τ曲线,如图4所示.图中黑色的线表示由20 d准连续数据得到的σR−τ曲线,正常模式的红色、蓝色、绿色和青色分别表示由4段分段的数据得到的σR−τ曲线,反常模式的红色、蓝色和绿色分别表示由3段分段的数据得到的σR−τ曲线.对比20 d连续数据和分段数据,我们发现,无论正常模式还是反常模式,由两部分数据得到的σR13、σR12和σR32曲线的整体趋势基本一致,但是在同样的积分时间上,σR的具体数值有一定的偏差.

我们由每个积分时间上σR偏差的最大值,定出对应σR值的误差范围,如图4所示,紫色的线表示我们根据上述方法得到的σR值的误差.σR产生误差的原因主要是由于以下两方面的因素造成的:(1)观测噪声的影响.由于有些轮廓的信噪比不是太高,观测轮廓信号窗口之外存在噪声信号,这会影响到轮廓信号窗口中每个成分的强度值,在求成分强度比时会带来误差.(2)观测采样点间隔bin造成的误差.我们所用的数据来自于2004年新疆南山望远镜的AFB (Analogue Filter Bank)终端,当时由于观测条件限制,采样率较低,每个积分轮廓在一个周期上仅有256个bin (近些年的观测数据每个周期上一般有1024个bin甚至更多),这样每个积分轮廓的每个成分上仅有5–6个bin,那么在求轮廓的不同成分的积分强度时必然会带来误差,就会给σR的值带来误差.

通过上述对比可以做出以下几点推断.(1)根据σR曲线和1−ρ曲线相似性可以对轮廓相关系数与各成分贡献的关系做出判断.对于正常模式,成分II和III的涨落是影响轮廓相关系数曲线或者说是影响轮廓形状趋稳行为的主要因素.对于反常模式,成分I和II的涨落是影响轮廓趋稳行为的主要因素.这两点和图1轮廓中3个成分的相对强弱关系是吻合的,说明确实是较强的成分对相关系数贡献较大,但这也间接地说明了较弱成分的强度涨落幅度并没有远超较强成分.我们发现无论对于正常模式还是反常模式,都是较强成分对相关系数的贡献较大,这有可能是因为较强的成分由于信噪比高更容易在较短的时标上形成强相关性,而较弱的成分则可能需要更长的时标才能形成较强的相关性,我们将在进一步的工作中通过数值模拟来探讨这种可能性;(2)3种σR曲线斜率变化的不同表明3个成分强度的涨落方式不同;(3)3种σR曲线都表现出在中等时标上的稳定速率放缓,拐折的时标和相关系数曲线定出的时标在量级上吻合,因此选用相关系数曲线斜率放缓的拐折点做为稳定性时标有代表性;(4)曲线的3段幂律特征表明很可能存在不同的因素导致轮廓不稳定性,这些因素起主导作用的时标不同.短时标的不稳定性很可能由辐射过程中脉冲强度的随机涨落主导,当积分时间达到几分钟以上时,短时标不稳定因素得到有效的抑制,中等时标上的不稳定因素开始显露出来,它引起的涨落超过了短时标因素.当积分时间达到几百分钟时,中等时标的不稳定因素导致的涨落应截止或迅速衰减,长时标的不稳定因素开始起作用.也就是说,从第2个拐折斜率增加的现象来推断,中等时标因素起作用的时间范围可能有上限,而长时标因素起作用的时间范围可能有一个下限.

4 讨论

上述分析只是从数据的时标特征出发,回答了为什么轮廓趋稳行为在不同时标上有明显差异.需要指出的是,R(t)时间序列是将许多段正常模式或者反常模式的子积分序列按时间顺序拼接而成的,并非天然的时间序列.但是有两点理由使我们认为上述趋稳行为在不同时间尺度上变化是可信的:(1)根据Chen等人2011年的结果,正常模式和反常模式窗口长度(持续时间)是随机的,服从伽马分布[7],不应导致R在中等时间尺度上的较规则的起伏.(2)跨度为7 yr的90次非连续观测和20 d的准连续观测的数据都显示相同的现象,排除了由于单次连续观测可能带来的问题.

这种差异性既可能是内禀的,由脉冲星辐射造成的,也可能是外源的,由观测噪声和星际闪烁等的影响导致.通过对模拟的噪声信号用同样的方法进行分析,我们排除了观测噪声的的影响.我们再讨论一下星际闪烁效应可能的影响.由于星际介质闪烁会影响到脉冲星的色散量,而脉冲星的色散会导致脉冲星在不同频率上接收到的信号有时间延迟,这样就会导致脉冲星平均轮廓的展宽和轮廓形状的不规则变化,从而影响轮廓的稳定性时标.这在一些脉冲星不同频率上的观测已经得到了验证,如PSR B0531+21和PSR B0833−45等[19].以前的观测表明,PSR B0329+54存在着折射式闪烁和衍射式闪烁现象,在1540 MHz上,这颗源动态谱上条纹频率漂移的折射式时标大约在(8±2)h,即360–600 min左右[20],而衍射闪烁的退相关时标为(595±50)s,大约10 min,退相关频率尺度为13 MHz左右[21].考虑到这两个时标和σR−t曲线上趋稳行为发生拐折的两个时段比较吻合以及频域上的窄频特征,我们推测星际闪烁可能是导致轮廓趋稳速率在中等时标上变缓的原因之一.根据Kramer等人对该星正常模式不同成分谱的研究,成分I、II和III的谱指数分别为−2.4±0.2、−2.4±0.2和−2.6±0.2[17].新疆天文台观测频率在1380–1700 MHz之间,理论上估算,如果两个时段中的闪烁分别导致1400 MHz和1700 MHz上的信号增强,即它们的子积分轮廓分别由这两个频率主导,那么这两个轮廓的I和III成分强度比值的差别最大可达到12%((1400/1700)−2.2+2.8−1).以正常模式为例,R的平均值约为0.55,星际闪烁效应理论上可以使R值在0.48到0.62之间变化.当然,实际的正常模式R值涨落范围在0.3到0.8之间,因此应该还有其他因素的贡献.

对R的涨落有贡献的另一个因素是在子积分时间内模式发生变化,从而导致子积分轮廓是两种模式的混合.但是正常模式特征持续时标约为154 min,而反常模式特征持续时标仅有31.5 min[7],两者差距很大,因此这个因素难以解释为什么正、反模式轮廓趋稳行为的变化都发生在接近的时间拐点.脉冲星辐射的内禀因素也是可能的,不过对这一点的推断需要建立在更深入的研究基础上.

5 总结与展望

本文利用新疆天文台25 m射电望远镜450 h以上的历史观测数据,研究了PSR B0329+54的两种模式在1540 MHz上的累积脉冲轮廓的稳定性.通过考察不同积分时间上的积分脉冲轮廓与参考轮廓的交叉相关系数,发现两种模式的相关系数曲线都在短、中、长积分时标上呈现出不同的变化趋势,反映出随着积分时间的增加,脉冲轮廓趋于稳定的速度经历由快到慢再到快的转变.对正常模式而言,趋稳速度发生拐折的积分时间段为(4±1)min和(140±60)min;对反常模式,拐折时段为(4±1)min和(65±15)min.我们认为把趋稳速度由快过渡到慢所需要的积分时间作为轮廓形状的稳定性时标比较合理,由此定出两种模式的趋稳时标大约都是5 min.和HTM75相比,我们在确定稳定时标的方法和结果上都有所不同.

本文也考察了轮廓中3个不同相位段上成分的稳定性行为,方法是计算不同积分时间上每两个成分强度比值的涨落水平,并检查它随积分时间的变化.结果表明,这3个成分的趋稳行为和轮廓整体上的趋稳行为类似,但3个成分强度的涨落方式有所不同.我们初步探讨了造成中等时标和长时标上趋稳速度拐折的可能原因,例如星际闪烁等.本文结果对研究射电脉冲辐射中的随机过程、星际闪烁以及脉冲星到达时间等问题都有一定的参考价值.

致谢感谢新疆天文台脉冲星小组成员对本论文提供的帮助.