一种基于损伤等效原理的PSD路谱生成方法

王玮，周肖飞，陈文斐，翟云飞

(1. 西安交通工程学院，陕西 西安710300；2. 陕西汽车控股集团有限公司，陕西 西安710200)

0 引言

在车辆耐久分析中，往往通过静力学分析求解单位载荷作用下的结构响应，叠加道路载荷谱后形成应力时间历程曲线求解疲劳寿命。这种方法简单直接，得到了大量的应用[1]。也有将载荷谱直接加载到分析部件上，求解瞬态动力学响应，以考察结构的动态特性对疲劳的影响，使疲劳结果更接近真实[2]。但采用瞬态方法往往带来更多的计算量，在工程中需要一种能够保证精度且更快速的分析手段。

在结构安装位置处布置加速度传感器获取载荷激励，通过傅里叶变换(FFT)转换为功率谱密度曲线(PSD)，然后通过随机响应分析估算结构的应力范围，进而计算结构的疲劳寿命[1]。这种方法计算效率较高，精度满足需求，故而被广泛应用。但随着车辆耐久试验的复杂化，每次试验往往包含多种路面工况，由于不同路面的激励频率和幅值都有所不同，该随机过程无法用平稳过程描述。因此在进行傅里叶变换时会对PSD幅值进行平均。

图1为一个典型的车辆耐久试验路谱，其中搓板路激励的时间较长，频率较低，幅值较小，而比利时路面激励的时间极短，频率较高，幅值极大。在这种情况下，直接的傅里叶变换会导致搓板路激励和比利时路激励在相同频率时出现幅值平均，从而导致最终的损伤值偏低。

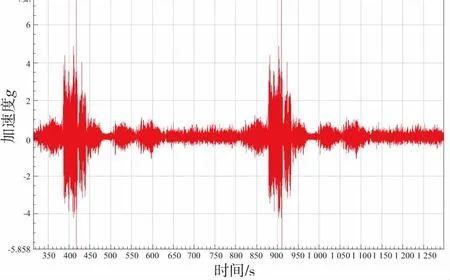
图1 某路试加速度谱

本文提出了采用损伤等效原则的PSD生成方案，实现转换前后载荷幅值和频率的一致，为解决复杂路面激励提供了一种解决方案。

1 基于FDS的PSD生成方案

1.1 处理流程

基于FDS的PSD生成，就是通过原始载荷谱计算损伤谱，再由损伤谱转换为PSD谱。在转换过程中必须遵守两个原则：第一，必须保证转换前后对结构造成的疲劳损伤是一致的；第二，必须保证在转换前后载荷的幅值是相同的。其转换流程如图2所示。

图2 基于FDS的PSD谱生成流程

1.2 冲击响应谱

1932年，美国工程师Biot通过研究地震对相关结构的损伤时发现：单自由度振子系统的响应由其自然频率主导，低于自然频率的部分表现为准静态效应；超出自然频率的部分随着激励频率的增加会逐渐减弱；在自然频率附近，结构的振动幅值会大幅度增加。此时，其幅值大小由系统阻尼决定，动态响应与静态响应的比值称之为幅值比Q，当阻尼为0.05时，幅值比Q=10[3]，如图3所示。

图3 激励频率与加速度响应的关系

将时域载荷谱与该频率响应函数相乘，得到在当前自然频率下的时域响应信号。采集该响应信号的最大值，可描绘出结构最大响应与自然频率之间的关系曲线(此时只为一个点)，即为单自由度振子系统的响应谱曲线(response spectrum, RS)

将其推广到多自由度系统上，由于多自由度系统具有多个自然频率，就需要重复上述分析过程，分别计算载荷谱在不同自然频率下的最大响应，将所有的最大响应点相连，可获得多自由度系统最大响应与频率的关系，即为冲击响应谱(shock response spectrum，SRS)。其计算流程如图4所示。

图4 冲击响应谱获取流程

1.3 损伤谱的获取

受冲击响应谱的启发，Halfpenny提出了利用时域信号计算损伤谱的方法，将各个频率下的结构响应通过雨流计数统计，直接加载到S-N曲线上，可获得载荷在各个频率下的损伤值。在获得某个自然频率下的时域响应曲线后，直接用该响应曲线进行雨流统计，然后计算其累计损伤，即可得出损伤谱(fatigue damage spectrum，FDS)[4]，如图5所示。

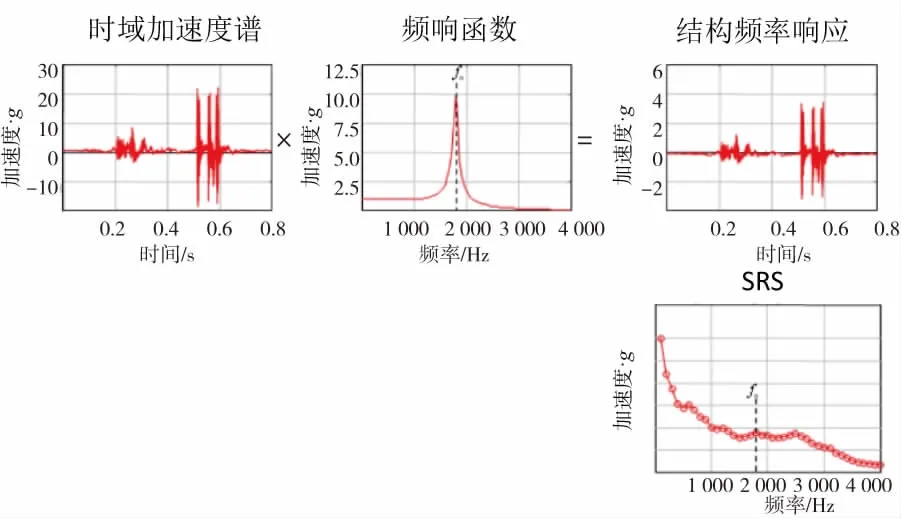
图5 损伤谱获取流程

其方法分为4个步骤：

1)将激励信号加载在单自由度系统上，计算在某个自然频率下的载荷时间历程；

2)对该载荷时间历程进行雨流计数，计算该频率下的累计损伤；

3)多次重复前两步操作，计算多个频率下的累计损伤；

4)将损伤与频率描绘在平面坐标系中，即为损伤谱。

损伤谱可以清晰地表达出在某个频率下载荷对结构产生的损伤值大小，可以更准确地反映出载荷对结构的破坏能力。

1.4 极端响应谱

对于时域载荷而言，冲击响应谱能够清晰地给出结构最大响应与频率的关系，但在实际中，很多载荷都是随机性的，使用PSD谱表达载荷分布更为准确。如何用类似与SRS的方式简单地表达出结构的最大响应，1953年，Miles给出了结构响应的均方根值(RMS)与频率的关系式[5]，假设激励为高斯分布，则对于加速度而言

(1)

对于位移而言

(2)

其中：Q为幅值比；fn为结构的自然频率。

1978年，Lalanne通过统计发现，对于窄带的激励而言，其激励分布更偏向于瑞利分布(rayleigh)，故需要将上式进行修正[6]，修正后的方程如式(3)和式(4)所示，对于加速度而言

(3)

对于位移而言

(4)

此即为极端响应谱(extreme response spectrum, ERS)。

1.5 极端响应谱的损伤曲线估计

2002年，Lalanne基于极端响应谱的估计，提出了基于ERS的损伤曲线方程，使得可以直接从PSD曲线中获取FDS[7]，其结构如下：

(5)

其中：fn为结构自然频率；K为结构刚度；C和b为材料疲劳参数；Γ为伽马方程，其具体形式为

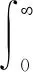
(6)

1.6 基于FDS的随机谱合成

式(3)表示由PSD谱计算极端响应谱的过程，式(5)表示极端响应谱和损伤谱的关系，将两方程进行反推，即可获得从损伤谱计算极端响应谱的方法。而损伤谱可直接将时域载荷谱通过雨流计数获取。如此，就打通了从时域谱如何获取PSD谱的全过程，但在这个流程中，需要考虑安全因子的影响。

安全因子可用载荷大小与材料疲劳强度的比值来表达：

(7)

实际工程中，施加在结构上载荷往往表现出明显的随机性，由于材料的疲劳性能同样存在随机性，因此安全因子不仅要考虑载荷大小和疲劳强度，同时还需要考虑存活率的影响。

图6中，x轴表示应力大小，y轴表示出现概率。假设随机载荷和材料疲劳强度均呈现高斯分布，那么两条概率分布曲线的重合区域即为结构在该随机载荷作用下的失效率，非重合区域则为存活率。显然两者存在以下关系：失效率+存活率=1。

图6 材料的失效率

对于高斯分布，安全因子与存活率可用下式表达：

(8)

其中：a′表示存活率；VR表示强度变化率；VE表示载荷变化率，其可用下式表达：

(9)

(10)

其中σR和σE分别是材料疲劳强度和载荷的标准差。

将式(5)反推并考虑安全因子的影响，可获得从FDS求解PSD的方程

(11)

2 基于FDS的PSD随机疲劳分析

某商用车电瓶箱结构如图7所示。

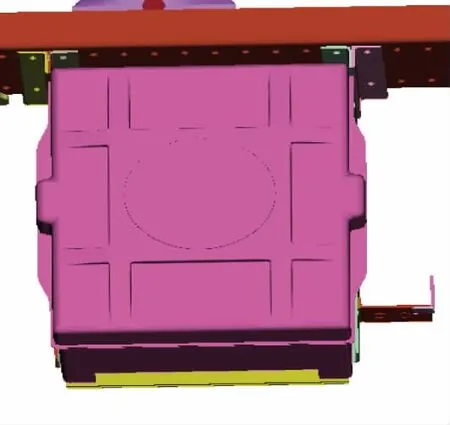
图7 某商用车电瓶箱示意图

在约束位置加载幅值为1g的正弦波，计算频率从1Hz～200Hz的扫频响应。图8为521号单元在3个方向的频率响应曲线。

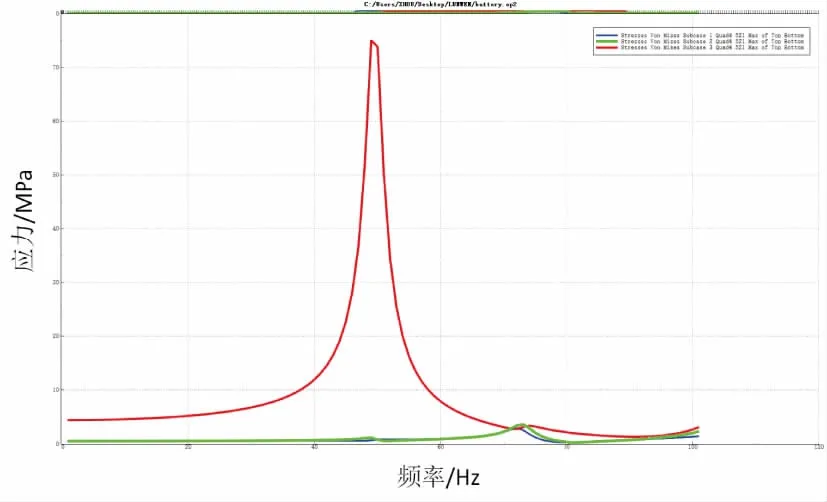
图8 单元应力频响曲线

在电池包根部粘贴加速度传感器，采集到根部的加速度载荷如图9所示。

图9 电瓶箱根部的加速度谱

由于路谱具有很强的随机性，因此常采用随机振动的方式计算结构响应。对x方向的谱分别采用直接转换的方式和FDS转换的方式转成PSD谱，如图10所示。

图10 两种方式生成的PSD谱

可以看出，由于存在幅值的平均，采用傅里叶变换直接生成PSD谱的最大值明显被削弱了，采用FDS转换的方式计算出来的PSD谱在低频段(3Hz以内)偏小，而在高频段(10Hz以上)偏大，这是由于路谱在低频段能量偏低但时间较长，在高频段能量较大但时间偏短造成的。

在疲劳分析软件中，分别加载直接转换的PSD谱和采用本文方法转换的PSD谱计算结构的疲劳寿命，结果如图11所示。

图11 两种载荷下电池包的寿命云图

由图11可知，采用两种PSD谱计算的寿命分布趋势基本一致，但量级上存在较大差异，采用直接转换PSD谱计算的最小寿命为5.2×106次循环，采用本文方法计算的电池包寿命为2003次循环。鉴于该最小寿命往往出现在约束周边的应力集中位置，真实结果应大于最小寿命，对结构重点部位寿命进行采集，与试验结果对比如表1所示。

表1 计算结果与试验结果对比 单位：次

由表1可知，采用本文方法转换的PSD谱在结构上产生的损伤要远大于直接转换PSD谱的损伤，与实际试验结果也比较吻合。

3 结语

在工程实际中，大多数路试路谱都很复杂，而且呈现出明显的随机性，采用传统方法计算疲劳寿命需要对路谱进行分割，单独计算各路段的三向损伤，然后将损伤进行线性叠加，这带来了巨大的工作量。通过FDS进行PSD谱的转换，可以大幅度缩减重复工作，并且保证转换前后损伤的统一，对工程应用有很大的帮助。