超声空化对陶瓷刀具材料晶粒生长的影响

李东绪，宋金鹏✉，高姣姣，吕 明

1)太原理工大学机械与运载工程学院，太原 030024

2)太原理工大学精密加工山西省重点实验室，太原 030024

化晶粒、加速合金固溶以及改善材料力学性能的效果[2-3]。然而，有关超声辅助无压烧结陶瓷刀具材料的相关研究较少，超声波的空化效应对陶瓷刀具材料晶粒生长的影响机制尚不明确。采用蒙特卡罗法可实现对晶粒生长过程的模拟，刘曦阳[4]利用蒙超声技术是20世纪发展起来的一种高新技术，目前主要应用在超声治疗、超声焊接、超声清洗和超声分散等领域[1]。国内外学者研究了超声波对铝熔体和铝合金组织的影响，发现超声波可在金属熔体中引发空化效应，从而达到增大熔体形核率、细特卡罗法模拟了Al2O3/SiC陶瓷刀具材料微观组织的演变过程。王晓勉等[5]利用蒙特卡罗法进行了粉末固相烧结的晶粒生长动力学模拟。邵想等[6]采用蒙特卡罗法模拟了不含气孔的Mo2FeB2基金属陶瓷材料在液相烧结阶段的微观组织演变过程。但是，将蒙特卡罗法用来模拟超声辅助无压烧结下晶粒生长的研究较少。因此，本文从超声理论和陶瓷刀具材料的液相烧结理论出发，构建超声作用下无压烧结陶瓷刀具材料时晶粒生长的模型，研究超声空化效应；同时，利用蒙特卡罗法模拟超声作用下无压烧结陶瓷刀具材料时晶粒的生长过程。

1 材料及理论

1.1 材料的选用

由功率超声处理金属熔体的相关研究可知，金属熔体中存在的气泡在一定的超声作用下可发生空化效应[2]。而在陶瓷刀具材料的制备过程中，常通过加入金属相来改善陶瓷相的可烧结性，提高材料的相对密度和综合力学性能。因此，在陶瓷刀具材料的烧结过程中，当烧结温度高于金属相的熔点且材料致密化不完全时，烧结体中将存在熔融金属和气泡，这是实现超声空化的介质基础。

TiB2是一种优秀的耐高温陶瓷材料，在高温条件下，TiB2与钢的附着力较低，这使其在高速切削领域有较好的发展前景。在TiB2陶瓷刀具材料的制备过程中，常选用Ni或Al等金属作为烧结助剂，而金属Ni对TiB2的润湿性更好，且经济性更高[7]。因此，本文以无压烧结制备含金属Ni的TiB2陶瓷刀具材料为例，对超声作用下陶瓷刀具材料的晶粒生长过程进行分析。

1.2 超声空化的相关理论方程

在材料的制备过程中加入超声波作用后，要在液相中实现超声空化效应，必须打破气泡的平衡态，打破气泡平衡态所需要的最小声压称为声压阈值，用Pt来表示，如式（1）所示[8]。

式中：σ是熔体表面张力，N·m−1；P0是熔体的静压力，Pa；R0是气泡的初始半径，m；Pt是声压阈值，Pa。

在超声波的作用下，液相中的气泡会不断地压缩或膨胀，当气泡共振频率大于超声频率时，气泡会发生振动并产生空化效应[9]，因此在气泡产生空化效应时，超声波能够达到的最大值为频率阈值，频率阈值通常由气泡的共振频率来表示，其计算式如式（2）所示[10]。

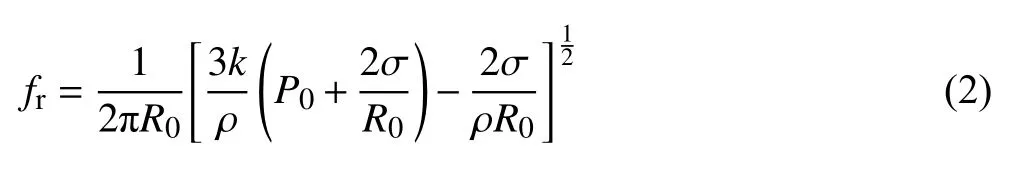
式中：fr是气泡共振频率，Hz；R0是气泡初始半径，m；k是气体多边指数；ρ是熔体密度，kg·m−3；P0是熔体的静压力，Pa；σ是熔体的表面张力，N·m−1。

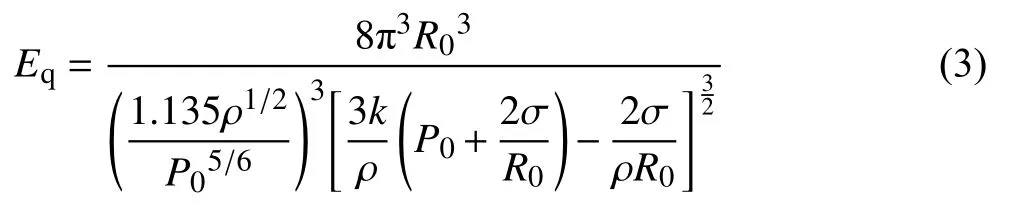
在超声作用下，气泡发生空化时所释放的能量用气泡脉动能（Eq）来表示，其计算式如式（3）所示[11]。式中：R0是空化泡初始半径，m；k是气体多边指数；ρ是熔体密度，kg·m−3；P0是熔体的静压力，Pa；σ是熔体的表面张力，N·m−1；Eq是气泡脉动能，J。

2 超声空化理论分析

2.1 气泡声压阈值和频率阈值的数值分析

由式（1）分析可得图1所示的气泡初始半径与声压阈值的关系。由图可知，当气泡处于温度为1600 ℃的熔融金属Ni中，熔体静压力为P0=1.013×105Pa，熔体表面张力为σ=1.75 N·m−1。

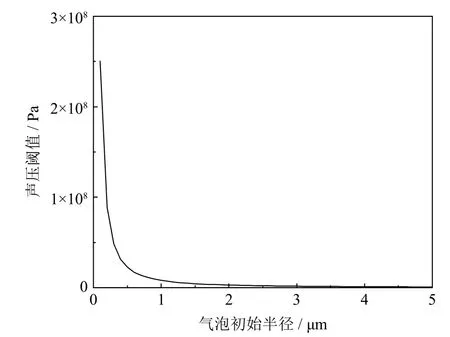
图1 气泡初始半径与声压阈值的关系Fig.1 Relationship between the initial radius of the bubbles and the threshold of sound pressure

由图1可知，气泡的初始半径越小，气泡空化所需要的声压阈值就越大。在气泡初始半径由0 μm增加到1 μm的过程中，声压阈值大幅度减小；当气泡初始半径大于2 μm时，随着气泡初始半径的持续增大，声压阈值缓慢减小并趋于0 Pa。本文所选气泡的初始半径介于1 μm～2 μm，在此范围内选取气泡初始半径所对应的最大声压阈值为8.02×106Pa。

由式（2）分析可得图2所示的气泡初始半径与频率阈值的关系。由图可知，气泡在1600 ℃的熔融金属Ni中，熔体表面张力为1.75 N·m−1，气体多边指数为1.33，熔体的密度为8902 kg·m−3。

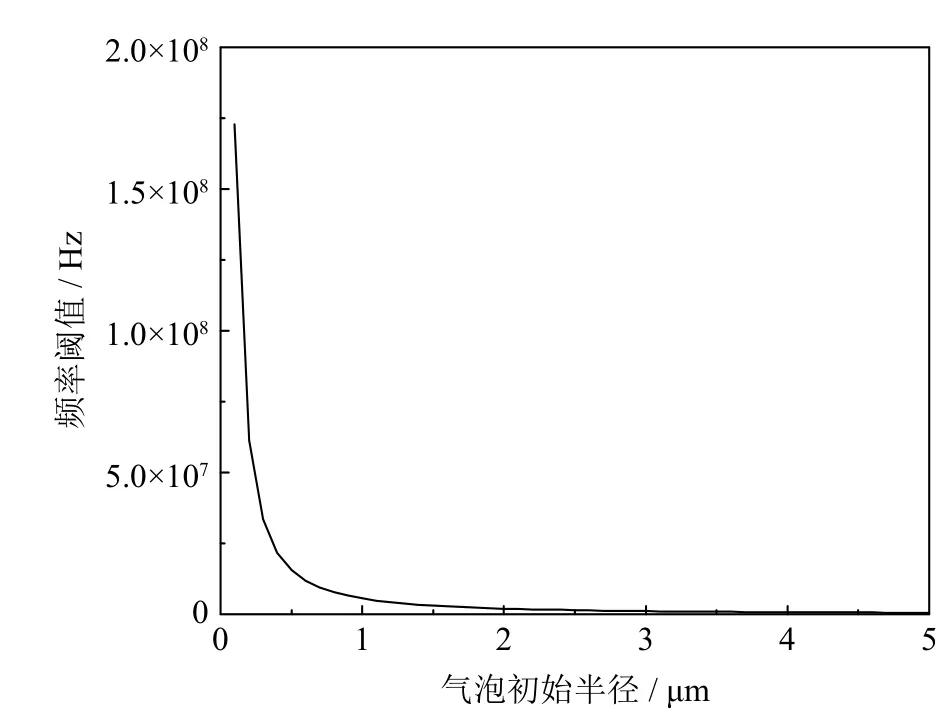
图2 气泡初始半径与频率阈值的关系Fig.2 Relationship between the initial radius of the bubbles and the threshold frequency

由图2可知，在气泡初始半径由0 μm逐渐增大到1 μm的过程中，频率阈值大幅度减小；随着气泡初始半径的进一步增大，频率阈值减小速度变得缓慢。本文所选取的气泡半径介于1 μm～2 μm，由于气泡实现空化所需的频率要小于气泡的共振频率，因此在选取的气泡半径范围内选取其对应的最小频率阈值，即气泡初始半径为2 μm时的频率阈值2.00×106Hz。

在TiB2陶瓷刀具材料的无压烧结过程中施加超声波后，当超声波的声压阈值为8.02×106Pa、频率阈值为2.00×106Hz时，材料中半径为1 μm～2 μm的气泡可在熔融金属Ni中发生超声空化。空化效应作为超声波在液体介质中的独特现象，可在介质中引发瞬时的高温和高压、微射流以及冲击波等作用[12]，当气泡发生空化时，这些作用将影响气泡周围晶粒的形核与长大，发生空化效应的气泡称为空化泡。

2.2 空化泡对晶粒的作用

在理想状态下，假设陶瓷材料液相烧结阶段时的晶粒与空化泡都是球体，一个空化泡周围有多个晶粒，且空化泡与晶粒、晶粒与晶粒之间都是紧密接触，金属液相填充在晶粒与空化泡的周围，据此构建空化泡及其周围晶粒的理想模型，如图3所示。此简化模型的建立并非以TiB2陶瓷刀具材料的性质为依据，在满足材料中同时含有固相、液相和气相的条件下，此模型可分析空化泡对不同陶瓷材料晶粒的作用。

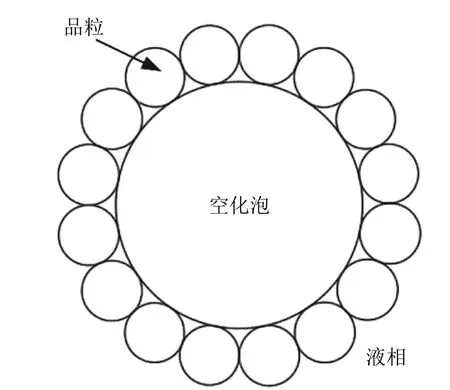
图3 空化泡及其周围晶粒的理想模型Fig.3 Ideal model of the cavitation bubbles and surrounding grains

在含有金属相Ni的TiB2陶瓷刀具材料无压烧结过程中施加超声波，当材料中气泡初始半径为1 μm时，由式（3）可知，气泡脉动能Eq约为1.54×10−14J，即1 μm的气泡发生空化时释放的能量约为1.54×10−14J。

在图3中，设定晶粒半径r=0.25 μm，气泡半径为R0=1 μm，则空化泡周围晶粒的数量（N）如式（4）所示。

式中：N是空化泡周围的晶粒数量。

空化泡周围单个晶粒吸收的空化能如式（5）所示。

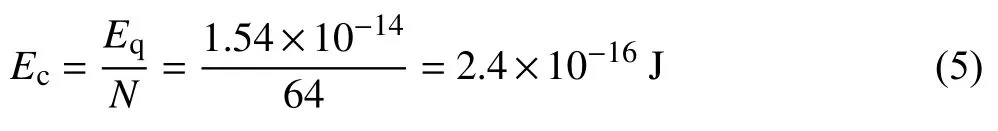
式中，Ec是空化泡周围单个晶粒吸收的空化能，J。

一个半径为0.25 μm的晶粒中所包含的分子个数如式（6）所示。

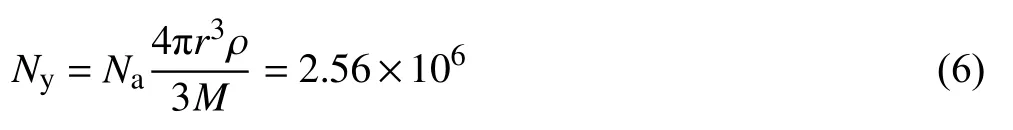
式中：Na是阿伏伽德罗常数；Ny是晶粒中所包含的分子个数；M是TiB2分子的摩尔质量，kg·mol−1；ρ是陶瓷材料TiB2的密度，kg·m−3。

因此，单个分子吸收的空化能如式（7）所示。

式中：Ey是单个分子吸收的空化能，J。

由晶态固体热容的量子理论可知，质点振动能量与质点振动频率有关，其关系如式（8）所示。

式中：v是质点振动频率，Hz；h是普朗克常数，J·s；E是质点平均振动能量，J；kB是玻尔兹曼常数，J·K−1；T是温度，K。

由文献[13]可知，当陶瓷材料不受超声作用时，质点的最大振动频率约为v0=9.55×1012Hz，由式（8）可知此时质点的振动能量为E0=2.592131×10−20J，当施加超声后，质点的振动能量如式（9）所示。

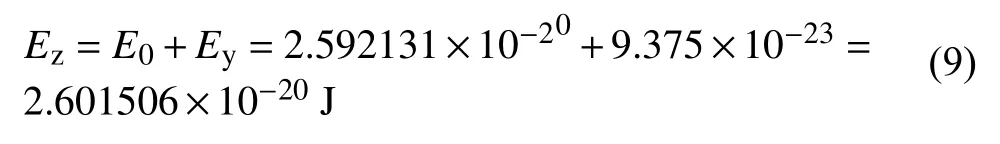
将质点的振动能量Ez代入式（8）可得质点的振动频率约为v1=1.27×1013Hz。由此可知，施加超声作用后，晶体点阵中的质点振动频率和振动能量都将增大，因此晶格振动频率也将增大，晶格振动频率越高，枝晶会因振动而破碎形成新的晶核，可提高形核率，达到细化晶粒的作用。

3 蒙特卡罗模拟

3.1 模拟模型的建立

在陶瓷材料的无压烧结过程中，晶粒的生长直接影响着材料的微观结构及力学性能，国内外学者采用多种方法模拟了陶瓷材料烧结过程中的微观组织演变过程，并研究了不同的烧结参数对晶粒生长的影响[14]。与相场法和元胞自动机相比，蒙特卡罗法作为一种计算量较小，模拟效率较高的模拟方法，常被用来模拟晶粒的生长过程[15]。基于此，本文使用Matlab软件，采用蒙特卡罗法模拟了超声作用下无压烧结TiB2陶瓷刀具材料的晶粒生长过程。

在Matlab软件中，将200×200 μm2的陶瓷材料微观组织映射到400×400的二维点阵中。对每个格点进行赋值，以确定各格点的取向值，固相格点的取向值介于1～Q，气孔格点的取向值为−1，液相格点的取向值为Q+1。有研究表明Q的取值应大于32，本次模拟取Q为60[16]。固相格点中相邻且取向值相同的格点构成一个固相点阵单元，表示一个晶粒，相邻且取向值不同的格点之间形成晶界；相邻且取向值为−1的格点构成气孔；相邻且取向值为Q+1的格点构成连续的液相。在对格点赋值时，将10%的格点设为液相格点，以表示陶瓷材料中含有10%的液相；将26%的格点设为气孔格点，以表示陶瓷材料的初始气孔率为26%；其余格点为固相，代表陶瓷相的含量。

在进行蒙特卡罗模拟时，以各相的任一格点为起点，任一格点及其邻近各格点组成一个小的模拟单元，在每个小的模拟单元中都可能含有固、液和气三相，因此模拟单元中可能含有的能量为固相间的晶界能、固-液界面能、固-气界面能和液-气界面能，其总能量可表示如式（10）～式（14）所示。

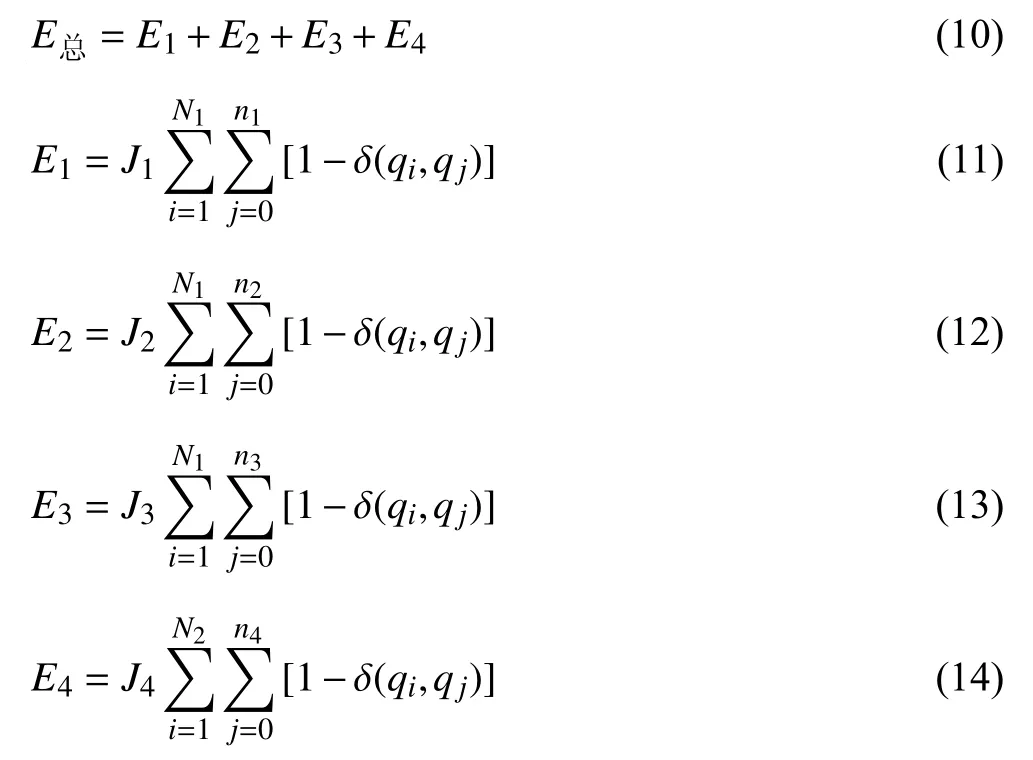
式中：E总是一个模拟单元的总能量，J；E1是模拟单元中固相间的晶界能，J；E2是模拟单元中的固-液界面能，J；E3是模拟单元中的固-气界面能，J；E4是模拟单元中的液-气界面能，J；J1是固相间的单位晶界能，J；J2是固-液单位界面能，J；J3是固-气单位界面能，J；J4是液-气单位界面能，J；N1是模拟系统中固相的格点数；N2是模拟系统中液相的格点数；n1是某一固相格点相邻的固相格点数；n2是某一固相格点相邻的液相格点数；n3是某一固相格点相邻的气相格点数；n4是某一液相格点相邻的气相格点数；δ(qi,qj)是克罗内克函数，当qi=qj时，δ(qi,qj)=1，当qi≠qj时，δ(qi,qj)=0。

在本模拟中，引入温度和超声波的影响因子以体现温度和超声波对晶粒生长的影响，其中，温度影响因子用KT表示，如式（15）所示[4]。

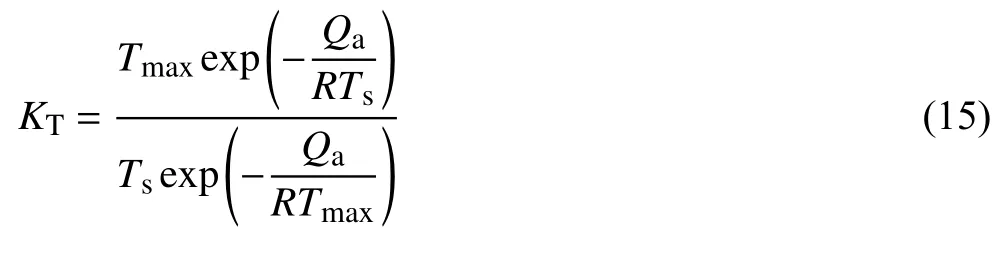
式中：Tmax是烧结过程的最高温度，K；Ts是绝对温度，K；Qa是激活能，J；R是气体常数。

由于蒙特卡罗法是将材料微观组织映射为点阵，通过对点阵赋值以模拟晶界的迁移过程，而超声空化能够增大晶格振动频率与振动能量，引起枝晶破碎，提高形核率，为此引入超声影响因子（K）表示超声对物质迁移速率的影响，其计算式如式（16）所示。

式中：v0是未施加超声时的质点振动频率，Hz；v1是施加超声后的质点振动频率，Hz。

此外，在模拟中还需用到晶粒重取向概率（P），其计算式如式（17）所示[6]。

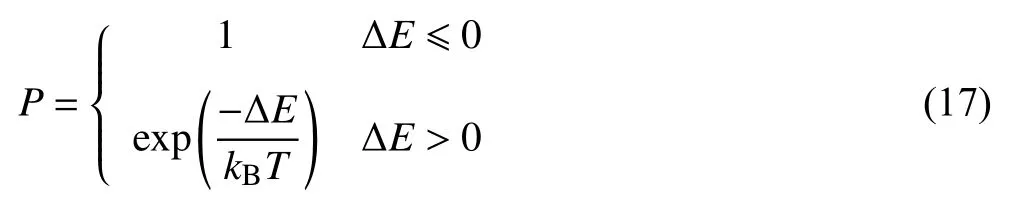
式中：ΔE是对格点尝试再取向造成的能量差，J；kB是玻尔兹曼常数；T是温度，K。

将超声影响因子、晶粒重取向概率和温度影响因子相乘，可得超声和温度共同作用下的晶粒重取向概率，本次模拟中的烧结温度为1600 ℃。

3.2 模拟算法

在确定了点阵模型、系统能量构成以及晶粒重取向概率后，即可采用蒙特卡罗法并利用Matlab软件对晶粒的生长过程进行模拟，具体模拟流程如下：

（1）在点阵中随机选取一个格点，若此格点位于某相的点阵单元内部，则重新选取格点，直到所选取的格点位于点阵单元的边界上。

（2）若上述所选格点为固相格点，则据式 （10）计算重取向前的固相格点与相邻各格点间的能量和。

（3）若在点阵单元边界处选取的格点为固相格点，则判断其邻近格点中是否存在连续的4个气孔格点。若被选固相格点的邻近格点中存在4个连续的气孔格点，即固相晶粒周围存在空化泡，则从1−Q中任取一值q，并将被选固相格点的取向值替换为q，实现被选固相格点的重取向；然后，据式（10）计算重取向后的固相格点与相邻各格点间的能量和，可知重取向前后固相格点与相邻各格点间的能量变化量（ΔE总），将ΔE总带入式（17）可知P值；用随机函数生成一个介于0～1的随机数ξ，判断KKTP>ξ是否成立，若成立则执行被选固相格点的重取向，此过程将模拟半径为1 μm的气泡发生空化作用、增大形核率的作用，若不成立则重新选取格点。若被选固相格点的邻近格点中不存在4个连续的气孔格点，但存在某一固相格点M，且其取向值与被选固相格点不同，则用格点M的取向值替换被选固相格点的取向值，实现被选固相格点的重取向；据式（9）计算重取向后被选固相格点与相邻各格点间的能量和，可知重取向前后固相格点与相邻各格点间的能量变化量（ΔE总），将ΔE总带入式（17）可知P的值；用随机函数生成一个介于0～1的随机数ξ，判断KTP>ξ是否成立，若成立则执行被选固相格点的重取向，此过程将模拟晶粒的正常生长，若不成立则重新选取格点。

（4）若在点阵单元边界处选取的格点为液相格点，则取其邻近最小和最大固相点阵单元，将最小固相点阵单元中与液相格点相邻的格点的取向值替换为液相格点的取向值，来模拟小晶粒在液相中的溶解过程；然后，将所选液相格点的取向值替换为最大固相点阵单元的取向值，从而模拟晶粒的析出过程。

（5）若在点阵单元边界处选取的格点为气孔格点，且其邻近格点中同时存在气孔格点和固相格点，则将被选气孔格点取向值与邻近固相格点的取向值进行交换，此过程模拟了气孔的迁移；若被选气孔格点的邻近格点中没有气孔格点，但存在固相格点，则用固相格点的取向值替换被选气相格点的取向值，并将气相格点的取向值赋予材料最外层边界上的固相格点，此过程在保证系统质量不变的情况下模拟了空位湮灭的过程。

以上是点阵模型中一个格点的模拟流程，由于本模拟的格点数为160000，因此重复运行160000次，可完成所有格点的选取，即完成一个蒙特卡罗模拟时间步，为了获得相对精确的模拟结果，本模拟设定蒙特卡罗模拟时间步为500。

3.3 模拟结果

图4是未施加超声与施加超声下模拟得到的陶瓷刀具材料最终晶粒形貌，其中，白色的小点是液相，黑色相为气孔，其余为固相晶粒。由图可见，经过相同的蒙特卡罗模拟时间步（500）后，材料内部的大部分气相通过气孔迁移和空位湮灭逸出到材料外部；与未施加超声的模拟结果相比，施加超声下的陶瓷刀具材料晶粒较小，气孔较小且大气孔较少，这表明施加超声有助于细化晶粒、减小孔洞。

图4 蒙特卡罗法模拟的陶瓷刀具材料晶粒形貌：（a）未施加超声；（b）施加超声下Fig.4 Grain morphology of the ceramic tool materials simulated by the Monte Carlo method: (a)without ultrasound;(b)with ultrasound

为了更好地揭示超声对晶粒大小的影响，本文计算了晶粒平均半径，其计算方法为：首先假设晶粒大小相等且为圆形，然后依据蒙特卡罗模拟时间步所输出的晶粒总面积和晶粒个数，求出单个晶粒的面积和半径，此半径即为此模拟时间步下的晶粒平均半径。图5是未施加超声与施加超声下陶瓷刀具材料晶粒平均半径随模拟时间步变化的对比曲线。由图5可知，未施加或施加超声时，晶粒的平均半径都随着模拟时间步的延长而逐渐增大，模拟初期晶粒生长较快，模拟中后期晶粒的生长速度较慢并趋于稳定；在同一模拟时间步下，施加超声所获得的晶粒平均半径要小于未施加超声所获得的晶粒平均半径；在模拟时间步为500时，未施加超声和施加超声后的晶粒平均半径分别为3.78 μm和2.56 μm。这表明施加超声可降低晶粒的生长速度，达到减小晶粒尺寸的效果。

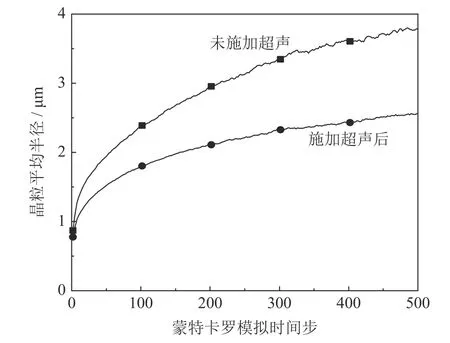
图5 陶瓷刀具材料晶粒平均半径与蒙特卡罗模拟时间步的关系Fig.5 Relationship between the grain average radius of the ceramic tool materials and the Monte-Carlo step

4 结论

（1）在含有金属相Ni的TiB2陶瓷刀具材料无压烧结过程中施加超声波，当超声波的声压阈值为8.02×106Pa、频率阈值为2.00×106Hz时，熔融金属中半径为1 μm～2 μm的气泡可发生超声空化。

（2）建立了空化泡及其邻近晶粒的理想模型，施加超声后，超声空化能够提高晶格的振动频率和振动能量，从而增大形核率，阻碍TiB2陶瓷刀具材料晶粒的生长。

（3）依据超声空化对TiB2晶粒生长的影响，采用蒙特卡罗法模拟了未施加和施加超声下的晶粒生长过程，模拟结果表明施加超声有助于减缓晶粒的生长速度、细化晶粒、减小孔洞。