风城油田齐古组油砂细观结构和渗流特征

庞惠文，金衍，高彦芳，王琪琪

（1.中国石油大学（北京）a.油气资源与探测国家重点实验室；b.理学院；c.石油工程学院，北京 102249；2.西北大学 地质学系，西安 710069）

稠油作为非常规油气资源的重要组成部分，是中国未来常规油气资源的有效接替[1]。中国西部和东北部地区稠油资源丰富，其中新疆准噶尔盆地风城油田稠油储量约为3.6×1012t[2]，开采潜力大，但平均黏度超过10 000 mPa·s（50 ℃），给高效开发带来巨大挑战[3]。蒸汽辅助重力泄油（SAGD）技术是中国目前常用的稠油开发技术，已广泛应用于包括风城油田在内的多个油田。风城油田上侏罗统齐古组砂岩储集层属于陆相河道沉积，具有非均质性强、泥质含量高、原油黏度大等特点，在应用SAGD 技术开采时，预热周期长，蒸汽能耗大。目前形成了以快速启动技术为代表的注水微压裂改造技术，即在循环注蒸汽前，先对储集层进行注水微压裂改造，以形成沟通注采井间均匀的高渗扩容带，为后期蒸汽腔的形成和发育提供有效通道[4]。但由于风城油田储集层孔隙结构和渗流规律复杂，导致部分井改造效果不理想，亟需针对油砂细观结构和渗流特征开展精细化研究，为微压裂改造方案的优化和稠油油藏的高效开发提供理论依据。

针对储集层细观结构和渗流特征的研究方法主要包括间接法、直接法和数字岩心重构3 类。研究区齐古组砂岩储集层结构疏松，易受外部扰动，若采用以光学显微镜和扫描电镜为主的定性或半定量细观结构分析方法，以及稳态和瞬态渗透率实验室测试方法，在制样和压力保持方面均存在很大困难[5]。因此，无损CT 配套重构分析技术成为定量表征油砂细观结构和渗流特征的有效途径，但准确区分岩心不同组分的颗粒接触方式、孔隙网络建模以及孔隙尺度流动模拟，是数字岩心技术面临的主要难题[6]。

构建数字岩心的基础是对二维岩心图像的处理和分析，针对CT 获得的图像，需要进行图像预处理和图像分割。图像预处理方法主要包括中值滤波、各向异性扩散滤波、全变差滤波、非局部滤波等[7]。图像分割方法主要包括全局阈值法、局部阈值自适应法、区域生长法、可变形表面水平集法、概率模糊聚类法、贝叶斯法和分水岭分割法[8]。数字岩心建模方法主要有物理实验法和数值重建法2 种，皆可以用来表征孔隙和基质的空间分布关系[9]。物理实验法通过对有序的岩心二维断层扫描，直接进行三维重构；数值重建法以少量二维图像为基础，运用特定数值方法构建数字岩心。在重构的数字岩心上，可以建立孔隙网络模型来分析孔隙连通情况，孔隙网络构建方法主要包括多向扫描法、居中轴线法、Voronoi 多面体法、最大球体积法等[10]，其中居中轴线法较为常用。开展孔隙尺度流动模拟的方法主要分为3 类：第一类是基于连续性假设的宏观尺度求解法，即依据经典力学理论，采用传统计算流体动力学直接求解Navier-Stokes 方程[11]；第二类是基于非连续假设的介观尺度求解法，即依据统计物理学理论，通过追踪粒子微团运动行为来描述流体流动特征[12]；第三类是基于非连续假设的微观尺度求解法，该方法依据统计物理学直接描述分子或原子的运动[13]。上述3种方法实质是对同一种物理现象的不同表征形式，三者可以通过一定的方式进行转化[14]。现阶段第一类方法已经被证明具有潜在应用价值，由于其与实验观测值的相似性获得了初步验证，是较为常用的方法。目前数字岩心技术已广泛应用于包括致密砂岩、页岩、砂砾岩等岩心的孔隙结构和渗流特征的研究中[15-17]，但采用该方法对油砂孔隙空间的研究还未见相关报道。

本文以风城油田侏罗系齐古组油砂为研究对象，通过CT 物理实验法重构了不同尺寸油砂的数字岩心，提出油砂图像中颗粒、沥青质和孔隙3 种介质图像分割方法，建立包含与不包含沥青质的2 种油砂骨架结构模型、孔隙空间模型和三维孔隙网络模型，进行油砂孔隙尺度流动模拟，分析不同数字岩心的流场和压力场分布特征，揭示风城油田天然油砂样品中沥青质相变对渗透率的影响机制，为明确风城油田油砂孔隙结构和渗流特征提供理论依据。

1 样品处理

实验样品取自风城油田侏罗系齐古组井下油砂岩心。由于油砂结构疏松、对温度敏感、易扰动，在冬季温度较低时取心，运输过程采用干冰降温，到达实验室后在-20 ℃的冷柜中储存，取心、运输和样品保存均在低温下进行。微米CT 实验的样品采用直径为25.0 mm、高度为50.0 mm 的标准岩心柱，通过液氮切割的方式制备样品，制样过程尽可能避免摩擦和震动，以降低对油砂岩心结构的影响[18]。

在扫描过程中采用了Xradia 公司生产的Microxct-200微米CT，分辨率为0.5～35.0 μm，通常粗粒砂岩要求图像分辨率为15.0～20.0 μm，疏松砂岩要求图像分辨率为5.0～15.0 μm[19]，因而本文实验采用的设备能够准确识别样品中的孔隙，并计算其大小，分析其分布情况。为了更加全面地表征油砂样品的细观结构特征，对样品进行了不同精度的多次扫描。先扫描直径为25.0 mm、高度为50.0 mm 的标准岩心柱，获得3 403张分辨率为12.0 μm的灰度图像；再对样品中心直径为10.0 mm、高度为6.5 mm 的圆柱形区域精细扫描，获得1 306 张分辨率为5.0 μm 的灰度图像；最后针对2组图像分别进行图像处理与数字岩心重构。

2 油砂孔隙结构数字岩心表征

数字岩心表征流程主要包括以下3 部分：使用高分辨率CT 获取岩心灰度图像，对图像进行处理与分割，数字岩心三维重构（图1）。但油砂的特殊性在于其包括颗粒、沥青质和孔隙3 种介质，这使得传统采用单一阈值划分孔隙和骨架的方法不再适用。因此，如何准确区分出颗粒、沥青质和孔隙3 种介质，建立适用于油砂3 种介质图像分割方法，是油砂数字岩心构建的关键。

图1 基于CT的油砂数字岩心重构流程Fig.1.Reconstructing process for digital oil sand cores based on CT scan

2.1 介质图像分割

以致密砂岩为代表的多孔介质，通常只包括孔隙和颗粒2部分[20]，其孔隙和颗粒灰度值相差较大，只要选取合适的阈值，就能将二者准确区分。油砂包括孔隙、颗粒和沥青质3 种介质，颗粒分选性较差，沥青质分布无规律，不同介质之间接触关系复杂，且沥青质和颗粒的灰度差异较小，区分度过低，给两者的划分带来了挑战。因此，采用现有阈值分割方法难以实现对油砂灰度图像中3种介质的划分。

为了解决上述问题，考虑油砂灰度图像特点，提出了适用于油砂的3 种介质图像分割方法。流程如图2 所示，首先区分出岩石骨架和孔隙（一次划分），并将计算获得的孔隙度与实测值进行对比，作为阈值依据（一次阈值调整）；再从岩石骨架中区分出颗粒和沥青质（二次划分），并将计算获得的沥青质含量与实测沥青质含量进行对比（二次阈值调整）。阈值可由非局部均值滤波过程来确定，进而获得具有不同峰值的曲线，将通过滤波获得的孔隙度与岩心实际测试孔隙度进行对比，若与实测值一致，则将该阈值作为孔隙介质灰度阈值的划分标准，由此可分割出孔隙与骨架。同理将实测沥青质含量作为标准值来确定颗粒和沥青质的划分阈值，可将骨架进一步分割，最终获得孔隙、颗粒和沥青质3种介质的分割图像。

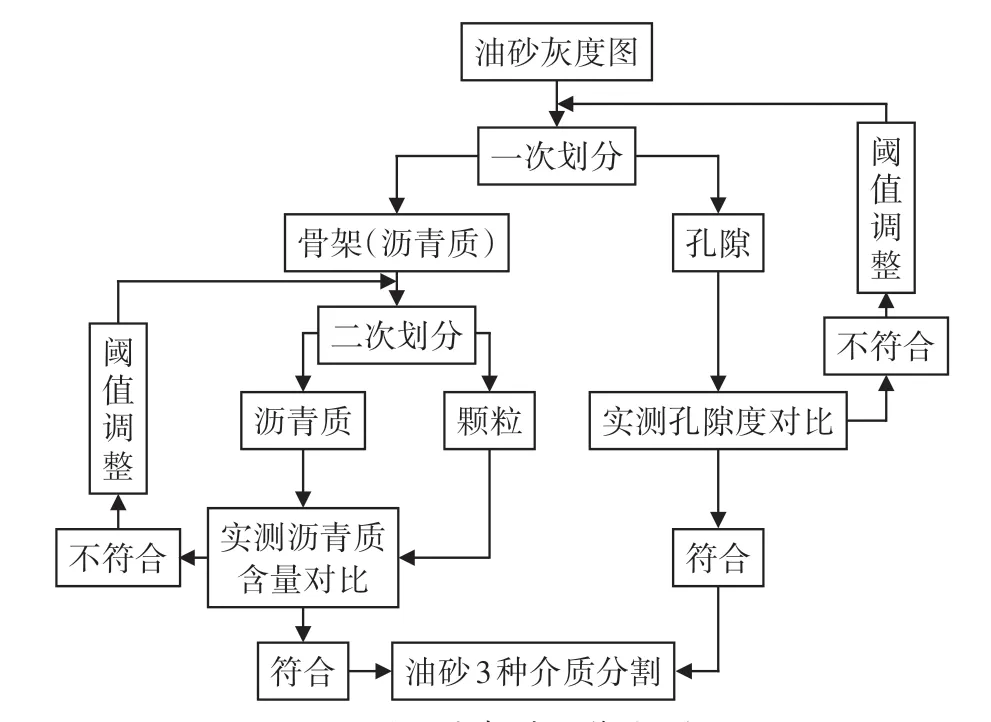
图2 油砂3种介质图像分割方法Fig.2.Three-medium image segmenting method for oil sands

在阈值划分的基础上，结合CT 图像观察油砂细观结构，可见油砂颗粒与沥青质接触关系主要包括3 种类型。第一种是接触，结构单元中只有颗粒相互接触，不同粒径的颗粒聚集在一起，颗粒间以点接触为主，局部颗粒呈线接触。第二种是胶结，结构单元中同时具有颗粒和沥青质，但沥青质较少，颗粒之间由少量沥青质充填胶结，沥青质呈薄膜状黏附在颗粒周围，此时颗粒之间呈点接触或线接触。第三种是悬浮，颗粒由沥青质完全包裹，俗称“油包砂”，颗粒间互不接触，呈悬浮状态，颗粒间完全靠沥青质支撑。

2.2 三维孔隙结构重构

基于现有的CT 图像，可以运用直接立体成像的方法实现油砂的三维重构。该方法所获取的是无损图像，只要准确划分出不同介质，便能较为准确地表征孔隙空间。图3 展示了重构后的油砂三维孔隙空间和骨架结构，这些实体结构为后期开展孔隙级流动模拟提供了几何模型，通过建立孔隙网络模型，并通过求解Navier-Stokes 方程的方式来研究流体在油砂中的流动。

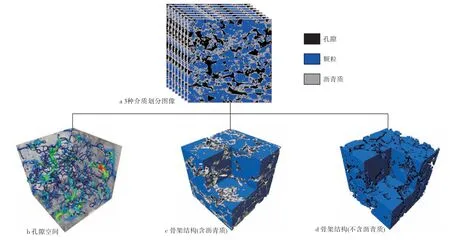
图3 油砂三维孔隙空间和骨架结构重构Fig.3.Reconstruction of three-dimensional pores and framework of oil sands

3 细观尺度油砂渗流模拟

3.1 孔隙网络建模

由于孔隙空间较为复杂，为开展孔隙尺度流动模拟，需要建立孔隙网络模型，进而获得孔隙和喉道的大小、数量等参数。中轴线算法的拓扑结构准确，计算量小，适合进行复杂多重介质样品的研究。本文以中轴线算法作为孔隙网络提取方法，主要步骤包括孔隙空间骨架提取、孔隙和喉道的识别。为了获得能代表孔隙空间特征的简化的球棍结构，采用距离排序同伦细化算法来提取孔隙空间的中轴线骨架，通过分析骨架结构来分割孔隙空间，进而识别孔隙和喉道。

3.2 细观渗流模拟

3.2.1 控制方程及其求解

采用流体力学方法求解孔隙中流体流动的本质为求解Navier-Stokes 方程，即将孔隙中流体的流动看作自由流，可以通过如下控制方程描述[21]。

动量守恒方程：

连续性方程（质量守恒方程）：

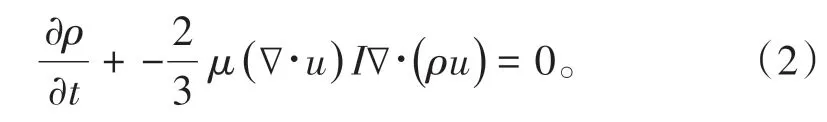
多孔介质中的流体流动非常缓慢，雷诺数非常小，此时的流动可视为蠕动流，即求解Navier-Stokes方程，整合后的控制方程为[22]

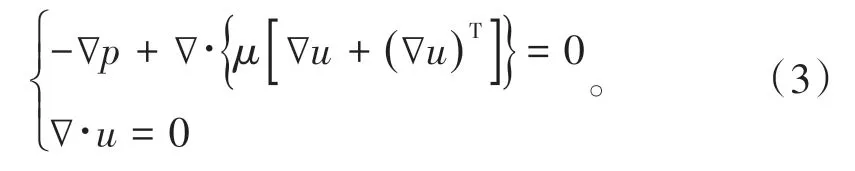
设定初始值和边界条件后便可预测流体流动速度和压力分布，通过在入口或出口边界处对流动速度进行积分，便可获得流过孔隙空间的流体流量，结合Darcy公式，便可获得宏观渗流参数，Darcy公式如下：

在用数值方法求解上式时，由于需要对相交网格进行离散以便更好地处理无滑移边界条件，因此采用有限体积法对控制方程进行求解。与传统划分网格的方式不同，本文采用三维数字岩心的代表性体积单元作为网格，压力未知数位于单元中心，速度未知数位于单元表面，并按照笛卡尔坐标系进行分解。

3.2.2 代表性体积单元分析

虽然在裁剪原始油砂数字图像时已经尽可能保留岩心结构信息，但基于观察结构特征定义代表单元的方法是定性的，要保证所建立的模型能够表征整个样品特征，需要进行代表性体积单元分析。本文采用的方法是以孔隙度作为约束，即通过对比分析随着所选立方体边长的增大，三维数字岩心中孔隙度的变化来实现。

用于CT的样品是直径为10.0 mm，高度为6.5 mm的圆柱体油砂，通过数字岩心重构技术和提取技术，以该样品圆柱中心点为中心，依次构建边长为0.5 mm，1.0 mm，1.5 mm，……，5.0 mm的立方体（图4），对比不同尺寸下的孔隙度和渗透率。

图4 代表性体积单元选取示意Fig.4.Schematic diagram of selection of a representative volume unit

应用前文的方法，对不同尺寸样品进行三维重构及孔隙网络建模。由于油砂中的沥青质温度敏感性强，具有两相性，需要分别分析2 种状态下的孔隙网络模型（图5）。在常温（25 ℃）下沥青质不能流动，被看作油砂骨架的一部分，此时模拟的是流体的有效渗流；当温度大于150 ℃时，沥青质成为可以流动的液态，此时油砂骨架部分只有骨架颗粒，模型计算的是油砂的绝对渗透率。这2 种孔隙网络模型，分别对应超稠油储集层快速启动阶段和SAGD 生产阶段的储集层油砂渗流状态。

图5 研究区不同尺寸代表性体积单元的孔隙网络模型Fig.5.Pore network models of representative volume units with different sizes

对于孔隙而言，圆球大小表征体积大小，颜色表征半径（红色为大孔隙，蓝色为小孔隙）；对于喉道而言，颜色表征半径，管径大小代表喉道粗细。有效渗流条件下，样品A1—A3 的孔隙结构差异明显；样品A5 未得到连通的孔隙，无法形成孔隙空间网络结构；样品A4、A6—A10 的孔隙结构较为相似，可以表征原有样品的孔隙结构（图6a）。绝对渗流条件下，样品A1—A4 的孔隙结构有明显差异，样品A5—A10 的孔隙结构较为相似，样品A5—A10基本可以表征原有样品的孔隙结构（图6b）。

图6 研究区不同尺寸代表性体积单元的孔隙度和渗透率Fig.6.Porosities and permeabilities of representative volume units with different sizes

为对油砂样品的渗流特征开展定量分析，分别计算不同渗流条件下样品的孔隙度和渗透率，并进行对比。样品A1—A3 的渗透率与样品A4—A10 的渗透率差距较大，因此不能用样品A1—A3 代表原有样品的孔隙度。样品A4—A10渗透率差距不大，与迂曲度和孔隙网络参数有关，从样品A4 到A10，孔隙度按照一定规律减小，有效孔隙度减小的速度更快（图6a）。样品尺寸随着样品编号增大逐渐增大，绝对渗流条件下，有效孔隙度与孔隙度基本一致，说明样品的孔隙连通性很好，孔隙度随着样品尺寸的增大而减小，渗透率随着样品尺寸的增大而减小，与孔隙度呈正相关，样品A4、A5 孔隙度和渗透率的变化较大，样品A6 是可以替代原有样品的最小尺寸样品（图6b）。综上所述，为准确表征风城油田侏罗系齐古组油砂特征，可以选取的代表性体积单元最小应为3.0 mm×3.0 mm×3.0 mm 的样品。

根据代表性体积单元选取原则，为了更加细致地研究油砂孔渗参数与渗流特征，对标准岩心柱扫描图像进行截取，获得直径为1.5 cm，高度为3.0 cm 的数字岩心，在该岩心中心截取6.0 mm×3.0 mm×9.0 mm的区域作为研究对象W，在W 的4个角和中心位置分别截取3.0 mm×3.0 mm×3.0 mm 的立方体样品，并依次编号为C1、C2、C3、C4 和C5（图7）。分别计算5 个子样品的孔隙度和x、y和z方向的绝对渗透率。

图7 油砂子样品选取示意Fig.7.Schematic diagram of selection of oil sand subsamples

（1）孔渗相对误差分析 经测定，样品W 的孔隙度为9.52%，子样品C1、C2、C3、C4 和C5 的孔隙度分别为11.53%、12.34%、14.49%、6.26%和8.53%，子样品的孔隙度与样品W 整体孔隙度的相对误差可以用以下公式计算：

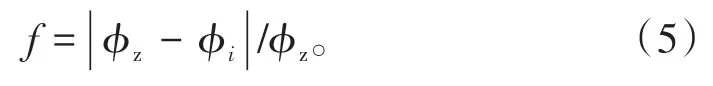
计算结果为，子样品的孔隙度与样品W 整体孔隙度的相对误差分别为21.11%、29.62%、52.21%、34.24%和10.40%。

计算得到子样品3个方向的渗透率，分别用Kx、Ky和Kz表示，计算子样品各方向渗透率与样品W整体渗透率的相对误差，公式如下：

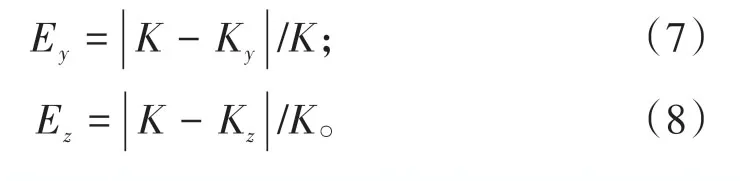
经计算可知，子样品孔隙度与样品W 整体孔隙度相对误差为10.40%～52.21%。而子样品各方向渗透率与样品W 整体渗透率的相对误差为0.44%～119.11%（表1），说明了油砂样品非均质性较强。

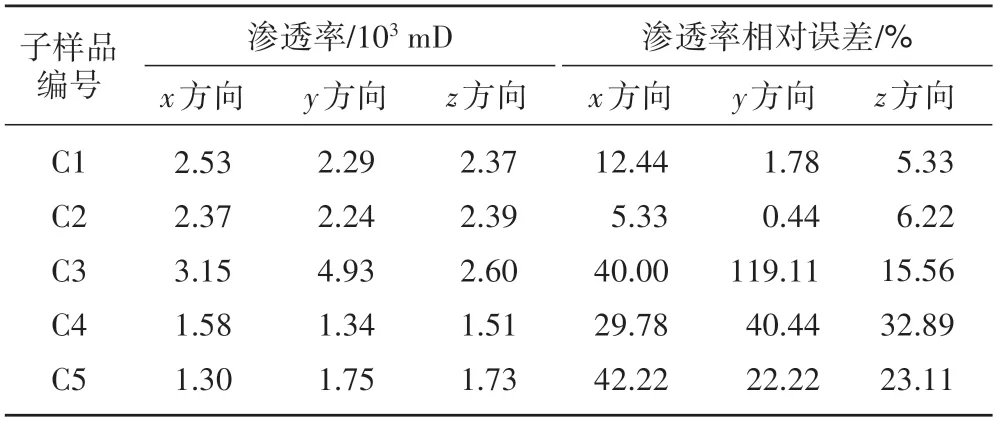
表1 研究区油砂子样品渗透率计算结果Table 1.Calculated permeability of subsamples of oil sands

（2）渗透率与孔隙度的关系 对比油砂5 个子样品3 个方向的渗透率与孔隙度可知，渗透率与孔隙度基本呈正相关，即孔隙度越大，渗透率越大。但在个别异常点二者也存在负相关的现象，原因在于该点上孔隙连通性差，导致渗透率随着孔隙度的增加而降低（图8）。

图8 研究区油砂子样品不同方向渗透率与孔隙度的关系Fig.8.Relationships between permeability and porosity in different directions

（3）流场和压力场特点 图9 为子样品C1、C3 和C5 的流场和压力场分布，不同样品的流场和压力场分布差异较大。x、y和z方向上的流场流动速度为C3＞C1＞C5，这与渗透率的大小一致，而压力场的变化也符合渗透率的变化规律，说明流场和压力场的分布可以更为形象直观地体现油砂的非均质性。

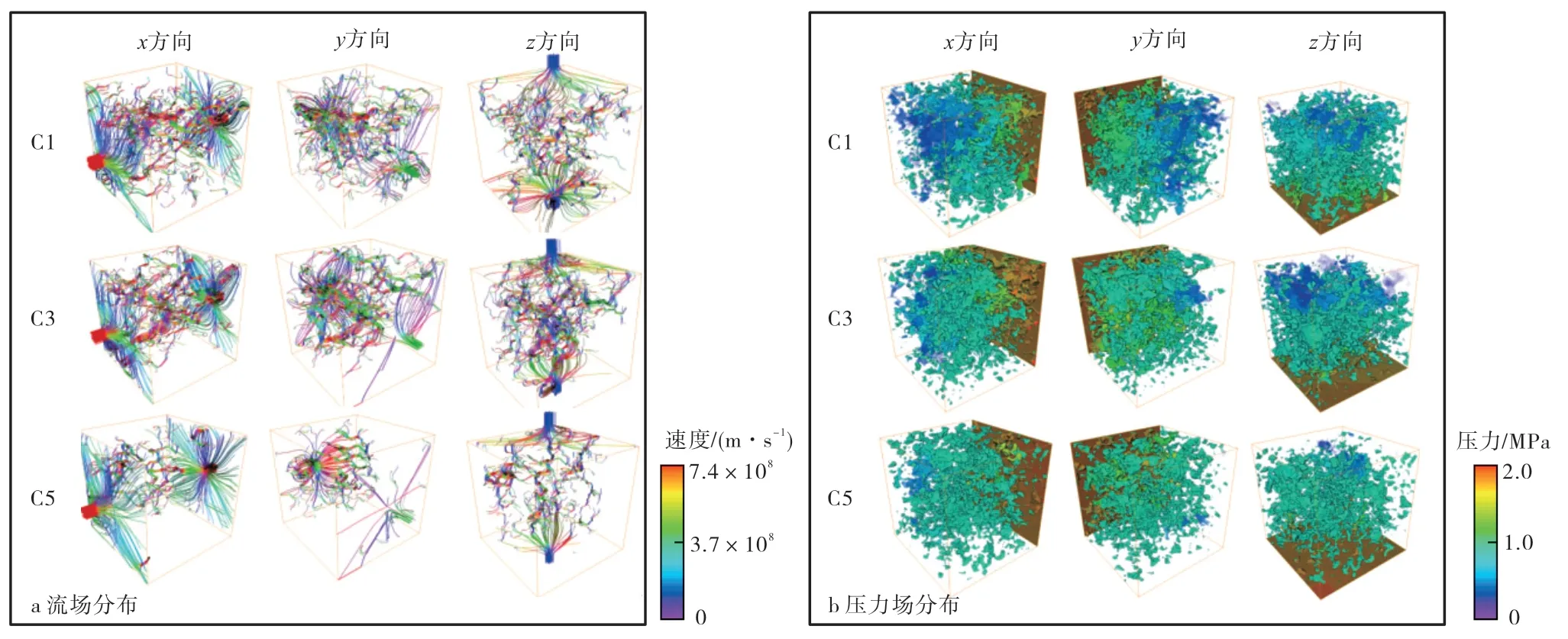
图9 研究区油砂子样品流场和压力场分布Fig.9.Distribution of flow field and pressure field of oil sand subsamples in the study area

（4）渗透率各向异性 通过计算得出5 个子样品不同方向渗透率的比值，z方向渗透率与x方向渗透率比值为0.83～1.33，z方向渗透率与y方向渗透率比值为0.53～1.13，x方向渗透率与y方向渗透率比值为为0.64～1.18。总体而言，油砂各个方向上的渗透率差异较大，这与油砂本身的非均质性和其成岩过程有关，说明油砂具有一定程度的各向异性。

4 结论

（1）油砂温度、应力敏感性强，通过直接自然断面图像研究油砂结构和进行渗透率参数测试均易破坏其本身结构，采用无损、非接触的CT 重构的数字岩心技术可有效获取未受扰动的油砂内部结构。

（2）风城油田齐古组油砂中颗粒和沥青质存在接触、胶结和悬浮3 种结构关系，油砂图像中颗粒、沥青质和孔隙3 种介质的分割效果决定数字岩心三维重构模型的准确程度。

（3）为了选取能代表风城油田齐古组油砂复杂结构的数字岩心，代表性体积单元应至少是边长为3.0 mm的立方体。

（4）风城油田齐古组油砂具有较强的非均质性和各向异性，沥青质的相态（成为骨架一部分或者成为孔隙流体）显著影响油砂的孔隙度、孔隙迂曲度和渗透率，不包含沥青质的骨架模型渗透率比包含沥青质的骨架模型渗透率高约2个数量级。

符号注释

Ex、Ey、Ez——分别为x方向、y方向和z方向渗透率相对误差；

f——相对误差函数；

F——流体受到的外力，Pa；

I——单位张量；

K——绝对渗透率，m2；

Kx、Ky、Kz——分别为x方向、y方向和z方向渗透率，mD；

L——流动方向样品长度，m；

p——流体压力，Pa；

△p——流体压差，Pa；

▽p——流体压力梯度，Pa/m

Q——通过样品的流量，m3/s；

S——流体通过多孔介质的截面积，m2；

t——时间，s；

T——转置符号；

u——流体流动速度，m/s；

▽u——流体流动速度梯度，s-1；

μ——流体动力黏度，Pa·s；

▽——哈密顿算子；

ρ——流体密度，kg/m3；

φi——子样品i的孔隙度，%；

φz——样品整体孔隙度，%。