层状海洋电性天线辐射电磁场高效模拟计算

时宗洋，赵一宇，渠晓东，马力超

（1.北京机械设备研究所，北京 100854；2.中国科学院空天信息创新研究院，北京 100094）

0 引言

典型层状海洋模型下任意姿态电性天线电磁场的模拟计算方法主要应用海洋目标电磁探测应用领域，如海底石油、水合物等探测的海洋可控源电磁方法和海水中大型目标如沉船等探测等。

以海洋可控源电磁方法（MCSEM）为例，其通常采用几百米长的水平电性天线在海水中（距海底几十米的位置）辐射峰值电流几百安培至千安培、基频在n×10-1Hz至n×10 Hz范围内的矩形波电流，通过布置在海底或者拖曳在距水平电性天线固定偏移距的电场或磁场传感器观测电场/磁场响应信号[1-2]，然后通过采用相适应的数据处理手段对电磁信号进行处理，运用预先建立的层状海洋模型正反演算法获得对实测电磁信号的定量反演解释，从而得到海洋中目标电阻率信息，图1给出了海洋可控源电磁法工作示意图，图中传感器阵列rxi(i＝1…N)位于海底沿电性天线轴向布置。

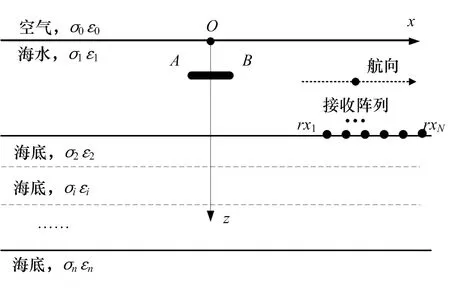
图1 海洋可控源电磁法(MCSEM)工作示意图

现有层状海洋模型电性天线辐射电磁场的模拟计算方法主要有2种，一种是将有限长电性天线看作电偶极子天线[3-4]，然后利用层状海洋模型下电偶极子天线辐射电磁场模拟解释海洋目标及海底电性参数；另一种方法是将有限长度电性天线进行均匀密集分割，将分割后每一段等效为电偶极子，再对每个等效电偶极子天线的电磁响应求和得到有限长电性天线的辐射电磁场。

以上计算方法存在以下缺点或不足之处，方法一将有限长电性天线看作电偶极子天线，这种方法认为：当海洋目标（海底或海水目标）和观测传感器距离电性天线很远（相比于电性天线长度）时电性天线可以等效为电偶极子天线。然而，实际MCSEM中的电性天线长几百米（一般100～300 m），距离海底几十米距离，航行作业时，电性天线从靠近海底的传感器阵列到远离传感器阵列的过程中，无法始终保证电性天线距离海底和传感器的距离远大于电性天线的长度（如5倍电性天线长度），从而导致该方法在计算小偏移距的电磁场时产生较大的计算误差。方法二均匀密集分割有限长度电性天线，然后把分割后的每段等效为电偶极子，并对每个等效电偶极子天线的电磁响应求和得到有限长电性天线的辐射电磁场。该方法在保证计算精度的同时会极大地降低计算效率，不利于工程应用中数据资料的快速解释[5]。

本文针对层状海洋模型电性天线辐射电磁场的模拟计算现有方法无法兼顾计算精度和计算效率的不足，提出了一种典型层状海洋模型中任意姿态电性天线辐射电磁场的非均匀稀疏分割计算方法，采用切比雪夫多项式的零点作为分点，对原有的均匀分割方案进行了以切比雪夫多项式零点为分点的非均匀稀疏分割方案的改进，实现了有限长电性天线的精确快速计算，兼顾了计算的精度和效率。

本文首先介绍典型层状海洋模型下电性天线辐射电磁场的工程应用及现阶段主要计算方法和存在的不足，引出本文建立的非均匀稀疏分割积分方法及其优势；然后构建了层状海洋模型电磁天线辐射电磁场模型，并对电磁场积分计算式进行了理论推导，并且建立基于高斯切比雪夫分点的非均匀稀疏分割积分方法，给出理论计算式和算法流程；接下来通过模拟仿真算例，对电偶极子等效计算方法、密集均匀分割积分方法和本文提出的非均匀稀疏分割积分这3种方法在电磁场计算精度和效率方面进行对比分析，论证了本文提出方法在兼顾计算精度和效率方面的优势，能够实现工程应用中数据解释的效率和准确性的提升；最后对全文进行总结，给出结论。

1 层状海洋电性天线辐射电磁场理论

1.1 典型层状海洋模型

以典型3层海洋模型为例，即空气层、海水层和海底层。其中，空气层设定为半无限大均匀空间，海底层可以为半无限大均匀空间或层状空间，海水层深度为d1，设定分解面互相平行，水平方向上无限延伸，空气、海水和海底（可以为多层海底）的介电参数分别为σi、εi（i＝0,1,2,…,n,n≥2），其中i＝0表示空气层，i＝1表示海水层。真空磁导率为μ0，相对磁导率μr设置为1。AB表示电性天线首尾，天线长度为L，天线电极矩为P＝IL，天线中点位于原点O正下方，目标所在深度为H，距离海底深度为h，各层厚度为d i。笛卡尔坐标系正z方向垂直水平面向下，o-xyz满足右手螺旋定则。假设任意姿态电性天线在XOY平面内的投影与x轴夹角为θ，天线与XOY平面的夹角为ϕ。

层状海洋模型电性天线模型如图2所示。层状海洋模型下电性天线辐射电磁场的推导基于以下假设[6-8]：

图2 层状海洋模型中的电性天线

1）满足准静态近似条件，频率小于100 k Hz；

2）准静态近似下忽略海水和海底环境的位移电流，波数为k2i＝-iωμ0σi，i＝1,2,…,n。空气中仅存在位移电流，约定电导率为σ0＝iωε0，波数为k20＝

3）空气、海水及同层海底媒介时各向同性的，参数与时间、温度和压强无关；

4）准静态近似下，认为媒介参数与频率无关，磁导率和介电常数采用真空中的参数。

对于没有自由电荷的空间，电性天线在空间中产生的电磁场满足如下麦克斯韦方程组。

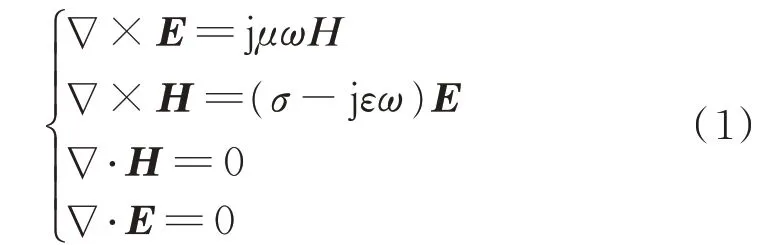
定义电矢量为A，满足Η＝∇×Α。得到电场与电矢位关系：

式中，U为标量位，满足

1.2 电偶极子天线辐射电磁场

1.2.1 水平电偶极子天线频域电磁场

层状海洋模型下水平电偶极子天线如图3所示，其对应的电磁场具有对称性，此时的电矢量位A仅包含了2个分量，即沿偶极矩方向的分量A x和沿垂直海水-空气分解面的分量A z。电矢量位A在笛卡尔坐标系下可表示为：

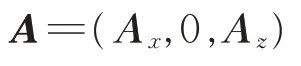
矢量位、电场及磁场满足的边界条件为[8-10]：

1）整个空间中，除发射源位置外，矢量位A处处为有限值，且在无穷远处，矢量位为零，即Α(r→∞)→0；

2）各层分解面上，电场和磁场的切向分量连续。

根据边界条件约束，电场E、磁场H与矢量为A和标量位U之间的关系，采用分离变量法可得到各层中矢量位各分量的解。

空气中电场和磁场各分量频域计算式见式(3)和式(4)。

式中，ϕ为观测点与电偶极源位置连线在XOY平面投影与x轴的夹角，sinϕ＝y/r，cosϕ＝x/r。

海水中电场和磁场各分量频域计算式见式(5)和式(6)。

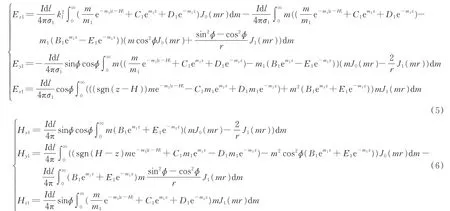
式中，Idl表示电偶极源的电矩，m为积分变量，r＝(x2＋y2)1/2为收发距，mi＝(m2-k2i)1/2，i＝0,1,2,…,N。积分核中的Ji(mr),i＝0,1代表第i阶贝塞尔函数。参数Ci、B i、D i和E i为待定系数，通过理论推导计算结果如下：

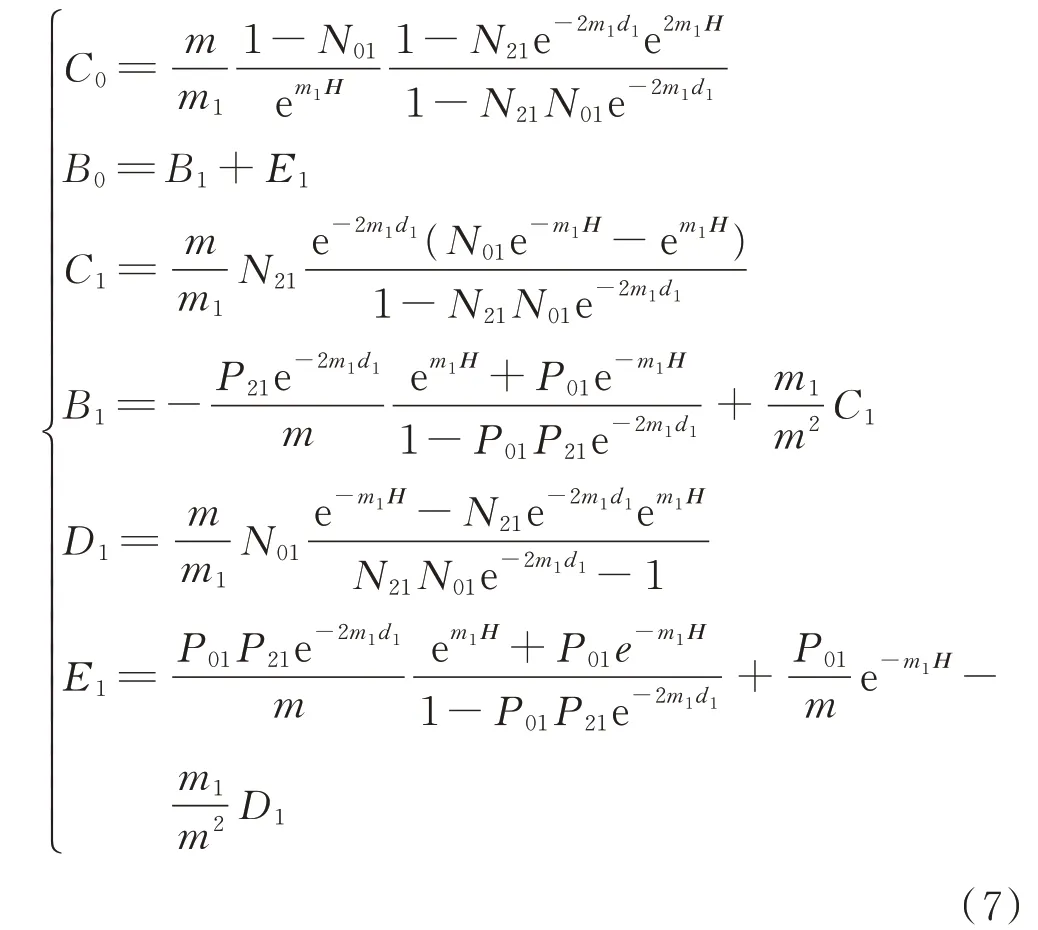
式中，N01、N21、P01和P21计算式如下：

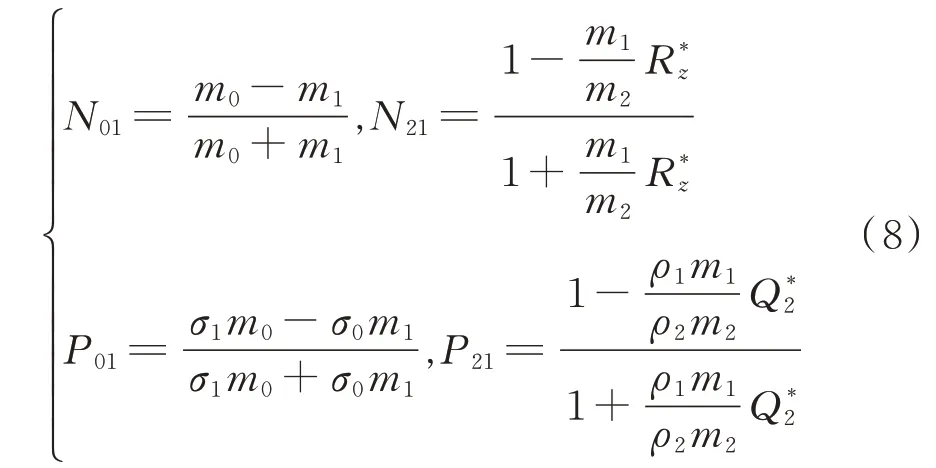
式中，R*2和Q*2的递推计算式为：

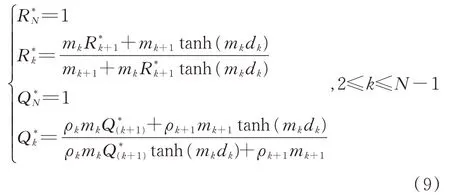
1.2.2 垂直电偶极子天线频域电磁场

层状海洋模型下垂直电偶极子天线示意图如图4所示，其电矢位A仅包含沿偶极矩方向的分量A z[11]。此时的电矢量位A在笛卡尔坐标系下表示为：

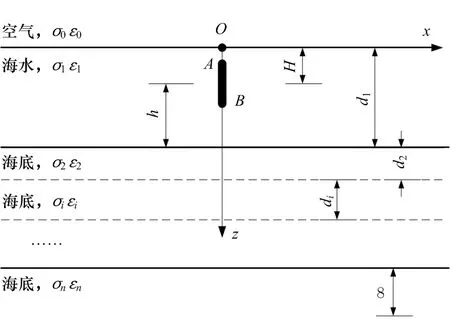
图4 层状海洋模型下垂直电偶极子天线

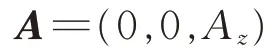
根据边界条件约束，及电场E、磁场H与矢量为A和标量位U之间的关系，采用分离变量法可得到各层中矢量位各分量的解。

空气中电场和磁场各分量频域计算式见式(10)和式(11)。

海水中电场和磁场各分量频域计算式见式(12)和式(13)。

式中，参数Ci和D i为待定系数，通过理论推导计算结果如下：

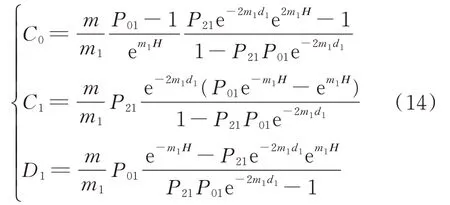
式中，P01和P21计算式如下：

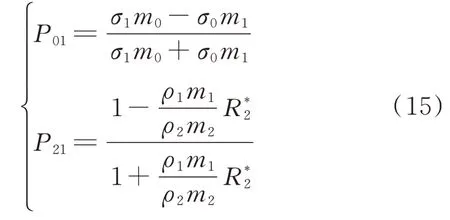
式中，R*2的递推计算式如下：

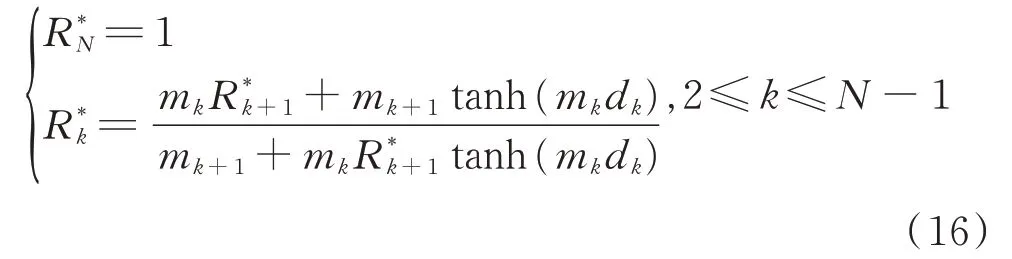
1.2.3 任意姿态电偶极子天线频域电磁场

海水中任意姿态电偶极子天线辐射电磁场计算时，将偶极矩分别向x,y和z轴投影，然后分别计算三分量投影电偶极子Px、Py和Pz的电磁场，最后将各方向电偶极子天线的电磁场求和即可[12-13]。层状海洋模型下任意姿态电偶极子天线如图5所示。

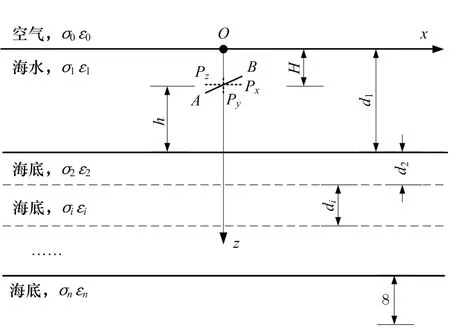
图5 层状海洋模型下任意姿态电偶极子天线

式中，沿y方向的电矩为Py的电偶极子天线产生的电磁场，可以通过计算沿x方向的电矩为Py的电偶极子天线的电磁场然后通过坐标变换得到。

1.2.4 电偶极子天线电磁场计算方法

层状海洋模型下电偶极子天线辐射电磁场的计算方法流程如图6所示。该算法包含了辐射电磁场的频域和时域模拟计算方法，总体思路是首先根据电偶极子天线辐射电磁场的频域计算式通过快速Hankel变换数值滤波方法实现频域模拟计算，获得频域电磁结果；然后通过GS变换数值滤波方法实现快速的频-时变换，得到时域电磁计算结果[14-15]。

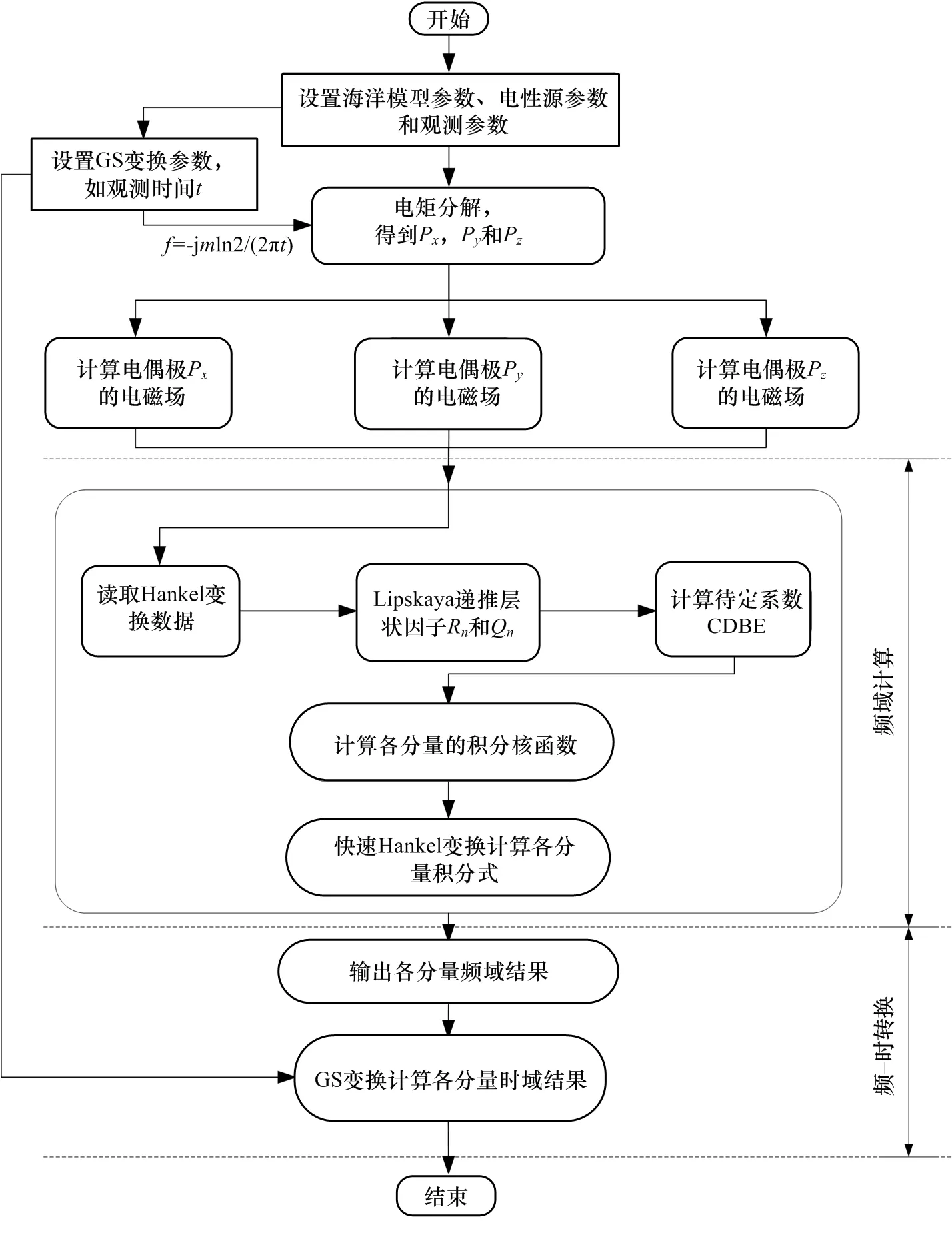
图6 层状海洋模型电偶极子天线辐射电磁场计算流程

1.3 有限长电性天线辐射电磁场

1.3.1 任意姿态电性天线辐射电磁场的积分计算式

理论上，典型海洋模型下任意姿态有限长电性天线辐射电磁场的计算需要通过对天线长度进行积分获得。

假设电性天线l位置的电偶极子在观测位置r处产生的响应（电场或磁场）表示为f(p,θ,ϕ,l,r)，其 中f(·)可 以表 示 辐 射 电 磁 场E x、E y、E z、Bx、B y、B z的计算式，θ和ϕ为已知参数，p＝Idl，p表示天线l位置处的电偶极子极矩，I为天线中电流强度，dl表示l位置的偶极子单位长度，l和r分别为电偶极子天线和观测点的相对于坐标原点的位置矢量。因此，有限长电性天线的电磁场计算式为：

1.3.2 现有电性天线辐射电磁场的积分计算方法

现有的电性天线辐射电磁场的积分计算方法主要采用电偶极子天线等效方法和均匀密集分割积分方法。对于电偶极子天线等效方法，是将有限长电性天线看作电偶极子天线，此时积分式(18)变为：

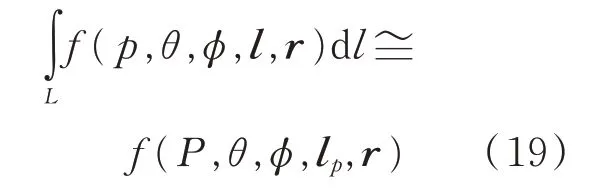
式中，l p表示有限长电性天线中心位置的位置矢量。

对于均匀密集分割积分方法是将积分式(18)均匀离散化为众多的电偶极子天线响应之和的形式。

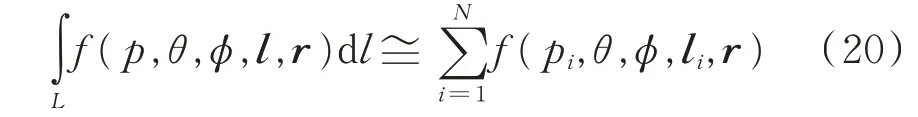
式中，N为均匀分割的分点数，一般为保证计算精度，对于长度100 m以上的天线，N取值不小100。

2 层状海洋电性天线辐射电磁场的非均匀稀疏分割计算方法

为解决现有方案在计算效率和精度无法兼顾的不足，本节将基于切比雪夫多项式零点建立适于加速计算电性天线辐射电磁场的非均匀稀疏分点的高斯-切比雪夫积分方法，以保证了计算精度的同时极大的减小了积分节点数，提升了计算效率。

2.1 基于高斯—切比雪夫积分的非均匀稀疏分割计算方法

在高斯勒让德数值积分方法在地面有限长电性天线辐射电磁场加速计算方面的应用发展基础上[9,16]，本论文提出基于高斯—切比雪夫积分的非均匀稀疏分割方法，利用具备带权正交性的切比雪夫多项式的零点作为高斯积分点，采用带权值的拉格朗日插值多项式计算积分系数，并通过对积分核函数的构造实现快速精确的计算。下面给出基于高斯-切比雪夫积分的非均匀稀疏分割计算方法的流程。

1）求n＋1次切比雪夫多项式的n＋1个零点，用于后续产生积分节点。

由于切比雪夫多项式在区间[-1,1]内带权值ρ(x)＝(1-x2)-1/2,x∈[-1,1]正交性，n＋1次切比雪夫多项式的n＋1个零点也是高斯点，对应的高斯-切比雪夫积分的代数精度是2n＋1次的。切比雪夫多项式满足下面的递推关系式：

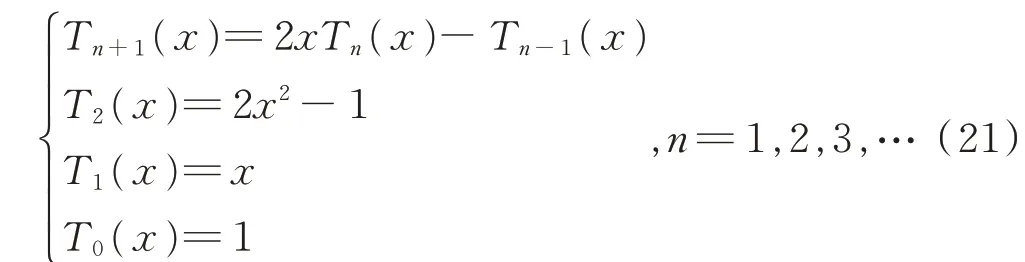
其对应的n＋1个零点为：

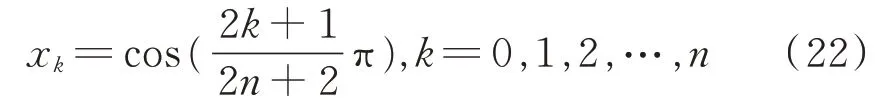
2）计算各节点对应的带权值ρ(x)＝(1-x2)-1/2,x∈[-1,1]的拉格朗日插值基函数l k(x)，用于计算各积分节点对应的积分系数。x k对应的拉格朗日插值基函数l k(x)为：

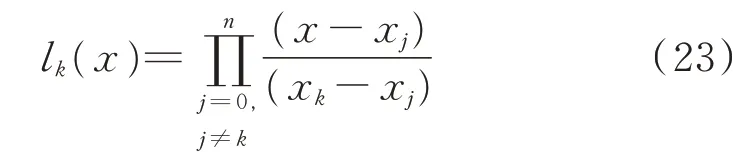
3）求各积分节点对应的积分系数A k，计算式为：

4）积分区间变换，调整积分区间与有限长电性天线长度范围匹配。

积分节点x k及其对应积分系数A k与积分区间无关，仅与分点数（积分阶数）有关。因此，算法实现时可以将常用阶数的积分节点和积分系数存储以备随时调用，以此获得额外的加速计算效率。积分区间变换式如下：

式中，a和b分别为电性天线长度范围对应的坐标。

当计算天线的X轴分量时，b＝L x/2，a＝-L x/2，计算得到的为天线X轴分量各分点坐标l xk；

当计算天线的Y轴分量时，b＝L y/2，a＝-L y/2，计算得到的为天线Y轴分量各分点坐标l yk；

当计算天线的Z轴分量时，b＝L z/2，a＝-L z/2，计算得到的为天线的Z轴分量各分点坐标l zk。求解过程中的x k保持不变。L x、L y和L z通过投影变化得到：

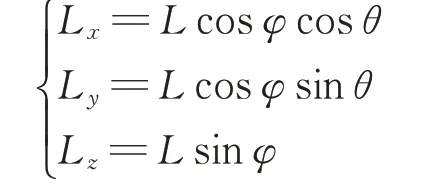
5）代入式（25）中计算任意姿态有限长电性天线的辐射电磁场。

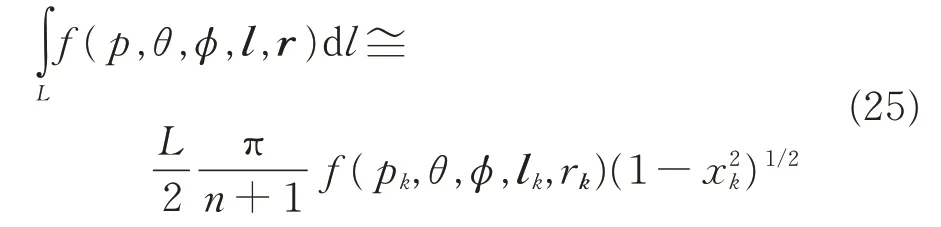
本文建立的基于高斯-切比雪夫积分方法进行典型层状海洋模型任意姿态有限长电性天线电磁场的快速计算方法，是以n＋1次切比雪夫多项式的零点作为积分节点构建代数精度为2n＋1次的积分求解方法，实现了非均匀稀疏分割积分方法，以保证计算效率和精度。

2.2 模拟计算结果与性能分析

为验证本文提出方法的效果，表1给出下列模拟仿真计算案例，以对比本文提出方法相比现有计算方法的性能提升。

表1 模拟仿真案例参数列表

图7 —14给出了海底沿x轴和y轴方向0～1 km范围内磁感应强度总场、各分量及电场总场和各分量的幅度和相位分布曲线。从幅度分布曲线的计算结果可知，电偶极子天线近似计算结果误差最大，甚至短偏移距时的分布曲线形态已无法反应真实分布曲线形态，如图8和图12给出的电场总场及各分量幅度分布曲线；从相位分布曲线计算结果可知，电偶极子天线近似计算结果的相位分布在短偏移距时存在较大误差，如图10和图14所示。对比均匀密集分割频域计算结果与本论文提出方法的频域计算结果可知，本文方法的计算结果与均匀密集分割计算结果精度相当，幅度和相位分布曲线具有很好的一致性。

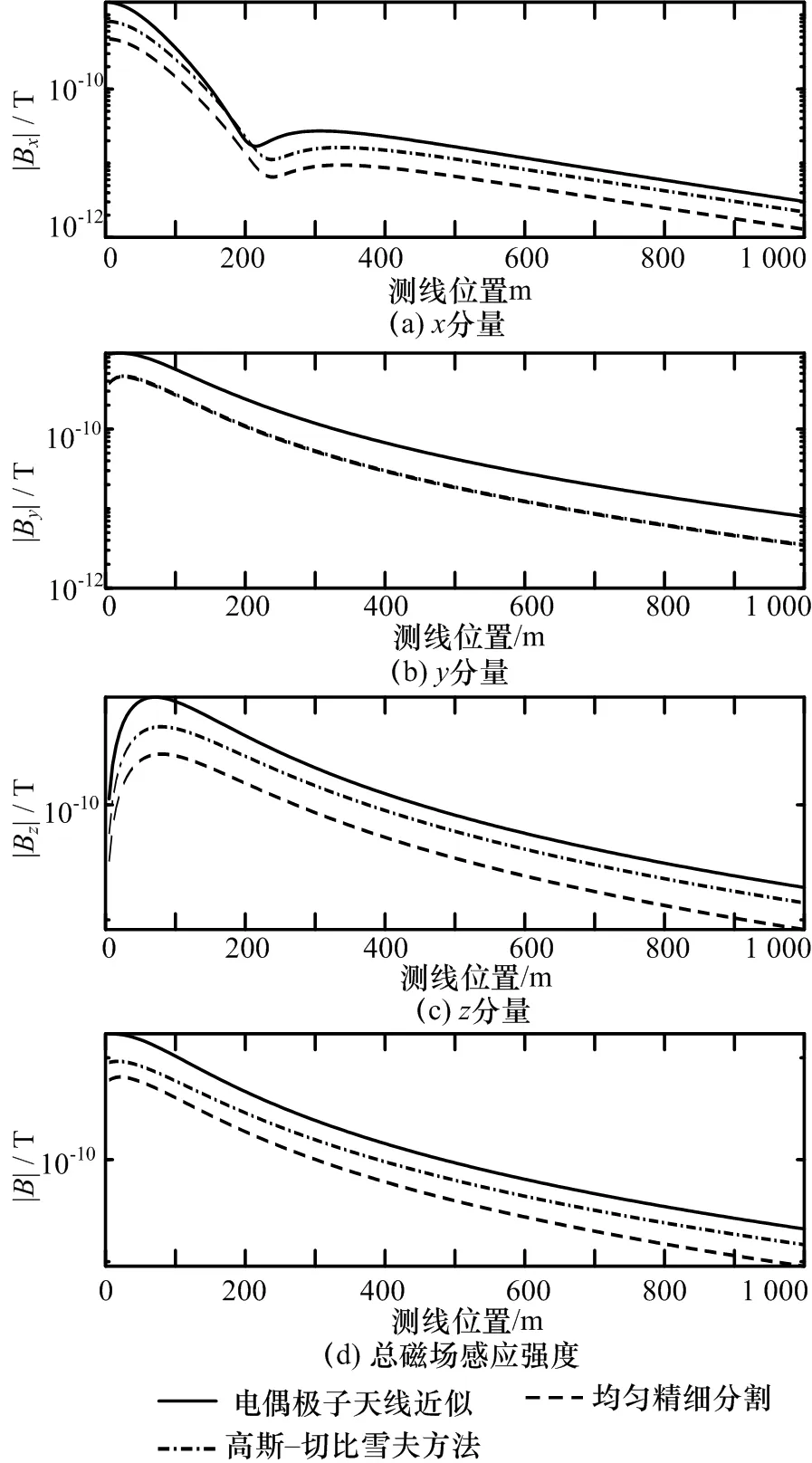
图7 海底x方向0～1 km范围内磁感应总场及各分量的幅度分布曲线

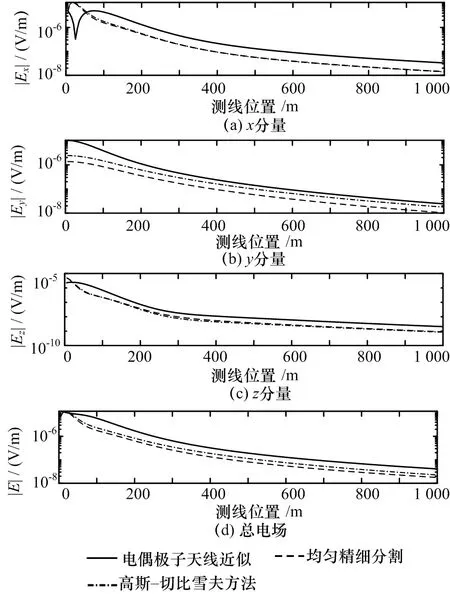
图8 海底x方向0～1 km范围内电场总场及各分量的幅度分布曲线

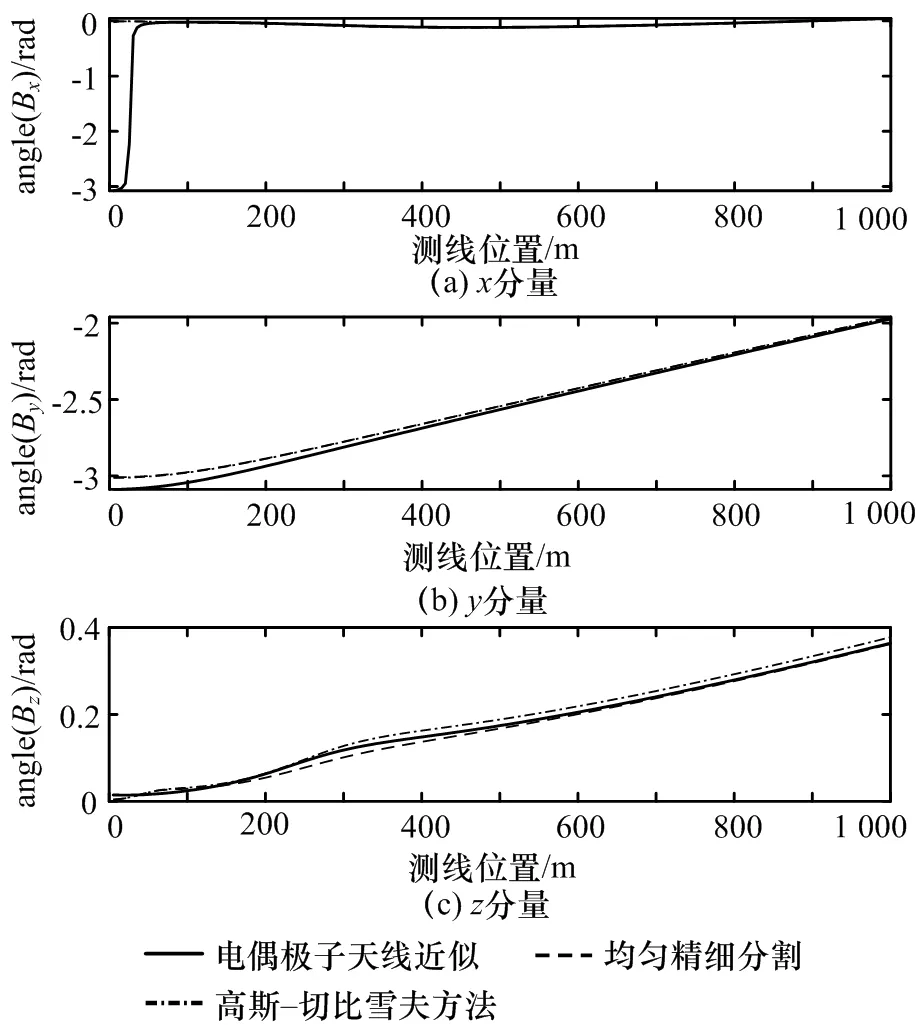
图10 海底x方向0～1 km范围内电场各分量的相位分布曲线

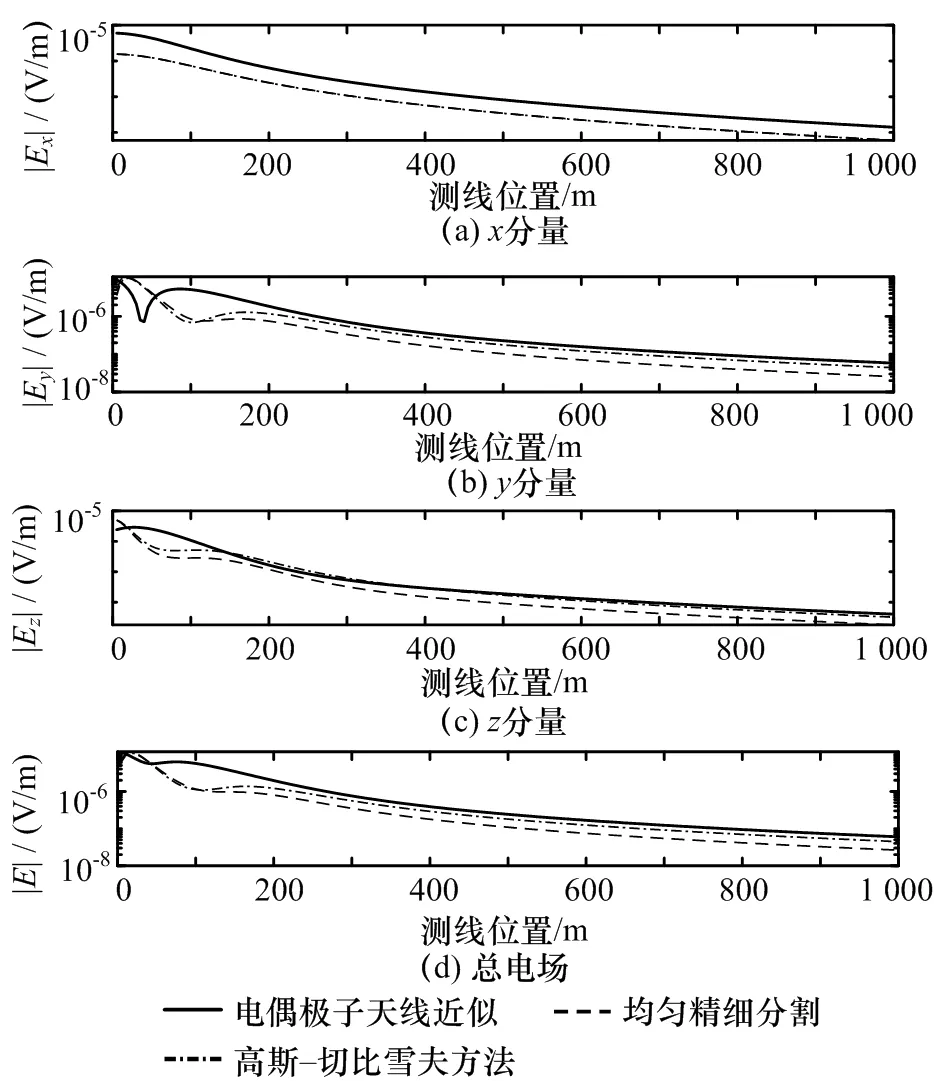
图12 海底y方向0～1 km范围内电场总场及各分量的幅度分布曲线

图14 海底y方向0～1 km范围内电场各分量的相位分布曲线

图15和图16出了海底（0,500 m）位置的磁感应总场、各磁场分量、电场总场和各电场分量的负阶跃响应曲线。其中，实线为电偶极子天线近似结果，划线为均匀精细分割计算结果，点线为本文提出的基于高斯-切比雪夫积分方法的非均匀稀疏分割积分计算结果。

图9 海底x方向0～1 km范围内各磁感应强度分量的相位分布曲线

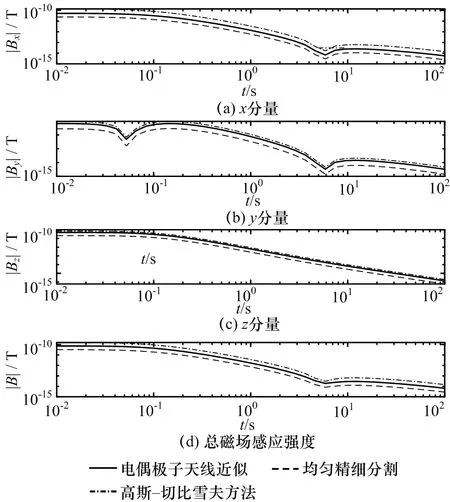
图15 海底(0,500 m)位置的磁感应总场及各分量的负阶跃响应

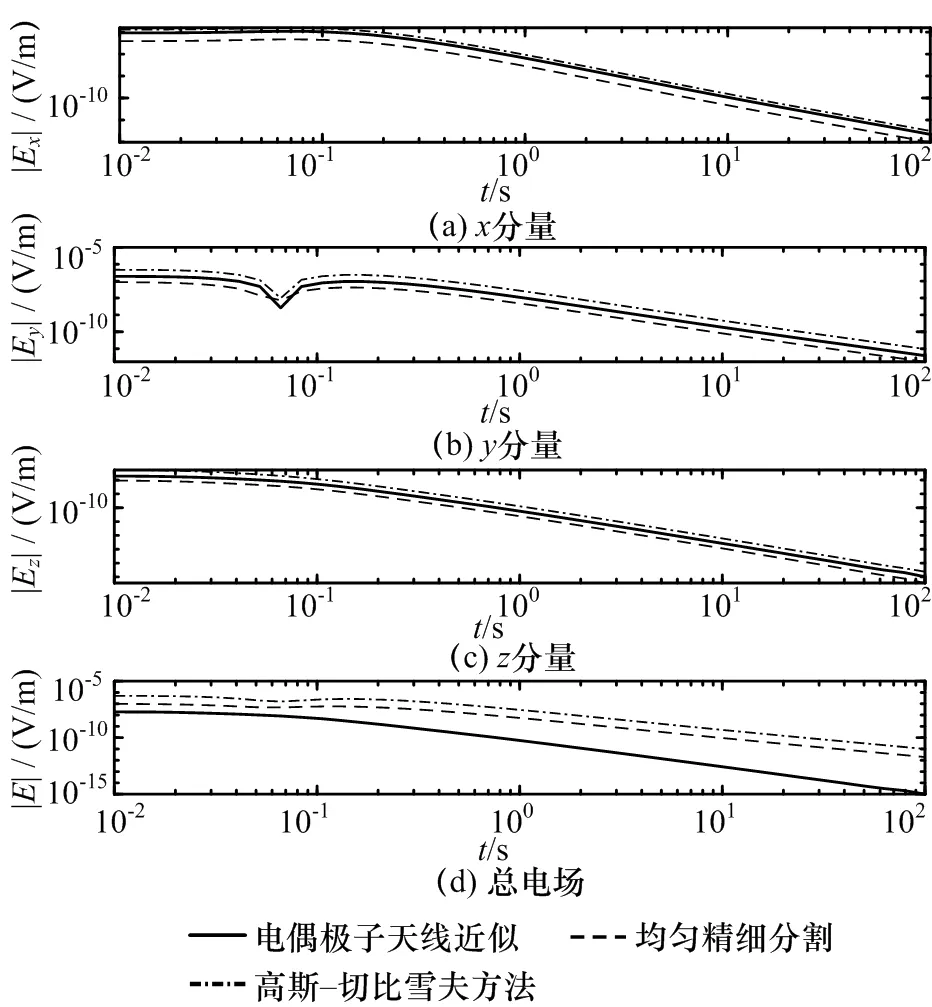
图16 海底(0,500 m)位置的电场总场及各分量的负阶跃响应

在计算机配置为Win7系统，六核Intel i5-8400，主频2.80 GHz，8 GB RAM条件下，仿真软件采用MatlabR2018a-64位版本，模拟计算单频点，200个观测点6个分量的仿真计算耗时间如表2所示。推荐使用的非均匀稀疏分割计算参数为积分节点数7～13，误差限1e-8～1e-12。

表2 计算耗时统计 s

图11 海底y方向0～1 km范围内磁感应总场及各分量的幅度分布曲线

对比本文方法与电偶极子天线近似计算方法、均匀密集分割计算方法的计算结果精度和计算效率可知，在保证计算精度的情况下，本文提出的方法对层状海洋有限长电性天线辐射电磁场的时域和频域计算效率的提升达10倍以上。

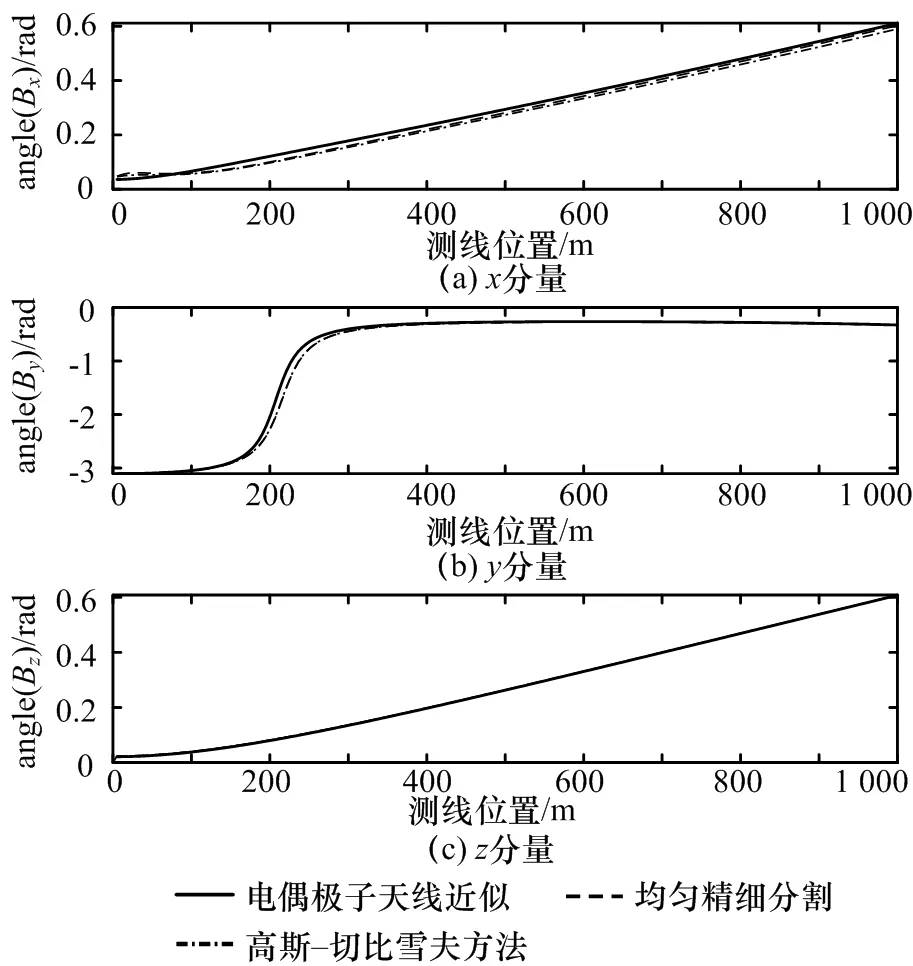
图13 海底y方向0～1 km范围内各磁感应强度分量的相位分布曲线

3 结束语

本文针对当前层状海洋下电性天线辐射电磁场时频域计算精度和效率无法兼顾的问题，基于高斯-切比雪夫积分方法，构建了适用于层状海洋模型电性天线辐射电磁场的非均匀稀疏分割快速计算方法，通过采用n＋1次切比雪夫多项式的零点作为分点，实现将原有的密集均匀分割点数极大地减小到以切比雪夫多项式的n＋1个零点为分点的非均匀稀疏分割计算方案，在保证计算精度的前提下，实现了有限长电性天线辐射电磁场的快速计算，兼顾了计算的精度和效率。这种非均匀稀疏分割积分方法能够实现工程应用中数据解释的效率和准确性的提升。■