黑猩猩优化算法-极限学习机模型在富水性分级判定中的应用

程国森 崔东文

摘 要：為提高煤层顶底板地层富水性分级判定精度，研究提出黑猩猩优化算法（ChOA）与极限学习机（ELM）相融合的判定方法。选取4个标准测试函数在不同维度条件下对ChOA的寻优能力进行仿真验证，仿真结果与粒子群优化（PSO）算法、人工蜂群（ABC）算法作对比;基于煤层顶底板地层富水性判定因子和判定分级构建ELM模型，利用ChOA优化ELM输入层权值和隐含层偏值，建立ChOA-ELM富水性分级判定模型，并构建ChOA-SVM、ChOA-BP作对比模型，通过龙固煤层顶底板地层富水性分级判定实例对ChOA-ELM、ChOA-SVM、ChOA-BP模型进行检验。结果表明：①ChOA在不同维度条件下寻优效果优于PSO、ABC算法，具有较好的寻优精度和全局搜索能力;②ChOA-ELM模型对实例训练样本和检验样本富水性分级判定准确率分别为97.5%、100%，高于ChOA-SVM、ChOA-BP模型，具有较好的判定精度和泛化能力;③ChOA能有效优化ELM输入层权值和隐含层偏值，将ChOA-ELM用于煤层顶底板地层富水性分级判定是可行的，模型及ELM权值、偏值优化方法可为相关判定研究提供参考。

关键词：富水性;分级判定;极限学习机;黑猩猩优化算法;仿真验证;参数优化

中图分类号：TV213.4;P641.5+4 文献标志码：A

doi：10.3969/j.issn.1000-1379.2021.07.012

引用格式：程国森，崔东文.黑猩猩优化算法-极限学习机模型在富水性分级判定中的应用[J].人民黄河，2021，43（7）：62-66，103.

Abstract： In order to improve the classification accuracy of the water-rich stratum in the roof and floor of the coal seam， this paper proposed a judgment method combining the chimpanzee optimization algorithm （ChOA） and the extreme learning machine （ELM）. It chose 4 standard test functions to simulate and verify the optimization ability of ChOA under different dimensional conditions. The simulation results were compared with the particle swarm optimization （PSO） algorithm and the artificial bee colony （ABC） algorithm. It based on the determination of the water richness of the roof and floor of the coal seam factor and decision grading to build an ELM model， used ChOA to optimize ELM input layer weights and hidden layer bias， established a ChOA-ELM water-rich grading decision model， and built ChOA-SVM and ChOA-BP as comparison models. The example of determining the water richness of the roof and floor strata was to test the ChOA-ELM， ChOA-SVM and ChOA-BP models. The results show that： a） ChOA has better optimization results than PSO and ABC algorithms under different dimensional conditions， and has better optimization accuracy and global search capabilities; b） ChOA-ELM model determines the water content of instance training samples and test samples. The accuracy rates are respectively 97.5% and 100% respectively， which are higher than that of the ChOA-SVM and ChOA-BP models， and have better judgment accuracy and generalization ability; c） ChOA can effectively optimize ELM input layer weights and hidden layer bias values. It is feasible to use ChOA-ELM to determine the water richness of coal roof and floor formations. The model， ELM weights and bias value optimization methods can provide references for related judgments research.

Key words： water abundance; grading judgment; extreme learning machine; chimp optimization algorithm; simulation; parameter optimization

1 研究背景

科学合理判定煤层顶底板地层富水性分级，对于全面掌握煤层顶底板地层富水性分布情况，科学提出风险预防措施，减轻或消除矿井突水隐患以及有效保护地下水资源均具有重要意义。煤层顶底板地层富水性分级判定方法根据数据来源一般分为物探法和多因素综合分析法，物探法存在工作量大、费用高且控制范围有限等问题，而多因素综合分析法应用较为广泛[1]。目前，用于富水性分级判定的多因素综合分析法有主成分分析法[2]、BP神经网络法[3]、支持向量机（SVM）法[4]、集对分析-可变模糊集法[1] 等。极限学习机（ELM）是近年来兴起的一种隐层前馈神经网络（SLFNs）学习算法，具有预测精度高、学习速度快、参数少等优点，已在各行业得到应用，但鲜见于富水性判定研究。相比BP神经网络、SVM等，ELM模型不但克服了传统前馈神经网络反复迭代调整权重参数的缺点，而且同时兼顾模型精度和学习效率[5]。然而，由于ELM输入层权值和隐含层偏值的随机选取，使得模型存在稳定性能差、预测精度低等问题，因此对ELM输入层权值和隐含层偏值进行优化显得非常重要。目前，用于优化ELM参数的智能方法有遗传算法（GA）[6]、粒子群优化（PSO）算法[7]、生物地理学优化（BBO）算法[8]、花粉算法（FPA）[9] 、共生生物搜索 （SOS）算法[10]等。

为提高煤层顶底板地层富水性分级判定精度，有效解决ELM输入层权值和隐含层偏值优化问题，本文研究提出一种基于黑猩猩优化算法（ChOA）与ELM相融合的富水性分级判定方法。选取4个标准测试函数在5维、10维、30维、50维、100维条件下对ChOA进行仿真测试，仿真结果与粒子群优化（PSO）算法、人工蜂群（ABC）算法作对比，以验证ChOA在不同维度条件下的寻优精度和全局搜索能力;基于煤层顶底板地层富水性判定因子和判定分级构建ELM模型，利用ChOA优化ELM输入层权值、隐含层偏值，建立ChOA-ELM富水性分级判定模型，并构建ChOA-SVM、ChOA-BP模型作对比;通过龙固煤层顶底板地层富水性分级判定实例对ChOA-ELM、ChOA-SVM、ChOA-BP模型进行检验，验证ChOA-ELM模型用于富水性分级判定的可行性。

2 ChOA-ELM判定模型

2.1 黑猩猩优化算法（ChOA）

2.1.1 ChOA数学描述

黑猩猩优化算法（ChOA）是M. Khishe等人于2020年根据黑猩猩群体狩猎行为提出的一种新型元启发式优化算法。ChOA通过模拟攻击黑猩猩、驱赶黑猩猩、拦截黑猩猩和追逐黑猩猩4类黑猩猩协同狩猎行为来达到求解问题的目的。与其他算法相比，ChOA具有收敛速度快、寻优精度高等特点。

参考文献[11]，对ChOA数学描述简述如下。

（1）驱赶和追逐猎物。在黑猩猩狩猎过程中，通常根据黑猩猩个体智力和性动机来分配狩猎职责。任何黑猩猩均可随机改变其在猎物周围空间中的位置，数学描述为

式中：d为黑猩猩与猎物间距;t为当前迭代次数;xprey（t）为猎物位置向量;xchimp（t）为黑猩猩位置向量;a、m、c为系数向量，a=2fr1-f，c=2r2，m=Chaotic_value（基于混沌映射的混沌向量），f为迭代过程中从2.0非线性降至0，r1、r2为[0，1]范围内的随机向量。

（2）攻击方式。黑猩猩能够探查猎物位置（通过驱赶、拦截和追逐），然后包围猎物。狩猎过程通常由攻击黑猩猩进行，驱赶黑猩猩、拦截黑猩猩和追逐黑猩猩参与狩猎过程。4类黑猩猩通过下式更新其位置，其他黑猩猩根据最佳黑猩猩位置更新其位置，猎物位置由最佳黑猩猩个体位置估计。数学描述为

式中：dAttacker、dBarrier、dChaser、dDriver分别为当前攻击黑猩猩、拦截黑猩猩、追逐黑猩猩、驱赶黑猩猩与猎物的间距;xAttacker、xBarrier、xChaser、xDriver分别为攻击黑猩猩、拦截黑猩猩、追逐黑猩猩、驱赶黑猩猩相对于猎物的位置向量;a1～a4、m1～m4、c1～c4分别为攻击黑猩猩、拦截黑猩猩、追逐黑猩猩、驱赶黑猩猩系数向量;x1、x2、x3、x4分别为攻击黑猩猩、拦截黑猩猩、追逐黑猩猩和驱赶黑猩猩位置更新向量;x为其他黑猩猩位置向量。

（3）攻击和寻找猎物。在狩猎最后阶段，一方面黑猩猩根据攻击者、驱赶者、拦截者和追逐者位置更新位置，并攻击猎物;另一方面黑猩猩通过分散寻找猎物显示探查过程，即ChOA全局搜索。

（4）社会动机。社会动机（性爱和修饰）会导致黑猩猩放弃其狩猎职责，这一行为有助于ChOA在求解高维问题时克服陷入局部最优和收敛速度慢等缺点。在优化过程中，通过50%的概率选择黑猩猩正常位置更新或通过混沌模型进行位置更新。数学模型表示为

式中：μ为[0，1]范围内的随机数。

2.1.2 ChOA仿真验证

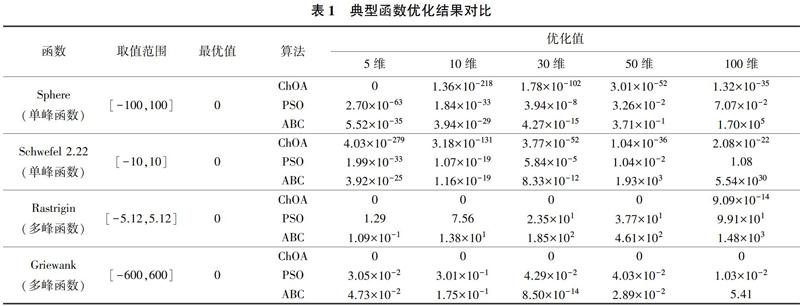
为验证ChOA在不同维度条件下的寻优能力，选取Sphere、Schwefel 2.22、Rastrigin、Griewank 4个典型测试函数，在5维、10维、30维、50维、100维条件下对ChOA进行仿真验证，并与PSO算法、ABC算法的仿真结果进行比较。其中，单峰函数主要测试ChOA的寻优精度，多峰函数主要测试ChOA的全局搜索能力，并利用20次寻优平均值对ChOA寻优性能进行评估，见表1。实验参数设置如下：ChOA、PSO算法、ABC算法最大迭代次数tmax=3 000，种群规模N=100。其中PSO算法惯性权重最大值wmax、最小值wmin分别取0.9和0.3，ABC算法局部循环次数lc=60，其他参数采用各算法默认值。

（1）对于單峰函数Sphere，ChOA算法在5维条件下20次寻优均获得了理论最优值0，在10维、30维、50维、100维条件下寻优精度较PSO、ABC算法提高33个数量级以上;对于单峰函数Schwefel 2.22，ChOA在不同维度条件下寻优精度较PSO、ABC算法提高22个数量级以上。说明对于单峰函数，ChOA具有较好的寻优精度。

（2）对于典型易陷入局部极值多峰函数Rastrigin，ChOA算法在5维、10维、30维、50维条件下20次寻优均获得了理论最优值0，在100维条件下寻优精度较PSO、ABC算法提高15个数量级以上;对于多峰多模态函数Griewank，ChOA在不同维度条件下20次寻优均获得理论最优值0。说明对于多峰函数，ChOA具有较好的全局搜索能力。

可见，ChOA在不同维度条件下对上述4个测试函数均具有较好的寻优精度和全局搜索能力，寻优效果优于PSO、ABC算法。

2.2 极限学习机（ELM）

极限学习机（ELM）是一种单隐层前馈神经网络的新型学习算法，由输入层、隐含层和输出层组成。与传统神经网络相比较，ELM具有计算速度快、泛化性能好、隐含层无须调节等优点。假设K个输入样本（Xi，Yi），其中输入变量有s维，ELM模型具有I个隐层节点和M个输出层节点，激励函数为g（X），ELM的输出可表示为[6，12-13]

式中：wi为输入层到第i个隐含层节点的输入权值;bi为第i个隐含层节点的偏值;βi为连接第i个隐含层节点的输出权值。

若ELM能以零误差接近K个样本，则存在wi、bi、βi使式（8）成立：

上式简化为

式中：H为隐含层输出矩阵。

当g（X）无限可微时，只需随机给出输入权值和偏值，则隐含层输出矩阵H固定不变，那么ELM的训练过程可看作求解线性方程Hβ=Y关于的最小二乘解：

式中：H+为矩阵H的Moore-Penrose广义逆矩阵;T为网络输出矩阵;为输出权值矩阵。

ELM算法的训练步骤：①随机产生ELM输入层权值wi和隐含层节点偏值bi（i=1，2，…，I）;②选择激励函数g（X），计算隐含层输出矩阵H;③计算隐含层节点与输出层节点之间的连接权值。

2.3 判定模型的建立及实现步骤

ChOA优化ELM输入层权值和隐含层偏值的基本思想：将ELM输入层权值和隐含层偏值映射为ChOA黑猩猩位置，设计ChOA-ELM模型适应度函数，将ChOA-ELM模型最优化问题转化为求解适应度函数全局最小时对应的攻击黑猩猩位置，即全局最优解。根据攻击黑猩猩位置与ELM输入层权值和隐含层偏值映射关系，即可得到ELM最优输入层权值和隐含层偏值[14]。具体实现步骤如下。

（1）确定富水性分级判定影响因子，根据水文地质专家对煤层顶底板地层富水性分级判定结果构建ELM模型，利用ChOA优化ELM输入层权值和隐含层偏值，建立ChOA-ELM富水性分级判定模型，合理划分训练样本和检验样本，利用训练样本对ChOA-ELM模型进行训练。

（2）选用训练样本均方误差作为优化目标函数：

式中：j为第j个训练样本富水性实际分级;Mj为第j个训练样本富水性判定分级;k为训练样本数;w为ELM输入层权值;b为隐含层偏值。

（3）设置ChOA种群规模N，最大迭代次数tmax，初始化黑猩猩种群xl（l=1，2，…，N）和参数f、a、m、c。

（4）令当前迭代次数t=1，计算每只黑猩猩的位置，将黑猩猩随机分成攻击、驱赶、拦截和追逐4类。

（5）计算每只黑猩猩个体适应度值，确定攻击黑猩猩、驱赶黑猩猩、拦截黑猩猩和追逐黑猩猩的位置。其中x1為最佳位置，x2为第二佳位置，x3为第三佳位置，x4为第四佳位置。

（6）对于各类黑猩猩，利用分类策略更新f、m、c，计算a、d。若μ<0.5且|a|<1，则利用式（2）更新当前黑猩猩位置，若μ<0.5且|a|>1）则随机选择黑猩猩位置;若μ>0.5，则利用式（6）更新当前黑猩猩位置。

（7）令t=t+1，判断t是否等于tmax。若是，输出攻击黑猩猩位置x1，即算法最优解;否则转至步骤（5）。

（8）输出全局攻击黑猩猩位置x1，即ELM输入层权值和隐含层偏值矩阵。

3 实例分析

（1）研究区概况与数据来源。龙固煤矿位于山东省巨野县城西13～28 km，东起田桥断层，西至煤系地层底界露头，南起邢庄断层、刘庄断层，北至陈庙断层及第一勘探线，南北长约12 km，东西宽约15 km，面积约180 km2。依据文献[4]，龙固煤矿3号煤层底板富水性与3号煤层顶板至山西组顶板砂岩总厚、3号煤层顶板至山西组顶板范围内砂/泥比等6个因子有关，见表2。为便于计算机处理分析，将顶、底板砂岩富水性由Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ级转化为5、4、3、2、1级，数字越大表明富水性越强。本文利用表2中前40组数据作为训练样本，后9组数据作为检验样本。

（2）参数设置。设置ChOA最大迭代次数tmax=200，种群规模N=50;ChOA-ELM模型激活函数选择sin函数，输入层权值和隐含层偏值搜索范围[-1，1]，隐含层数设置为5。参考文献[14]，ChOA -SVM模型惩罚因子C、核函数参数g搜索空间均设置为[10-3，102]，不敏感系数ε搜索空间设置为[10-4，10-1];ChOA-BP模型权阈值参数搜索空间设置为[-1，1]，网络结构设置为6-5-1，隐含层传递函数、输出层传递函数和训练函数分别选择logsig、purelin和traingdx，训练次数设置为500，期望误差设置为0.01。所有输入数据均进行归一化处理。

（3）判定结果及对比分析。基于ChOA-ELM、ChOA-SVM、ChOA-BP模型对3号煤层底板砂岩富水性分级进行训练及判定，小数部分采用四舍五入法输出判定结果。利用判定准确率（%）、训练样本适应度min f对各模型性能进行评价，结果见表3;各模型判定结果及判定效果见图1。

由表3及图1可知：

（1）ChOA-ELM模型对实例训练样本和检验样本富水性分级判定准确率分别为97.5%、100%，适应度min f为0.069 64，判定准确率高于ChOA-SVM、ChOA-BP模型，而适应度min f小于ChOA-SVM、ChOA-BP模型。表明ChOA能有效优化ELM输入层权值和隐含层偏值，ChOA-ELM模型具有较好的判定精度和泛化能力，将ChOA-ELM模型用于富水性分级判定是可行的。

（2）ChOA-ELM模型对训练样本富水性分级仅有1个误判，检验样本富水性分级没有误判;ChOA-SVM模型对训练样本、检验样本分别有2个、1个误判;ChOA-BP模型对训练样本、检验样本各有1个误判。ChOA-ELM模型对训练样本、检验样本具有更好的判定效果，与ChOA-SVM、ChOA-BP模型相比，更接近3号煤层底板富水性实际分级。

4 结 论

为提高煤层顶底板地层富水性分级判定精度，有效解决ELM输入层权值和隐含层偏值优化问题，研究提出ChOA-ELM判定模型，利用龙固煤层顶底板地层富水性分级判定实例对ChOA-ELM模型进行检验，并构建ChOA-SVM、ChOA-BP模型作对比，得出以下结论。

（1）ChOA在5维、10维、30维、50维、100维条件下寻优效果优于PSO、ABC算法，具有较好的寻优精度和全局搜索能力，将ChOA用于ELM输入层权值和隐含层偏值寻优是可靠的。

（2）ChOA-ELM模型对实例训练样本和检验样本富水性分级判定准确率分别为97.5%、100%，判定精度高于ChOA-SVM、ChOA-BP模型，具有较好的判定精度和泛化能力，将ChOA-ELM模型用于煤层顶底板地层富水性分级判定是可行的。

参考文献：

[1] 韩承豪，魏久传，谢道雷，等.基于集对分析-可变模糊集耦合法的砂岩含水层富水性评价：以宁东矿区金家渠井田侏罗系直罗组含水层为例[J].煤炭学报，2020，45（7）： 2432-2443.

[2] 王颖，韩进，高卫富.基于主成分分析法的奥灰富水性评价[J].中国科技论文，2017，12（9）：1011-1014.

[3] 宫厚健，刘守强，曾一凡.基于BP神经网络的含水层富水性评价研究[J].煤炭技术，2018，37（9）：181-182.

[4] 卫文学，韩进，施龙青，等.现代数据分析在矿山涌水预测中的应用[M].北京：煤炭工业出版社，2015：61-64.

[5] 盛晓晨，史旭东，熊伟丽.改进粒子群优化的极限学习机软测量建模方法[J].计算机应用研究，2020，37（6）：1683-1687.

[6] 陈艳茹.基于遗传算法和极限学习机的智能算法在基坑变形预测中的应用[J].隧道建设（中英文），2018，38（6）：71-77.

[7] 范君，王新，徐慧.粒子群优化混合核极限学习机的构造煤厚度预测方法[J].计算机应用，2018，38（6）：1820-1825.

[8] 刘科，李军.基于BBO-ELM方法的网络视频流量预测仿真研究[J].计算机应用研究，2018，35（6）：1728-1732.

[9] 邵良杉，李臣浩.基于改进花粉算法的极限学习机分类模型[J].计算机工程与应用，2020，56（1）：172-179.

[10] 蔡改貧，赵小涛，张丹荣，等.基于ASOS-ELM的湿式球磨机负荷软测量方法[J].振动、测试与诊断，2020，40（1）：184-192，211.

[11] KHISHE M，MOSAVI M R. Chimp Optimization Algorithm[J/OL]. Expert Systems with Applications，2020，149：113338.[2021-12-12].https：//doi.org/10.1016/j.eswa.2020.113338.

[12] 殷豪，董朕，孟安波.基于结合混沌纵横交叉的粒子群算法优化极限学习机的短期负荷预测[J].计算机应用研究，2018，35（7）：174-177.

[13] 左智科，李一龙.改进的TLBO及其在自来水供水量预测中的应用[J].人民黄河，2021，43（2）：84-87.

[14] 李代华，崔东文.基于PCA-MPA-ANFIS模型的年径流预测研究[J].水电能源科学，2020，38（7）：24-29.

【责任编辑 张华兴】