浅水方程源项处理的研究进展
许仁义 汪凌翔 王远见 方浩川 王俊贤 戴惠东


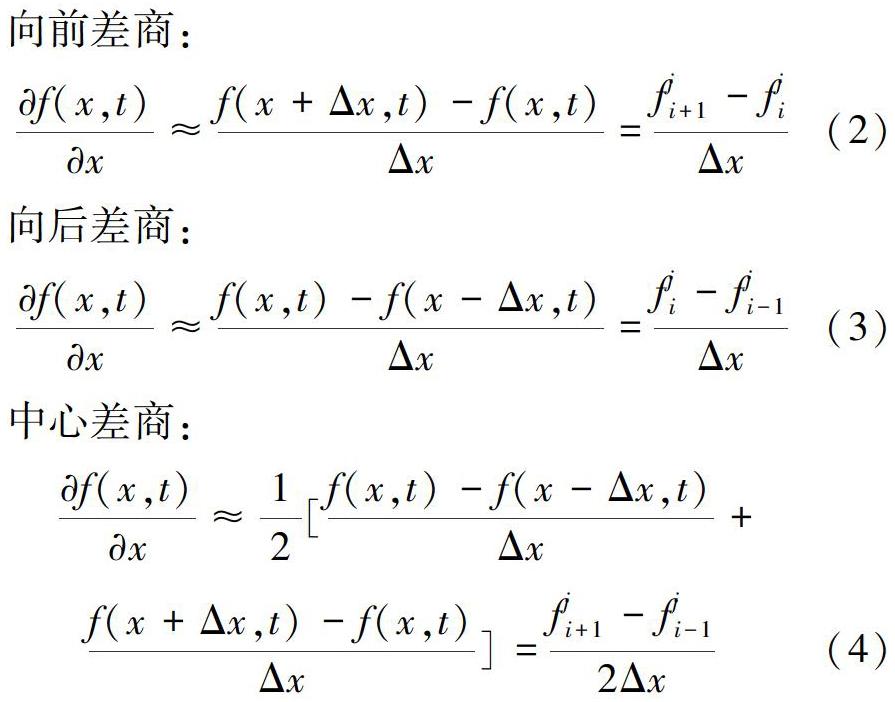
摘 要:浅水方程由纳维-斯托克斯方程推导而来,是一种描述具有自由表面的浅水体在重力作用下流动的数学模型。实际浅水流动不可能是完全理想的情况,必须考虑底坡和摩阻等源项的存在,它们影响计算的稳定性和精确性,如果处理不当还会造成格式的不和谐,因此源项处理是求解浅水流动方程的关键,也是国内外学者研究的一个重要方向。介绍目前求解浅水方程存在的4个主要困难,介绍浅水方程的各种离散方法以及优缺点,阐述源项处理的重要性和源项的分类,回顾和总结国内外处理源项的方法以及目前存在的困难。根据目前的研究进展,源项处理依旧有广阔的研究前景,如何平衡好源项处理方法的正效应和负效应是一个值得研究的课题。
关键词:浅水方程;源项处理;和谐性;有限体积法;不规则地形
中图分类号:TV131 文献标志码:A
doi:10.3969/j.issn.1000-1379.2021.07.007
引用格式:许仁义,汪凌翔,王远见,等.浅水方程源项处理的研究进展[J].人民黄河,2021,43(7):35-40,83.
Abstract: The shallow water equation, derived from the Navier-Stokes equation is a mathematical model to describe the flow of shallow water with a free surface under the action of gravity. Actual shallow water flow cant be a perfectly ideal situation, bottom slope and friction must always be considered such as the existence of the source term. It affects the calculations stability and precision, if handles not properly it will cause disharmony in the format. Thus, the source term processing is the key to solve the shallow water flow equation and also is an important direction in the research of scholars at home and abroad. This paper introduced four main difficulties in solving shallow water equation and various discrete methods of shallow water equation as well as their advantages and disadvantages, expounded the importance of source term treatment and the classification of source term and reviewed and summarized the methods of source term treatment at home and abroad as well as the existing difficulties. Finally, according to the current research progress, it put forward that the source term treatment still had a broad research prospect and how to balance the positive and negative effects of source term treatment would be a worthy topic to be studied.
Key words: shallow water equation; source term processing; well-balance; finite volume method; irregular terrain
水力學中的浅水是指水深尺度远小于平面尺度且垂向流速小的水流[1],人们关心的溃坝问题、水环境污染问题、潮汐和涌浪等都可以用浅水流动描述,而浅水方程是描述各类浅水流动的数学形式。如今,随着计算机性能大幅提升,浅水数值模拟以其无可替代的优势开始广泛应用于河道、河口、水库以及近海水域等环境。浅水方程是一种非线性双曲型方程,如何更加精确且高效地求解是一个值得研究的课题,因此衍生出许多离散方式。由于现实环境的复杂性,为了得到更加真实的数值结果,必须考虑源项的存在,因此探求源项处理方法成为了许多学者研究的方向。
1 控制方程
控制方程为一维浅水方程守恒形式,满足静压假定。
式中:守恒变量向量U=hhu;通量向量F(U)=huhu2+12gh2;源项向量S(U)=Sb+Sf+Sw+Sc,如果忽略表面风应力和柯氏力,则S(U)=Sb+Sf=0gh(-Sbx-Sfx),其中Sbx=zx;Sfx为沿x方向的阻力;Sb、Sf、Sw、Sc分别为底坡源项、摩阻源项、表面风应力、柯氏力;z为河床曲面高程;u为x方向的平均流速;h为水深;g为重力加速度。
2 求解浅水方程存在的困难
浅水方程属于非线性双曲型偏微分方程,满足质量守恒、动量守恒和能量守恒,这种物理量守恒的方程也可以被称为双曲守恒方程[2]。求解非线性偏微分方程组十分困难,很难获得解析解,为了得到更精确的数值解,一般有两种办法:一种是提高计算机的算力,另一种就是不断改良数值方法、提高计算精度和计算效率。
目前数值求解浅水方程这类双曲守恒方程存在以下困难:
(1)解的间断。扰动波传播速度有限,可能产生间断,在间断处的导数无意义,无法求解微分方程。引入“弱解”的概念[3],即弱解在间断点外的其他点上满足微分方程,在间断点上满足一组跳跃条件(Rankine-Hugoniot条件)[4],它能够将间断点两侧的水力要素联系起来。
(2)弱解的非唯一性。浅水方程在推导的时候就已经做出前提假设,同时忽略了某些物理量带来的影响,这就会导致模型与实际情况存在偏差[5]。
(3)解的稳定性。更高的模型精度以及求解时存在的误差容易引起数值振荡,因此需要优化和改善高精度计算方法的数值振荡问题[6]。
(4)源项的处理。浅水方程如果不包含源项,则为齐次浅水流动方程,这类方程由于略去了地形变化、摩阻等计算项,形式上与空气动力学中使用广泛的欧拉方程类似[7],因此早期研究阶段借鉴了空气动力学中的求解方法[8]。比如基于近似Riemann解Godunov格式的Roe方法[9]就是一种最初用于空气动力学的方法。但在水流數值模拟中,计算区域往往都是非平面的,对源项简单处理会导致计算结果的不和谐,即静水条件下,计算趋于稳定后,无法满足流速为零、水位为常数的结果[10]。下面将着重阐述源项的处理方法。本文提出了齐次浅水方程的解决方法,而非齐次浅水方程的问题有待解决,比如含源项的非齐次浅水方程的大时间步长格式现在仍未得到解决[11]。
3 离散方法
3.1 特征线法(MOC)
特征线法是利用特征线以及特征相容关系进行离散得到数值解的方法,在计算机出现以前这还是CFD手工算法之一。它的物理意义明确,计算精度较高,但是不适合带有源项的非齐次方程,目前很少直接采用该方法[12]。
3.2 有限差分法(FDM)
有限差分法就是在计算域上将原来控制方程中网格节点的微分项直接用差商近似代替,然后进行泰勒级数展开,可以在每个网格节点处得到离散方程,因此该方法简单成熟,可以构造高精度的格式,但是对复杂网格的适应性不佳[13]。
对方程离散时,常采用向前差商、向后差商和中心差商等格式。
向前差商:
3.3 有限元法(FEM)
有限元法基本思想是将一个求解区域划分成许多微小单元,根据极值原理,把所有微小单元极值之和作为总体的极值。由于微小单元可以是各种形状,因此网格划分较灵活。这种方法守恒性好,但是在处理复杂方程时比较困难[13]。在推导有限元格式时一般会采用加权余量法,它的基本思想就是选定一个试探函数φi代替原方程中的待求函数,此时必然会产生误差,可以称为余量R,然后在计算域Ω内找到n个线性无关的权函数δWi(i=1,2…,n),满足
这就意味着余量R在加权平均的意义上为零。
3.4 有限体积法(FVM)
有限体积法基本思路是构造一系列控制体,对控制体中的微分方程积分,控制体内又满足总质量、总动量和总能量守恒,因此方程守恒性好,可以处理复杂网格计算问题,结合了FDM和FEM的优点[12],也是目前使用最广泛的方法,本文所讨论的源项处理大部分也是基于此方法。
在网格单元Vi内对式(1)积分:
通过Gauss-Green公式将式(6)转化为沿单元边界的线积分,可以写成
式中:ΔVi为网格单元的面积;Vi为网格单元的边界;n为单元边线外法线的单位向量;l为单元边长;S为网格单元源项的积分值。
3.5 间断有限元法(DG)
间断有限元法很好地结合了FDM、FEM和FVM的长处,具有精度高、守恒性好和易于处理复杂网格的特点[14-15],但是计算量大、程序设计较复杂且难以处理间断问题[2],因此目前一般都在光滑处用此方法。在式(5)的基础上,将试探函数φi作为权函数δWi:
3.6 粒子法(SPH)
粒子法是最近发展起来的一种无网格方法,它的核心是一种插值方法,可以处理复杂的外形,但是精度并不易提高[16]。
4 源项的处理
浅水方程求解过程中,源项处理是数值模拟成败的关键,处理不当可能导致在巨大的计算量下结果依旧失真和失稳,同时破坏求解格式和谐性,因此学者们提出了广泛的解决方法。源项可以分为底坡引起的底坡源项、底摩擦引起的摩阻源项、地球自转引起的柯氏力和表面风应力。李文俊等[17]建立的二维水沙模型充分考虑了以上4个源项的影响,在模拟实际的大潮中,模拟结果与实测值能良好吻合。下面重点阐述对方程影响最大的两个源项。
4.1 底坡源项的处理
Zhao等[18]、谭维炎等[19]在20世纪90年代把斜底地形简化为多级阶梯、每个阶梯视为平底,不需要考虑底坡的影响,可以用齐次浅水方程计算。这样做会产生两类误差:一类是采用平均底高和平均水力要素代替实际情况导致,可以通过减小阶梯的长度来减少误差;另一类是计算通量时相邻平底模型中法向动量通量的对流项出现变化所致,可以通过加修正值保持原值不变。此方法更适合于地形变化较缓的区域。
Bermudez等[20]在同时期提出用迎风格式处理含有源项的双曲守恒方程,并对Van Leer的Q格式进行了扩展。与以前的方法相比,此方法得到的数值解在稳定性和精度上有明显的提升。应用到浅水方程后,该方法在处理源项时并不能始终保证数值格式拥有良好的性能。后来Bermudez将同样的思想用于解决更贴近实际的二维浅水问题。Vazquez[21]、Brufau等[22]在此基础上又改进了对地形等源项的模拟方法,使其能够适应复杂多变的水流环境,但在求解法向通量时只验证了Roe格式有较好的性能。
Rogers等[23-24]提出的数值平衡法用确保质量和动量守恒的代数方式拆分底坡源项。这种方法应用到浅水方程后消除了近似解算器中的数值振荡,但是由于没有考虑静水压力项的非线性分布,因此底坡源项和通量项的误差不可避免,只要水位不为零就会出现虚假流动。
Leveque[25]提出了一种水波传播算法,在每个计算单元内部人为地引入一个不连续量来处理源项。该方法适用于准稳态条件,但在预测含有冲击的跨临界流动时无法带来稳定的数值结果。Kurganov等[26]将中心迎风格式(CU)推广到浅水方程组,提出了一种适用于复杂地形的自适应算法。但是这些方法在处理循环流时会出现巨大的数值耗散。
Zhou等[27]先推导了适用于均质无黏方程的深度梯度法(DGM),为解决这种方法受地形影响很大的问题,又通过水位重构的方法得到了水面梯度法(SGM),这种分段线性重建的方法在没有底坡源项的时候与DGM相同,最后用HLL-Riemann解算器进行了验证。水面梯度法(SGM)更适合在结构网格下的水流计算,原因是在非结构网格上Bermudez提出的C-property守恒概念并不成立。类似的,Wang等[28]采用通量分裂修正技术分解源项,以满足C-property守恒,在光滑区域保持其原始高阶精度,并在强间断附近保持基本上无振荡的性质。
潘存鸿等提出了水位方程法(WLF),该方法将浅水流动方程中水深变量替换为水位,处理后用经典方法求Riemann解,这在本质上与Zhou等提出的SGM方法是相同的,只是WLF法更易理解,更能说明理论上SGM法的误差性质和误差大小的由来。其中底坡源项在Riemann问题中的离散形式必须与压力梯度项的离散形式保持一致,且水深也要采用Riemann解,不然解的和谐性将无法保证。潘存鸿用WLF法建立Godunov格式求解一维浅水方程的Riemann问题,并推广到求解二维浅水方程的Riemann问题[29],该方法保持了计算的通用性、和谐性和高分辨率。
Mohammadian等[30]提出用修正水流对底坡源项进行相容离散化,由于在所提出的方法中,不需要对源项进行额外的迎风求解或Riemann求解,而是直接对源项离散,因此不光能采用Roe方法,还可以采用已有的激波捕捉方法,如CU方法、HLL方法、HLLC方法[31]等。與现有的许多格式不同,该方法易于在非结构网格上实现,并能灵活处理不规则边界和局部网格重构问题。作者通过一系列算例证明提出的方法能够准确地模拟复杂地形下的各种临界流和跨临界流动。
Smolarkiewicz等[32]采用MPDATA法(multidimensional positive definite advection transport algorithm)处理带有底坡源项的方程。MPDATA法原本是一种处理大气平流的方法,经过很多学者的不懈努力,其已经有能力解决复杂的流体问题。Jenny等[33]提出一种改进的解算器Rankine-Hugoniot-Riemannsolver(简称RHR解算器),它的基本思想是将源项视为不连续项,得到单元内的双曲条件,就可以应用Riemann不变量的思想来特征处理源项。RHR解算器所得结果比传统的Riemann解算器得到的结果更精确,在处理更高维度的情况时也具有较好表现。
王志力等[34]提出了特征分解底坡源项来平衡界面通量的方法。相比于简单处理源项,该方法可以保证格式的和谐性。王昆等[10]把底坡源项表示成某个矩阵的散度形式,计算量小,概念也简单,为了保证格式的和谐性,还对两个相邻单元水深使用均方根形式以抵消数值通量项。周浩澜等[1]用静水重构法重构后的水深替换原水深,也保证了计算格式的和谐性。魏红艳等[35]也采用了类似的方法。于守兵[36]提出的静水压力项和底坡项的积分平衡法,可以准确计算两者的值并保持严格的平衡,不产生虚假流动。
求解这种双曲问题常用基于有限体积法的数值格式,其目的是将区域预先离散成体积单元并在这些单元内集成信息和控制方程来提供问题的数值解[37]。用有限体积法处理浅水方程,把方程中水位梯度项分解成静水压力梯度项和底坡源项,静水压力随着水深的增大是非线性变化的,因此在静水中底坡源项和静水压力梯度项往往难以相互抵消,这就是产生虚假流动的原因。为了避免出现这种情况,学术界主要存在两种方法:一种是通过对模型的修正消去底坡源项,比如谭维炎等[19]提出的平底模型;另一种是对底坡源项进行分解或者改造,使它能够与静水压力梯度项相互抵消,比如Mohammadian等[30]、潘存鸿等[38]、王志力等[34]提出的方法。
网格的选择也对源项处理有着直接影响,比如在非结构三角形网格上就比四边形网格更难满足和谐性要求。王昆等[10]、宋利祥等[39]在三角形网格下建立了和谐性离散格式,并用算例验证了其适用性。
使用有限体积法时,两个单元的界面处为一个局部间断,底坡源项此时就变成阶梯间断,有限体积法在这里需要求解阶梯Riemann问题(Step Riemann Problem,SRP)。尽管这不是一个新问题,也有很多研究成果,但仍然是有争议的,其研究的方法大致可分为两类:一类是使用质量守恒和能量守恒的方法,Alcrudo等[40]和Bukreev等[41]认为必须采用这种方法,因为在SRP中间断处的河床底坡趋向于无穷大,所以此时依据动量守恒推导出的SWE没有意义,然而众所周知的是在阶梯处发生流动的过程中能量其实并不守恒,由于湍流的存在会导致能量耗散,因此这两人的理论基础存在瑕疵。Gallouet等[42]、Seguin等[43]和Andrianov[44]认为既然间断处的接触间断是驻波,那么在特征空间里Riemann不变量守恒,这必然使得质量和能量守恒,然而这也是从数学观点去分析这个问题,在物理上或者说在实际工况中并不是这样。还有一类是使用质量守恒和动量守恒的方法,比如Bernetti等[45]在其研究成果中把能量守恒仅仅作为一个约束条件来检验所得的结果是否正确。Rosatti等[46]通过研究得出,当上游河床高于下游河床时,目前所得出的研究成果都是错误的,这个问题至今未得到解决。
4.2 摩阻源项的处理
对于不规则地形的浅水模拟,在局部陡峭的底坡可能会出现水深过小而流速很大的情况,这时会引起摩阻源项的刚性问题[47]。很多基于无结构网格的数值方法都采用显式,显式在程序的编写上相对简单,但是局限性也很大[48]。若采用显式数值方法离散摩阻源项,可能会出现明显的物理错误,比如出现虚假流动、负水深等[1],或是影响时间步长、降低计算效率[39]。隐式在计算稳定性上要优于显式,且不受Courant的限制,可以与自适应网格技术结合。Michel等[49]在几个溃坝数值模拟中对比了显式处理和隐式处理的差异,总体来说,隐式处理更接近真实情况,比如在模拟干湿边界时显式处理易出现伪振荡,而隐式处理并未出现。因此,一般采用隐式或者半隐式处理摩阻源项。
王党伟等[50]、王鑫等[51]用三阶龙格-库塔法处理源项,并对摩阻项采用自适应步长法进行处理。Yoon等[52]通过算子分裂法完全隐式处理摩阻项,以防止干燥区附近小水深引起的数值不稳定性。Martinez[53]采用半隐式离散方法,Hou等[54]提出了一种基于隐式概念的方法,并且能够集成到常用的显式方法中,避免了冗余迭代,并能够使用更大的计算时间步长,从而提高了编程和计算的效率。Cea等[55]、Singh等[56]将摩阻源项用速度的乘积表示以获得显式格式,虽然可以有效避免由刚性问题引起的数值不稳定,但是流动通常无法维持稳态,导致模拟结果失真。Xia等[57]提出一种在有限体积法下的新的隐式解法,可以同时保证数值稳定性和模拟的准确性,该解法可以不使用迭代法直接计算摩擦项,而且理论上还可以用于其他数值方法,如有限差分法和有限元法。
5 总结与展望
浅水方程的源项处理问题在经过国内外学者的潜心研究下取得了丰硕的成果,未来继续改进和开发更简单有效且具有更好收敛性的格式将会是一个趋势。应该注意到有些源项问题至今没有得到解决,比如当上游河床高于下游河床时,目前所有的局部阶梯Riemann问题的求解方法都是错误的,需要通过数值试验和物理试验的方法深入研究才能找到准确的答案,这也会是将来浅水方程源项问题研究的方向。对于新的數值格式,比如大时间步长格式,传统的源项处理方法不再适用,新格式的源项处理方法也是一个值得探索的研究方向。
浅水方程作为非线性的偏微分方程组,现在并没有解析解,所有解决的方法都是数值近似解,目前所有研究都是让数值解尽可能地逼近实际情况,而任何方法都不是完美的,每一种数值方法的改进都会带来一定的负效应,需要权衡这种改进与负效应在实际工程中的应用。因此,源项的数值处理方法还有很大的发展空间。
参考文献:
[1] 周浩澜,陈洋波,任启伟.不规则地形浅水模拟[J].水动力学研究与进展(A辑),2010,25(5):594-600.
[2] 潘存鸿.浅水间断流动数值模拟研究进展[J].水利水电科技进展,2010,30(5):77-84.
[3] SINGER T, VESTBERG M. Local Boundedness of Weak Solutions to the Diffusive Wave Approximation of the Shallow Water equations[J].Journal of Differential Equations,2019,266(6):3014-3033.
[4] ZIJLEMA M. The Role of the Rankine-Hugoniot Relations in Staggered Finite Difference Schemes for the Shallow Water Equations[J].Computers and Fluids,2019,192(10):104274.
[5] BUCKMASTER T, VICOL V. Nonuniqueness of Weak Solutions to the Navier-Stokes Equation[J].Annals of Mathematics,2019,189(1):101-144.
[6] DU H, LIU Y, LIU Y, et al. Well-Balanced Discontinuous Galerkin Method for Shallow Water Equations with Constant Subtraction Techniques on Unstructured Meshes[J].Journal of Scientific Computing,2019,81(3):2115-2131.
[7] 汪德爟.计算水力学理论与应用[M].北京:科学出版社,2011:31-36.
[8] TORO E F. Shock-Capturing Methods for Free-Surface Shallow Flows[M]. New Jersey: John Wiley,2001:324-339.
[9] ROE P L. Approximate Riemann Solvers, Parameter Vectors, and Difference Schemes[J].Journal of Computational Physics,1997,135(2):250-258.
[10] 王昆,金生,马志强,等.基于和谐性离散格式求解带源项的二维浅水方程[J].水动力学研究与进展(A辑),2009,24(5):535-542.
[11] MORALES M, LACASTA A, MURILLO J, et al. A Large Time Step Explicit Scheme (CFL>1) on Unstructured Grids for 2D Conservation Laws: Application to the Homogeneous Shallow Water Equations[J].Applied Mathematical Modelling,2017,47:294-317.
[12] 王立輝,胡四一.溃坝问题研究综述[J].水利水电科技进展,2007,27(1):80-85.
[13] 刘林,常福宣,肖长伟,等.溃坝洪水研究进展[J].长江科学院院报,2016,33(6):29-35.
[14] 韩涛,逄勇,李一平,等.基于间断有限元法求解三维NS水流方程[J].人民黄河,2008,30(1):67-69.
[15] CALEFFI V, VALIANI A, LI G. A Comparison Between Bottom-Discontinuity Numerical Treatments in the DG Framework[J].Applied Mathematical Modelling,2016,40(17-18):7516-7531.
[16] 刘谋斌,宗智,常建忠.光滑粒子动力学方法的发展与应用[J].力学进展,2011,41(2):217-234.
[17] 李文俊,张庆河,李龙翔,等.基于无积分节点间断有限元的二维水沙模型:(1)水动力[J].水道港口,2019,40(2):125-134.
[18] ZHAO D H, SHEN H W, III G Q T, et al. Finite-Volume Two-Dimensional Unsteady-Flow Model for River Basins[J].Journal of Hydraulic Engineering,1994,120(7):863-883.
[19] 谭维炎,胡四一.浅水流动计算中一阶有限体积法Osher格式的实现[J].水科学进展,1994,5(4):262-270.
[20] BERMUDEZ A, VAZQUEZ M E. Upwind Methods for Hyperbolic Conservation Laws with Source Terms[J].Computers & Fluids,1994,23(8):1049-1071.
[21] VAZQUEZ C M E. Improved Treatment of Source Terms in Upwind Schemes for the Shallow Water Equations in Channels with Irregular Geometry[J].Journal of computational Physics,1999,148(2):497-526.
[22] BRUFAU P, GARCIANAVARRO P, VAZQUEZCENDON M E. Zero Mass Error Using Unsteady Wetting-Drying Conditions in Shallow Flows over Dry Irregular Topography[J].International Journal for Numerical Methods in Fluids,2004,45(10):1047-1082.
[23] ROGERS B D, BORTHWICK A G L, TAYLOR P H. Mathematical Balancing of Flux Gradient and Source Terms Prior to Using Roes Approximate Riemann Solver[J].Journal of Computational Physics,2003,192(2):422-451.
[24] ROGERS B D, FUJIHARA M, BORTHWICK A G L. Adaptive Q-Tree Godunov-Type Scheme for Shallow Water Equations[J].International Journal for Numerical Methods in Fluids,2001,35(3):247-280.
[25] LEVEQUE R J. Balancing Source Terms and Flux Gradients in High-Resolution Godunov Methods[J].Journal of Computational Physics,1998,146(1):346-365.
[26] KURGANOV A, LEVY D. Central-Upwind Schemes for the Saint-Venant System[J].Mathematical Modelling and Numerical Analysis,2002,36(3):397-425.
[27] ZHOU J G, CAUSON D M, MINGHAM C G, et al. The Surface Gradient Method for the Treatment of Source Terms in the Shallow-Water Equations[J].Journal of Computational Physics,2001,168(1):1-25.
[28] WANG Z, ZHU J, ZHAO N. A New Fifth-Order Finite Difference Well-Balanced Multi-Resolution WENO Scheme for Solving Shallow Water Equations[J].Computers and Mathematics with Applications,2020,80(5):1387-1404.
[29] 潘存鴻,林炳尧,毛献忠.求解二维浅水流动方程的Godunov格式[J].水动力学研究与进展(A辑),2003,18(1):16-23.
[30] MOHAMMADIAN A, ROUX D Y L. Simulation of Shallow Flows over Variable Topographies Using Unstructured Grids[J].International Journal for Numerical Methods in Fluids,2006,52(5):473-498.
[31] 杨峰,倪玉芳,黄卫,等.出山店水库溃坝洪水数值模拟研究[J].人民黄河,2020,42(1):27-31,36.
[32] SMOLARKIEWICZ P K, MARGOLIN L G. MPDATA: a Finite-Difference Solver for Geophysical Flows[J].Journal of Computational Physics,1998,140(2):459-480.
[33] JENNY P, MULLER B. Rankine-Hugoniot-Riemann Solver Considering Source Terms and Multidimensional Effects[J].Journal of Computational Physics,1998,146(2):575-610.
[34] 王志力,耿艳芬,金生.具有复杂计算域和地形的二维浅水流动数值模拟[J].水利学报,2005,36(4):439-444.
[35] 魏红艳,梁艳洁,陈萌,等.基于Roe格式的不规则地形上浅水模拟[J].武汉大学学报(工学版),2019,52(1):7-12,82.
[36] 于守兵.计算二维浅水方程中静水压力项与底坡项的积分平衡法[J].水利水电科技进展,2009,29(4):32-35.
[37] NAVAS A, MURILLO J. Overcoming Numerical Shockwave Anomalies Using Energy Balanced Numerical Schemes. Application to the Shallow Water Equations with Discontinuous Topography[J].Journal of Computational Physics, 2017,340:575-616.
[38] 潘存鸿,林炳尧,毛献忠.一维浅水流动方程的Godunov格式求解[J].水科学进展,2003,14(4):330-336.
[39] 宋利祥,周建中,王光谦,等.溃坝水流数值计算的非结构有限体积模型[J].水科学进展,2011,22(3):373-381.
[40] ALCRUDO F, BENKHALDOUN F. Exact Solutions to the Riemann Problem of the Shallow Water Equations with a Bottom Step[J].Computers and Fluids,2001,30(6):643-671.
[41] BUKREEV V I, GUSEV A V, OSTAPENKO V V. Breakdown of a Discontinuity of the Free Fluid Surface over a Bottom Step in a Channel[J].Fluid Dynamics,2003,38(6):889-899.
[42] GALLOUET T, HRARD J M, SEGUIN N. Some Approximate Godunov Schemes to Compute Shallow-Water Equations with Topography[J].Computers and Fluids,2003,32(4):479-513.
[43] SEGUIN N, CHINNAYYA A, LEROUX A Y. A Well-Balanced Numerical Scheme for the Approximation of the Shallow-Water Equations with Topography: the Resonance Phenomenon[J].International Journal of Finite Volumes,2004,1(1):1-33.
[44] ANDRIANOV N. Performance of Numerical Methods on the Non-Unique Solution to the Riemann Problem for the Shallow Water Equations[J].International Journal for Numerical Methods in Fluids,2005,47(8-9):825-831.
[45] BERNETTI R, TITAREV V A, TORO E F. Exact Solution of the Riemann Problem for the Shallow Water Equations with Discontinuous Bottom Geometry[J].Journal of Computational Physics,2008,227(6):3212-3243.
[46] ROSATTI G, BEGNUDELLI L. The Riemann Problem for the One-Dimensional, Free-Surface Shallow Water Equations with a Bed Step: Theoretical Analysis and Numerical Simulations[J].Journal of Computational Physics,2009,229(3):760-787.
[47] XIA X, LIANG Q, MING X, et al. An Efficient and Stable Hydrodynamic Model with Novel Source Term Discretization Schemes for Overland Flow and Flood Simulations[J].Water Resources Research,2017,53(5):3730-3759.
[48] 唐岳灏.基于无结构化网格浅水方程的隐式解法[J].人民长江,2015,46(5):81-84,96.
[49] MICHEL D V, BERTHON C, CLAIN S, et al. A Well-Balanced Scheme for the Shallow-Water Equations with Topography or Manning Friction[J].Journal of Computational Physics,2017,335:115-154.
[50] 王党伟,陈建国,吉祖稳.不规则地形上浅水模拟平衡性的实现[J].计算力学学报,2012,29(4):604-608,615.
[51] 王鑫,曹志先,岳志远.强不规则地形上浅水二维流动的数值计算研究[J].水动力学研究与进展(A辑),2009,24(1):56-62.
[52] YOON T H, KANG S. Finite Volume Model for Two-Dimensional Shallow Water Flows on Unstructured Grids[J].Journal of Hydraulic Engineering,2004,130(7):678-688.
[53] MARTINEZ V B. A Numerical Technique for Applying Time Splitting Methods in Shallow Water Equations[J].Computers & Fluids,2017,169:285-295.
[54] HOU J, WANG T, LI P, et al. An Implicit Friction Source Term Treatment for Overland Flow Simulation Using Shallow Water Flow Model[J].Journal of Hydrology,2018,564:357-366.
[55] CEA L, BLADE E. A Simple and Efficient Unstructured Finite Volume Scheme for Solving the Shallow Water Equations in Overland Flow Applications[J].Water Resources Research,2015,51(7):5464-5486.
[56] SINGH J, ALTINAKAR M S, DING Y. Numerical Modeling of Rainfall-Generated Overland Flow Using Nonlinear Shallow-Water Equations[J].Journal of Hydrologic Engineering,2014,20(8):172-183.
[57] XIA X, LIANG Q. A New Efficient Implicit Scheme for Discretising the Stiff Friction Terms in the Shallow Water Equations[J].Advances in Water Resources,2018,117:87-97.
【責任编辑 张 帅】

