基于非接触滞环调节器和动态基准调节的自激闭环控制策略

徐立刚，柯光洁，陈乾宏，任小永，张之梁

（南京航空航天大学自动化学院，江苏省南京市 211106）

0 引言

感应式电能传输（inductive power transfer，IPT）技术具有安全、可靠、便捷以及较强的环境适应性等优点，在消费电子、智能家居、电动汽车、植入式医疗设备以及水下、矿井等场合有良好的应用前景［1-4］。实际应用中，IPT系统中耦合机构的原副边完全分离，错位、间隙变化不可避免，由此引起互感、耦合系数等参数的变化。考虑到耦合机构及用电负载的稳态及动态参数的变化，IPT系统需要有可靠、快速的控制方法，适应耦合系数的大范围变化（通常为0.1～0.3）和负载的突变，以获得稳定输出，并具备良好的动态特性。

研究人员提出了不同的控制方案，包括级联DC/DC变换器，应用调宽、移相、脉冲密度调制、On/Off控制［5-12］以及动态调谐［13-14］等，来改善IPT系统的动静态特性。例如，在原边侧级联Buck变换器来调节逆变器的输入电压［5］，基于参数估计，改变逆变桥两桥臂的移相角来调节输出［6］。受限于非接触反馈单元或者动态参数估计方法的响应速度，上述原边侧控制方法的负载动态响应速度较慢。为此，文献［10-11］分别采用后级Boost变换器、脉宽调制（PWM）整流器实现输出稳压。加入后级变换器会增加移动侧的体积和重量，而PWM整流器的引入又会改变等效负载阻抗特性，带来失谐问题。

为了降低控制器设计的复杂度，简化电路结构，研究人员利用非接触谐振变换器固有的增益交点实现恒压或恒流输出［15-16］，并提出了多种非接触自激控制策略。文献［17］针对并/串补偿网络，利用原边并联电容两端电压产生同相的自激驱动信号，实现恒压输出；类似的，文献［18］针对串/串补偿网络，利用原边电流产生同相的自激驱动信号，获得了与负载变化无关的恒流输出，但二者的输出增益均与耦合系数相关。为了适应变耦合工况，文献［18］在自激控制回路中引入分频控制，利用非接触反馈构成闭环，使得自激间歇工作，实现对输出电流的调节。为了实现变负载、变气隙、错位条件下输出基本恒定，文献［19］提出了另一种自激控制思路:检测串/串补偿拓扑副边电流的过零点，产生原边开关管的驱动信号，使得系统能自动追踪与负载和耦合系数均无关的固定增益频率。在此基础上，文献［20］将相位检测线圈与原边功率线圈进行了集成，提出了三线圈结构的自激式串/串补偿谐振变换器，以提高功率密度。但文献［19-20］所提的自激控制只能保证输出电压的基本稳定，其输出本质上还是开环控制。实际输出电压因负载变化、线路寄生电阻以及电流相位检测误差等原因，波动较大。

为此，本文针对三线圈结构串/串补偿自激控制系统，引入动态基准作为调节变量，以满足输出精确控制要求。首先，介绍了基于动态基准调节的自激控制概念，说明了输出电压调节机理，在此基础上，建立控制系统的开环传递函数模型，分析基准电压取值对自激工作频率与输出电压的影响，给出最大调控电压、基准电压等关键参数的设计依据。进一步，提出了检测便捷、延迟时间小的输出过/欠压状态信息反馈技术，并给出了自激式输出电压精确控制策略的具体实现方法。最后，设计并搭建了一台80 W实验样机证明了本文所提控制策略的有效性。

1 基于动态基准调节的自激控制策略

1.1 新型自激控制策略的提出

图1（a）给出了本文所提基于动态基准调节的自激式串/串补偿IPT系统的结构框图，其中:Vin、Vo分别为直流输入、输出电压；vgs为驱动电压，图中以0-1量表示；vAB为逆变器输出交流方波电压，图中以0-1量表示；L1、L2和L3分别为 原、副边功 率绕组与短路绕组的自感；M12、M13和M23为三绕组之间的互感，对 应的耦 合系数分别为k12、k13和k23；i1、i2和i3分别为 流过L1、L2和L3的 电流；C1、C2分别为 原、副边串联补偿电容；r1、r2和r3为回路寄生电阻；RL为负载电阻；v3为电流采样电路输出；Vcomp为动态基准电压。

图1 基于动态基准调节的自激控制策略Fig.1 Self-oscillating control strategy based on dynamic reference modulation

自激控制工作过程为:副边绕组电流i2经磁场耦合使得短路绕组流过同相位的电流i3，i3经电流、电压转换得到v3；将v3与动态基准电压Vcomp进行比较，经过波形处理后转换为占空比为0.5的方波，驱动逆变器的开关管，从而维持变换器的自激工作。相关波形如图1（b）所示。与现有的自激控制策略［19］相比，本文所提控制策略引入动态基准，提供了一个新的可调节变量Vcomp，在保留自激控制良好动态性能的同时，可实现对系统输出的精确调控。

定义引入动态基准后，vAB与i2之间的相移时间为tc，对应的转移阻抗角为θ。假设逆变器的工作周期为T，采样输出v3波形在过零点处的斜率为a，由图1（b）可推导得到Vcomp与tc、θ之间的函数关系为:

显然，动态调节Vcomp的数值，即可调控vAB与i2的相位差。

1.2 输出电压调节机理

对图1所示功率变换器采用基波近似分析方法，得到附录A图A1所示基波等效电路。基于变压器互感模型与基尔霍夫电压定律（KVL），可以求得变换器的输出电压增益Gv以及转移阻抗Z21［20］，具体表达式如下:

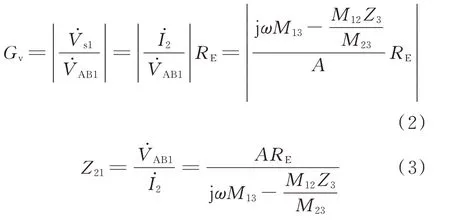
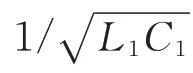
结合附录A图A2（a）不难看出，在ZVS频率区间内，转移阻抗角θ随工作频率单调变化，反之，调节θ，自激稳定振荡频率也会随之变化，而工作频率的改变又会影响输出电压增益，如图A2（b）所示。因此，通过引入动态基准，调节θ，控制自激工作频率，可实现对输出电压的调控。但需要注意的是，输出电压增益随工作频率的变化是非单调的，这使得Gv存在极大值点，限制了IPT系统可调输出电压的上限。另外，也限制了频率调节范围，只有设计调节频率在最右侧峰值点的右半部分，如图A2（b）中阴影部分所示，使得Gv随频率始终单调变化，才能实现输出的负反馈调节。

具体的电压调节过程如图2所示。在耦合机构与负载参数发生变化时，自激响应能够使得系统快速追踪到增益交点频率（ωH）附近，同时动态基准可实现对输出电压的负反馈调节:检测到输出电压升高（减小）时，控制动态基准电压Vcomp增大（减小），转移阻抗角增大（减小），以提高（降低）自激工作频率，减小（增大）输出电压，从而维持输出电压的稳定。

图2 基于动态基准调节的自激控制输出电压调节过程Fig.2 Output voltage regulation process of selfoscillating control based on dynamic reference modulation

2 关键参数设计依据

第1章介绍了基于动态基准调节的自激控制理论以及输出电压调节机理，在此基础上，本章建立控制系统的开环传递函数模型，分析基准电压取值对自激工作频率与输出电压的影响，由此给出最大调控电压、基准电压等关键参数的设计依据。

2.1 控制系统传递函数

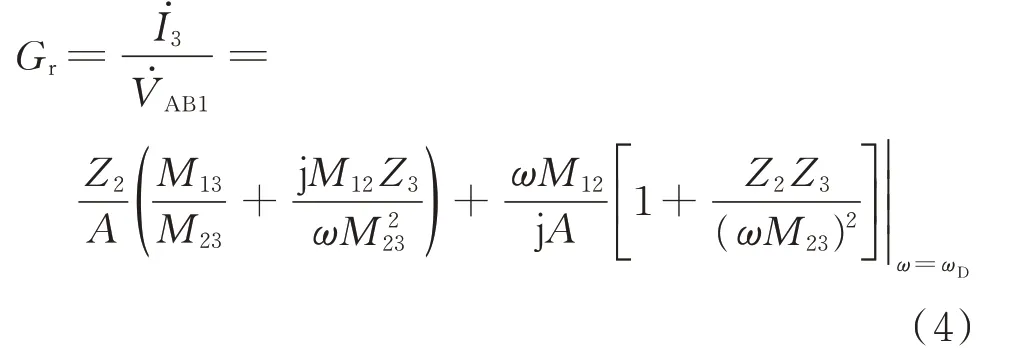
GCS为电流采样电路的传递函数，可等效成一个比例K0，GCS=K0。GPWM为驱动信号产生过程的传递函数，根据图1（b），可将其等效为一个相位超前调节环节:

式中:tx为等效相移时间，包括动态基准引入的可控相移时间tc和实际控制回路中存在的固有器件延时t0，tx=tc−t0。

GAC为驱动信号vgs到逆变桥输出电压vAB的传递函数，其表达式为:

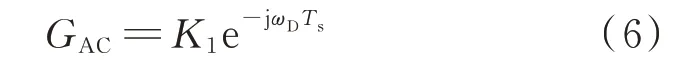
式中:K1为功率放大系数；Ts为开关器件延迟时间。

自激控制环路的传递函数Gid为:

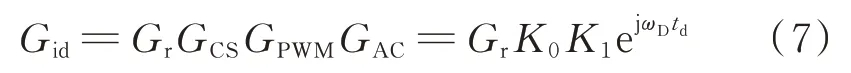
式中:td为vAB相对于短路绕组电流i3的总相移时间，td=tc−t0−Ts。由于传递函数Gid的输入、输出信号均为vAB，因此其虚、实部Im（Gid）、Re（Gid）满足Re(Gid)=1＞0且Im(Gid)=0。

令Im(Gid)=0，可以得到系统自激振荡频率ωD与相移时间td的隐式表达式F（ωD，td），忽略k13与寄生电阻，F（ωD，td）的表达式如式（8）所示。

进一步，结合Re(Gid)＞0可以解得实际的自激振荡频率ωD:

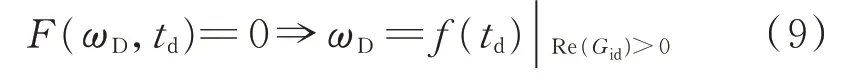
将ωD代入式（2），即可求得系统输出电压增益关于相移时间td的开环传输函数Gv，con为:

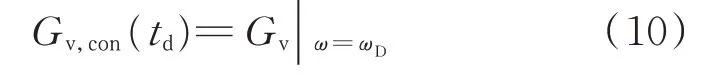
由式（1）可求得动态基准电压Vcomp与总相移时间td的关系式为:

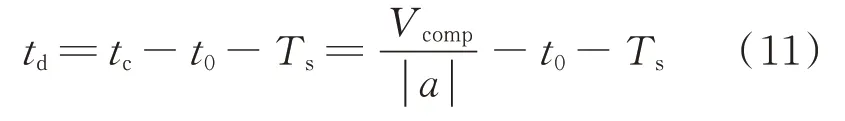
将式（11）代入式（8）、式（10），即可得到ωD、输出电压增益关于动态基准电压Vcomp的函数表达式。考虑到式（11）中a、t0、Ts均为可变量，参数不确定，为了减少分析的变量数，在下文的讨论中选用相移时间td来描述动态基准电压Vcomp的影响。

2.2 动态基准对工作频率与输出电压增益的影响

式（8）、式（10）的解析式不易得出，但可以应用Mathcad或MATLAB数学分析软件进行数值求解。代入附录A表A1中的参数，计算得到不同耦合系数与负载电阻下，系统自激振荡频率ωD与稳态输出电压增益Gv，con随相移时间td变化的曲线分别如附录A图A4（a）和（b）所示，其中td＞0表示vAB超前于i3，td＜0表示vAB滞后于i3。

可见，引入动态基准后，实际自激工作频率ωD会相对理想自激振荡频率ωHi（i=1，2，3，分别对应三档耦合系数）发生偏移，且随着相移时间td单调递增。那么，控制基准电压增大，也即增大td，提高工作频率，与图2中的控制逻辑相符。

附录A图A4（b）给出了系统输出电压增益Gv，con与td的函数曲线，显然，动态基准（相移时间td）对IPT系统的输出电压具有调节作用，但它也存在局限性:①输出电压不能任意调节，在每组（RE，k12）下，Gv，con均存在极大值点，故动态基准所能调控的最大输出电压是有界的；②相移时间参数不能随意选取，为保证输出负反馈，相移时间调节区间应设置在Gv，con单调变化区间。

2.3 输出电压限值

记Gv，con极 值 处 的 相 移 时 间 为tdp，增 益 极 值 为Gv，conp，则对于任意一组（RE，k12）参数，均存在一组（tdp，Gv，conp）与之对应，相应地，系统所能调控的输出电压范围为0～Gv，conp。为了在全部负载、耦合系数变化范围内均能实现恒定电压输出，所设计的IPT系统的额定输出电压Vo应不大于min{Gv，conp}，其中min{⋅}表示返回最小值。

令∂Gv，con/∂td=0，解得tdp，代入式（10）即可求得Gv，conp的函数曲线，如附录A图A5（a）所示，其中Q为线圈品质因数（Q=(ωDLi)/ri，i=1，2，3）。由图A5（a）可见，Gv，conp随负载电阻单调递增，随耦合系数单调递减，其最小值min{Gv，conp}在最大耦合系数、最小负载电阻处取得。因此，应设计额定输出电压Vo满足式（12）。

2.4 动态基准调节区间设计

假 设 可 控 相 移 时 间 范 围 为td，min～td，max。为 了 在全部参数变化范围内均能实现对输出电压的负反馈调节，应设计td，max≤min{tdp}或者td，min≥max{tdp}，其中max{⋅}分别表示返回最大值。

绘制不同k12下，tdp随负载变化的曲线，如附录A图A5（b）所示。由该图可以看到，在RE与k12变化范围内，tdp存在最大值，且发生在最小负载与最大耦合系数工况。令k12=1，RE=0Ω，求得此时tdp≈0，故max{tdp}始终小于等于0。那么设置td，min≥0，即使得vAB超前于短路绕组电流i3，就可以保证输出电压增益随相移时间单调变化。

3 自激式输出电压闭环控制电路设计

应用动态基准控制理论实现输出电压闭环调节，还需要输出电压反馈，因为需要依据输出电压动态调节比较Vcomp的数值。常规红外、蓝牙、Wi-Fi、Zigbee等无线通信方式握手时间较长、存在延迟，快速性不好，且输出电压反馈需要模数、数模转换等多个环节，实现复杂［11］。为此，本文提出了基于过/欠压状态信息反馈的非接触滞环调节器，依据输出过/欠压状态调节Vcomp，从而将输出模拟信号的非接触反馈需求转化为简单的数字电平信号反馈需求，实现简单，传输延迟小。图3给出了闭环控制电路的原理框图，包括信号反馈电路、电流相位检测电路、动态基准调节电路与驱动信号产生电路这4个部分，所有电路均由模拟电路搭建，具有良好的实时性。图3中:LPF表示低通滤波，BPF表示带通滤波。

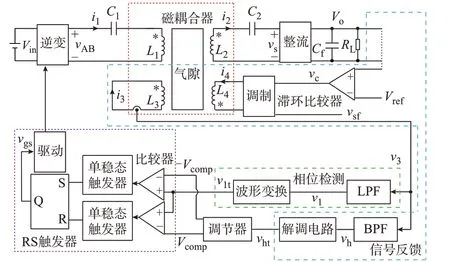
图3 自激式输出电压闭环控制电路原理框图Fig.3 Block diagram of self-oscillating closed-loop control circuit of output voltage

3.1 输出过/欠压状态信号反馈电路

如图3所示，信号传输采用磁耦合反馈方式，在耦合机构的副边增加绕组L4，用于数字信号发射，并复用短路绕组L3接收数字信号。数据传输过程为:采样直流输出电压Vo，并将其与输出基准电压Vref作滞环比较，输出表征输出过压、欠压状态的高、低电平，分别对应数字“1”和“0”；然后，利用载波振幅键控（amplitude shift keying，ASK）调制原理，将数据信号调制到高频载波上，通过松耦合绕组L4、L3实现无线传输；原边检测电路采样流过短路绕组L3的电流，并将携带数字信息的高频载波提取出来，再经过解调电路，从而将副边输出状态信息恢复出来。具体的电路实现及关键电压、电流波形如附录A图A6所示。为避免混淆，记功率传输频率为fd，高频载波频率为fe。

附录A图A6（a）中，L4、r4为信号发射绕组的自感、寄生电阻，Cf1为谐振电容，与L4在载波频率fe处谐振，Rf1为限流电阻。vsf是高频载波，vc为待传输的数字信号，vc控制与L4并联的双向开关S，对载波信号进行调制。如图A6（b）所示，vc为低电平时，S断开，vsc激励Cf1、Rf1、L4、r4串联谐振回路，在L4中流过高频谐振电流，vc为高电平时，S导通，将绕组L4短路，电流为零，故流过L4的电流i4被调制为:

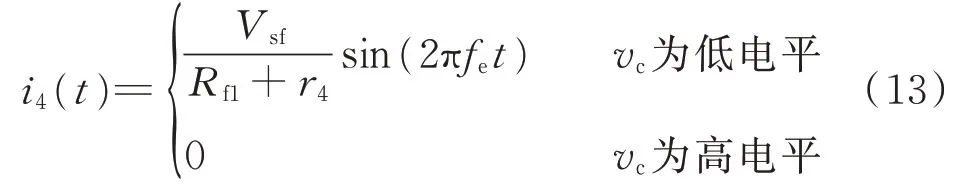
式中:Vsf为vsf的基波有效值。

由于共用磁场耦合通道，L3感应出同时包含能量和数据的信号，如附录A图A6（b）所示。原边信号接收电路中，高频带通滤波器用于提取携带副边状态信息的载波频率信号vh，包络检波器提取信号包络，低通滤波器滤除包络中的高频噪声，放大器用于放大低通滤波器输出信号的幅值，比较器用于判断传输信号的高、低电平，将输出电压的状态信息还原，完成数据通信。最终，比较器输出电压vht＞0，表示输出欠压；vht＜0，表示输出过压。

这里虽然能量传输与数据传输共用耦合机构，线圈间存在交叉耦合，但由于各自谐振网络的谐振频率差异，二者之间的相互干扰很弱。通常，为了保证信号的传输速率，往往设计载波频率为能量传输频率的10倍及以上，达到兆赫兹级［21］。设计Cf1与L4在载波频率fe处谐振，即等效构成一个带通滤波器，一方面可有效阻止能量信号进入数据传输回路，减小对数据传输的干扰；另一方面，谐振还可以减小数据回路的阻抗，增大数据信号的幅值，保证数据传输的有效性。反过来，功率回路谐振网络的选频放大作用也会使得耦合到能量回路中兆赫兹载波信号强度急剧衰减。因此，输出过/欠压状态信号反馈电路具有较强的抗干扰性。

3.2 自激式非接触滞环调节电路

附录A图A7（a）和（b）给出了电流相位检测电路与动态基准调节电路的原理图及相关的波形示意图。

忽略k13［20］，基于互感理论，求得短路电流为:

式中:k34为绕组L3和L4之间的耦合系数。可以看到，i3的能量信号与副边功率绕组电流i2同相。故滤除i3中的载波频率信号，即可获取副边能量接收线圈电流相位信息。

如附录A图A7（a）所示，电流相位检测电路采样短路绕组电流i3，经RC低通滤波，得到滞后于副边功率绕组电流i290°相位的正弦信号vl，并经运算放大器对vl的幅值进行放大。考虑到正弦波形的非线性，直接将其与动态基准电压Vcomp比较，难以建立Vcomp与相移时间tc间精确的函数关系，故本文采用过零比较器与积分电路将正弦波转换为三角波vlt，vlt峰值电压为:

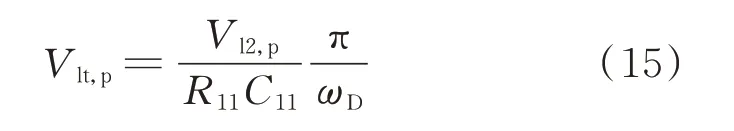
式中:Vl2，p为过零比较器输出电压vl2的峰值电压；R11和C11分别为调节比例-积分（PI）控制器的电阻和电容。由附录A图A7（b）可以看到，三角波vlt与副边功率绕组电流同相，实现了对副边功率绕组电流相位的检测。

动态基准调节电路根据反馈得到的输出电压过/欠压状态信息，通过积分调节器调节动态基准电压Vcomp。如附录A图A7所示，输出过压时，反馈低电平信号，Vcomp增大；输出欠压时，反馈高电平信号，Vcomp减小，与图2所示的控制逻辑相符。图A7（a）中限幅电路用来调整Vcomp的调节区间，反相器输出−Vcomp。

进一步，将电流相位检测信号vlt分别与动态基准调节电路的输出电压Vcomp、−Vcomp交截，可得到逆变器的驱动信号，电路实现如图3中的紫色虚线框所示，比较器输出经单稳态触发器后输出边沿信号，再用RS触发器还原成方波信号vgs。由附录A图A7（b）可以看到，引入动态基准后，驱动信号超前副边绕组电流的时间为tc，且随着Vcomp增大，相移时间tc增大，转移阻抗角增大，结合图2可知，相应的自激工作频率会提高，使得输出电压减小，进而实现对输出电压的负反馈调节。

需要注意的是，考虑到驱动信号vgs是由三角波vlt与Vcomp、−Vcomp交截得到，为了获得驱动信号，对三角波的幅值提出了要求，即

式中:|Vcomp|max、ωD，max分别为|Vcomp|、ωD所能取 得的最大值。

结合式（15）与式（11），可以求得相移时间td与动态基准电压Vcomp间的函数关系为:

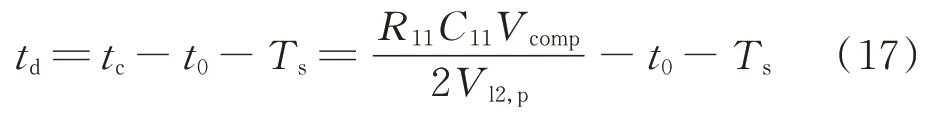
3.3 集成电流相位检测与输出反馈功能的耦合机构

附录A图A8给出了闭环控制所用耦合机构示意图，包括原、副边功率绕组L1、L2，短路绕组L3，以及副边数据发射绕组L4，其中L3与L1集成，共用原边磁芯，L4与L2集成，共用副边磁芯。功率传输绕组L1、L2采用双极型线圈绕制方式，左、右两侧磁力线方向相反；短路绕组L3包围整个原边绕组L1，通过调整其相对位置，可使得L3耦合到的L1中激励电流产生的进、出磁通相互抵消，两绕组间耦合系数k13为 零［20］。类 似 的，将L4包 围 整 个 副 边 绕 组L2绕制，实现副边侧两绕组之间的磁解耦。需要注意的是，实际使用中很难设计k13真正为零，如附录A表A2所示，但由于k13的存在仅会导致i3略超前于i2［20］，等效在控制环路中引入一个很小的超前时间环节，包含于td中，因此对本文的分析结果没有影响。

耦合机构中，L1、L2承担功率传输的功能；检测绕组L3短路，与副边功率绕组L2构成了非接触电流互感器，检测流过L2的电流相位；同时检测绕组L3与数据发射绕组L4耦合，用于实现输出电压状态信息非接触反馈。

4 实验验证

4.1 系统参数

为了验证上述自激闭环控制策略的有效性，本文采用附录A图A8所示耦合机构搭建串/串补偿非接触谐振变换器，实验装置如图A9所示。实验所用耦合机构参数与功率电路器件、关键元件参数如表A2、表A3所示。

由附录A表A2、表A3可确定耦合系数的变化范围为0.15～0.38，负载电阻的变化区间为8～25Ω，代入式（12）可以求得闭环调控的输出电压限值应为1.02Vin，其中输入电压Vin范围为28～33 V，故输出电压限值为1.02×28 V=28.56 V。表A2中系统额定输出电压26 V小于28.56 V，满足输出电压限值要求，因此，采用本文所提出的自激闭环控制策略可实现恒压输出。

4.2 数据反馈信道性能测试

为验证所设计信号反馈电路数据传输的可靠性和有效性，基于EP4CE6F17C8控制芯片调制生成高频载波信号与基带信号，对信号传输通道的延迟时间、信噪比、误码率进行测试。实验中，谐振变换器功率电路采用开环定频控制，工作频率为124 kHz，输入电压为30 V，负载电流为3 A，控制器周期性地发送信号序列0010111000，基带速率为50 kbit/s，载波频率为1 MHz，实验结果如附录A图A10所示。

附录A图A10（a）中，vc为待传输的数字信号，i4为调制后流过L4的激励电流，vh为原边提取出来的高频载波信号，vht为最终解调出来的数字信号。可以看到，解调vht信号与传送信号vc互反，与图A6（a）中给出的理论结果相符，验证了信号传输方案的有效性；最终解调出来的数字信号与初始发送的数字信号上升沿存在1.76μs的延迟，下降沿存在1.44μs的延迟，较小的延迟时间使得副边输出电压状态信息可以快速地被原边接收，响应快。

用示波器读取接收信号vh的数值信息，导入MATLAB数学分析软件，采用snr函数可以绘制得到接收信号的频谱，如附录A图A10（b）所示，并计算得到传输信道的信噪比（signal-to-noise ratio，SNR）。图A10（b）结果显示，满功率输出时信道的信噪比为15.96 dB，因此数据能够可靠传输。控制器EP4CE6F17C8检测解调出来的数据信号并与发射信号进行判决，分析传输信道的误码率，如图A10（c）所示，误码率小于0.1%。

4.3 控制系统性能测试实验结果

首先，确定动态基准电压的调节范围Vmin～Vmax，由3.4节的分析可知，为保证对输出的负反馈调节，可调相移时间的最小值应大于等于0，代入式（17）可求得Vmin≥[(t0+Ts)2Vl2，p]/(R11C11)=−0.27 V。将附录A表A2、表A3所示的电路参数代入式（10），计算得到闭环控制的输出电压增益Gv，con随动态基准电压Vcomp的变化曲线，如图A11所示，为满足表A3中所需增益调节范围0.76～0.93，Vmax设为0.6 V。此外，由图A11可以看到，在Vcomp调节区间内，输出电压增益Gv，con随Vcomp单调变化，Vcomp越大，Gv，con越小。

附录A图A12给出了过/欠压状态下电流相位检测电路中电压、电流的实验波形，图中各变量参数定义同图A6，可以看到2种输出电压状态下，输出三角波vlt均能跟随副边功率绕组电流i2的相位，实现相位检测，但由于寄生电阻与器件延迟，vlt相对i2存在约220 ns的超前，故取t0=−220 ns。

附 录A图A13为气隙间 距g分别取1、2、3 cm情况下Vcomp、Vo和vc的稳态波形，可以看到，输出电压始终控制在滞环范围内，输出欠压时，vc为低电平，控制Vcomp线性减小，使得Vo增大；过压时，vc为高电平，控制Vcomp线性增大，使得Vo减小，由此实现了对输出电压的负反馈调节。气隙间距g分别取1、2、3 cm情况下，Vcomp平均值分别为0.26、0.18、0.27 V。图A13中，Vin=30 V，RL=15Ω，则Gv=0.86。由图A11可以计算出气隙间距g分别取1、2、3 cm情况下输出闭环所需的理论Vcomp分别为0.23、0.18、0.24 V，与实验值吻合较好，验证了理论分析的正确性。将Vcomp的波形展开，得到不同Vcomp值下的驱动波形，如图A14所示。在Vcomp增大过程中，驱动电压vgs超前于副边功率绕组电流i2的时间增大，自激振荡频率增大，与图A4中的理论分析相符。

图4（a）和（b）为负载切换时的动态实验波形，由该图可见，输出电流Io从1 A跳变到3 A过程中，Vcomp由0.25 V跃变至0.05 V，输出电压经过0.8 ms左右的响应时间后进入稳态，稳定后的输出电压仍被控制在滞环范围内；Io反向跃变过程中，Vcomp由0.25 V跃变至0.05 V，从跃变起至输出稳定的时间也为0.8 ms左右。而目前常用的无线通信模块，如射频通信模块，系统动态响应时间均在10～100 ms数量级［11-12］，因此本文所提控制策略对负载扰动及突变具有较好的抑制能力和快速的动态响应能力。图4（c）和（d）为输入电压Vin切换时的动态波形，从图中可以看出，控制变量Vcomp始终动态跟随Vin变化，在整个Vin变化过程中控制输出电压一直保持稳定。输入电压Vin从28 V上升到33 V，相应的Vcomp从0 V增大到0.35 V，与附录A图A11中给出的理论计算结果相符。

图4 动态实验波形(g=2 cm)Fig.4 Dynamic experimental waveforms(g=2 cm)

实验还测试了不同气隙间距下，闭环控制时输出电压随负载电流变化的曲线，如图5所示。为了便于比较，图5中还给出了传统基于过零基准比较自激控制的负载调整率曲线（即令Vcomp=0 V）。可以看到，无输出电压状态信息反馈时，谐振变换器在变耦合系数与负载下虽然也能实现近似恒压输出，但存在较大的输出波动，输出电压在全参数变化范围内的波动为9.6%；相比之下，本文所提基于动态基准调节的自激闭环控制策略的输出波动要小得多，输出电压在全参数变化范围内的波动仅为2%，保证了输出电压精度，实验结果证明了本文所提控制策略的优越性。

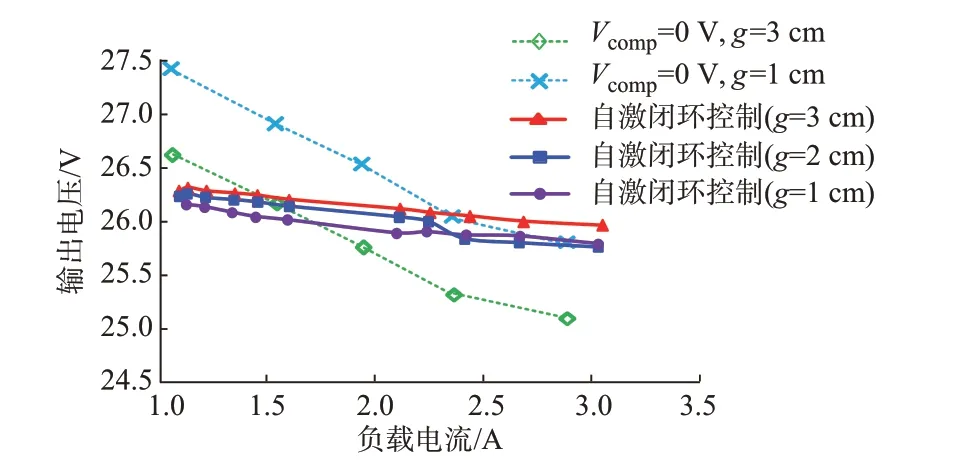
图5 不同气隙间距下输出电压随负载电流变化的曲线(Vin=30 V)Fig.5 Curves of output voltage varied with load current and different air gaps(Vin=30 V)

5 结语

本文提出了一种新型的自激控制策略，通过引入动态基准比较，在保留自激控制良好动态性能的同时实现了对系统输出的精确调控；建立了控制环路的传递函数，分析了动态基准对自激工作频率与输出电压的影响，给出了调控的单调区间与可调输出电压限值；提出了具有输出精确调节功能的非接触滞环调节控制方案，该方法仅需反馈表征输出过/欠压状态的高、低电平数字信号，检测便捷、延迟时间小，易于实现。本文还搭建了一台80 W的样机进行了实验，结果表明:数据传输的时延在2μs内，信噪比为15.96 dB，误码率小于0.1%，验证了数据传输的快速性与可靠性；在负载与耦合系数变化工况下，输出电压均稳定在滞环范围内，输出电流从3 A跳变到1 A时，系统动态响应时间约为0.8 ms，证明了所提控制策略具有较好的动静态性能。

为进一步提升动态响应速度，后续将研究采用更高频的载波调制方案，并结合手机充电等消费电子产品，采用所提控制策略开发相应的控制芯片。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。