师范生计算思维发展现状与影响因素——基于津冀鲁三地高校的调查

房 敏 孙 颖 陈 伟 吕慎敏

(1.天津大学 教育学院，天津 300350；2.曲阜师范大学 教育学院，山东济宁 273100)

一、研究背景

人工智能时代需要计算思维教育。计算思维(computational thinking)最早由卡内基·梅隆大学周以真(Wing，2006)给出定义，历经十余年发展，逐渐被视为一种适应信息化社会生存和发展的重要素质。统计显示，全世界已有52个国家明确将计算思维纳入小学课程(Tang et al.，2020a)，大量围绕计算思维教育的实验项目覆盖基础教育和高等教育，形式与内容呈现出多元与泛化的特点。随着人们对计算思维认识的深入，计算思维教育从单纯依靠信息技术专门课程走向跨学科融合教育，越来越多地关注普遍情境下复杂问题的计算化解决，国内外学者先后使用“计算思维2.0”(陈国良，2020)、“计算参与”(Yasmin，2016)等词汇描绘这一趋势。近两年来，我国教育部先后发文，明确将编程教学与实验教学、多学科教学融合，大力培养能够开展计算思维教育的中小学师资，这标志着K-12阶段的计算思维教育已不仅是信息技术教师的工作，也成为各类学科教师应承担的重任。

教育者计算思维能力水平直接影响计算思维教育质量，然而当前对学科教师及师范生计算思维的发展与评价研究较薄弱。从国际层面看，学者指出这一领域的实证研究偏少，多以质性研究为主，量化研究存在样本数少、信效度不足等问题(Kong et al.，2020；Tang et al.，2020b)。回顾国内研究进展可以发现，针对教师及师范生的计算思维探讨更少，已有研究多聚焦于国际计算思维教育标准引介及对教育者角色责任的思辨讨论，同样缺少针对计算思维教育者能力水平和发展特点的实证研究。鉴于此，本研究以未来的计算思维教育者——师范生为对象，从计算思维评价入手，探析我国师范生计算思维的特点及影响因素，为后续研究提供支持。

二、评价框架与研究问题

(一)评价框架

1.计算思维的认识取向：两种差异的分析与选择

研究者对计算思维组成成分的认识存在差异。近年来，有研究将合作、批判、创造力等非智力因素融入抽象、算法、模式识别等传统的计算思维智力要素。作为计算思维的核心成分(Filiz et al.，2016；Korkmaz et al.，2017；Akyol，2019)，本研究将非智力因素参与计算思维成分组成的认识差异称为第一种差异。师范生计算思维的界定采用何种取向，里昂等(Lyon & Magana，2020)指出，计算思维操作性定义需要与具体的教学活动和评价设计相结合才能产生实际意义。给出一个让师范生能够与自身学科知识和生活经验发生联系，还能嵌入学科教学活动实现职业化理解的定义，对于开展计算思维评价和提高研究信效度具有重要价值。因此，对这种差异选择的关键考量是，哪种取向能够清晰地向师范生解答跨学科计算思维教育的作用。一些研究者认为，非智力要素的引入有助于研究者和非计算机专业的教育者们跨学科地迁移解读计算思维，不仅能使计算思维贴近其他学科知识，也有助于塑造学习者的完整人格(Oluk & Korkmaz，2016；房敏等，2021)。本研究更倾向于非智力因素参与的认识取向。

基于是否需要思考计算思维的职业情境，又产生了第二种认识差异：一类观点从生活应用情境出发，将计算思维视为生存所需的基本能力，在培养与评价上与非师范类学生无差别。科尔克马兹等(Korkmaz et al.，2017)从跨学科角度提出的师范生计算思维评价体系，费尔哈特等(Ferhat & Pinar，2019)从计算机学科角度开展的师范生计算思维训练研究，均属这一类。另一类观点考虑了职业情境，把计算思维教学能力看作师范生计算思维的重要组成部分。阿科约尔(Akyol，2019)在分析已有计算思维量表时指出，应当在具体行业情境及职业生涯中探讨计算思维的成分和评价维度。一些研究者通过开展师范生训练活动、开发计算思维量表等方式，将这类观点付诸实践(Mouza et al.，2017；Peter et al.，2020)。鉴于计算思维教育能帮助师范生掌握计算机化思考的能力，理解这种思维与所学专业知识之间的联系，并在未来职业活动中有效传播计算思维，第二类观点已成为当前把握师范生计算思维内涵的主流取向。

2.计算思维的界定与评价框架构建

基于以上分析，本研究形成了对计算思维解读的两个基本观点：1)师范生计算思维不仅包括计算思维的一般应用能力，还包括相应的职业应用能力即教学能力，后者由前者发展而来；2)对不同学科师范生计算思维基本要素的理解，包括建立信息模型、运用算法方法、引入非智力要素和解决模型问题。本研究借鉴科尔克马兹(2017)对计算思维的表述，并结合教师职业特点认为，师范生计算思维是在一定情境下借助合作形式，运用算法方法创造性地解决问题，并能对这一过程进行绩效改进、策略泛化和有效传播的能力。在此基础上，本文参照国际主流师范生计算思维评价设计思路，结合房敏等(2021)面向我国师范生计算思维评价维度，构建了师范生计算思维评价框架(见图1)。

图1 师范生计算思维评价框架

(二)研究问题

1.计算思维发展的现状与特点

研究发现，非计算机专业的教师普遍对计算科学知识和计算思维有恐惧感，缺乏技术使用意识和计算思维教学信心，在计算思维概念理解和教学方法选择上也存在困难(Menekse，2015；Bower et al.，2017；Sands et al.，2018；Wang et al.，2020)。实验表明，绝大多数师范生能够经过培训快速掌握计算思维的相关概念和知识，但缺乏计算思维教学兴趣，也很难保持这种兴趣(Heintz et al.，2017；Zha et al.，2019)。通过分析可以看出，与生活密切相关的计算思维被师范生借助原有的信息技术知识同化发展后，能够与自身学科知识产生联系，形成可用于计算思维教学案例，但与计算思维教学相关的其他要素，如教学方法、策略、兴趣、态度等能力的提升不那么简单。然而，现有的研究结论几乎全部来自欧美地区，国内关于师范生计算思维水平的实证研究或经验性描述一直未见著述。因此，探析国内师范生计算思维的现状与特点，对于完善计算思维教育体系具有参考价值。

2.人口学因素对师范生计算思维的影响

区域和性别差异是目前探讨较多的两个造成计算思维差异的人口学变量。在区域研究方面，凯尔等(Kale et al.，2018)发现，美国南部三州城镇教师与乡村教师在计算思维知识、技能与教学能力方面差异显著。约瑟(Jose，2020)发布的发展中国家计算思维教育调查报告显示，经济状况良好的地区开展计算思维教育条件更成熟，计算思维水平也更高。在性别方面，罗曼等(Roman et al.，2016)调查显示，男性计算思维水平显著高于女性。亚达夫等(Yadav et al.，2014)发现，性别仅影响计算思维兴趣，而对计算思维其他成分的影响并不显著。埃维克等(Evik & Ata，2020)对师范生的调查发现，计算思维的各项能力在性别变量上均无显著差异。性别对计算思维的影响并未形成统一的结论，但最新的针对中国社会的人口学调查研究显示，性别对教育的获得产生显著影响(吴洁等，2020)。

基于以上分析，本研究提出假设1：城乡差异、区域经济差异和性别差异会对师范生计算思维产生显著影响。

3.学科专业对师范生计算思维的影响

不同学科背景的教师对计算思维认识不同，且存在能力差别(Jukeviien，2020；Angeli & Giannakos，2020)。在计算思维研究中，研究者达成了共识：按学科类别选择研究对象或课程科学合理也更具针对性。里昂等(2020)在系统回顾师范生计算思维研究文献的基础上，提出将师范生分为理工学科和以教育学科、人文学科为主的“非专业”学科(与信息技术专业相关度较低)分类探讨。宾等(Bean et al.，2015)将艺术类(音乐、美术等)师范生单独归类，与语言类师范生的计算思维进行对比。借鉴已有分类经验，本研究也将师范生分为理工学科、人文学科、教育学科、艺术学科四类。

基于以上分析，本研究提出假设2：学科专业会对师范生计算思维产生显著影响。

4.信息技术学习对师范生计算思维的影响

计算思维源于编程教育活动。房敏等(2020)通过元分析法发现，学习编程的学段和累计学习编程的时长对计算思维培养影响显著。奎尔斯等(Qualls & Sherrell，2010)认为，培养计算思维的信息技术课程应在小学开设，并持续到中学及以后。孙立会等(2020)借助皮亚杰(Piaget & Cook，1955)认知发展理论，论证了在中小学开展计算思维教育的重要性。近年来，越来越多的研究者开始关注小学低年级和学前阶段的计算思维教育，认为计算思维应提早培养(Herrero，2020；Saxena et al.，2020)。从国内信息技术教育体系看，多数省份已于小学三年级开设信息技术课程，部分地区自小学高年级(4-6年级)开始开设，还有部分地区虽然开设了此类课程，但往往开而不上(赵健等，2019)。而与信息技术、计算思维紧密相关的自然科学课程、游戏活动和课外培训项目，受教育竞争意识及欧美发达国家科学教育低龄化趋势影响(姚建欣等，2017)，又存在提前教育的现象。由此看出，一方面国内师范生的信息技术学习经历不完全一致，另一方面不同信息技术学习经历对计算思维产生的效果可能也不同。

基于以上分析，本研究提出假设3：开始学习信息技术的时间和累计学习信息技术的时间会对师范生计算思维产生显著影响。

5.教育技术课程对师范生计算思维的影响

教育技术课程是面向教师职业能力塑造、按照严格的职业能力培养顺序嵌入师范教育体系的公共课程，也是培养师范生计算思维职业应用能力最合适的途径(Yadav et al.，2017)。近年来，国际教育技术组织和学者以教育技术课程为依托开展了系列计算思维教育研究。罗梅罗等(Romero et al.，2017)借助教育技术课程面向基础教育专业师范生实施计算思维教育，提出了计算思维评价改进方法。金等(Kim et al.，2012)通过使用Scratch、学习机器人等工具变革教育技术课程教学方法，提升未来教师适应和发展的能力，同时提出教育技术课程应重点关注包含计算思维在内的思维技能培养。埃维克(2020)认为，教育技术课程可以加深师范生对媒体技术的认识，更容易采用并设计整合计算思维的教学案例。由此推断，教育技术课程不仅可以直接或间接地向师范生提供计算思维知识、技能和观念；更重要的、也是区别于信息技术课程的是，它将师范生的计算思维延伸到教育职业领域，并提供迁移经验和训练机会。

基于以上分析，本研究提出假设4：教育技术课程会对师范生计算思维产生显著影响。

三、研究设计

(一)研究对象

本次调查时间为2020年6月至2021年1月，采取目的抽样、分层抽样和随机抽样相结合的方式，确保样本代表性和对无关变量的控制。调查以全日制本科在读师范生为对象，师范生身份认定标准为：1)所属专业的人才培养方案明确以在各级各类学校和教育机构从事教育工作为主要就业目标；2)人才培养内容包含教育学、教育心理学、教学法课程和教育实习(或以教育单位为依托的毕业实习)。选取地理区位靠拢、文化习惯相近、经济水平有一定差距(以人均GDP衡量，数据来自国家统计局)的天津、河北、山东三地作为样本抽取的省级行政单位，并至少选择一所综合性院校和一所师范院校展开调研。出于对人口规模、高等师范教育规模和免费师范生教育政策的考虑，抽样对象侧重山东地区，最终选取八所高校，其中天津市二所(天津大学、天津师范大学)，河北省二所(河北大学、衡水学院)，山东省四所(山东师范大学、济南大学、山东女子学院、济宁学院)。专业覆盖语文、数学、外语、物理、化学、政治、历史、信息技术等基础教育常见课程，并按学科专业分为理工、文史、教育、艺术四大类(分类标准下文详述)，年级覆盖大一至大四(以调研时间点计算)。调查抽样确保每个省级行政区内涵盖上述四大类，且每个大类的样本至少包含两个及以上的年级(绝大多数为三到四个年级)，被调查者年龄介于16-24岁。班级与学生以随机选取和自愿参与为主，问卷采用现场和网络发放相结合，最终回收问卷3358份，其中有效问卷3105份，有效率92.47%，被调查者基本情况见表一。

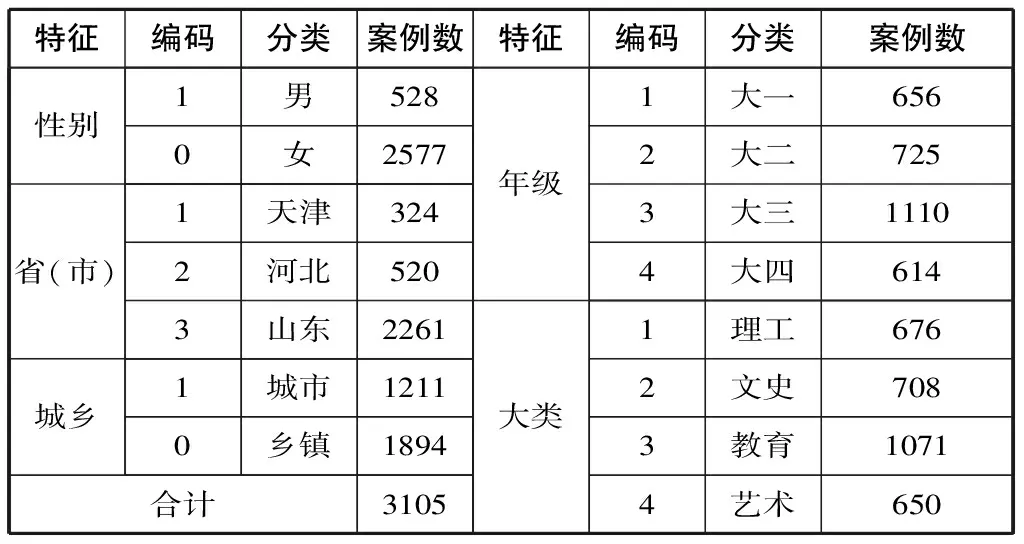
表一 调查对象基本信息

(二)分类设计

本研究对学科专业、学习学段等进行了分类与编码。其中，学科专业按上文提出的四大类划分，分类标准参考《普通高等学校本科专业目录(2020年版)》、被调研高校相关专业授予学位类别和已有研究的分类经验，学科专业与大类划分对应关系见表二，具体编码工作由调查对象自行勾选修读专业后，再由研究人员对照关系表实施。学习计算机/信息技术相关课程的学段设计，按照小学1-3年级、4-5/6年级、初中、高中、大一(计算机公共课程)、大二/大三(教育技术课程)进行分类，采用复选方式供被调查对象选择，未勾选项赋值0，勾选的选项赋值1，选项赋值加和用于衡量正式教育中的信息技术知识累计学习时间，括号内课程代表当年修习了该课程，未修习则不勾选。将计算机公共课和教育技术课作为单独学段赋值计算基于以下考虑：一是两者知识体系相对独立且完整，分置于不同学年且有先后修习关系；二是两者知识内容丰富，每门课程的授课学时和内容量基本达到基础教育阶段二年左右的信息技术课程教育当量；三是方便对教育技术课程修习效果进行检验。

表二 学科专业-大类划分对应关系

(三)研究工具

本研究使用房敏等(2021)开发的师范生计算思维量表作为评价工具，包括导语和题目两部分：导语为师范生计算思维的定义，辅以简单解释，确保调查对象阅读后能够理解计算思维概念。题目共32题，均采用李克特五级量表，涵盖问题界定与分析(PDA)、问题认知与解决(PCS)、教学策略与实施(ISI)、教学兴趣与设计(IID)、创造力(CA)五个维度(对应图1)。在原研究中，量表总体信度和各维度信度为：αCT=0.955，αPDA=0.910、αPCS=0.897、αISI=0.884、αIID=0.866、αCA=0.766。本研究的量表总体信度和各维度信度为：αCT=0.943，αPDA=0.908、αPCS=0.825、αISI=0.861、αIID=0.873、αCA=0.724。在使用Amos进行模型拟合度检验时，由于样本数量大(n>3000)，χ2值受样本数量影响较大(Kline，2011)，因此本研究仅提供χ2/df结果数值，不设参考值，其他各项指标均在理想范围(见表三)，表明该量表推广使用具备良好的信效度。本研究采用主观汇报填写，需要共同方法偏差检验，经Harman单因素方法检验，第一主成分因子方差解释率为37.059%，小于临界值40%，经潜在误差变量控制法检验，ΔRMSEA小于0.05，其他各指标差值小于0.1(见表三)，可见本研究共同方法偏差不明显。

表三 模型拟合度及共同方法偏差检验

四、结果与分析

(一)正态性检验与总体分析

本研究使用SPSS24分析处理数据，借助P-P图和Q-Q图正态分析各维度及总体得分发现，数据基本呈正态分布；偏度、峰度正态性检验显示，各维度和总体得分偏度介于-0.206与-0.018之间，峰度介于3.338与3.902之间，满足正态分布判断条件，但各维度和总体得分呈微弱的负偏态、尖峰分布趋势，表明师范生计算思维自我评价具有轻微趋同性和偏积极认知。各维度和总体得分的描述性统计发现，师范生在问题认知与解决、创造力维度的评价最高(分别为M=3.524，SD=0.553和M=3.524，SD=0.554)，其次为教学策略与实施(ISI，M=3.413，SD=0.448)，问题界定与分析、教学兴趣与设计维度的评价得分相近且较低(分别为M=3.316，SD=0.679和M=3.313，SD=0.701)。由此看出，师范生在计算思维应用(问题解决、教学实施等)的得分较高，概念、算法、表征等计算思维知识内容和计算思维教学兴趣态度得分较低，一定程度上反映了师范生对计算思维认识不足，兴趣匮乏，由此可以初步判断我国师范生与国际研究描述的师范生计算思维特点相似。

(二)影响因素分析

1.人口学变量的影响

对省市、城乡和性别变量的单因素方差检验发现，部分分组数据存在方差不齐，故采用Welch方法检验判断，使用Scheffe方法对方差齐性分组进行事后检验，使用Games-Howell方法对方差不齐分组进行事后检验，结果见表四。本研究对三个省级行政区的政治、文化、经济分析发现，三省(市)地域毗连，互为高考生源地，教育政策、文化习惯相近，结合全国2005-2019年(此阶段基本覆盖调查对象接受学校教育的时间)人均GDP经济面板数据来看，三地存在较大的经济差异。从数据结果看，省域间的区域经济差异未对师范生计算思维发展水平带来显著影响(pCT=0.365)。从城乡视角看，来自城市的师范生计算思维发展水平显著高于来自乡镇的师范生(pCT=0.000，η2p=0.023)。从性别看，性别变量对教学兴趣与设计维度影响显著(pIID=0.000)，但效应较弱(η2p=0.008)，在其他维度和总体得分差异不显著。

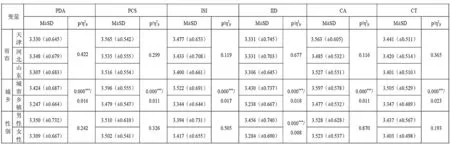
表四 省市、城乡、性别变量对计算思维的影响

2.学科专业的影响

对学科专业大类分组进行单因素方差分析结果见表五。数据表明，除问题认知与解决维度外，计算思维其他维度和总体水平均在大类分组上呈显著差异。在问题界定与分析维度，理工类显著高于其他三类(分别为pPDA=0.025，0.006，0.008)；在教学策略与实施维度，文史类显著高于教育、艺术类(分别为pISI=0.017，0.021)；在教学兴趣与设计维度，理工、教育类显著高于文史、艺术类(分别为理工类pIID=0.000，0.000和教育类pIID=0.035，0.039)；在创造力维度，理工类显著高于教育类(pCA=0.006)。总体而言，理工类显著高于教育、艺术类(分别为pCT=0.019，0.006)。由此看出，不同学科专业的师范生，计算思维水平存在差别，学科专业确实对计算思维产生了显著影响，但结合效应值判断，影响并不大。

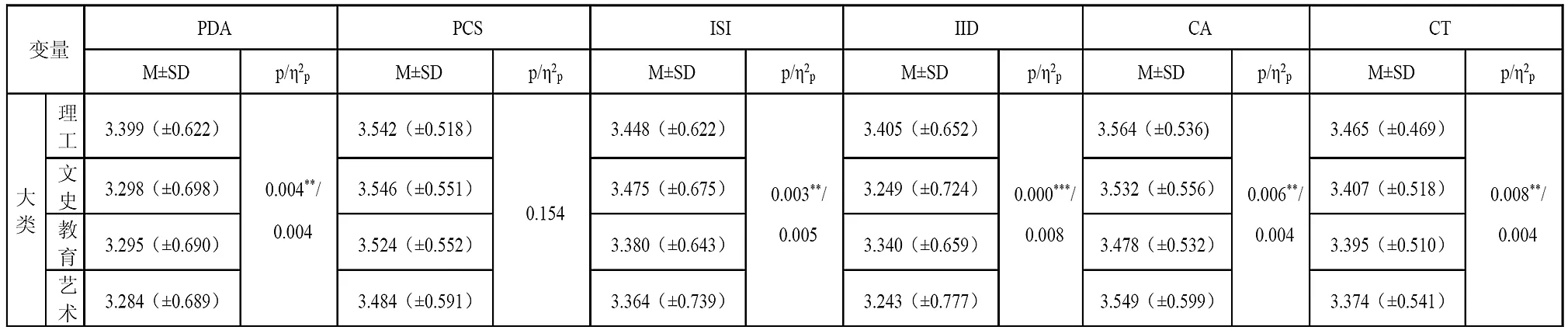
表五 学科专业对计算思维的影响

3.信息技术学习经历的影响

本研究设计了最早学习信息技术的时段(Et)和累计学习信息技术的时段(St)两个变量探析信息技术学习经历对计算思维的影响。依据教育政策和实践经验推断，两个变量存在相关和交互关系。经斯皮尔曼相关性检验发现，两变量显著相关且达到中度相关性(p=0.000，r=0.700)。采用多变量两因素方差分析检验的结果见表六，可以看出，最早学习信息技术的时段和累计学习信息技术的时段对计算思维总体水平影响显著(pCT=0.000)，且二者对计算思维的影响存在交互作用，但交互效应较弱(η2p=0.009)。经主效应和简单效应事后检验发现，累计学习信息技术的时段对计算思维水平影响较大，学习时段越长，计算思维水平越高。最早学习信息技术时段的影响较复杂，事后检验结果见表七。总体看，小学和初中阶段开始学习信息技术对计算思维的培养效果显著优于高中后，且开始学习的学段越低，效果越明显；问题界定与分析、问题认知与解决维度的检验结果与总体水平表现基本一致，小学低年级阶段开始学习信息技术的作用效果更明显；因教学策略与实施维度在最早学习信息技术的时段分组上的效应检验不显著，故不进行事后分析，而教学兴趣与设计维度仅在高中阶段出现，明显低于其他阶段的特异性，可以判断教学策略与实施、教学兴趣与设计两个维度受最早学习信息技术的时段变量影响较小；在创造力维度，小学阶段开始学习效果显著。交互检验轮廓图(见图2)清晰显示，从小学至初中阶段，学习阶段越早，学习时间越久，计算思维水平越高；高中及以后学习信息技术，短期时间提升计算思维的效果并不明显；计算思维教学能力受信息技术起始学习时间影响较小。

表六 信息技术学习经历对计算思维的影响

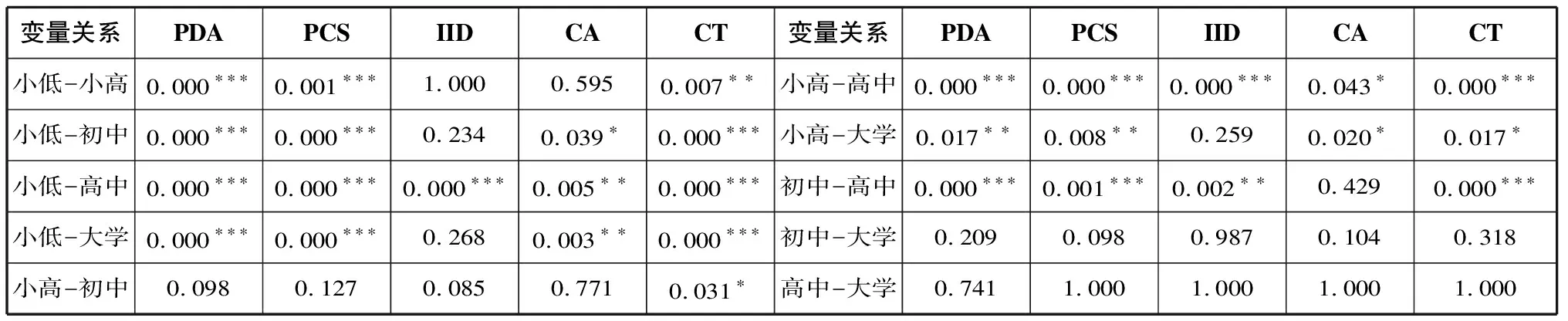
表七 最早学习信息技术时段对计算思维影响的事后检验

图2 交互检验轮廓图

4.教育技术课程对计算思维的影响

师范生培养方案将教育技术课程定位于促进师范生信息化教学能力的发展，那么教育技术课程对计算思维培养是否发挥了作用，是否对所有专业的师范生都发挥了作用？为了回答这些问题，本研究采用多变量两因素方差分析，探讨教育技术课程对不同类别师范生计算思维发展的影响，结果见表八。由此看出，教育技术课程的主效应及与学科大类的交互效应均对计算思维各维度产生显著作用(p<0.01)，特别是在教学兴趣与设计维度上(η2p>0.02)。这说明教育技术课程确实对不同学科产生了不同作用，差异作用的事后检验结果见表九。由此看出，教育技术课程对文史类师范生的计算思维各维度影响不显著(p>0.05)，对教育、艺术类师范生的计算思维各维度影响显著(p<0.01)，对理工类师范生计算思维的问题界定与分析、教学策略与实施和教学兴趣与设计维度影响显著(分别为p=0.001，0.007，0.000)，而在问题认知与解决、创造力维度并无显著影响(p>0.05)。

表八 教育技术课程对计算思维的影响

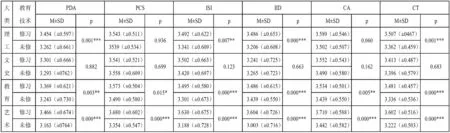
表九 不同类别师范生学习教育技术对计算思维影响的事后检验

五、讨论与总结

(一)研究讨论

本研究反映了国内师范生计算思维发展水平的现状和特点，揭示了影响师范生计算思维发展的部分因素，以及计算思维教育体系存在的问题。本部分将数据统计结果、访谈时发现的线索与推断存在的问题结合起来讨论，以更好地呈现研究价值。

1.分裂与异化：计算思维发展不均衡与对“快餐化”教育的质疑

通过分析数据，本研究发现师范生计算思维能力发展不均衡，在面向实际问题的操作能力自我评价上更积极，而在计算思维概念、知识、方法，以及在教育情境应用计算思维信心不足。研究者尝试借助不同教学方法通过短期训练提高师范生的计算思维知识水平和教学效能(Adler，2017；Piedade，2020)，然而政府的跟踪调查项目质疑了这类训练的长效性(Heintz，2017)，特别是对知识熟练度、教学兴趣和意愿的保持作用。从图2看，虽然累计学习信息技术的时段对计算思维作用显著，但低累计学习时段对计算思维的提升作用并不明显，这反映了计算思维并非速成能力。此外，分析图2的小学折线走势可以发现，低累计学习学段向高累计学习学段过渡期间相应的计算思维水平增长明显，斜率较大，说明计算思维教育出现学段断层会对计算思维发展产生明显的不利影响，尤其是在兴趣培养和概念形成方面，造成了后续教育技术的授课困境。

根据问卷调查数据和已有研究判断(赵健等，2019)，中学学段信息技术教育缺失是造成低累计学段值的主要原因。在功利的办学向标下，信息技术教育价值的人为弱化割裂了学生信息技术能力发展的完整性，造成了计算思维能力体系中科学与人文品质的非和谐统一。美国计算思维数字徽章项目正尝试在学校教育体系外，通过提供完整的开放教育资源，支持学生和教育者完整而持续地发展，并期望通过混合认证的方式激励学习者的学习动机(Hunsaker & West，2019)。我国具有适宜的组织优势进行类似尝试，但与正式教育体系相关课程关系还需深入探讨和厘清。总体来讲，师范生的计算思维培养需要科学系统、完整持久的发展体系，一是对于优秀的短期项目，宜围绕教育对象的能力短板进行改造与吸收，纳入国内师范生计算思维的培养体系和课程方案；二是加强基础教育阶段信息技术课程师资建设，落实信息技术课程质量保障监督机制；三是改变单纯依靠学校，或以学校为主商业机构为辅的教育局面，推动开放教育系统及地方电教部门合作建立标准统一、形式多元的计算思维教育及认证体系。

2.性别与经济：社会环境对单一因素决定论的反证与解释

通过对性别变量的检验，本研究发现性别对计算思维影响较小，仅对教学兴趣与设计维度影响显著。对K-12阶段学生计算思维性别差异的追溯可以更好地解释这一结论。埃斯皮诺等(Espino & González，2015)发现，幼儿阶段儿童计算思维同质性明显，当前多数研究认为小学阶段男女生的计算思维兴趣存在差异但不显著，且这种差异在不同研究中各有高低(Master et al.，2017；Sun et al.，2021)，而进入更高学段后，性别维度产生了显著的兴趣预测作用(Yadav et al.，2014)，本研究也发现了这一点。社会视角研究认为，儿童自学前段就开始接受了具有性别差异的职业引导(Fulcher，2008)，男性在接受技术教育过程中得到了更多的支持和鼓励(吴洁等，2020；Sun et al.，2021)，潜移默化地影响了女性的技术兴趣和参与意愿。由此看出，社会的分工需要与环境要素的刻板暗示，导致了性别维度的计算思维兴趣差异。因此，在基础教育阶段保持女童计算思维的兴趣，尤为重要。

通过对省市和城乡变量的检验，本研究发现存在一定经济差距但教育政策、文化习惯具有相当同质性的省份之间计算思维差异并不明显，而在省域内部的城乡变量上差异较大。出于对人口学变量交互作用的考虑，本研究再次进行了协变量控制的多元线性回归分析，得到了相同的显著性检验结果，进一步证实省域间无差异，仅有城乡变量存在显著区别，这一结论否定了经济差异会造成师范生计算思维发展差异的观点。很多研究认为经济是影响教育水平的核心要素，并通过财政分配影响教育政策实施(Jose，2020；王善迈等，2013)。而近年的教育研究显示，经济要素的影响在减弱，教育政策、社会文化及人口结构等社会因素的影响在不断提升(李颖等，2015)。当经济水平达到一定高度后，基础教育所需财政支持不会造成沉重的负担，因此与教育密切相关的其他因素表现出更强的作用。本研究选取的省份虽存在较大的经济差异，但均在平均水平之上，就很好地说明了这一点。针对城乡变量的研究发现，来自乡镇的师范生普遍接受信息技术教育较晚，学习“断档”现象严重，且教师信息化教学能力显著弱于城市(孙妍妍等，2021)，这些都解释了师范生计算思维为何在城乡变量上差异明显(η2p>0.02)，也证明了综合社会环境因素在师范生计算思维发展上起重要作用。

3.生活与职业：计算思维发展关键期及早期教育价值的探讨

通过对信息技术学习经历变量的检验，本研究发现最早学习时间和累计学习时间对师范生计算思维产生显著而独特的影响。从一般能力看，研究者普遍认为5-6岁和10-11岁是发展数理思维的关键阶段(Piaget，1955；刘晓明等，1999；Hermans & Aivaloglou，2017)，后一个年龄段基本对应我国小学3-6年级(按6或7周岁入学)。结合本研究结果分析，小学阶段开始学习信息技术的效果明显优于其他学段，特别是小学低年级开始接触信息技术知识效果更突出，反映了小学低年级阶段更可能是儿童计算思维发展的关键期。对于具体在几年级开始进行计算思维教育活动最合适，研究者并未形成一致的观点。部分国外实证研究表明，小学2-3年级开设信息技术课程最合适，还有部分研究者认为，对计算思维的有意识培养应以游戏化的形式提前至学前阶段的中大班(Denner et al.，2019)。然而，国内研究表明，儿童计算认知能力在小学1-3年级阶段发展迅速，但个体差异远大于年级差异(龚少英等，2004)，本研究采纳了这一观点，从儿童认知发展差异和教育公平的角度出发，未对小学低学段再做细化，也不期望提出更具体的时间节点，将探索和设计的空间留给地方教育部门和学校更合适。

从职业能力看，根巴特(Guenbatar，2019)发现师范生进入职业领域后运用计算思维解决问题的能力成长变缓甚至停滞，而其他与教育活动密切相关的计算思维能力会继续得到发展。与之相似，本研究揭示的作为专门培养计算思维教育应用能力的教育技术课程，在问题界定、分析、解决等维度产生的作用明显弱于对教育应用能力培养的作用。此外，通过对大四(经历教育实习，修习了教育技术课程)与大二、大三(未经历教育实习，修习了教育技术课程)的单因素方差分析也发现，他们之间问题解决能力差异并不明显(大四-大三：pPCS=0.191，大四-大二：pPCS=0.064)，而计算思维教育应用能力有显著提升(pISI=0.000，pIID=0.000)，说明教育实习环节同样更多地在职业能力发展上产生作用。不可忽视的是，教育技术课程和教育实习环节同样提供了发展计算思维一般能力的机会，但这些努力并未产生期望的效果。以上数据为计算思维不同子能力存在发展关键期提供了佐证，同时也说明计算思维教育体系的设计应在不同阶段重点关注不同能力的培养，在基础教育阶段重点发展计算思维生活应用能力，在高等教育中后段侧重发展职业应用能力。

4.现实与超越：教育技术课程价值的失落与变革

通过对教育技术学习经历在不同学科专业的作用效果检验，本研究发现教育技术课程对教育、艺术类师范生的计算思维提高作用显著，对理工类师范生的问题认知与解决和创造力、文史类师范生全部维度作用微弱。脱离自身学科专业知识，理工、教育、艺术类师范生都能够在课程体系中找到与专业发展相关的技术内容(如计算机技术、多媒体技术等)，而文史类专业师范生由于知识贯通点较少，技术兴趣和创新冒险意识较弱(见表五)，很难产生知识共鸣。有研究者指出，现有的教育技术课程往往专注于教学技术工具的讲解演示，未能与学科知识和其他教育课程的教学法知识融合(Yadav et al.，2017)，也未能有效建立TPACK-CT的能力关联(Shinas et al.，2015)。国内调查也反映了我国教师上课时往往更关注于信息技术应用，而非思维能力的培养(郭芳等，2008)，教育技术发力点的错位引发了“教育技术危机”的讨论(吴刚，2020)。

为更好地发挥教育技术课程的作用，一些致力于嵌入式计算思维教育的学者开展了融合教育课程改革的尝试，将计算思维作为方法而非技术嵌入不同教育技术学习模块中，让学生设计最基本的学科教学案例，集中进行大量的教学展示(Mouza et al.，2017)。这种“低标准、宽口径、高强度”的课程设计形式有助于学生发展计算思维与自身学科之间的联系，形成实践性知识。此外，将可视化编程工具(如Scratch)作为课程独立模块，帮助构建基本的计算思维概念和激发学习兴趣(Lehtinen et al., 2016)，对于非理工类师范生是可以尝试的选择，但这类学习工具不适合连续或长时间在课程教学中应用(Kim et al., 2012；Mouza et al.，2017；房敏等，2020)。可以预见，未来教育技术课程将进一步走向技术分化和知识泛化，更灵活地适应技术进步对未来教师提出的能力诉求(Manches et al.，2020)，然而其面向的核心素质不会发生改变。面对大班制混专业授课困境，加强教育技术教师思维而非技术教学的意识和能力，打造面向不同学科师范生的经典计算思维教学案例，提供更多训练和展示的机会，是基于现实条件的可行选择。

(二)研究总结

本研究来源于对计算思维教育价值的反思和完善计算思维教育体系的现实需要，在“学科教育+”计算思维的背景下，结合当前师范生计算思维发展路径和研究结论，抽取关键要素深入探讨师范生计算思维发展的外部动因，论证国际研究普遍关注的若干作用变量的本土实证意义。所以放弃分步多元线性回归分析，一是诸多研究已论证了部分变量作用的独立性，即使有交互作用的变量也可采用协变量控制、主效应和交互效应分析进行探索；二是本研究分类变量较多，多元回归反而不利于展示和论述变量的作用机制；三是对多元回归的事后检验与探讨，依然要回到方差分析的技术层面。为进一步证明效度水平，本研究再次实施了对以上七个变量的分步多元线性回归分析，在显著水平上得出了与方差分析一致的结果。

本研究认为，师范生计算思维发展存在不均衡的特点，社会环境的综合作用、信息技术教育体系的科学完整性以及教育技术课程的形式内容都对其产生了作用。对人口学变量的检验结果否定了社会上存在的“性别决定论”“经济决定论”观点。作为高阶复合能力的计算思维，从单一的内、外生变量做出决定性论断显然是不科学的。对信息技术和教育技术学习经历的检验结果认同了计算思维是一种可培养的素质，计算思维不同子能力的发展存在不同的关键期，当前研究更多地关注了计算思维一般能力发展的黄金时期，而对职业能力发展选择了思辨讨论或直接忽视。从这一角度看，致力于发展计算思维职业应用能力的教育技术课程应当被赋予更丰富的内涵。对教育技术课程在各学科类别的检验结果反映了其现实价值的缺陷，教学条件的制约与技术的飞速发展为教育技术课程带来了实践层面的严峻考验，面向不同专业的教育活动，降低准入基线与提高技术水平产生矛盾点，化解的关键在于围绕思维教学目标校准课程靶向和提升课程精度，课改的路径亦应在科学化的价值审视和检验中不断得到论证、调整和发展。