多点激励简支梁桥车桥耦合振动响应
韩智强, 李路遥, 周勇军, 李华腾, 刘世忠, 晋民杰
(1.太原科技大学交通与物流学院,太原 030024; 2.长安大学公路大型结构安全教育部工程研究中心, 西安 710064)
随着国民经济飞速发展,交通状况日趋复杂,车辆与桥梁相互影响较为突出[1]。古典车桥耦合振动分析通常将车辆简化为集中力、简谐力或质量块等,桥梁被简化为有限梁单元进行求解。针对车桥耦合方法的求解,中外学者提出匀速移动常力、匀速移动简谐力、匀速滚动质量、匀速弹簧-质量等相关计算模型,使得车桥耦合仿真计算成为可能。随着计算机技术快速发展,实现车桥耦合精细化分析成为可能。李江龙等[2]基于车辆动力响应功率谱密度,采用自编软件,对桥梁安全性进行评价分析;Shen等[3]基于模型缩聚理论,采用模态分析和车桥耦合瞬态分析,实现多自由度车桥耦合仿真分析;肖乾等[4]分析胎压变化对车桥系统的振动影响,得出胎压变化对系统横向动力响应和走行滑移量有一定影响。赵越等[5]基于等参映射及改进折半法建立车桥耦合分析系统,建立多种精细化车辆模型,并通过全过程迭代法求解车桥耦合系统,其收敛速度较快;许汉铮等[6]采用17自由度三轴空间车型,分析横竖向车桥耦合曲线桥的动力响应,结果表明:曲线桥梁前两阶以竖向振动为主,且横竖向车桥耦合在曲线桥梁动力分析中较为重要;在多车车桥耦合方面,相关学者也开展了相关研究;王娟等[7]采用多个集中弹簧-阻尼-质量系统作用于简支梁桥时,随着各个敏感参数变化,桥梁动态响应变化;经薇等[8]建立多车激励简支梁桥车桥耦合分析模型,采用频域和时域进行数值分析,并根据边界条件验证了方法的正确性。
上述研究成果主要集中于单车车辆分析或者多车等效集中弹簧-阻尼-质量系统,分析桥梁振动特性,对桥梁冲击系数的研究相对较少。因此,基于车辆动力学的相关原理,理论推导多车车辆动力学方程,采用模态综合法建立多车车桥耦合分析系统,并与相关文献算例结果进行对比分析,验证方法的正确性,并考虑在一定车辆间距和数量下桥梁的动力响应变化,计算其冲击系数,并与多国规范值[9]进行比较,相关研究成果可为公路桥梁多车车桥耦合分析和冲击系数的计算提供指导。
1 基于模态综合法的多车车桥耦合分析系统
1.1 基本假定
(1)车辆在桥面行驶的过程中车轮时刻紧贴与桥面不发生分离。
(2)忽略桥梁横截面的变形。
(3)桥梁采用瑞雷阻尼,即桥梁阻尼矩阵与质量矩阵和刚度矩阵呈线性相关[10]。
1.2 车辆动力学方程的建立
以多辆两轴车为对象,根据车辆的动力特性,将其简化为4自由度的平面车型,包括车体的沉浮和点头,前后车轮浮沉。两轴车简化模型如图1所示,图1中:miv和Jiv为第i辆车车体质量和点头转动惯量;mix1和mix2为第i辆车前后悬架和轮对质量之和;cis1、cis2和kis1、kis2为第i辆车前后悬架弹簧阻尼系数和刚度系数;cit1、cit2和kit1、kit2为第i辆车前后车轮的阻尼系数和刚度系数;ziv和θiv代表第i辆车车体浮沉位移和点头角位移;yd和wj分别代表车轮位移和车轮与桥面接触点处的桥面竖向位移。

L1和L2为两轴车辆前后悬架至车辆形心间纵向距离,m; Zvr为车体竖向位移,mm; yi1为第i辆前悬架竖向位移,mm; yi2为第i辆后悬架竖向位移,mm;ZCl1为第i辆前轮对竖向位移,mm; ZCl2为第i辆后轮对竖向位
根据D’Alembert原理建立多车动力学运动方程[11],如式(1)所示:

(1)

分别对车体、悬架和轮对的4自由度进行受力分析,根据公式(1)建立n辆车车体动力平衡方程,整理成矩阵形式,如式(2)所示:
(2)
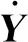
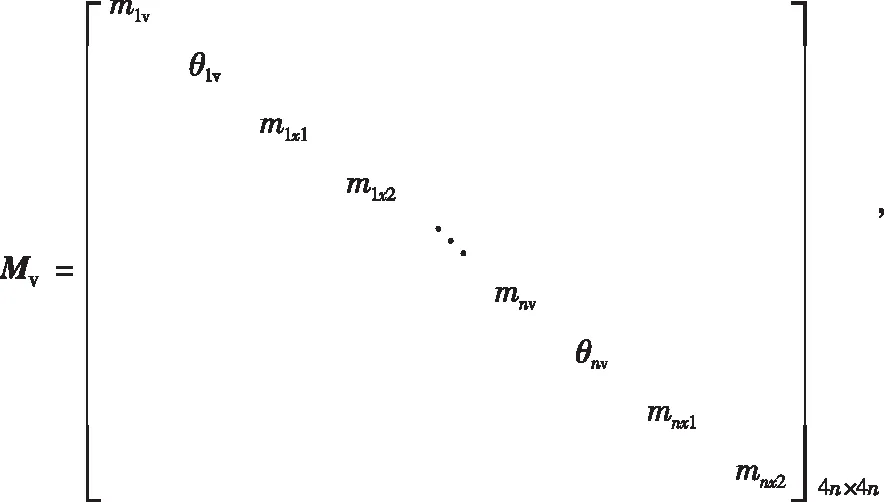


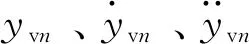
1.3 桥梁动力方程的建立
通过有限元软件建立桥梁仿真模型,通过模态分析获取桥梁的固有角频率ωj和振型向量Φ,采用振型叠加法构造桥梁模态方程,并将结构物理坐标转换为模态坐标,如式(3)[12]所示:
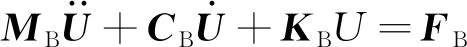
(3)
式(3)中:MB=ΦTMΦ为桥梁结构正则化模态质量矩阵;其中M为桥梁结构质量矩阵;CB=ΦTCΦ为桥梁结构正则化模态阻尼矩阵,其中C为桥梁结构阻尼矩阵;KB=ΦTKΦ为桥梁结构正则化模态刚度矩阵;FB=ΦTF为桥梁结构模态力向量,其中F为车辆作用桥梁的荷载向量:

同理可得出CB和KB矩阵:
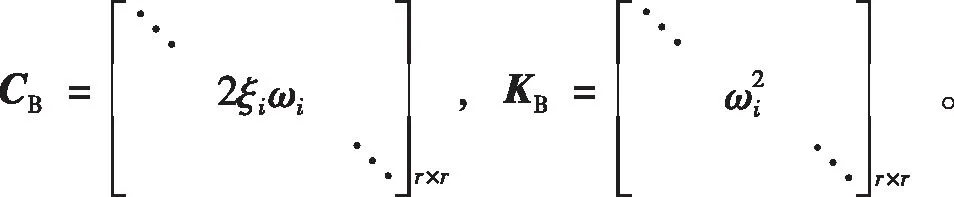
式中:ωi为桥梁第i阶自振圆频率;ξi为桥梁第i阶频率对应的阻尼比。
1.4 车桥耦合相互作用分析
如图2所示,假设车辆在桥面行驶过程中车轮时刻紧贴与桥面不发生分离,那么j点处车轮下缘的竖向位移为ydj。

图2 轮-桥接触点位移协调关系
ydj=wj+rj
(4)
式(4)中:rj为桥面不平整度,mm; 其他类同。
车轮下缘的竖向速度为
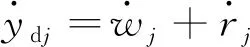
(5)
因此,车轮弹簧的压缩量和黏滞阻尼器的相对速度为
Δyj=yj-ydj=yj-(wj+rj)
(6)
(7)
式中:yj为车轮的浮沉位移,mm。
在求解j点处车桥系统的位移后,可推导车辆与桥梁在j点处的相互作用力fvbj,如式(8)所示。
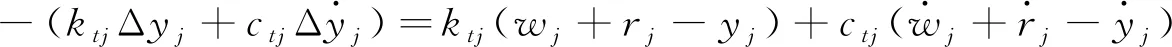
(8)
(9)
式中:ktj为车轮的刚度系数;ctj为车轮的阻尼系数;v为车辆行车速度。
将式(1)~式(9)进行整理,得出多车激励车桥耦合系统振动方程[13]为
(10)
式(10)中:MB为桥梁质量矩阵;CB为桥梁阻尼矩阵;CvB为桥车阻尼耦合矩阵;KB为桥梁刚度矩阵;KvB为桥车刚度耦合矩阵;FB为桥梁所受外力矩阵。
2 冲击系数计算方法
车辆荷载通过桥梁时,由于激振力作用桥梁产生的动力响应,形成冲击效应[9],为简化计算,采用冲击系数进行分析,冲击系数计算示意图如图3所示,计算公式如式(11)所示:

图3 车辆激励下桥梁跨中截面冲击系数计算示意图
μ=1-Ydmax/Yjmax
(11)
式(11)中:Ydmax为车辆过桥时,桥梁跨中截面动挠度的最大值;Yjmax为桥梁跨中截面的静挠度最大值。
2.2 各国冲击系数计算方法
(1)美国桥梁设计规范(AASHTO LRFD—2018)。桥面接缝-所有极限状态:μ=0.75;所有构件疲劳锻炼破坏:μ=0.15;其他状态:μ=0.33。
(2)加拿大桥梁设计规范 (DHBDC2006)。规范中冲击系数与汽车的轮轴数有关:当车辆轴数为1时,μ=0.4;当车辆轴数为2时,μ=0.3;当车辆轴数大于等于3时,μ=0.25。
(3)英国桥梁设计规范(BSI2006)中规定不同交通荷载冲击系数取值0.25。
(4)德国(DIN1072)规定。
μ=0.4-0.008L
(12)
式(12)中:L为桥梁跨径,m。
(5)中国公路桥涵通用规范[9](JTG D60—2015)。冲击系数与结构基频f的函数表达式为

(13)
式(13)中:f为桥梁结构的基频,Hz。
3 仿真验证
为验证本文方法的正确性,通过自编程序对参考文献[14]算例进行计算分析,相关参数如表1、表2所示,计算结果如图4~图6所示,由于篇幅有限,仅列举部分对比数据、对比结果。

表1 车辆技术参数

表2 桥梁技术参数
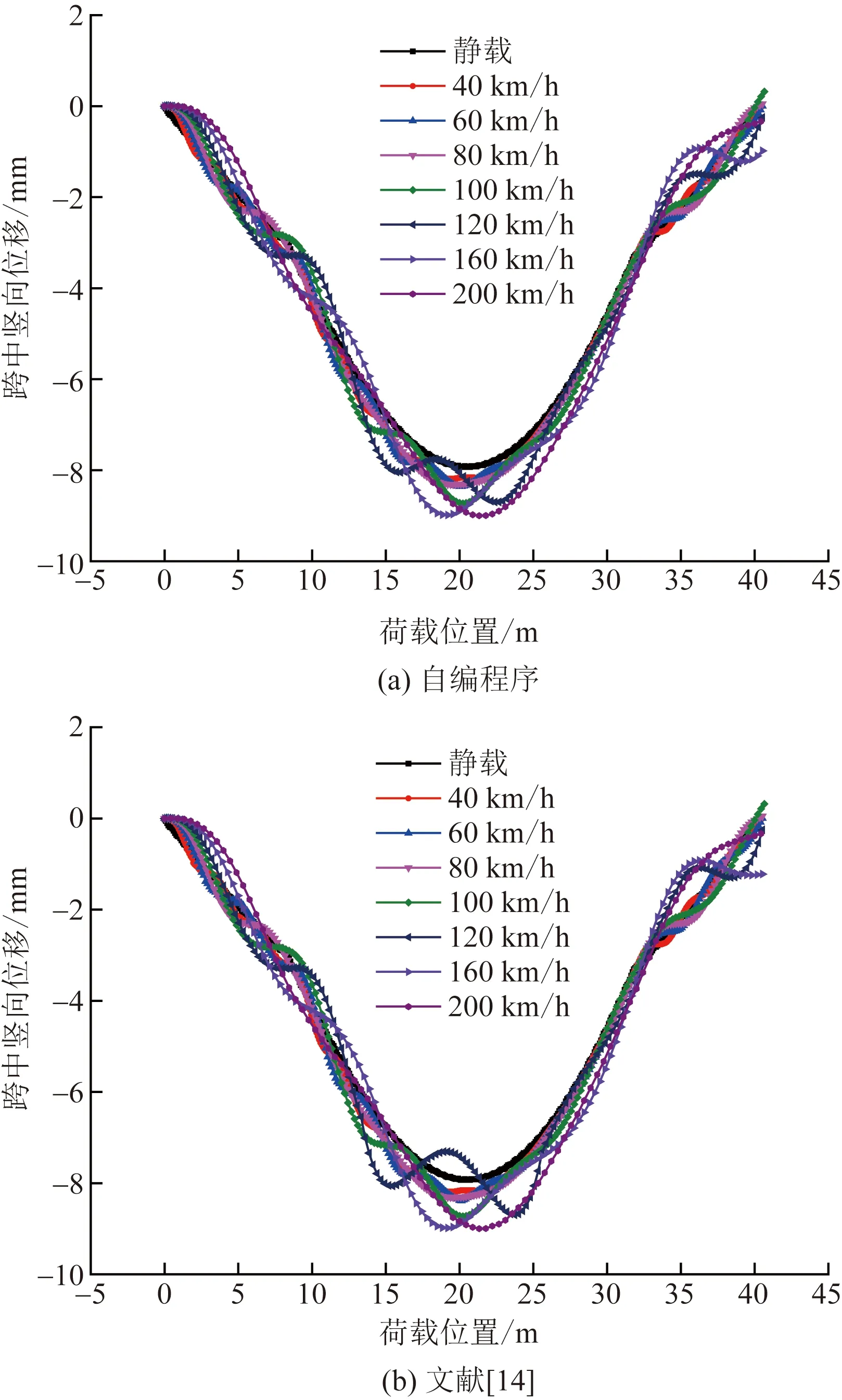
图4 32 m简支梁不同速度荷载作用下跨中位移时程曲线
如图4~图6所示,各个截面在不同车速下位移响应结果与文献[14]的计算结果较为接近,其曲线走势也较为吻合,不同行车速度下自编程序计算结果与文献[14]结果的相对误差均小于6%,验证了方法的正确性和适用性。

图5 速度v=40 km/h 的位移响应
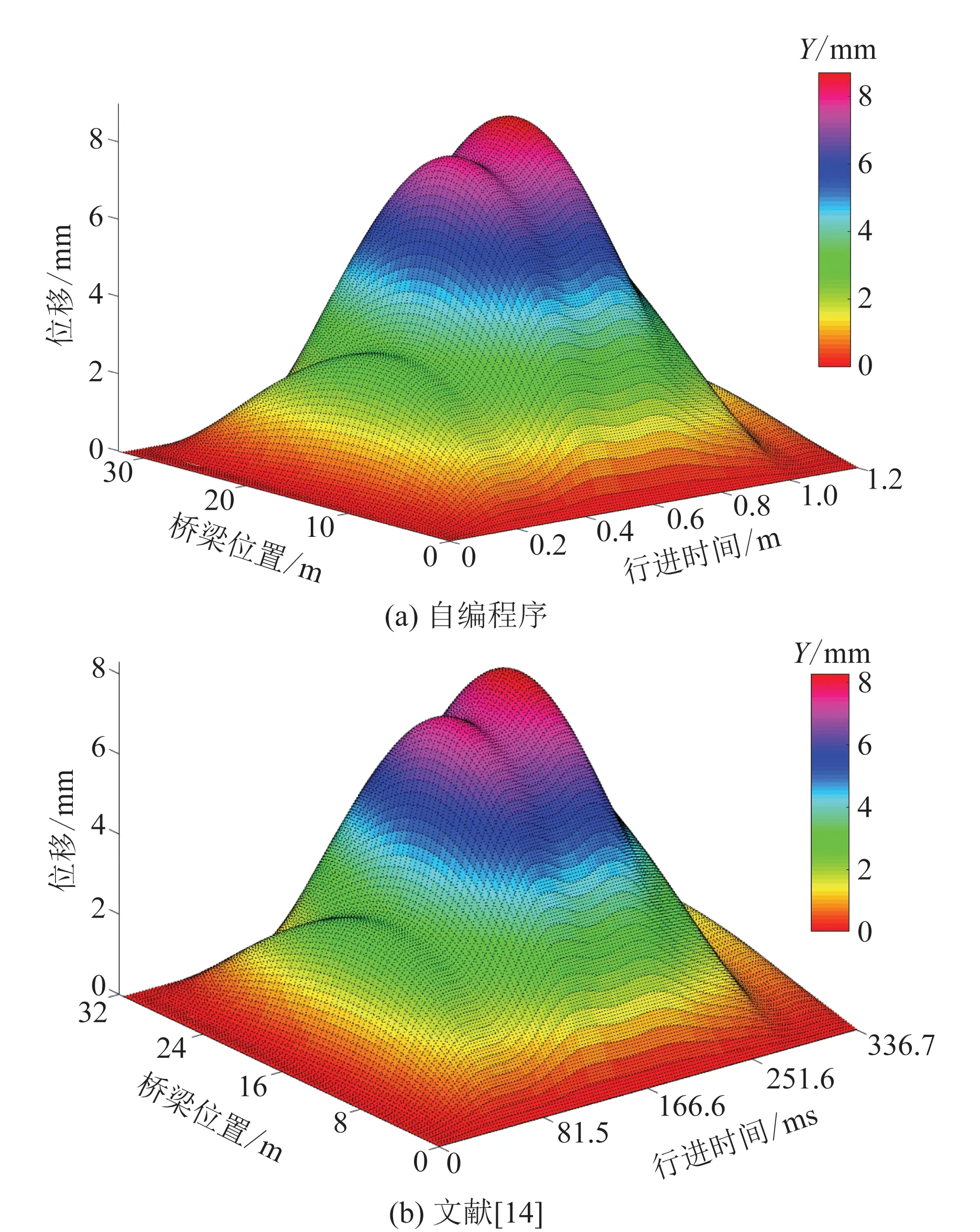
图6 速度v=120 km/h 的位移响应
4 多车车桥耦合振动研究
单辆激励通过桥梁时,结构动力响应能够一定程度上反映桥梁振动规律,但与实际情况有较大不同,为考虑纵向多车激励,车辆以车队形式通过桥梁时,其车桥相互作用更为真实,因此,开展多车车桥耦合振动分析及冲击系数研究有一定现实意义。
在多车车桥耦合分析时,车辆间距的不同,桥梁振动响应也不尽相同。为了充分了解不同间距对桥梁动力响应,定义车辆间距比p,如图7和式(14)所示。
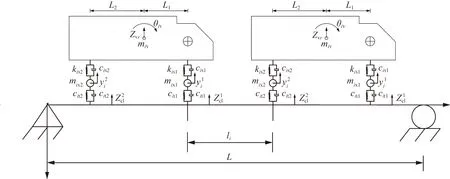
图7 纵向多车激励车桥耦合分析示意图
(14)
式(14)中:p为车辆间距比;li为相邻两车车辆间距,m;L为桥梁跨径,m。
4.1 不同车辆间距比下桥梁位移响应分析
为得到不同车辆间距比下桥梁的结构响应,对两辆车行驶通过简支梁进行仿真分析,其中桥面不平整度采用B级,通过自编程序建立了不同车辆间距比模型,并进行车桥耦合仿真计算,如表3和图8、图9所示。
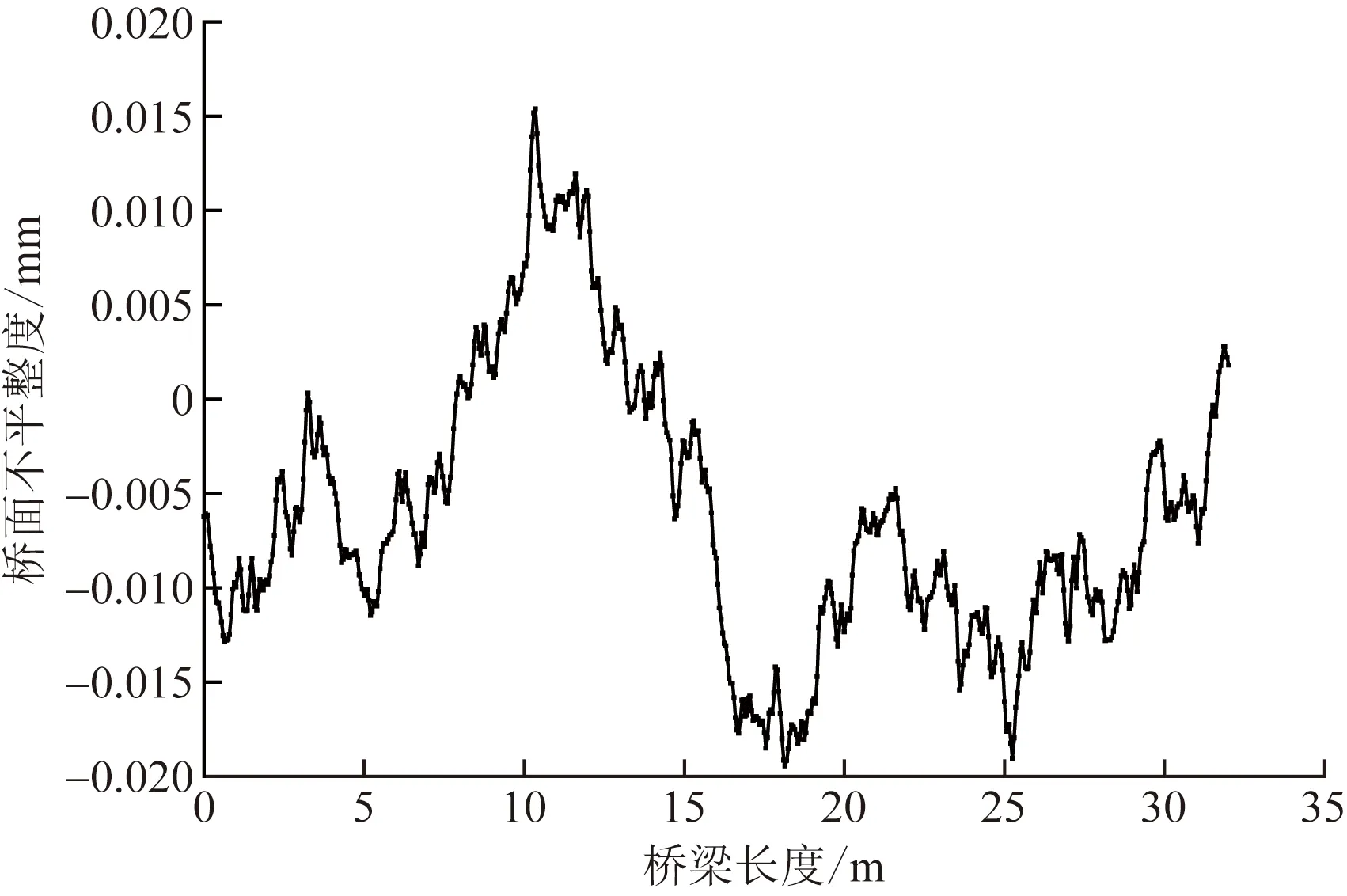
图8 B级桥面不平整度
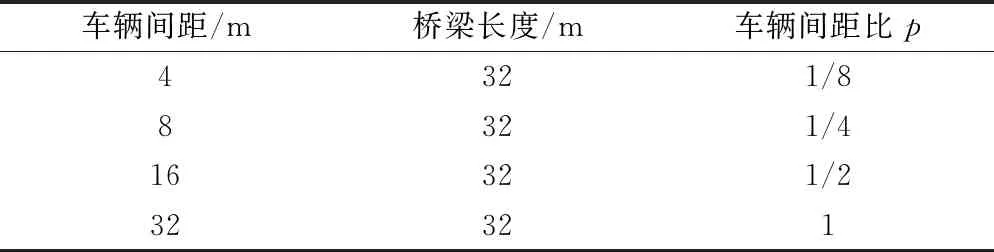
表3 不同车辆间距比
从图9可知,当两辆车辆以不同车辆间距比在桥上行驶,从上桥到下桥,桥梁跨中位移也不尽相同。随着车辆间距比p减小,桥梁跨中最大竖向位移呈增加趋势,当p=1/8和p=1/4时最大竖向位移明显增加,当p=1时,最大竖向位移接近单车时的桥梁位移响应。
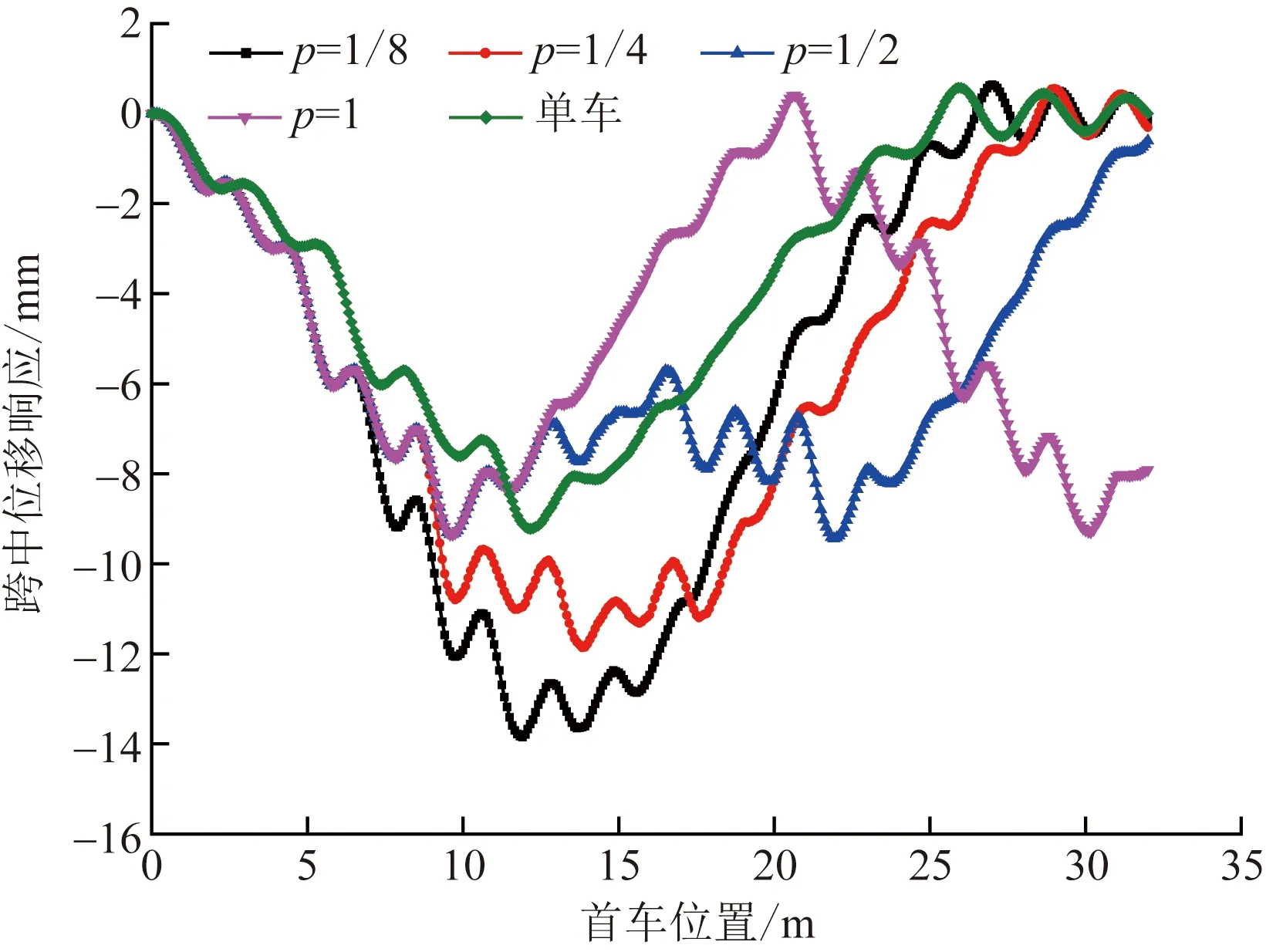
图9 不同车辆间距比桥梁跨中位移响应
4.2 不同车辆数量桥梁位移响应分析
因此,本文分析不同车辆在不同车辆间距下,通过简支梁桥时桥梁位移响应情况[15]。通过选用2~6辆车作为研究对象,结合单车通过桥梁时车速对桥梁振动响应的影响,选用60 km/h作为车辆行驶速度,分析不同工况下的桥梁振动响应,如图10所示。
根据图10可知,桥梁跨中最大竖向位移随车辆数增加而逐步增大,但车队中车辆数超过一定车辆时,桥梁跨中最大竖向位移不再增加,如当p=1/4时,车辆达到4辆车后,跨中位移达到极值,为13.51 mm, 为单车过桥时的1.4倍,两车过桥1.3倍,超过4辆车时,桥梁跨中最大竖向位移极值点不在增大。究其原因:随着车辆增加,桥梁的振动响应相互叠加,竖向位移逐渐增大;但当车辆数达到极值点后,由于车辆下桥时,桥梁阻尼系统对结构能量的耗散,与新驶入车辆对桥梁振动相互叠加,达到动态平衡,从而引起跨中竖向位移不在增大。
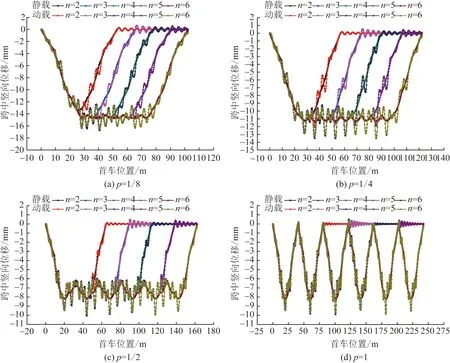
图10 不同数量车辆下桥梁跨中竖向位移时程曲线
4.3 多车车桥耦合冲击系数研究
通过对第4.2节相关数据进行整理,采用式(11)计算跨中截面位移冲击系数,并与不同国家规范冲击系数的规定值进行对比分析,如表4、表5所示。
由表4、表5可知:不同间距和车辆作用下,冲击系数计算值介于0.10~0.23;并与不同国家规范值进行比较,得到在车辆较多时,德国规范和中国规范的冲击系数小于仿真结果的最大值,其他国家的规范值大于规范计算值,表明:这两国规范在多车激励车桥耦合分析时,不太安全,建议在后续分析中,应考虑多车激励的影响。

表4 不同工况下跨中截面竖向位移冲击计算值

表5 不同国家冲击系数规范值
5 结论
(1)采用模态综合法建立多车的车桥耦合分析模型,通过与相关文献算例进行对比分析,结果表明:跨中位移响应计算结果相对误差均在6%以内,验证了方法的正确性和适用性。
(2)分析了车辆不同间距下,桥梁跨中截面竖向位移的时程曲线,即当车辆间距比减小时,最大竖向位移明显增加,当p接近1时,最大竖向位移接近单车时的位移响应。
(3)分析了在给定车辆间距下,不同车辆数对桥梁跨中截面竖向位移的影响。结果表明:桥梁跨中最大竖向位移随车辆数增加而逐步增大,但车队中车辆数达到极值点时,桥梁跨中最大竖向位移不再增加,其主要原因桥梁阻尼系统对结构能量的耗散,与新驶入车辆对桥梁振动相互叠加,达到动态平衡。
(4)通过计算不同间距比和车辆作用桥梁时,跨中截面冲击系数变化范围,并与多国规范值进行比较,得出在多车激励作用桥梁时,德国规范和中国规范的冲击系数偏于不安全,其他规范相对安全,建议在后续分析中,综合考虑多车激励的影响,相关研究成果可为公路桥梁多车车桥耦合分析研究提供参考。

