基于Fisher判别法的鸢尾花分类研究
赵清梦 周中洪
【关键词】Fisher 判别法;分类;SPSS 软件
研究鸢尾花的分类,原因是它对分类判别有着重要的意义。从形态上对植物的种类进行区分鸢尾花有很多种类,但有时肉眼也难以辨别,需要专业的知识才能对其所属的种类进行判断。因此研究鸢尾花的分类,根据鸢尾花的某些属性,建立有效的数学模型,对鸢尾花的种类进行分类十分重要。
鸢尾花的判别分析在最近几年逐步发展,代雪珍等[1]就逐步判别分析法在鸢尾花分类中的研究问题中提出运用判别分析法对UCI数据集中鸢尾花的数据进行分类,并得出该方法误判率小,拟合效果较好的结论;唐宇政[2]在基于欧氏距离的判别分析——鸢尾花分类问题探究中得出利用欧式距离判别法能较好地实现对鸢尾花的分类;康彩丽[3]在有导师学习的神经网络对鸢尾花种类识别中的应用中得到有导师学习的神经网络中的GRNN及PNN算法可以解决分类识别问题,具有一定的优越性,能很好地对鸢尾花进行种类识别。
一、Fisher判别法
Fisher判别法是判别分析方法之一[4]。它常被应用于多元分析,可以说判别分析是多元分析的一个分支。当有一个不知所属类别的样本时,可以使用判别分析计算其所属类别。判别分析的原理是根据一个既定的判断规则,构造一个或者多个判断函数,然后根据未知组别的大量的数据计算得到判断函数的系数,最后根据得到的判断函数计算未知样本所属类别。
根据判别标准的不同,可以将判别分析方法分为马氏距离判别、贝叶斯判别法、Fisher判别等。其中,Fisher判别法的核心思想是降维,用P维向量x=(x1,x2,...,xp)' 的少数几个线性组合y1=a'1x,y2=a'2x,...,yr=a'rx(一般r会远小于p)来替换最初的p个向量x1,x2,...,xp,从而达到降维的效果,最后利用这r个判别式y1,y2,...,yr判断样本所属的类别。
Fisher判别法存在以下的优势:若样本总体的平均值向量共线行较高,运用Fisher判别法会简化判断步骤,只需要几个判断函数就能判断样本所属的类别;并且Fisher判别法的使用不要求样本总体满足特定的要求,因而其应用的范围非常广泛。在使用Fisher判别分析法时不需要对数据进行特别的处理,因为其对样本本身没有特别的要求,同时还可以利用SPSS软件进行数据处理,提高计算的正确率并能够消除数据量计算过大的缺点。
二、实验结果与讨论
(一)数据选取
本次数据选取为花朵种类及其特征的数据,将花分为训练集和测试集,通过训练集花种类的特征来判别测试集的种类。
已知花的种类为三类,共150朵,每个种类均50朵。每朵花都提取了四个特征,其中变量“sl”为花的萼片长度,“sw”为萼片宽度,“pl”为花瓣长度,“pw”为花瓣宽度。种类中:“Setosa”我们用“1”来表示,“versiclr”用“2”表示,“virgnica”用“3”来表示。
(二)数据分析
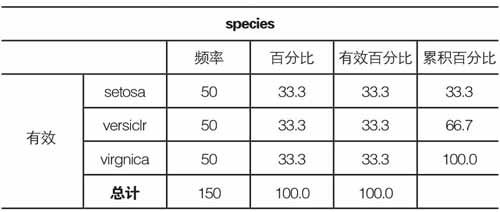
三、實验结果分析
鸢尾花的每个种类均有50个,我们选取每组40个作为训练集,10个作为测试集。本次的分类判别方法选用的是费歇尔斯判别法。 通过分类函数的公式可以计算得出判别结果,最终得到在本次试验中,对测试组的判别为100%。
四、结论
判别分析是根据观察或测量到的若干变量值判断研究对象如何分类的方法。判别分析是在已知分类数目的情况下,根据一定的指标对未知的数据进行归类。本文运用总体的Fisher判别分析法对鸢尾花的数据进行分类,结果显示其误判率非常小,拟合效果很好,说明能够依据鸢尾花的花萼和花瓣的长度和宽度建立Fisher判别模型进行判定,可以解决判别样本的问题,这为未知鸢尾花的分类判别提供了统计学上的理论依据和发展思路。

