基于改进 U-Net 网络的混凝土表面裂缝分割

甘 霖，谢爱荣，燕 阳，王 威，熊仕勇

(1.重庆市渝中区党政信息中心，重庆 400010；2.中国人民解放军陆军工程大学 通信士官学校，重庆 400035；3.重庆邮电大学 软件工程学院，重庆 400065)

0 引 言

截至2018年底，我国公路总里程已达到484.65万公里，高速公路里程达到14.26万公里。在混凝土公路里程快速增长的同时，也产生了极大的维护及保养压力。混凝土路面在大型车辆碾压或自然损耗之后，极易产生裂缝及破损，且随着时间推移道路状况会急剧恶化，最终威胁行车安全。针对现有人工检测存在的效率低下、漏检误检率高、时效性差等问题，如何在破损形成初期快速检测以帮助后期预防性修补成为了当前点一个研究热点。

现有研究主要以基于传统光学的数字图像处理方法为主，在利用成像仪器拍摄后对裂缝照片进行处理并以此为基础进行判断，常用方法有：①基于阈值的分割算法：此类算法通过裂缝区域与正常路面之间的灰度差，通过设定阈值进行划分，代表方法有OTSU分割[1]等；②基于裂缝边缘检测的分割算法：针对裂缝图像的灰度有明显的阶跃现象，可以此为边缘特征进行分割，如Canny[2]，Sobel，Prewitt，Kirsch，Roberts[3]等；③渗流法：通过构建渗流模型(percolation model)[4]，对每一个像素点分别对应一个局部窗口并运用区域生长算法进行生长，同时根据生长的结果来确定这个像素点是否为裂缝；④神经网络：随着近年来以人工神经网络为代表的机器学习技术的快速发展，在图像分类[5]、目标检测[6]、自然语义分割[7]等数字图像处理领域取得了突破性的发展。Long等[8]首先于2015年提出了全卷积网络(fully convolutional networks，FCN)用于图像分割，Ronneberger等[9]在FCN的基础上进行拓展并提出了U-Net网络，将采样前后的特征以拼接的方式进行融合，被广泛应用于图像特征领域。

但在混凝土表面裂缝分割方面，因为裂缝形态微小、细长的特点，在数据图像中所占像素比例较小[10]，使得裂缝图像成为了一个正负样本分布不均的数据，传统模型在此之上较难收敛。

本文针对现有模型在混凝土裂缝这类正负样本不均的数据集中学习效率低下的问题，以U-Net为基础，通过结合Focal[11]与活动轮廓模型[12]构建了一种新的损失函数，以适应正负样本分布不均的数据，并向U-Net模型添加批标准化层帮助模型训练，最后对训练得到的模型进行剪枝与量化[13]，便于部署于机器人等嵌入式设备。仿真实验表明，本文方法在同等条件下具有更高的分割精度。

1 裂缝分割模型

针对所述存在的裂缝正负样本分布不均而造成的模型收敛较慢、分割效果欠佳的缺陷，本文以U-Net模型为基础进行了改进。

1.1 分割任务描述

在机器学习领域，裂缝分割问题可以抽象为一类图像分割问题，即将待分割图像分割为健康区域与裂缝区域，所以可构建一个图像像素点分类模型h(·)。记给定长宽分别为w，h，图像I中所有像素点集合为P={px,y|0≤x≤w,0≤y≤h}，对任意h(px,y) 满足

(1)

若以交叉熵描述当前模型的预测效果，则有

L=-(px,ylog(p)+(1-px,y)log(1-p))

(2)

(2)式中，p为模型h(·)预测当前像素为裂缝的概率。

1.2 改进的U-Net模型结构

U-Net是由Ronneberger等[9]于2015年提出的一种图像自然语义分割模型。模型通过卷积与池化进行下采样，再通过反卷积进行上采样，激活形状相等的层之间添加残差连接进行拼接，增加特征维度，使得网络形状类似于英文字母U。模型输入为一张待分割图像，经过推理后的输出激活为原始大小、仅包含一个通道的分割结果。

该模型赢得了ISBI cell tracking challenge 2015，同时也被广泛应用于图像分割领域。U-Net中下采样由卷积块构成，结构如表 1，U-Net卷积块结构示意图如图1。

图1 U-Net卷积块结构示意图Fig.1 U-Net convolution block structure diagram

表1 卷积块结构Tab.1 Traditional convolutional block structure

为了帮助模型收敛，提高激活效果，本方法在池化层之前进行一次批标准化，结构如表2。

表2 本文卷积块结构

通过引入批标准化层能够将卷积层的激活归一化，提高激活函数的激活效果，防止梯度消失与梯度爆炸的产生，使得训练过程更加平稳，帮助模型学习裂缝特征，减轻过拟合与欠拟合风险[14]。本文卷积块结构示意图如图2。改进后的模型最终结构如图3。

图2 本文卷积块结构示意图Fig.2 Convolution block structure diagram of this paper

图3 本文改进后的 U-Net模型Fig.3 Modified U-Net model

1.3 损失函数

在研究过程中发现，现有分割模型在裂缝监测任务中表现往往欠佳，这是由于裂缝数据集中，裂缝区域所占面积往往较小而造成正负样本分布不均的问题。若直接训练，则会导致模型在训练过程中简单地预测数量更大的正常路面即可获得较高的准确率，无法正确地学习裂缝的特征。因此，本文在现有的研究基础之上，通过结合Focal损失与活动轮廓(active contour)构建一种针对样本不均衡问题的损失函数。

1.3.1 Focal 损失函数

Focal损失函数是由Lin等[11]于2017年提出的一种针对正负样本分布不均的损失函数。如(2)式所示传统的交叉熵损失在裂缝分割任务中，因为正负样本极度不均会直接导致无法训练的状况，因此，一种解决方法便是为不同类别的损失函数使用不同的权重，使得模型能够专注于小样本的特征。设正类样本系数为α，则负类样本系数为(1-α)，对应的交叉熵表示为

CrossEntropy(pt)=-αlog(pt)

(3)

(3)式中，pt是调制因子。而Focal损失函数为了增强模型泛化能力，强迫其学习难分样本特征而引入了动态缩放系数γ，将易分样本的贡献缩小、难分样本的贡献增大。因此，pt可以表示为

(4)

对于正样本，调制因子是p；对于负样本，调制因子是1-p。最终的Focal损失函数定义为

Lfocal=-αt(1-pt)γlog(pt)

(5)

1.3.2 活动轮廓损失函数

活动轮廓模型又称“Snakes模型”，其通过在图像创建一条初始曲线，将目标物体轮廓线包在内侧。通过构建的“能量方程式”，包括规范内的曲线形状称之为目标的“内部能量”，将规范曲线与目标物体轮廓线接近程度称为“外部能量”。在运算过程中，最小化内部能量可令曲线持续向内部紧缩并保持平滑；而最小化外部能量则可令曲线持续贴近目标物体轮廓线而到达一致为止。该方法为计算机视觉领域的常用方法之一。

Chen等于2019年提出了一种基于活动轮廓的损失函数，其形式为

LossAC=Length+λ·Region

(6)

(6)式中，Length与Region分别代表周长与面积，分别表示为

(7)

(8)

(7)—(8)式中：u代表分割结果；v代表图像标签；x,y分别代表在水平与垂直方向上的分量；Ω为图像域；c1与c2为活动轮廓模型的内部能量(前景)与外部能量(背景)；ε为一个十分小的值，防止被开方变量为0。

1.3.3 一种结合Focal损失与活动轮廓损失的损失函数

本文为了增加模型在训练过程中对裂缝的敏感程度，加快模型收敛速度，设计了一种新的损失函数，将Focal损失函数与活动轮廓损失相结合，以期适应正负样本分布不均数据的同时，保持对数据学习容易程度足够的敏感性。其形式为

Lossnew=Lfocal+β·LAC

(9)

(9)式中，平衡系数β为一个值域为[0,1]的常数，用于平衡二者，本文β取值为1E-4。

1.4 模型的剪枝与量化

为了将本文提出的裂缝分割模型部署于机器人等嵌入式平台中，还需对模型进行权重剪枝及量化。

权重剪枝即消除模型中不必要的权重，将模型中的张量转化为稀疏张量，以便于模型的压缩。

模型训练过程中，往往会产生大量数值非常小且无用的权重，一方面其在推理过程中因其权重值过小无助于推理过程；另一方面因其数值不为零无法直接压缩，所以本文通过在迭代过程中不断将最接近于0的权重置0，直到达到设定的稀疏度，以实现剪枝。

模型权重数据在PC中通常以32位浮点数的方式存储，而嵌入式环境通常没有图像处理单元，故需将模型量化为8位整数，以便嵌入式设备的CPU计算。

2 仿真实验

本文在训练过程中采用Dice系数作为评价标准，其形式为

(10)

Dice系数代表预测结果与原始图像的相似度，数值越高，则表示分割越准确，算法性能越好；反之，数值越低，越不准确，算法性能越低[15]。

同时，也使用准确率(ACC)、F1分数、平均交并比(IoU)指标评价模型。

实验共4组，分别为①传统U-Net+Focal损失；②传统U-Net+新损失；③改进的U-Net+新损失；④c组训练完成后剪枝。

2.1 实验内容与环境

为保证对不同场景中的裂缝进行客观评估，训练集与测试集由CFD[16-17](118张)，CRACK500[18](3 363张)，CrackTree200[19](206张)，DeepCrack[20](521张)等4个公开数据集与自建数据集(311张，Nikon D3100拍摄，距离地面约1.5 m，光圈快门自动，截取为256×256像素裂缝图片)共同组成。输入尺寸为256×256像素，预处理期间对原始数据进行旋转、平移等扩增，并保存为灰度图像，训练集67%数据用于训练，33%用于验证。当模型训练时损失的梯度连续5次小于预设阈值视为收敛。

在训练完成后，从未使用数据中随机选取7张裂缝图像并使用各个模型对其进行预测。将原始图像、各模型预测结果与人工分割图像进行对比，结果如图4。

实验硬件环境为Intel Xeon CPU 2.2 GHz x2，24 GB内存，Tesla K80 (14G)显卡。软件环境为TensorFlow r1.14，TensorFlow Lite，TensorFlow Model Optimization。

2.2 结果分析

2.2.1 各模型分割结果分析

各模型训练时在验证集上的损失如图5。由图 5易见，本文的改进U-Net模型与新损失函数组合(见图5c)相较于其他对照组收敛更加平滑、稳定。

图5 各模型训练过程中loss对比Fig.5 Loss comparison during training of each model

各模型前100轮训练过程中在验证集上的Dice系数变化如图 6。

图6 各模型训练过程前100轮中Dice系数对比Fig.6 Comparison of Dice coefficients during first100 epochs training

原始U-Net+Focal损失(见图4b)在训练初期十分不稳定，产生了激烈的震荡，在测试图像中将部分斑点错误识别为了裂缝；传统U-Net+新损失(见图4c)通过在损失函数中加入活动轮廓损失，能够部分抑制震荡的产生；本文提出的改进的U-Net+新损失(见图4d)对应的训练过程平滑且稳定，且收敛后上界相较于传统U-Net模型有一定程度的提升。

图4 实验结果对比Fig.4 Comparison of experimental results

通过本文方法(见图4d)与对照组图4b，图4c的对比可以发现：训练初期0—20轮迭代时，本文方法更加稳定；训练中期20—60轮迭代时，本文方法收敛速度明显快于图4b组，较图4c组更加稳定、平缓；训练末期60—100轮迭代时，本文方法的Dice系数收敛于99.64，高于图4b组的99.02与图4c组的99.43。

各模型预测结果见图4，图4b组在图(1)，图(4)，图(5)中离散点显著多于图4c，图4d，证明本文提出的改进损失函数中活动轮廓能够从形态上约束分割。分别计算各模型对应的ACC，F1分数与IoU，得到表3。易见本文所提出的改进模型与新损失函数组合在上述3项性能皆远高于传统方法。证明本文方法针对混凝土表面裂缝具有更高的性能与泛化能力。

表3 各模型性能综合指标对比

2.2.2 剪枝及量化前后对比分析

在图4d组完成训练后，先对其进行剪枝，通过20轮训练，将模型各层权重张量中最接近0的权重置0，使得模型整体稀疏度接近目标值0.9。剪枝完成后，为了便于在嵌入式设备中部署本模型，再将各权重由原本的32位浮点数量化为8位整数存储。

取剪枝前后模型的前4层卷积层权重，将其重塑为二维张量，并绘制对应的热力图，如图7。

可以看出，通过剪枝后权重张量具有更高的稀疏度，便于后期对模型进行压缩。分别计算原始模型、剪枝后模型与量化后模型在压缩前后的大小，结果如表4。

表4 剪枝前后模型大小对比Tab.4 Comparison of model size before and after pruning MB

通过表4易见，剪枝与量化能够极大程度上压缩模型，便于在嵌入式设备等空间受限环境中的部署。

剪枝后的模型测试结果见图7，对应的性能指标见表3。相较于剪枝前分割性能有一定下降，但仍好于图7a，图7b。

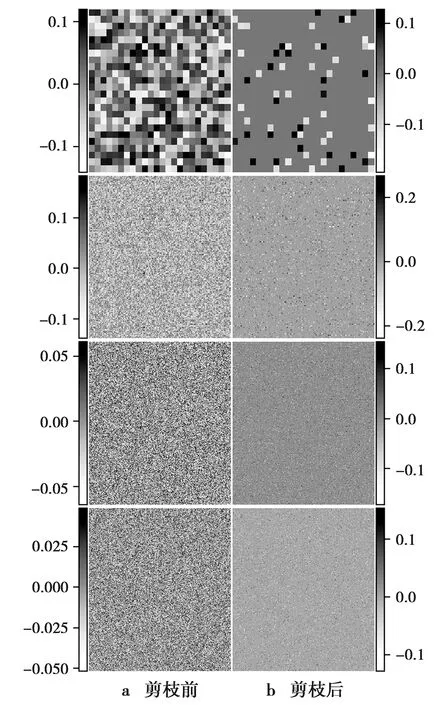
图7 剪枝前后权重对比热力图Fig.7 Heat map comparison between before and after pruning

3 结束语

本文针对混凝土表面裂缝的特殊性，在现有深度学习领域U-Net图像分割模型的基础上，针对其无法满足正负样本分布不均的问题，通过改进模型结构、构建新的损失函数使之能够高效、稳定地学习裂缝特征。同时通过剪枝与量化使得模型能够适应机器人等嵌入式设备。试验结果表明，本文方法针对现有方法的不足，能够准确学习混凝土表面裂缝的纹理、结构特征，具有准确度高、性能优异等特点；同时，本文方法亦可推广于其他正负样本分布不均的图像分割问题中。