能得见计算的拼图
陈凯
“计算”一词在不同语境下有不同的含义,即便是将范围严格限定于“用机器进行自动计算”这样狭窄的场景之中,其含义也是丰富多彩、变化多样的。考虑这样一个简单的需求,计算第一项为1,且第二项为1的斐波那契数列第n项的值,如用户输入的是数字6,而机器给出的是对应的第6项斐波那契数列的值8,显然,机器的确进行了计算,可要是深究其“计算”的含义,却有如下不同。例如,机器可能只是预存了整个斐波那契数列,对于输入的n,它实施了一个查找数据的工作。考虑人类在做8加7得15,或做8乘以7得56的计算的时候,人的头脑事实上所做的也是这种查找数据的工作,毫无疑问这是一种计算,然而对于这个计算机器的使用者来说,它是如何查找和匹配数据的,其过程是一个黑盒,是不可见的。又如,机器可能是根据斐波那契数列的通项公式来进行计算的,而通项公式的由来,是经由观察、归纳、假设、证明、演绎等一系列数学工作的结果,在具体使用通项公式时,数学计算本身仍然是一个黑盒,使用者还是不知道,机器是如何实现对5开方等一系列具体计算步骤的。再如,机器可能是通过一个循环结构的程序来实现计算的,它首先计算了第一项和第二项的和,并将计算结果赋予第三项,然后再计算第二项和第三项的和,再将计算结果赋予第四项,在这个过程中,除了具体的加法计算过程是黑盒,循环结构的实现本身也是一种黑盒,显然,对于程序的编写者来说,他不知道循环语句和结构何以能发挥作用,他只是借助这些语句和算法结构发挥了作用而已。在上述所有的例子中,对于使用计算机器的人而言,“计算”要么是全部不可见的,要么是局部不可见的。
当然,无论是为了教学,还是为了某个实际的用途,将计算机器所有的计算过程都展现出来,是不现实的,也是不必要的。例如,在用循环结构的程序计算某个斐波那契数列项的时候,人们的头脑尚能跟踪高级语言环境中,每个变量或数组变量中值的变化,但若要在寄存器的级别上,跟踪用以实现循环和赋值操作的每个电信号的变化,就是相当困难的事了,更何况,求得斐波那契数列项的值只是一个很简单的程序。若要使得解决某个具体任务的整个计算过程清晰可见,不可避免要做到以下步骤:首先,需要知道编译程序是如何将这个高级语言程序代码转化成二进制机器语言的;接着,跟踪这个二进制机器语言的执行过程,继续往下深入,跟踪普林斯顿结构或其他结构的计算机器中的各个部件是如何协调工作,执行这些可实现循环功能的机器代码的;然后在更底层,了解数字电路是如何实现逻辑运算和数学运算的……如果能将整个蓝图展现出来,计算便是可见的,但显然,即便是将很简单的高级语言程序按上述过程全部展开,其规模也庞大到让人的头脑无法进行跟踪,所以就结果而言,计算过程仍然是部分不可见的。
在工业设计上,人们采用的是模块化和层层封装的方式,来构造具有特定功能的计算机器。但在教学上,人们面对的是盒子里套盒子层层叠叠一时无法穷尽到底层的窘境。然而,为了理解某个问题,人的头脑并不需要真的像机器那样,去跟踪所有的电信号或机械状态的变化。因为从直观上说,当人们发现一个小型的系统是以某种模式进行计算的之后,就能直观推断,一个以类似结构搭建的更大型的系统,也应该能以同样的模式进行更大规模的计算。举例说,计算28加7,人的思维过程是从记忆里找出8加7所对应的15,然后低位写5,高位进1,很容易判断,对于更大的数字,如280+70,采用的方法也是类似的,这其实就是一种模式的识别和匹配。人的头脑能够直观地认识到,一个较小数字的可行的计算模式,是可以套用到更大数字上的(这里暂不讨论用小规模的计算系统实现普适计算的问题,因为那涉及用一种计算模型去模拟另一种计算模型的问题)。要想让学生理解计算之所以可行,就需要通过一个小型的计算系统的运作过程,建立起关于“计算”的直观概念。
因此,当前的任务,就是找到一个可以进行计算的小型系统。这个系统需要满足以下特征:一、能演示自动化的工作流程,或者稍加改造就能演示自动化的工作流程;二、运行过程能体现出计算思维的特征,如抽象化、形式化、模块化等思想;三、运作过程是完全可见的;四、能完成某个具体任务,并且,从直观上看,它具有经由改造后完成其他任务的潜力;五、考虑到教学资源、课时等因素,对其的讲解和操作不需要依赖太多其他专业方面的知识。为了满足以上五点要求,可供选择的小型的计算系统范围被大大缩小。虽然说一个小型的电子电路系统基本上也能契合上述大部分要求,但以信息技术学科“过程与控制”模块中有限的电子电路内容看,是难以用来展现稍微复杂一些的具有计算思维特征的运作过程(如迭代、递归等)的。图灵机虽然极为符合以上一到四点的要求,但若要让学生们对其工作过程真正理解,需要耗费较多时间进行讲解和操作训练。
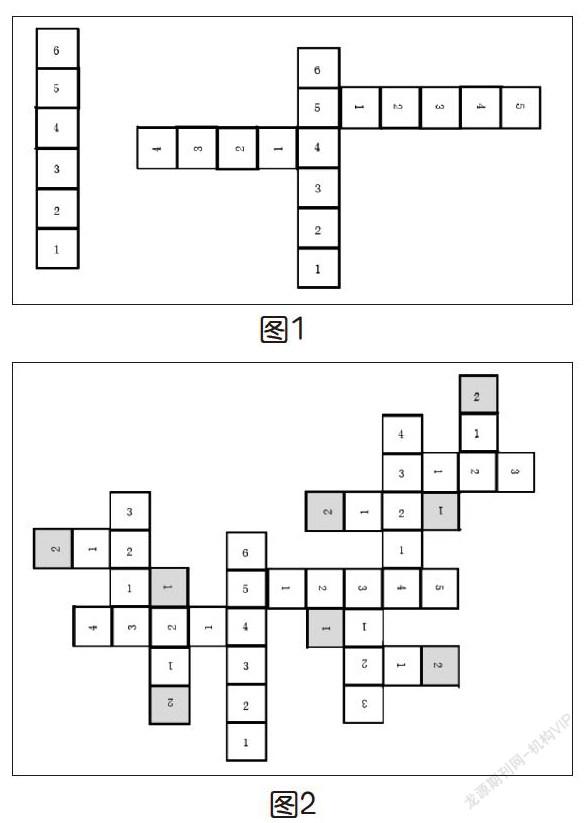
这就促使笔者设计出一种拼图游戏来充当这样一个小型的计算系统。游戏有很多种变化形式,下面是一个可计算斐波那契数列项的拼图游戏,拼图是一些不同长度的条状纸片,纸片上分出格子并按自然数顺序标上数字。每个拼图就好像太空站一样,在最大数字的格子的下方两个格子上各留出了两个对接接口,用于拼接那些最大数字和格子号码相同的拼图。拼图的最大数字是n,则接口的位置在n-1和n-2处。例如,对有6个格子的拼图,接口位置在5号格子和4号格子的位置,5号格子可以拼5个格子的拼图,4号格子可以拼4个格子的拼图。如果按这样的模式匹配,则计算过程一直能进行下去,直到所有的“空间舱”都无法满足继续拼接的要求,也就是说,不再能找到可匹配的模式,计算过程自然而然就停止了。显然,拼接工作终止于最大数字是2或者1的拼图。图1显示了拼图的第一步,图2显示了完成后的整个拼图。
当每次使用到最大数字是2或是1的拼图时,可以用作标记的方法计数一次,可以看到,如果最初使用的拼图的最大数字是6,则整个拼图完成后,计数值是8。这其实就是计算了第6项的斐波那契数列的值为8。整个过程对应用递归的方法来计算斐波那契数列的过程:为了计算第n项的斐波那契数列的值,则需要先计算第n-1项和第n-2项的斐波那契数列的值,此过程一直持续下去直到遇见第二项和第一项的斐波那契数列的值为1。可以看出,拼图游戏能体现出解决具体问题中计算思维的特征,整个运作过程是完全可见的,拼接过程中并不涉及其他专业知识。虽然说拼图过程并不是全自动化进行的,但一旦规则设定好,即便是手工操作,其结果也是必然的。这里可以鼓励学生对拼图进行改进,如留出特定宽度的拼接凹凸接口,这样,即便不对照数字的大小,也能将拼接过程进行下去。
拼图游戏的一个很重要的优势是,拼接规则是可以方便地进行扩充和改造的。不妨思考这样的问题,如果设计一台计算机器,那么它将如何自动完成图形的拼接,并由此实现斐波那契数列项的计算?关于自动机器实现拼接过程中可能遇到的麻烦,以及如何使得自动拼接成为可能,可以开展一次头脑风暴活动。关于機器实现自动拼接中的困难,这里试举一项:计算机中比较容易实现的数据存储方式,是一系列前后相邻的存储单元,于是就产生出问题,即二维空间上的拼图,如何转化为一维的数据存储方式。
显然,在一维的数据存储空间中,拼接过程要通过符号模拟来达成。具体方案很多,如用“#”代表拼图,“*”代表等待拼接,“^”代表拼接完成,一种可能的操作规则和操作过程如下表所示。
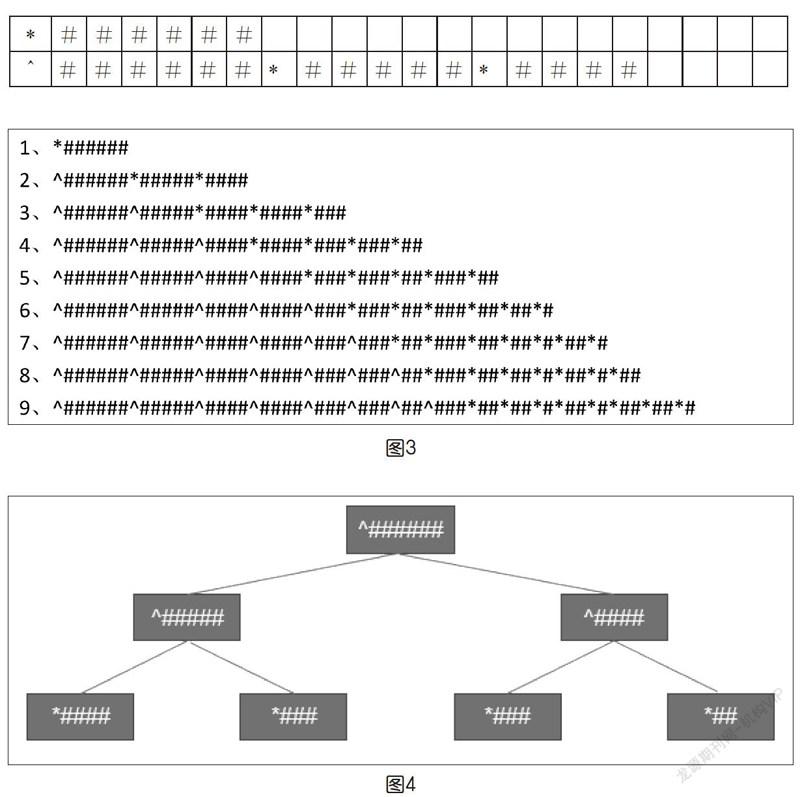
下表表示了6个格子的拼图拼接上5个格子和4个格子的拼图的过程,每次拼接完成后,“*”变为“^”符号,表示处理完成。整个拼接过程中,总是按遇见n个格子则在最后拼接n-1个格子和n-2个格子的规则进行,如果遇见的是2个格子和1个格子的拼图,则只是简单拼接上和自己相同数量的格子的拼图(为了简化问题,这个匹配过程没有考虑停机问题,可以引入新的符号来实现停机的匹配规则),整个变化过程用字符串描述如图3所示。
第9步之后,拼图中“*”的数量不会再发生变化,而“*”的个数则对应着相应第6项斐波那契数列的值。并且,还能有办法看出不同拼图之间的关系:第1块拼图拼接的是第2和第3块,第2块拼接的是第4和第5块,第3块拼接的是第6和第7块,以此类推。当然,这样的表示方法很不直观,如果以树的形状将拼图之间的关系呈现出来,则要清晰得多,图4是第4步拼接操作完成时所显示出的拼图之间的关系。于是这里又引出了新的问题,如何能更合理地借助一维的存储空间,使得机器能方便地识别出拼图之间的关系,同时,也能让人更容易将存储空间里的数据转换成人更能理解的图示?这就很自然地从如何实现自动计算的问题,指向了数据结构的研究。
至此我们可以看出,借助拼图游戏,不仅使得计算的过程变成可见的,而且也使得自动计算中,解决问题的思维方式成为可见的。关于如何使计算过程可见,进而如何使计算思维可见,方法必然有很多种,本文权当抛转引玉,希望能激发出大家的思考欲望。

