基于改进GO-FLOW法的核电常规岛给水系统可靠性在线评价
张小勇,魏振华,林令知,柴雨桐,杨国田
(1.国核电力规划设计研究院有限公司,北京 100095;2.华北电力大学 控制与计算机工程学院,北京 102206)
0 引 言
核电机组的可靠性一直受到高度关注。诸多学者针对核岛反应堆[1-4]、常规岛汽轮机[5-7]、核电电力系统[8]、给水系统等重要系统[9-12]进行了可靠性研究,形成概率安全评价(PSA)体系[13,14],提高了核电机组整体安全性。
核电可靠性分析方法以故障模式及影响分析、故障树分析及可靠性框图为代表用于早期核电机组的安全评价中,该分析方法多为静态分析方法[15,16]。由于该类方法对复杂系统的可靠性计算较为困难且准确度较低,进而有学者提出采用故障树最小割集与蒙特卡罗法相结合的方法进行可靠性分析[17-19],但这些方法无法动态评估系统可靠性。针对这一问题,有学者提出了动态事故进程树分析方法[20,21]、故障树模型转换为Markov模型[22,23]、神经网络[24,25]和GO-FLOW法[26,27]等动态可靠性分析方法。这类分析方法虽然可对系统进行动态可靠性分析,但分析过程中提取的设备可靠性参数仍多为设备厂家提供的静态数据,无法全面代表设备真实状况。
随着对核电厂机组安全性要求的不断提高,现有可靠性分析方法已无法满足机组实时安全状态评价[28]。亟需研究实时动态可靠性分析方法,快速准确地进行机组安全评价,降低核电机组运行风险。常规岛给水系统作为核电机组重要组成部分,其可靠性影响着核电机组安全稳定运行[29,30]。目前给水系统可靠性分析中,未建立能表征系统运行状态的动态模型;而且系统中各设备可靠性参数是由厂家提供或根据经验所得[31-33]。由于各个设备所处运行环境的差异和故障程度不同,导致设备可靠性参数会发生变化。若不动态修正可靠性参数,则可靠度计算就会出现偏差,进而影响了可靠性评估的准确性。
针对上述问题,本文提出一种基于熵权Topsis和灰色关联度改进的GO-FLOW法并应用于核电机组常规岛给水系统可靠性在线评估,可修正系统设备在不同状况下可靠性参数,准确计算系统各状况下的可靠度。针对给水系统多部件多故障的特点,采用基于人工鱼群优化的支持向量机建立给水系统故障诊断模型,当诊断结果为有故障时,基于熵权Topsis和灰色关联度对系统故障元件状态进行评估,根据评估结果修正故障元件可靠性参数;当诊断结果为无故障时,保留元件原可靠性参数。将元件可靠性参数输入GO-FLOW模型中,获取给水系统可靠性在线评估结果。
1 改进GO-FLOW法
1.1 方法整体概述
GO-FLOW法是一种以功能流为导向,将系统工程图按一定规则转化成为GO-FLOW模型,进而可定性或定量分析系统可靠性方法。该方法可用于时间相关的系统可靠性分析。
基于改进GO-FLOW法的系统可靠性实时评价框图如图1所示。首先实时采集运行参数并输入至系统故障诊断模型中,进行故障诊断。若诊断为有故障,则根据对应设备评价指标,采用熵权Topsis和灰色关联度对设备进行状况评估,根据评估结果修正对应设备的可靠性参数。将修正后可靠性参数输入至GO-FLOW模型中,计算当前状况下系统可靠度。若诊断为无故障,则输入各设备原可靠性参数到GO-FLOW模型中,进行系统可靠度计算。由此实现系统的可靠性实时评价。

图1 基于改进GO-FLOW法的系统可靠性实时评价Fig.1 System reliability evaluation in real-time based on improved GO-FLOW method
1.2 故障识别
故障诊断模型采用基于鱼群优化算法的支持向量机(Artificial Fish Swarms Algorithm-Support Vector Machine,AFSA-SVM)实现,即由支持向量机实现故障诊断与分类任务,而鱼群算法完成支持向量机的参数寻优。
鱼群算法原理是:通过人工生成鱼群对SVM中的参数惩罚因子c和核函数参数δ进行寻优选择,达到优化分类的效果。其中惩罚因子c决定了分类间隔大小以及分类的准确程度,表示了分类中对误分类的惩罚大小。核函数既能将分类效果表现在了高维上,同时避免了在高维空间中的复杂计算。此次分类中核函数为径向基核函数为
(1)
该函数对参数十分敏感并且对数据中存在的噪声有着较好的抗干扰能力,还有很强的局部性,参数δ决定了函数作用范围,并随着参数δ的增大而减弱。算法流程如图2所示。
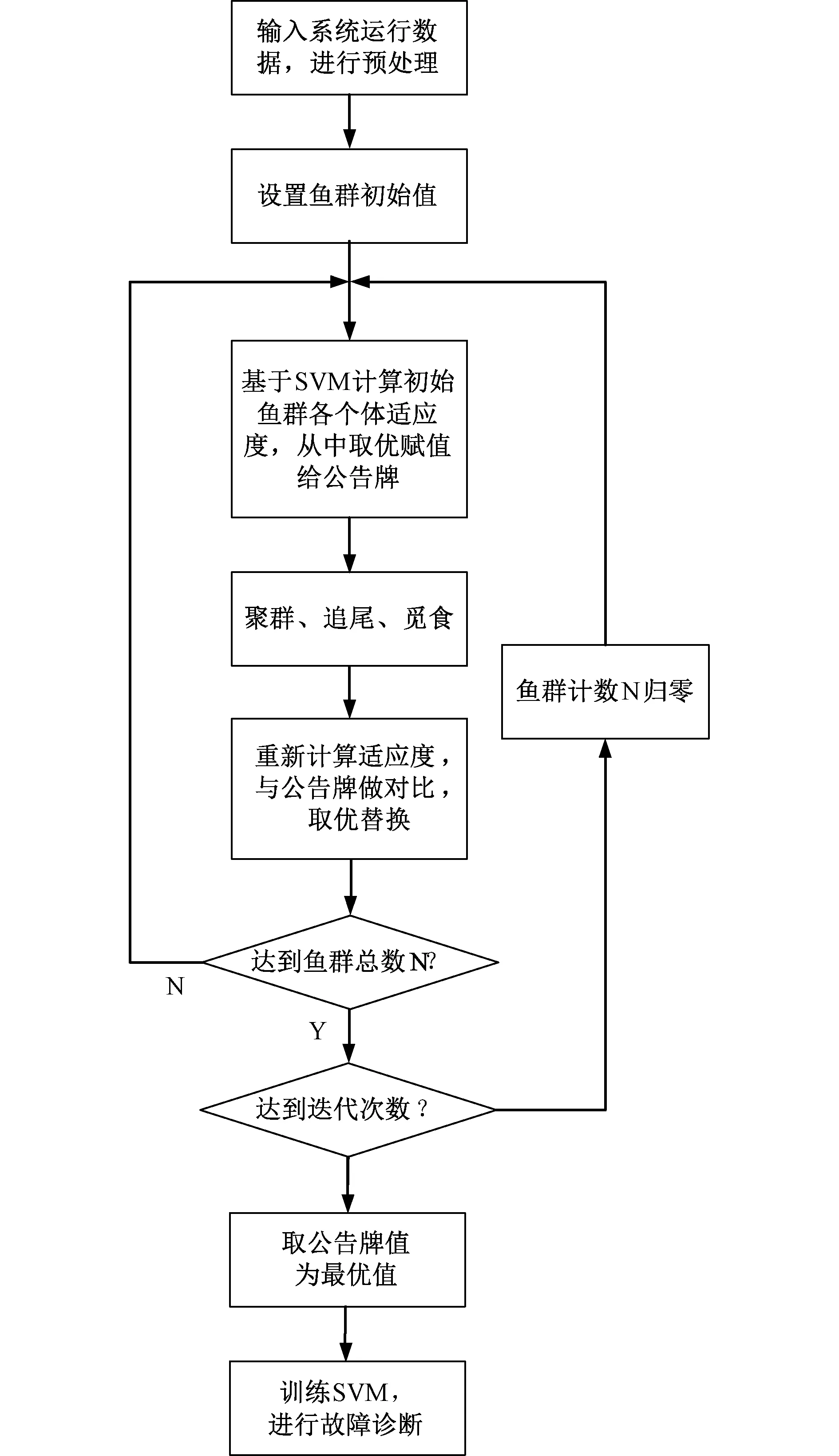
图2 AFSA-SVM算法Fig.2 AFSA-SVM algorithm
选取涵盖所有故障的n个训练样本和k个测试样本对故障诊断模型进行训练和测试,使得给水系统故障诊断模型可以通过测点数据诊断出系统有无故障以及故障类型。具体实现见后文。
1.3 改进GO-FLOW法原理
改进GO-FLOW法与原GO-FLOW分析方法不同处在于:根据设备状况,实时修正设备可靠性参数。当诊断模型诊断出系统有故障时,采集该故障状况下系统的运行数据,对应评价指标对数据进行预处理,从而得到指标矩阵;然后利用熵权法获取各指标权值,并与指标矩阵相乘得到加权标准化矩阵,从而求得正负理想解;最后采用欧氏距离与灰色关联度相结合的方法得到设备可靠性参数修正系数。将修正后的设备可靠性参数输入系统GO-FLOW模型中,计算可得该故障状况下系统实时可靠度。
对设备状态进行评估,首先对应各个状况的各个指标进行统计打分,得到指标矩阵A(aij)m×n,并对指标矩阵进行规范化处理得到B=(bij)m×n,其中,m表示系统运行数据组个数,n表示指标个数,i=1,2,…m,j=1,2,…n。
用熵权法确定各指标的权重,首先得到第j个指标的熵值xj,其计算式为
(2)
然后可得第j个指标的熵权rj,其计算式为
(3)
式中:i=1,2,…m,j=1,2,…n。
将规范化后的指标矩阵乘以对应的指标权重形成加权标准化矩阵Y(yij)m×n,确定每一个指标集合的最大值和最小值,以Y0+表示正理想解,Y0-表示负理想解,其分别为
Y0+=(y1+,y2+,y3+,…yn+)
(4)
Y0-=(y1-,y2-,y3-,…yn-)
(5)
取某一状态下系统的运行参数组i,将其转化为加权指标矩阵yi,计算该状态到正、负理想解之间的欧氏距离Di+和Di-,其计算式为
(6)
(7)
式中:j=1,2,…n。
计算运行参数组i和正、负理想解之间的灰色关联系数,其计算式如下:
(8)
(9)
参数组i与正、负理想样本的灰色关联度Wi+、Wi-为
(10)
(11)
式中:j=1,2,…n。
对欧氏距离和灰色关联度进行归一化得到di+,di-,wi+,wi-,计算此设备状况与设备理想状况的相对贴近度εi:
Ti+=0.5di-+0.5wi+
(12)
Ti-=0.5di++0.5wi-
(13)
(14)
将得到的相对贴近度εi命名为设备可靠性参数修正系数ζ。由此可得该设备状况下的可靠性参数修正为P=ζ×Pg,其余设备可靠性参数为原可靠性参数。当故障诊断结果为无故障时,各设备的可靠性参数保持为原可靠性参数,即设备可靠性参数修正系数ζ为1。
2 可靠性评价
2.1 核电常规岛给水系统
某核电机组常规岛给水系统主要设备包括三台并联的33.3%电动定速给水泵组、四台50%容量的高压加热器[34,35]。系统中,三组给水泵作为整个给水系统的动力源,将除氧器中的给水加压输送至给水母管。四台高压加热器分为两级、双列,分别对给水母管中的给水进行加热。某核电站的给水系统简化结构图如图3所示。
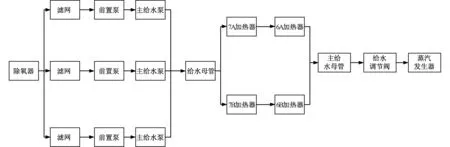
图3 给水系统结构图Fig.3 Structure of water supply system
2.2 可靠性模型
使用GO-FLOW方法直接把系统结构图转换为系统可靠性模型,所建可靠性模型如图4所示。
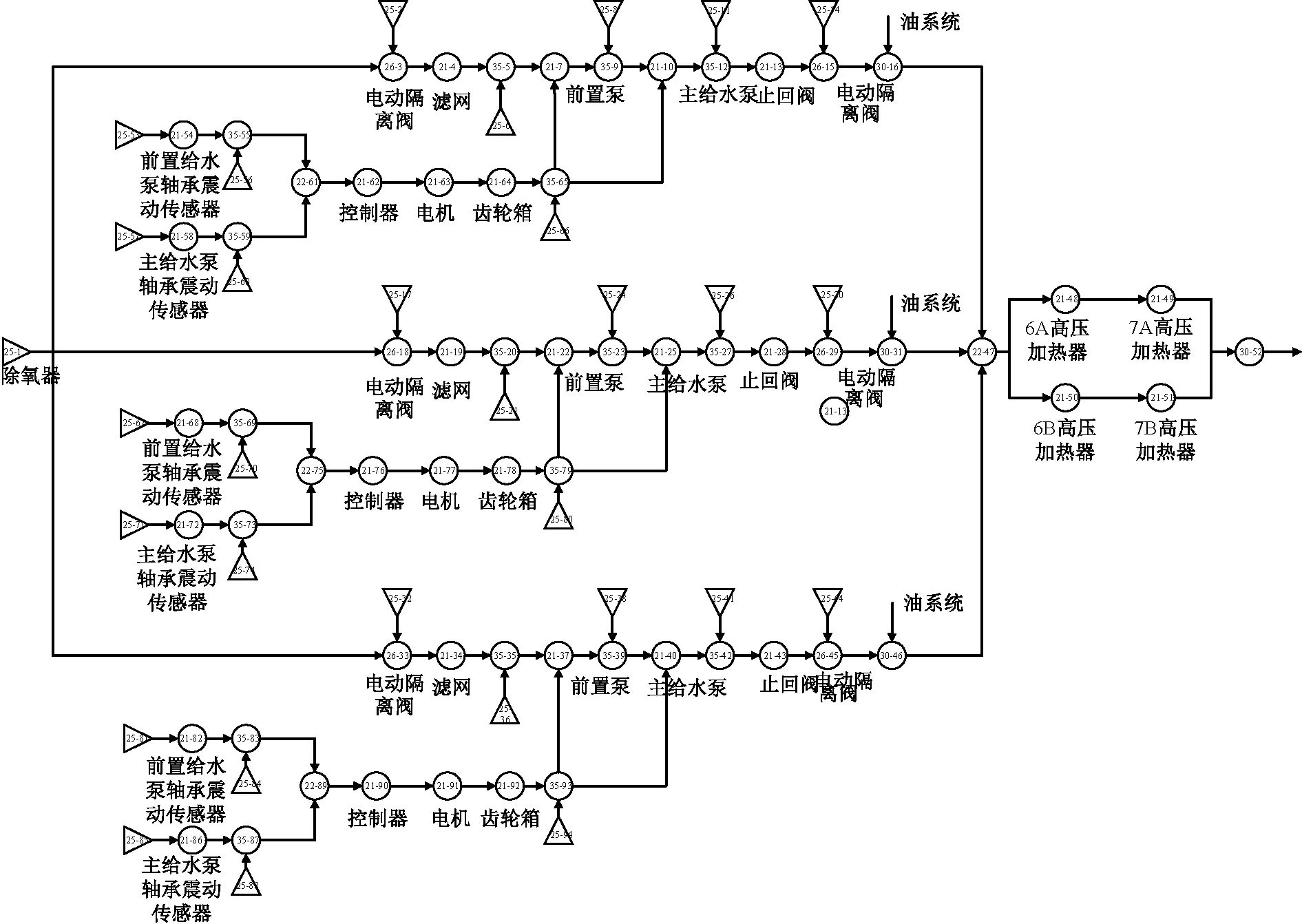
图4 给水系统 GO-FLOW可靠性模型Fig.4 Water supply system GO-FLOW reliability model
输入系统各个设备可靠性参数到给水系统GO-FLOW模型,从信号发生器开始,沿着信号线,按照运算规则,逐个计算操作符在各个时间点的输出信号值,即可得到系统可靠度。
首先,采集给水系统在100%工况下,13种故障类型和正常运行状态对应80个测点的样本数据,将采集到的数据对AFSA-SVM故障诊断模型进行训练。通过实时采集系统运行参数,可实现对给水系统实时故障诊断,并且诊断结果准确率为98.665%。所选故障类型如表1所示。

表1 给水系统故障类型Tab.1 Water supply system failure type
根据故障诊断结果对给水系统进行可靠性评价。当故障诊断结果为无故障时,给水系统的可靠度随时间动态变化计算结果如图5所示。
以成功向蒸汽发生器输送给水作为系统成功的标准,按照系统每运行1 000 h为单位设置5个时间点。从图5中可以看出,在运行开始时系统可靠度为99.999 1%,随着运行时间的增加,由于设备性能缓慢退化而造成系统可靠度呈缓慢下降趋势,这就是采用GO-FLOW方法分析与时间关联的系统可靠性原因。

图5 给水系统无故障时系统可靠度Fig.5 System reliability when water supply system is fault-free
当故障诊断结果为有故障时,以各状况下的给水系统运行参数为基础,对应提出的状态指标,根据给水系统的功能要求和控制逻辑选择设备状态评估的指标:四台加热器水位、给水母管水压、设备故障引起测点波动数、测点波动幅度、测点值上升速率、设备维修时间、系统已运行时间。对应评估指标对系统进行打分,形成指标矩阵形成指标矩阵A(aij)m×n。对指标矩阵进行归一化等规范化处理,得规范指标矩阵B=(bij)m×n,其中指标数n为7,数据组个数m为14,如表2所示。
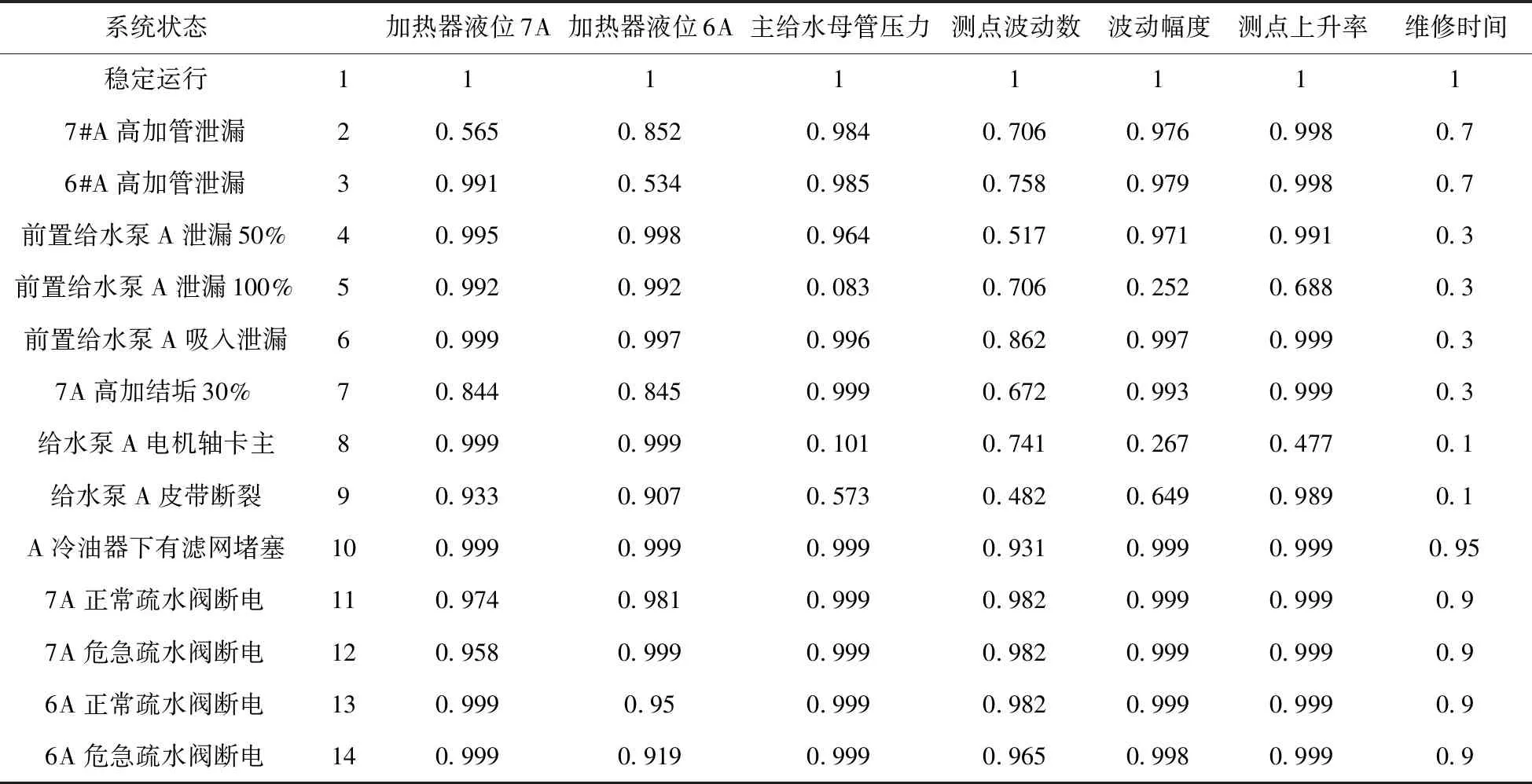
表2 规范化指标矩阵Tab.2 Normalized indicator matrix
采用熵权法得到各指标的权重并与矩阵B=(bij)m×n相乘,得到加权标准化矩阵Y(yij)m×n如下所示。

由指标矩阵Y得出应的正理想解为Y0+=(0.691,0.640,0.499,0.494,0.500,0.567,0.485),负理想解为Y0-=(0.001 8,0.021 3,0.133 2,0.161 3,0.133 2,0.046 3,0.197 2)。
通过公式(8)、(9)、(10)、(11)求得各故障类型所对应的欧氏距离和灰色关联度值,然后根据公式(12)、(13)、(14)得出各故障类型与理想状况的贴近度,如表3所示。

表3 各故障可靠性参数修正系数Tab.3 Correction factor of each fault reliability parameter
根据所得对应故障与理想状况贴近度,可得该设备的可靠性参数修正系数。以7#A高压加热器给水管泄漏故障为例,此状况下其可靠性参数修正系数ζ为0.639 3。将该修正系数输入给水系统GO-FLOW模型中,可计算出此时给水系统的可靠度计算结果如图6。

图6 给水系统有故障时系统可靠度Fig.6 System reliability when the water supply system is faulty
以成功向蒸汽发生器输送给水作为系统成功的标准,按照系统每运行1 000 h为单位设置5个时间点,其中时间点1、2为系统稳定运行状况,时间点3为系统发生7#A高压加热器给水管泄漏故障,且在时间点3之后的时间点4、5,为系统在不维修状况下继续运行。从图6中可以看出,时间点1、2,系统无故障且系统可靠度呈缓慢下降趋势(详参见图5)。时间点3,修正7#A高压加热器给水管可靠性参数后,系统可靠度下降至99.85%,相较于图5中系统稳定运行状况下时间点3的系统可靠度下降了0.145 1%,且在时间点3之后系统可靠度下降趋势且下降趋势变快。
通过给水系统稳定运行和故障状态下可靠性仿真结果表明:改进GO-FLOW法可以有效实现给水系统可靠性实时定量评价,同时通过熵权Topsis和灰色关联度相结合的方法修正故障设备可靠性参数,使可靠性评价结果更为准确。
3 结 论
针对核电机组常规岛给水系统,本文提出了一种可靠性在线评价方法。基于改进GO-FLOW可靠性分析方法建立给水系统时间可靠性模型,采用AFSA-SVM方法建立给水系统故障诊断模型,根据故障状况修改设备可靠性参数,实现了给水系统在线可靠性评价。该方法解决了在机组运行过程中,由于系统设备性能退化或故障而造成的可靠性评价不准确的问题,提高了给水系统可靠性定量计算的准确度。
该可靠性评价方法是整个核电机组的运行状态监控与安全评估的重要组成部分,可推广应用到其他系统的可靠性在线评价。

